基于光电容积脉搏波信号与心电信号相关性的研究*

陈真诚，于邦文，梁永波，曾若生，朱健铭

(1.桂林电子科技大学电子工程与自动化学院，广西 桂林 541004； 2.桂林电子科技大学生命与环境科学学院，广西 桂林 541004)

1 引 言

近年来，我国居民心血管及呼吸类疾病的发病率逐年增长，预防心血管及呼吸类疾病已经成为我国重要的公共卫生安全问题[1]。心电信号(ECG)、容积脉搏波信号(PPG)、呼吸信号(RESP)以及动脉血压信号(ABP)均是研究人体身体健康的重要生理信号。与其余信号相比，PPG信号能够简单、无创地测量人体的生理信息，并且可以连续测量。使用PPG信号进行临床检测具有极大的潜力[2]。

随着技术不断发展，获取人体的各种生理信号已经不是什么难题，但如何通过PPG信号获得与ECG信号、RESP信号以及ABP信号相同的生理信息，是医学家们孜孜以求的目标。因此，我们在研究PPG信号与ECG信号的基础上加入了RESP信号与ABP信号，用于求取各路信号间的相关性指标。目前国内外的研究大多数集中于脉搏波传导时间(PTT)在预测血压(BP)方面的用处[3-4]。有研究表明ECG信号的RR间期与PPG的下降间期具有较高的相关性[5-6]。也有研究探究健康人与患者之间心率变异性的异同[7]。目前为止，并没有研究者探寻PPG信号与RESP信号之间的联系。

目前对信号间相关性的研究多聚焦于PPG间期与ECG间期上[4]，且技术局限于皮尔逊(Pearson)相关系数这一单一指标。而目前为止，偏定向相干性(partial directed coherence，PDC)与定向传递函数(directed transfer function，DTF)在以往的研究中，仍然多用于判断多导联脑电信号之间的因果关系与有向连通性关系[8-9]。

由于PPG与RESP、ECG以及ABP具有相同的激励源(心脏)，在时频域上预期几路信号之间存在相似性是合乎逻辑的。我们主要研究了PPG和ABP、ECG、RESP信号在时域和频域中的关联性，首次将PDC与DTF算法用于判断多路生理信号间的因果关系和有向连通关系，并给出具体的统计学实验结果，为以后使用该类统计学指标做心血管以及呼吸类疾病筛查做准备。

2 数据与处理方法

2.1 数据获取与预处理

本次研究数据来源于麻省理工学院MIMIC II公开数据库。共收集了105组样本，样本采样频率为125 Hz，数据统一时长为60 min。

研究中分别对信号中存在的高噪声，信号缺失，信号削顶等异常信号段做滤波以及排除处理，以使本研究集中于分析不同生理信号间存在的联系。分别用截止频率为0.5～10 Hz，0.5～15 Hz，0.5～40 Hz，0.5～10 Hz的带通滤波器对所有的PPG信号，ABP信号， ECG信号以及RESP信号进行滤波。对于信号记录不良的时间段，如部分数据某一时段无信号等情况，通过目视的方法找到这些记录，并进行信号切割，截取保留剩余滤波后信号。

2.2 同相分析

计算各信号之间的Pearson相关性系数，见式(1)，其中，X代表PPG信号序列，Y分别代表RESP、ECG和ABP信号序列。r的取值范围为[-1,1]，r值越大说明相关性越强，其中越接近1或-1，表明信号之间具有强烈的正相关或负相关关系。

(1)

2.3 异相分析

在频域中进行了三次分析，分别是相干性，PDC以及DTF[10]。这些指标确定的分别是信号之间的耦合关系、直接因果关系及有向连通关系。

(2)

式(2)为相干性的定义。其中，pxx表示信号X的功率谱密度，pyy表示信号Y的功率谱密度，pxy表示信号X,Y的交叉功率谱密度。相干性的取值范围为[0,1]，值越大说明相干性越强，其中越接近1，表明信号之间具有强烈的相干关系。

在以往的研究中，PDC和DTF这些指标主要用于大脑信号之间的因果关系[11-12]。PDC归一化后的结果在[0,1]之间，接近0说明两通道没有联系，大于0.1认为两通道有联系,接近或者等于1说明信号之间存在着非常强的因果关系。PDC算法研究具体如下。

对于多通道自回归AR模型(MVAR模型)，模型可表示为：

(3)

式(3)中，

(4)

本次研究中所处理的信号为四路信号，即m取值为4，在获得四路信号的AR模型后，再对式(3)进行傅里叶变换，得到：

(5)

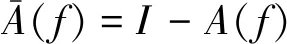
(6)

综上，PDC可定义为：

(7)

DTF在以前的研究[13-14]中有介绍，定义为：

(8)

3 结果

确定PPG与其余三路信号波形形态在对齐时的相关性即为同相分析。表1是同相分析结果，因为样本量以及结果较多，在此不完全列出，仅以PPG信号与ABP信号之间的Pearson相关系数为例。从表中可以看出，105组样本的r值最高为0.9919，其均值r=0.901，标准差SD=0.055，展现出了较强的相关性。表1中Mean表示均值，SD表示标准差，表2中的Mean与SD与此一致。

表1 PPG信号与ABP信号的r值Table 1 Correlation coefficient between PPG signal and ABP signal

表1(续)

个体编号r个体编号r个体编号r个体编号ra44139m0.9812a44496m0.9419a44981m0.9232a45636m0.8331a44164m0.8254a44505m0.8325a44992m0.8947a45641m0.9204a44165m0.9827a44508m0.8238a45045m0.8703a45645m0.8526a44167m0.9265a44526m0.8997a45049m0.9662a45648m0.9308a44171m0.9515a44572m0.9919a45060m0.9171a46098m0.9378a44173m0.9486a44585m0.8681a45098m0.9099a46122m0.9496a44201m0.8784a44590m0.9171a45140m0.9834a46138m0.8901a44215m0.9311a44598m0.8448a45181m0.8572a46176m0.8168a44223m0.8342a44601m0.9503a45186m0.9514a46216m0.8458a44228m0.9412a44615m0.8510a45212m0.9507a46230m0.9827a44233m0.8064a44616m0.9012a45222m0.8761a46289m0.8305a44318m0.8554a44623m0.9398a45227m0.9136a46297m0.9652a44332m0.8092a44626m0.9782a45311m0.8152a46303m0.9077a44347m0.8194a44629m0.9919a45343m0.8108a46416m0.9662a44348m0.9647a44640m0.9094a45353m0.9062a46424m0.9099a44349m0.9390Mean0.901SD0.055

为了更直观地展现表1的结果，特做出相关性系数分布区间图，见图1。从图上可以较为直观地看出所用样本r值的分布情况：横坐标为相关性系数r值，纵坐标为样本量。可以看出相关性r值均分布在[0.8,1]区间，表明了PPG信号与ABP信号之间存在较高的相关性。

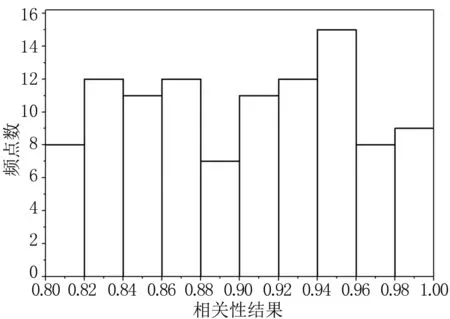
图1 PPG与ABP相关性系数区间分布图Fig.1 Interval distribution of correlation coefficient between PPG and ABP

经过计算发现， PPG与RESP以及ECG之间同样存在非常强的相关性，其相关性系数均值r分别为0.894，0.886。相干性的计算过程与相关性类似，表2为PPG信号与其余三路信号的相关性系数以及相干性系数。MAX表示最大值，MIN表示最小值。R1、R2、 R3分别表示PPG信号与ABP、ECG、RESP信号之间的相关性系数; C1、C2、C3分别表示PPG信号与ABP、ECG、RESP信号之间的相干性系数。图2中R1、R2、R3及C1、C2、C3与此一致。

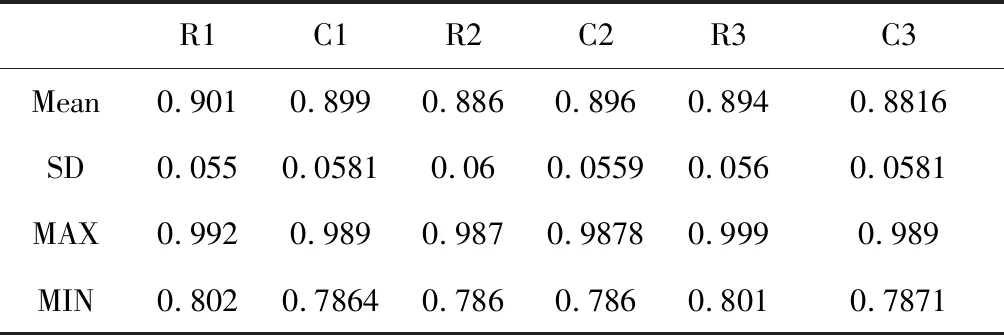
表2 相关性系数及相干性系数Table 2 Correlation coefficient and coherence coefficient

图2为PPG信号与其余三路信号之间相关性系数及相干性系数的箱形图。箱形图可以用来观察数据整体的分布情况，从图中可以较为清晰的看出R1、R2、R3及C1、C2、C3的结果分布情况。

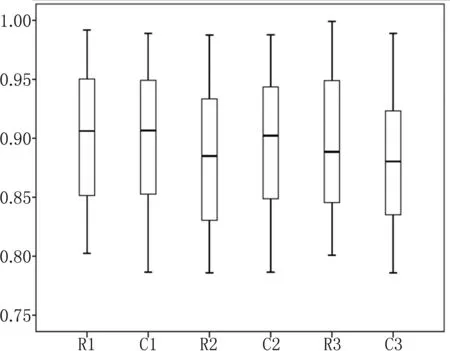
图2 相关性系数及相干性系数箱型图Fig.2 Box type diagram of correlation coefficient and coherence coefficient

有研究表明，ST-PDC在效果上要比其余PDC算法好，因为ST-PDC能准确的跟踪到MVAR模型中快速变化的参数[15],本研究中也采用了ST-PDC以及ST-DTF算法。实验结果见表3。

ST-PDC算法共生成125个矩阵，各矩阵均表示在特定的频率跨度内的PDC结果。表3中CH1、CH2、CH3、CH4分别代表PPG、ABP、RESP、ECG。表中0.9953表示CH1-CH1的PDC结果,即在0～0.24 Hz范围内，PPG信号流向PPG信号的比例占PPG信号流出比例的99%。其余与此类似。ST-PDC算法共产生125个矩阵，在此不全部列出。

图3是基于ST-PDC算法产生的矩阵的折线图，黑色、红色、蓝色、绿色线分别代表着CH1-CH1、CH2-CH1、CH3-CH1以及CH4-CH1的PDC结果。图3所示为个体编号为a44117m的样本数据的125个跨度区间所得PDC值，对应于图4(a)中第一行。对应于105组样本数据，此类折线图共产生125×105个，因为篇幅所限，在此仅列出一列。

表3 特定频率跨度区间PDC结果Table 3 PDC results for specific frequency spans

ST-DTF算法处理过程与ST-PDC类似，在此不再叙述，仅列出最后结果。

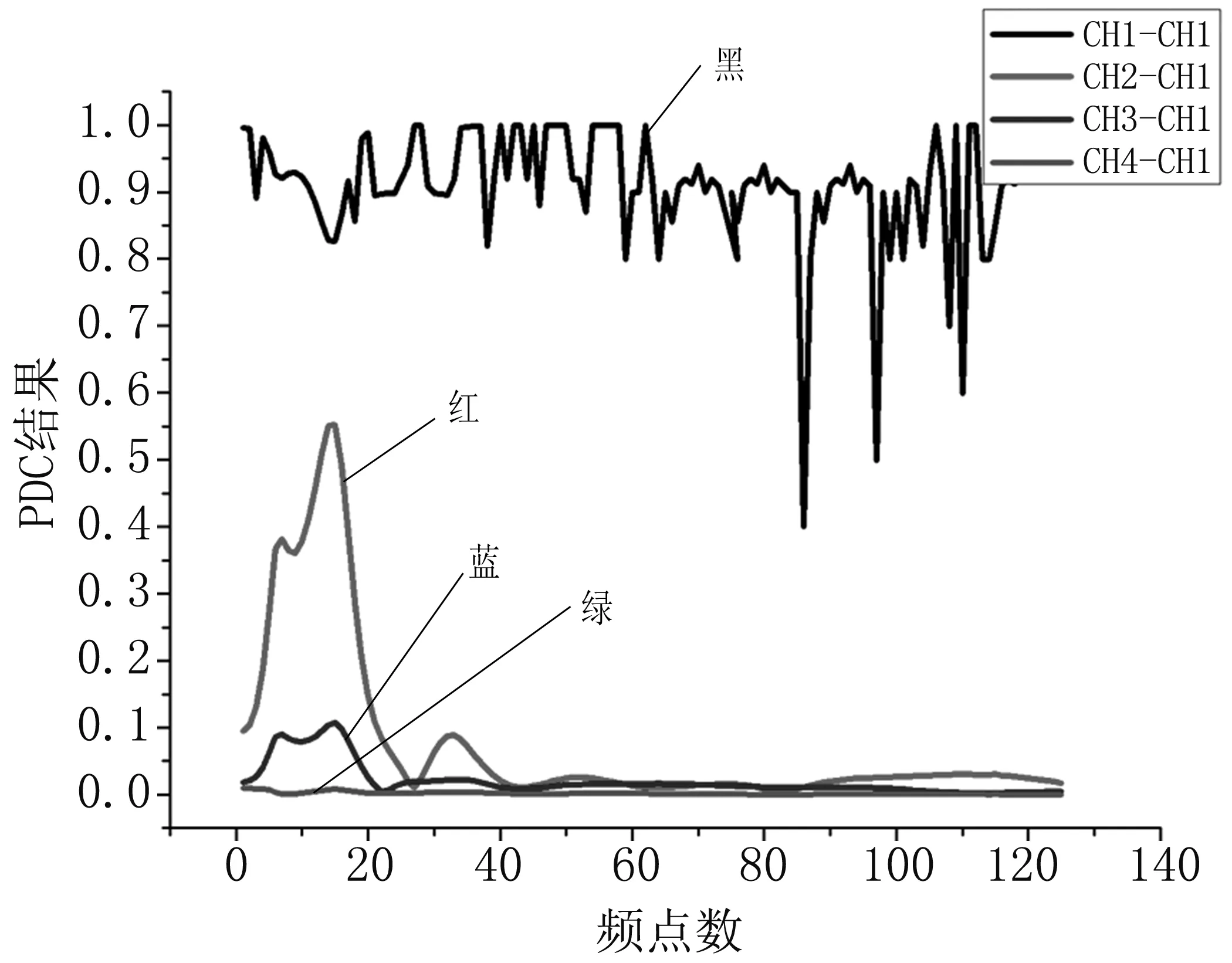
图3 PDC结果折线图Fig.3 Line graph of PDC results

图4(a)表示的是四路信号之间的PDC结果，图4(b)表示的是四路信号的DTF结果。其中，图片中颜色的深浅分别代表着结果的强弱，蓝色表示无相干性或者无连通性。黄色表示因果关系极强。由图4可知，脉搏波信号与其余三路信号无论是在因果关系抑或连通性上均存在较强的关系。

基于图4和表3的结果，可得出图5所示的有向图。

图5是本次研究中PDC与DTF的结果以有向图的形式呈现出来。由图5可知，PPG信号与另外三路信号的异相分析结果也展现出了较强的关系，表明了PPG信号与ABP、RESP以及ECG信号之间存在着较强的因果关系。

在研究生理信号间的PDC与DTF时，从生理学来说，呼吸对血压有显著的影响，呼吸也会影响容积脉搏波信号，心电信号与血压信号间也存在相互的作用，但我们主要探究了PPG→RESP，PPG→ECG, PPG→ABP之间的单向因果流和有向连通性关系，其余暂时不做探究。

(a)

(b)图4 PDC与DTF结果(a).PDC结果;(b).DTF结果Fig.4 The results of PDC and DTF(a).The results of PDC;(b).The results of DTF

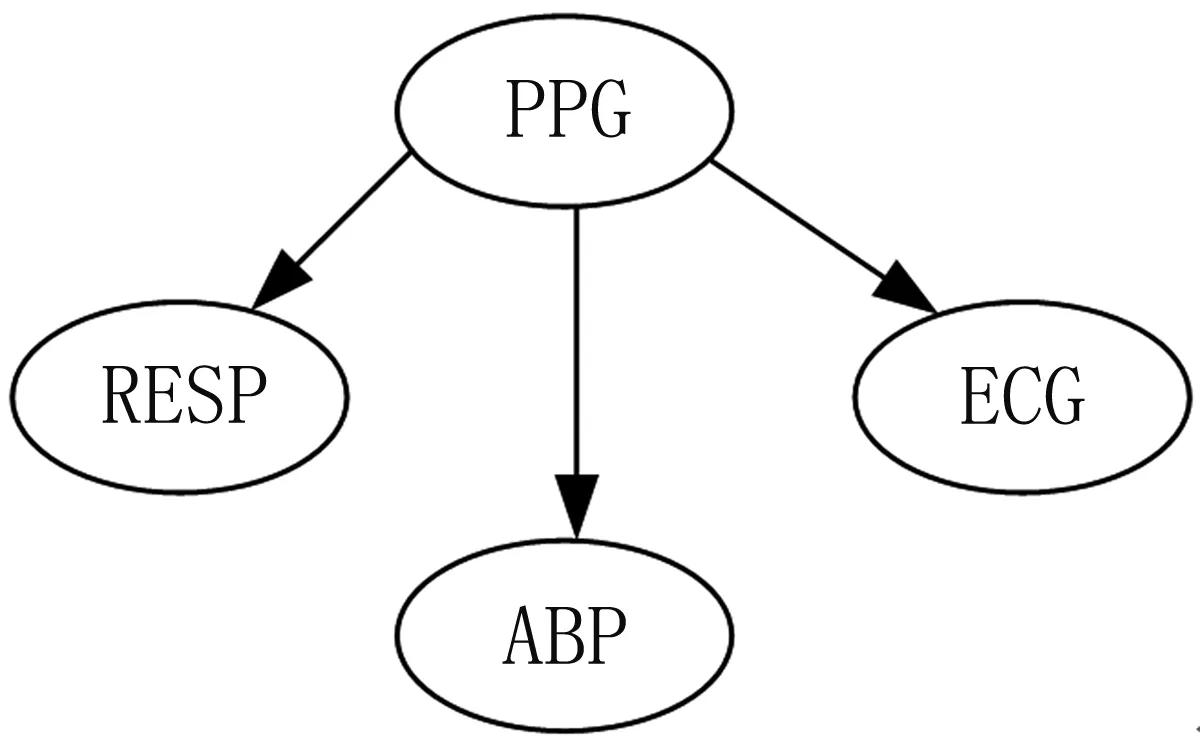
图5 有向图Fig.5 Directed graph

4 讨论

PPG信号受心脏活动，血管壁和外周动脉的影响,是一种非常复杂的生理信号，且生理信息丰富[16-17]。以往对生理信号的研究往往着眼于信号之间的特征点及波形形态上，虽然取得了一定的成就，但存在着处理复杂，精度不够高，手段单一等问题。

近些年有研究表明，利用信号间的统计学指标，如相关性、相干性、偏定性相干性等分类正常血压与高血压是可行的[18]。我们从这些统计学指标入手，验证了四路信号之间的相关性。在本研究中，脉搏波信号与另外三种生理信号的相关性不仅体现在时域的相关系数r的分析上，也体现在频域上的相干性以及PDC与DTF的结果上[15]。实验结果既证实了四路信号在时频域存在的相关性，又提供了可靠的统计学结果，为探索使用信号间的统计学指标进行心血管以及呼吸类疾病筛查奠定了实验基础。

5 结论

本研究结果表明，时域上，PPG信号与ABP、ECG、RESP的相关性均非常高，相关性系数均值分别为0.901、0.894、0.886；频域上，信号间的相干性均值分别为0.899、0.896、0.8816，ST-PDC以及ST-DTF算法结果表明了PPG信号与ABP、ECG、RESP之间同样存在的较强的因果关系。时域与频域的实验结果表明PPG信号与ABP、ECG、RESP信号存在着较强的相关性。

下一步的工作是进一步寻找PPG与ECG、RESP、ABP之间的时频域相关的参数，进而寻找出可判断正常生理信号和非正常生理信号的参数，为判断心血管及呼吸类疾病提供另外一种可靠的途径。