基于时频特征的抹香鲸Click与传统声呐信号的分类方法
卜令冉 华 波 蒋佳佳 颜 晗 段发阶 王宪全 李春月 孙中波
(1.天津大学精密测试技术及仪器国家重点实验室,天津,300072;2.中国船舶工业系统工程研究院,北京,100036)
引 言
声波作为水下最有效的远距离传播载体,在水下通信、水下主动声呐探测、水下无线组网等国防和军事中发挥着至关重要的作用。为了实现通信或主动声呐探测,敌方的水下AUV、UUV、潜艇等都会不时地向水中发射声波信号脉冲,如最常用的单频(Continuous wave,CW)信号、线性调频(Linear frequency modulation,LFM)信号或双曲调频(Hyperbolic frequency modulated,HFM)信号[1]。海洋环境复杂多样,除了通信和主动声呐信号以外,海洋环境中通常还存在许多其他声音,其中,由海洋中鲸类发出的叫声是海洋环境中一类广泛存在的声音。美国[2]、澳大利亚[3]等国家以及欧洲的一些国家[4-5]都建成了较为成熟的海洋被动声学监测网络,对鲸声等海洋哺乳动物声音进行监测研究。
由于鲸的分布广、数量多,鲸类所发出的叫声与主动声呐或通信信号同时出现的概率非常大[6];此外,鲸类所发出叫声的声源级通常非常高,甚至比主动声呐和通信信号的声源级还高。一方面,在对鲸声进行被动声学监测时,如果无法将主动声呐信号和鲸声信号有效区分,则可能会出现监测网络对监测目标误报或者漏报的情况。而目前水下监测网络对水声信号的识别与分类研究,多集中在船舰辐射噪声等低频、持续时间长的噪声[7]或者海洋背景噪声[8]等与目标信号之间的识别与分类,对主动声呐或通信信号的识别与分类研究较少。另一方面,在进行通信或主动声呐探测时,如果无法将强烈和持续的鲸声脉冲信号有效识别与分类,则可能会影响水声通信的可靠性和声呐探测的准确性。而目前主流的水下通信或主动声呐系统几乎都是把海洋哺乳动物所发出的叫声归类为海洋噪声进行处理[9-10]。然而,这些系统多是对接收信号去除海洋背景噪声[10],但鲸声脉冲信号并未被有效滤除,鲸声脉冲信号极易和主动声呐或通信信号混杂在一起,对系统产生干扰,影响系统正常工作。因此,有效识别与分类鲸声脉冲信号与主动声呐或通信信号,对提高水下监测网络、主动声呐和水下通信系统的稳定性和可靠性具有十分重要的作用。
国外一些学者对此做了相关的研究,但这些研究都集中在从海洋噪声(海洋背景噪声或海洋船舶辐射噪声)中提取检测海洋生物脉冲信号。如,Bertilone等[6]提出了一种基于非高斯检测理论和非线性滤波技术的脉冲噪声检测和抑制方法,用于抑制脉冲噪声,在一定程度上提高了主动声呐系统对生物脉冲噪声的抗干扰能力。Ijsselmuide等[10]提出了一种可以应用于低频主动声呐阵列系统的海洋哺乳动物声音的检测方法,基于幂法则(power-law)和Page’s test算法,设计了海豚和鲸鱼等海洋哺乳动物的低频瞬态信号检测器,但方法实现较为复杂。André等[8]对海洋被动声学监测网中鲸和海豚的Click叫声脉冲检测方法进行了研究,并提出了Click叫声脉冲和轮船辐射噪声等人为噪声的检测分类算法。这些研究给出了从海洋噪声中提取检测海洋生物脉冲信号的方法,并取得了良好的检测效果。然而,在海洋生物脉冲信号与主动声呐或通信信号混杂在一起的条件下,正确识别与分类这两类信号,即从混合信号中提取检测海洋生物脉冲信号,同样具有十分重要的意义,但国内外对此领域的研究较少。基于以上分析,本文提出了一种海洋生物脉冲信号与主动声呐或通信信号的识别分类方法。
考虑到绝大多数的鲸和海豚都能发出Click叫声脉冲,且抹香鲸所发出的Click叫声在持续时间长度、频率分布范围、声源级和时频分布等方面都具有一定的代表性,所以本文对抹香鲸所发出的Click以及传统3类具有代表性的声呐信号(CW,LFM,HFM)的分类方法进行了研究,提出了一种基于时频特征的抹香鲸Click与传统声呐信号的分类方法。利用滤波和小波去噪技术对水听器接收到的水声信号进行降噪;通过端点检测方法,提取出4类信号的信号脉冲;对被提取出的信号脉冲进行短时傅里叶变换(Short-time Fourier transform,STFT)计算;并基于STFT时频图,利用所提出的时频轮廓提取方法提取每个脉冲信号对应的时频轮廓图;利用多项式对提取出的时频轮廓图进行曲线拟合,并将多项式的系数作为时频图特征;最后,利用时频图特征训练反向传播(Back propagation,BP)神经网络分类器和支持向量机(Support vector machine,SVM)分类器,并利用被训练的分类器去实现4类信号的分类与识别。
1 时频特征分析
当进行捕食、交流和导航时,抹香鲸会不停地发出Click叫声脉冲。一般地,Click都是宽带脉冲信号,持续时间一般在0.1~30 ms,频率主要分布在100 Hz~30 kHz,且主要能量集中在100 Hz~12 kHz[11]。图1给出了一段抹香鲸叫声的波形图和对应的时频图,可以看出,它们的宽带很宽,且在各个频率内都具有可观的能量。然而传统的声呐信号脉冲(也就是CW,LFM和HFM脉冲)都具有各种独特的特征。进一步地,CW,LFM和HFM信号脉冲的包络均为矩形,CW信号脉冲的频率为单频,LFM信号脉冲的频率呈线性变化,而HFM信号脉冲的频率呈现双曲线形式变化[1,12]。为了直观表示,图2给出了3类传统声呐信号脉冲时频图的一个例子。
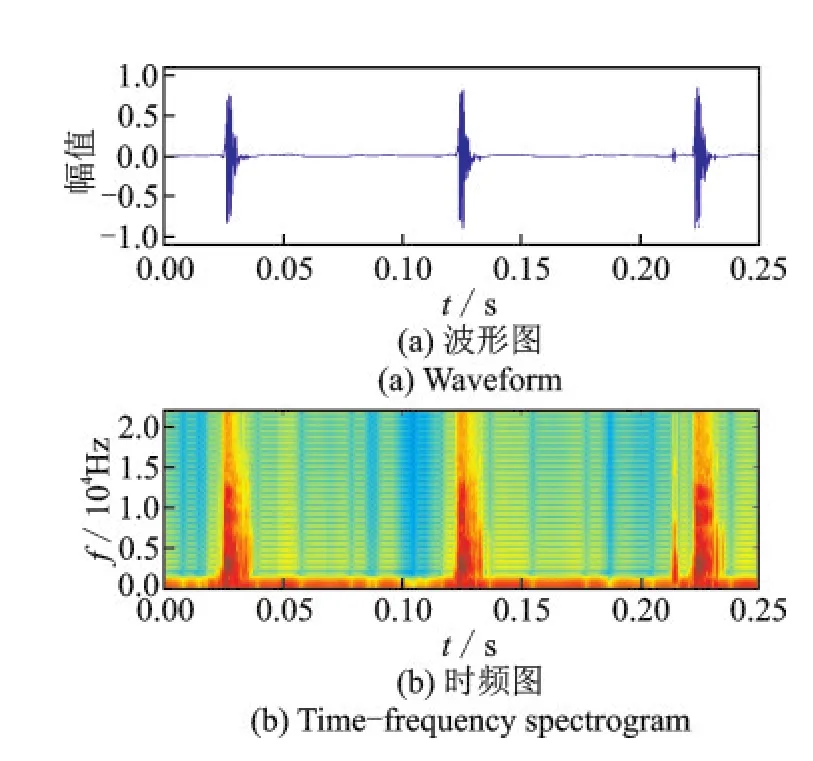
图1 一段抹香鲸叫声的波形图和对应的时频图Fig.1 Waveform and corresponding time-frequency spectrogram ofthe sperm whale sound segment
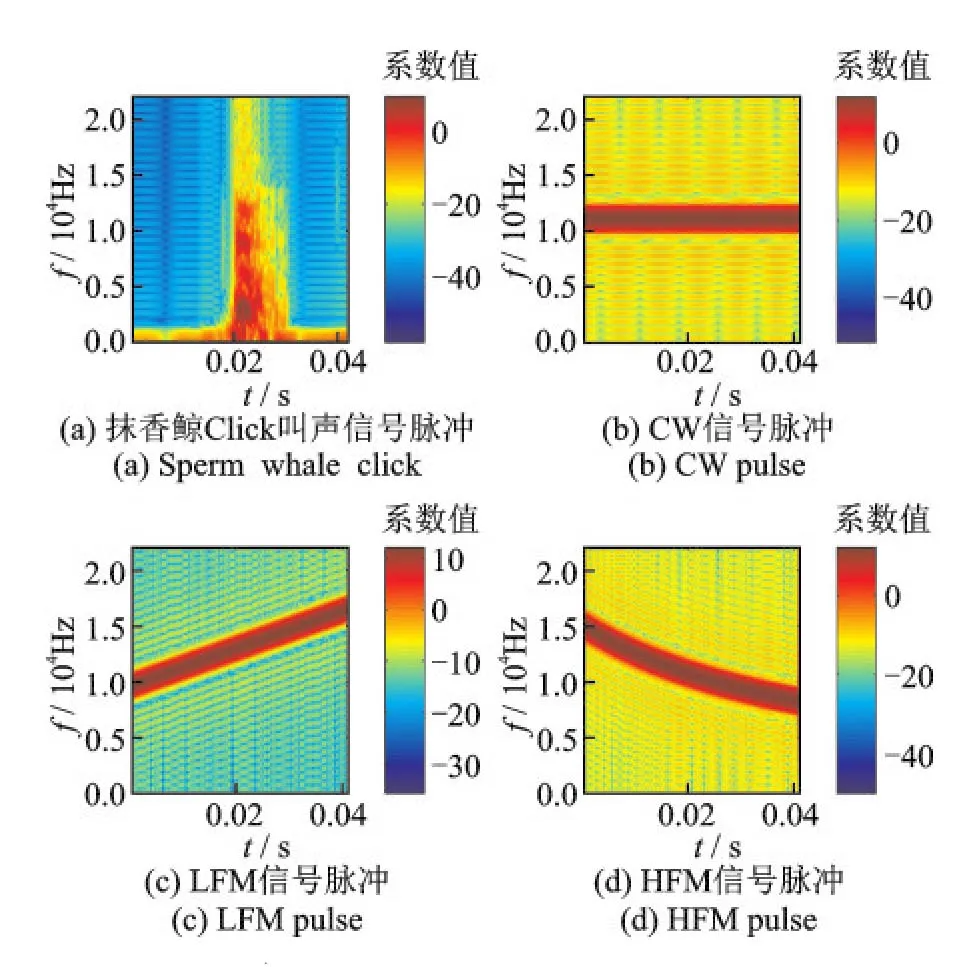
图24类信号脉冲的时频图Fig.2 Time-frequency spectrograms of four signal
2 信号脉冲的时频特征提取与分类
根据上述4类信号脉冲的时频特征分析结果,本文提出了如图3所示的信号脉冲时频特征提取与分类方法:利用滤波和小波去噪技术对水听器接收到的水声信号进行降噪;通过端点检测方法,提取出4类信号的信号脉冲;对被提取出的信号脉冲进行STFT计算;基于STFT时频图,利用所提出的时频轮廓提取方法提取每个脉冲信号对应的时频轮廓图;利用多项式对提取出的时频轮廓图进行曲线拟合,并将多项式的系数作为时频图特征;最后,利用时频图特征训练BP神经网络和SVM,实现4类信号的分类与识别。

图3 信号脉冲时频特征提取与分类方法Fig.3 Signal pulse time-frequency feature extraction and classification method
2.1 去噪和端点检测
鉴于水声信号通常为非平稳信号,首先通过低通和高通滤波器滤除带外噪声,然后,通过小波去噪技术去除叠加在信号中的噪声。由于小波去噪技术很成熟,本文不再详述,具体方法可参见文献[13]。通常情况下,声呐信号和Click均由间隔的脉冲序列组成,因此,在进行STFT之前,首先利用端点检测方法从去噪后的信号序列里提取出所有声呐信号脉冲。其中,端点检测方法可使用传统的语音信号短时能量端点检测算法[14]。
2.2 短时傅里叶变换

式中:x(n)为提取出的脉冲信号;w(n)为窗函数,窗函数的移动距离由m确定;f代表频率。考虑到短时傅里叶变换的时间分辨率和频率分辨率,本文选取汉明(Hamming)窗对信号进行处理,窗宽为60个采样点,步长为10个采样点,FFT点数为1024(信号采样率fs=44.1 kHz)。每一个信号经过短时傅里叶变换,得到相应的短时傅里叶变换谱F(m,f)。按照式(2)对F(m,f)进行对数变换后得到STFT时频图。4类信号时频变换的一个实例见图2。

根据离散时间短时傅里叶变换对提取出的信号脉冲进行变换处理,即
2.3 时频轮廓提取
基于短时傅立叶变换时频图能清晰地反映出信号在不同时刻的频率变化信息,本文提出了一种基于短时傅里叶变换谱的信号时频变化轮廓提取方法。该方法分为以下3个步骤:
(1)对每一个信号的STFT谱F(m,f)取绝对值,得到信号的STFT绝对值矩阵X(m,f),即

(2)对于每一个被窗函数w(n-m)截断的信号切片,都可相应地从X(m,f)中获得当前信号切片内的频谱信息xi(f),即xi(f)=X(mi,f),其中i表示当前信号切片的索引值。求取每个xi(f)在频率f上的最大值mi(f),并计算xi(f)的半功率幅值如图4所示,确定f-xi(f)曲线中mi(f)左右两边的半功率频率点的频率坐标fli和fri,其中fli和fri满足

定义fli和fri的平均值为当前信号切片的瞬时频率fei,fei=1/2×(fli+fri)估计值(图4),则所有切片信号的fei就构成了一个当前信号瞬时频率的序列Fe。

图4 fe的估计原理示意图Fig.4 Schematic diagram of the estimation pri-nciple of fe
(3)对每一个信号的瞬时频率序列Fe,使用移动平均滤波器对其进行平滑滤波,得到平滑信号的时频变化轮廓Se,可根据信号的瞬时频率序列Fe的长度来确定移动平均滤波的长度L。
通过上述方法,便可得到每一个信号的瞬时频率估计值以及时频变化轮廓。图5所示为一个HFM信号的时频谱,通过上述时频轮廓提取方法可提取到图中蓝色线条所示的时频变化轮廓曲线。从图中可以看出,提取出的时频变化轮廓与时频图中能量最大的脊(红色区域)重合,即通过该方法得到的时频变化轮廓可以准确地反映信号的时频变化特征。

图5 HFM信号的时频谱和提取出的时频变化轮廓曲线Fig.5 Time-frequency spectrogram and extracted time-frequency variation contour of HFM signal
2.4 时频曲线拟合与特征提取
基于最小二乘法,使用n阶的多项式p(t)对Ce进行拟合,即

式中:Se(i)表示时频变化轮廓Se中第i个信号切片所对应的值,即平滑滤波后瞬时频率值;ti表示第i个信号切片的中心在原信号中的位;E代表残差。根据最小二乘法,求取式(5)中的系数a0,a1,…,an-1,an,使式(6)表达的残差E达到最小。同时,考虑信号起始段和终止段因频谱泄露等原因而导致Se(i)存在异常值,在处理过程中可根据实际信号的切片个数舍去时频变换轮廓Se左右两端的若干Se(i)值,之后再进行多项式拟合。
上述拟合过程将离散的时频变化轮廓特征转化为连续的时频变化曲线p(t)。图5所示黑色线条为通过上述方法处理后得到的拟合曲线,可以看出,p(t)和信号的时频变化轮廓吻合度非常高。
该信号处理过程将4类信号脉冲的时频图映射成了相应的时频变化拟合曲线p(t),而p(t)的各阶多项式系数a0,a1,…,an-1,an包含了信号的时频变化特征。利用由多项式系数a0,a1,…,an-1,an组成的特征向量A=[a0,a1,…,an-1,an]对分类器进行训练,然后,使用经训练的分类器对4类信号进行分类与识别。
2.5 信号分类与识别
鉴于BP神经网络和SVM都是在目标分类领域被广泛使用的经典分类方法[15],本文分别使用BP神经网络和SVM作为分类器对4类脉冲信号进行分类和识别。
BP神经网络的输入层有n+1个输入层单元,对应输入特征向量中的n+1项多项式系数;输出层有4个输出单元,分别对应Click,CW,LFM和HFM4个信号类别。输入层与隐含层,隐含层与输出层之间使用Log-Sigmoid作为激活函数,输出层到输出结果使用Tan-Sigmoid函数作为激活函数。其中,Tan-Sigmoid函数将输出单元输出限定在(0,1)区间内,输出值大小反映了输入特征可以被分类为当前信号类型的置信程度。通过比较4个输出单元输出值大小,将输入特征分类至其相应的信号类型中。BP神经网络的结构如图6所示,神经网络的详细参数设置如表1所示。

表1 BP神经网络相关参数Tab.1 Related parameters of BP neural network
SVM是一种定义在输入特征空间上的间隔最大分类器,它能较好地解决小样本、非线性、高维数和局部极小点等问题,是求解特征识别分类问题的有效工具。本文使用基于核方法的非线性SVM,通过使用核函数将原空间的分类数据映射到新空间,从而在新空间里用线性分类学习方法从训练数据中学习分类模型。为解决任意维数的特征矩阵问题,选用径向基函数(Radial basis function,RBF)作为核函数。由于SVM一般针对二分类任务,而本文中有4种待分类信号,因此通过“一对一”(one vs one,ovo)方法设计多分类SVM。该方法通过在每两个目标类别之间训练一个分类器来获取分类器的权值和偏置系数;因此对于四分类问题,需要设计6个二分类器。当对输入特征进行分类时,每个分类器都对其类别进行判断,然后在决策阶段采用“投票法”判断输入特征的实际所属类别。所用SVM详细参数如表2所示。

图6 BP神经网络结构示意图Fig.6 Schematic diagram of BP neural network structure

表2 SVM相关参数Tab.2 Related parameters of SVM

式中:Ns为送入两个分类器特征向量的数量,Nc为被两个分类器正确分类的特征向量的数量。
使用分类正确率τ评价以上两个分类器的分类效果,其定义如下
3 实验结果及分析
3.1 实验数据
Click:使用一段通过浮标采集的、时长为7m54s的高质量抹香鲸叫声脉冲信号,信号采样频率为44.1KHz。首先通过高通、低通和小波阈值去噪方法对原始的抹香鲸声音进行去噪,然后,通过基于短时能量的端点检测算法提取出所有Click叫声脉冲,最后从中随机选取800个叫声脉冲用于分类实验。
传统声呐信号脉冲:根据已知的数学表达式,采用软件产生CW,LFM和HFM这3类传统声呐信号脉冲。根据工程实际中低、中、高频声呐所使用的CW,LFM和HFM声呐信号脉冲的频带范围、脉冲宽度等时频参数,通过MATLAB软件随机生成CW,LFM和HFM类信号样本各800个。随机生成的3类信号的时频参数如表3所示,信号的频率范围按照实际使用的低频(1~5 kHz)、中频(5~15 kHz)和高频(15~20 kHz)声呐的频带范围确定。表3中B表示实际生成信号的带宽,在生成信号的过程中,首先确定信号的起始频率,再确定其持续时间,同时根据调频斜率或曲率的参数要求,确定信号的终止频率,最后生成的信号需满足表中所列频率范围,否则生成的信号将被舍去。

表3 CW,LFM和HFM信号参数Tab.3 Signal parameters of CW,LFM and HFM
3.2 实验过程
按照图3所述流程,Click,CW,LFM和HFM水声信号的识别与分类过程如下:
(1)分别对这4类水声信号进行短时傅里叶变换,窗函数取Hamming窗,窗宽为60个采样点,步长为50个采样点,FFT长度为1024。
(2)在估计每个实验信号样本的时频变化轮廓Se时,移动平均滤波的长度设置为L=10。
(3)设置拟合多项式阶数n=5。为减小时频变化轮廓异常值对拟合精度的影响,仅使用Se中间4/5的长度进行拟合(将左右两端各1/10长度的Se(i)舍去),得到时频变化特征向量A=[a0,a1,…,an-1,an]。
(4)使用k-折交叉验证法评估BP神经网络和SVM的分类性能。具体过程如下:首先,将每一类水声信号中的800个特征向量随机切分为10个互不相交且大小相同的子集(即k=10),使每一个子集都包含80个数据样本。然后,每一次使用4类水声信号中的9个子集的并集作为BP神经网络和SVM的训练集(即4×9×80共2880个训练样本),余下的4类水声信号子集的并集作为BP神经网络和SVM的测试集(即4×(10-9)×80共320个特征向量样本)。进行10次训练和测试,保证每个子集都有一次机会作为测试集,其余作为训练集。用训练好的模型在相应的测试集上测试,计算并保存模型的评估结果。最后,将10组测试集上分类正确率的平均值作为分类器的分类成功概率。
3.3 忽略水声信道影响下的分类结果
表4和表5分别列出了BP神经网络交叉验证实验和SVM交叉验证实验混淆矩阵(Confusion matrix)的平均值和平均分类正确率。对比表4和表5的结果,可以发现在相同训练集和测试集条件下,BP神经网络对Click,LFM和HFM信号的识别和分类能力优于SVM,两者的CW分类正确率相差不大,但SVM对LFM和HFM的分类能力较差,分类正确率远低于BP神经网络。BP神经网络对4类信号的分类正确率均高于90%。

表4 BP神经网络分类结果Tab.4 Classification results of BP neural network
从表5还可以看出,SVM对LFM和HFM分类准确率较低,主要表现在SVM将较多的LFM测试样本(30.75%)错误地分类到HFM,同时也将较多的HFM测试样本(32%)错误地分类到LFM。这表明,相比其他两类信号,LFM和HFM的时频变化趋势更为相似,两者时频特征向量在SVM的输入特征空间有较多重合区域,同时SVM的核函数无法将两者的时频特征向量有效映射到线性可分空间内,最终导致SVM将较多的LFM和HFM特征向量错误分类。
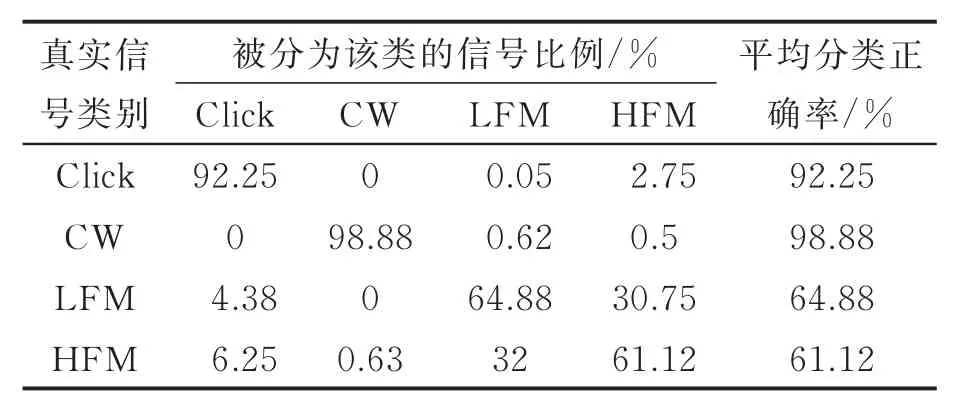
表5 SVM分类结果Tab.5 Classification results of SVM
3.4 水声信道影响下的分类结果
在水声信号实际传播过程中,受海洋水声信道频率选择性、时变、多途效应等的影响,4类信号在传播过程中会产生不同程度的信号畸变[16],但在3.3节中这一现象未被考虑在内。因此使用Bellhop模型对海洋声信道传播特性进行建模仿真,获取信道冲激响应[17],考察在水声信道影响下4类信号的分类效果。Bellhop模型建模仿真参数如表6所示。

表6 Bellhop模型仿真参数Tab.6 Simulation parameters of the Bellhop model
对3200个经过水声信道后的接收信号按照图3所述实验过程再次进行实验。表7和表8分别列出了BP神经网络和SVM分类器混淆矩阵的平均值和平均分类正确率。从表中看出,BP神经网络和SVM对Click和CW的分类效果没有大幅变化,但对LFM和HFM的分类效果明显下降。BP神经网络几乎是对经水声信道后的LFM和HFM信号进行了随机分类。这主要是由于受信道影响后,LFM和HFM信号出现严重的时间扩展,产生了锯齿状的信号重叠现象,影响时频特征提取算法对信号瞬时频率的估计,导致算法无法准确提取原信号时频脊的斜率或曲率细节变化等特征,但这种影响仅体现在这两类信号之间。除此之外,BP神经网络仍能准确分类Click和CW信号,平均分类正确率分别达到96.88%和92.65%。这是由于同LFM和HFM信号相比,Click和CW信号频率变化更平稳,信道对其时频变化影响较小。
SVM相比BP神经网络分类效果较差。和原始信号分类结果相比,SVM对4类信号的分类正确率均有所下降。SVM除不能准确分类经水声信道后的LFM和HFM信号外,还将28.38%的LFM信号和31.38%的HFM信号错误分类为Click信号,这同样说明三者的时频特征在SVM的输入特征空间存在重合区域且核函数不能将三者正确映射到线性可分空间。

表7 BP神经网络对经水声信道后信号的分类结果Tab.7 Classification results of BP neural network on signals after the simulated underwater acoustic channel

表8 SVM对经水声信道后信号的分类结果Tab.8 Classification results of SVM on signals after the simulated underwater acoustic channel
3.5 水声信道影响被补偿后的分类结果
在本部分,通过虚拟时间反转镜技术对水声信道的影响进行了补偿[16]。经过虚拟时间反转镜补偿后的4类水声信号按照图3所述实验过程再次进行实验。其中,在估计每一个实验信号样本时频变化轮廓Se过程中,由于信号在时间上被压缩聚焦,左右两端信号幅值明显减小,为减小两端低幅值信号对拟合效果的影响,将低于信号最大幅值1/5的两端信号对应的Se(i)值舍去,只保留中间时间段内对应幅值较大的Se(i)进行时频曲线拟合。表9和表10分别列出了BP神经网络和SVM分类器混淆矩阵的平均值和平均分类正确率。
和补偿前相比,BP神经网络对补偿后的Click,CW,LFM和HFM信号的平均分类正确率分别达到95.5%,94.25%,82.87%和86%,其中对LFM和HFM信号的分类正确率分别提高了38.9%和43.9%,分类效果明显改善。SVM对于补偿后Click,CW,LFM和HFM信号的分类效果仍然比较差,平均分类正确率分别为85.75%,92.38%,37.9%和44.75%,和未补偿信号的分类正确率相当,均低于BP神经网络分类正确率。从混淆矩阵看,和补偿前相比,SVM将补偿后LFM和HFM信号错误分类到Click的比例明显减少,LFM错分到Click的比例由原来的28.38%下降到16.25%,HFM错分到Click的比例由原来的31.38%下降到11.38%。
对比3组实验结果可以发现,BP神经网络比SVM分类器具有更好的适应性和分类效果。

表9 BP神经网络对水声信道补偿后信号的分类结果Tab.9 Classification results of BP neural network after compensation for underwater acoustic channel

表10 SVM对水声信道补偿后信号的分类结果Tab.10 Classification results of SVM after compensation for underwater acoustic channel
4 结束语
本文提出了一种基于短时傅里叶变换的Click,CW,LFM和HFM水声信号时频特征提取和分类算法。本算法基于短时傅里叶变换谱,对信号瞬时频率进行估计,进而提取信号的时频变化轮廓,通过对时频变化轮廓进行多项式拟合,将离散的时频变化轮廓转化为连续的时频特征曲线,最终计算得到时频特征向量。进一步地,基于特征向量,利用BP神经网络和SVM分类器对4类信号进行分类。分别在理想情况下、在水声信道对信号产生影响的情况下和在水声信道的影响被校正的情况下,进行了分类实验。实验结果表明,所提出的时频特征识别分类算法可以准确提取4类水声信号的时频变化特征并将其正确分类。BP神经网络分类器比SVM分类具有更好的适应性和分类正确率。从实验结果可以看出,在3种实验条件下,仅使用小规模数据(每一类信号800个数据样本)对BP神经网络进行训练即可使分类器对Click信号的分类正确率达到95%以上。本文提出的时频特征分类和识别算法模型结构简单,运算量小,可搭载于小型或微型嵌入式系统,可应用在被动声学监测、主动声呐探测以及水声通信等场景下的多类信号的分类与识别,以及水下军事预警等领域。

