密度空间与密度峰值聚类的欠定混合矩阵估计
何选森 何 帆
(1.广州商学院信息技术与工程学院,广州,511363;2.湖南大学信息科学与工程学院,长沙,410082;3.北京理工大学管理与经济学院,北京,100081)
引 言
在信源和传输信道均未知的情况下,仅利用传感器采集获得的观测信号来分离信源的过程称为盲源分离(Blind source separation,BSS)[1]。在无噪情况下,BSS的时域模型为:x(t)=As(t),其中s(t)=[s1(t),s2(t),…,sM(t)]T为源信号向量,x(t)=[x1(t),x2(t),…,xN(t)]T为观测信号向量,A∈RN×M为混合矩阵。当M=N,称BSS为适定的;若M<N则称BSS为超定的;若M>N,则称为欠定的盲源分离(Underdetermined BSS,UBSS)[1]。在UBSS问题中,由于混合矩阵的逆不存在,对它的估计是很困难的[2],且辨识混合矩阵与分离信源成为两个截然不同的问题。因此,两步法[3]成为UBSS的主要解决方案,其中第一步是估计混合矩阵,第二步是分离源信号。而至关重要的是对混合矩阵的估计,因为它的结果直接影响到BSS的性能。
近些年,利用群体智能算法解决UBSS问题成为国内外学者的研究热点,主要包括蚁群优化算法[4],人工蜂群算法[5],粒子群算法[6]等;而对于单通道的UBSS,基于粒子滤波[7]以及粒子流滤波[8]的方法在改进UBSS性能方面也取得了一定的进展。另外,充分利用自然信号(如音频,图像等)本身具有的稀疏特性来解决UBSS问题已成为业界的共识。因此,稀疏表示[9]和稀疏分量分析[10]是处理UBSS问题最基础和最有效的方法。由于稀疏信号具有线性聚类特性,且聚类形成的直线方向向量就是混合矩阵的列向量[11],因此对观测信号进行聚类分析能实现混合矩阵的估计。常用的聚类方法有K-均值[12],霍夫变换[13],势函数[3]等。另外,把两种不同聚类方法组合能形成更有效的聚类分析。例如:算法KHough[14]利用霍夫变换对K-均值的聚类中心进行修正,同时K-Hough还克服了霍夫变换在进行峰值提取时的峰值簇拥问题;DBSCAN-Hough[15]采用具有噪声的基于密度空间聚类(Density based spatial clustering of applications with noise,DBSCAN)算法[16]确定聚类的数目,通过霍夫变换对聚类中心进一步修正。正是从这些组合的方法中得到启发,本文利用单源点(Single-source-point,SSP)检测以增加信源的线性聚类特性,然后把DBSCAN算法和快速搜索与寻找密度峰值聚类(clustering by fast search and find of density peaks,CFSFDP)算法[17]相结合形成新的聚类分析方法。选择DBSCAN是因为它能对观测数据进行聚类以自动确定信源数目,从而克服了K-均值算法需事先预知信源数目的缺陷。然而,DBSCAN算法对于高维数信号,或密度不均匀、聚类间距相差很大的信源,其聚类效果不理想。为此,在DBSCAN聚类分析的基础上,利用CFSFDP对每一类数据分别计算出对应的密度峰值,并把峰值点作为修正后的聚类中心,从而提高混合矩阵的估计精度。把DBSCAN和CFSFDP两种聚类算法相结合的另一个优势是DBSCAN能弥补CFSFDP算法需要人为干预的不足。
1 单源点检测
对于时域BSS模型x(t)=As(t),两边取短时傅里叶变换(Short-time Fourier transform,STFT),则
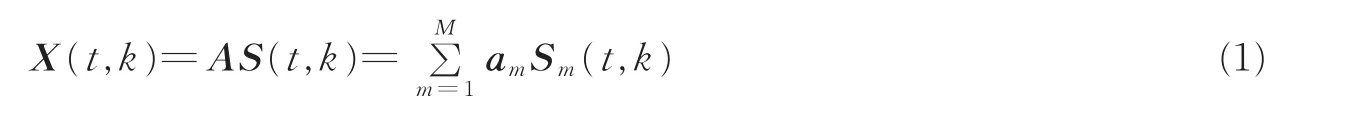
式中:X(t,k)=[X1(t,k),X2(t,k),…,XN(t,k)]T和S(t,k)=[S1(t,k),S2(t,k),…,SM(t,k)]T分别为x(t)∈RN和s(t)∈RM在时频点(t,k)的STFT的系数;am为混合矩阵A的第m个列向量。与时域相比,时频域中稀疏信号的直线聚类特性得到了更好的体现,但仍存在有一些观测数据不能聚集在直线上,而是处于直线之外,这就造成混合矩阵的估计性能下降。为此,本文采用SSP检测[18]。所谓SSP是指在这些时频点上只有一个主导信源的能量具有较大的值,而其余信源能量很小以至于可忽略。而不满足SSP条件的时频点称为多源点(Multi-source-points,MSP)。显然,SSP检测后的数据具有显著直线聚类的方向性。
对于任意一个时频点(t,k),观测信号X(t,k)的实部和虚部分别为
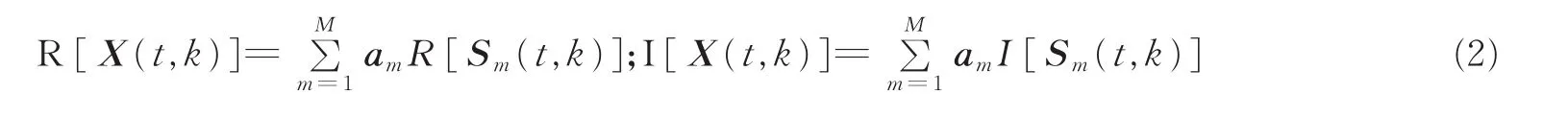
这二者之间的夹角θ为
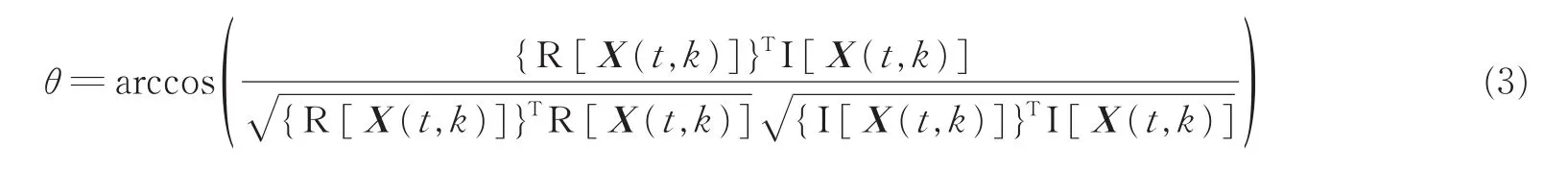
如果信源各分量的实部与虚部之比是相等的,即满足以下关系
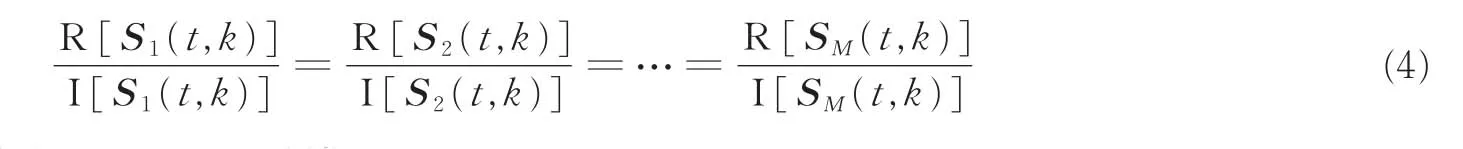
则它们之间的夹角θ=0°或θ=π(180°)。这时,就称该时频点(t,k)是 SSP。
在实际应用中,恒等式(4)成立的条件是很苛刻的。为此可采用另一个判断条件[18]:若R[X(t,k)]和I[X(t,k)]的绝对方向相同,则对应的时频点(t,k)就称为SSP。通常情况下,若R[X(t,k)]和I[X(t,k)]的绝对方向夹角小于某个阈值Δθ时,就认为时频点(t,k)是SSP,即
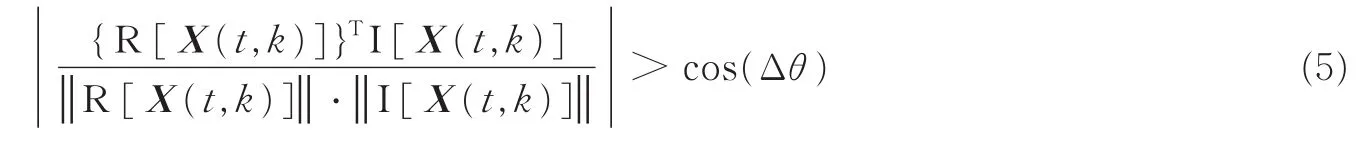
式中:|z|表示z的绝对值,而||Z||=(ZTZ)1/2。本文采用的阈值为Δθ=0.8°。
通过SSP检测之后,由于剔除了MSP,则观测信号的数据分布凸显出了明确的方向性。由所有SSP的数据点组成的集合记为Xssp。
一般地,经过原点的直线方向可以被两个方向相反的向量来表示。例如,在三维空间中同一条直线可被方向向量(1,1,1)或(-1,-1,-1)来描述。为了用唯一的方向向量描述直线,采用镜像映射[4]方式,将负方向的向量映射到对应的正方向上。在信号处理领域,利用观测信号的归一化可实现镜像映射的过程[11]

从式(6)可知,镜像映射是把线性聚类转换成致密聚类,便于利用基于密度聚类方法搜索到密集数据堆中的关键数据点(聚类中心)。该数据点的方向就是稀疏信号线性聚类的直线方向,即混合矩阵的列向量。因此,通过对数据X*(k)进行聚类分析就可实现对欠定混合矩阵的估计。
2 聚类分析
在众多聚类方法中,DBSCAN作为基于密度聚类的典型代表,能够在有噪声的数据中发现各种形状和各种大小的数据簇。DBSCAN的核心思想是在数据堆中找到密度较高的数据点,再通过搜索邻近的其他高密度数据点,逐步将高密度数据点连成一片,从而生成各种形状的数据簇。
DBSCAN算法是利用参数(eps,MinPts)来描述邻域的样本分布紧密程度。首先,以每个数据点为圆心,以邻域eps为半径画个圆圈,落在该圈内的数据点数就是该点的密度值。然后,利用密度阈值MinPts判断数据点的密度级别,若圆圈内数据点数小于MinPts,则其圆心的数据点是低密度点,而点数大于或等于MinPts的圆心数据点为高密度点(核心点Core point)。若某个低密度数据点落在高密度点的圆圈内,则把低密度点连到最邻近的高密度点上,并称它为高密度点的边界点。不在任何高密度点圈内的低密度点为异常点(噪声)。
若某个样本点y在点x的eps邻域内,且x为核心点,则称y从x直接密度可达。假设给定一连串数据样本点x1,x2,…,xn且x=x1,y=xn,若xi+1从xi(i∈[1,n])直接密度可达,则称y从x密度可达。对于样本点xi和xj,若存在核心点xk,使xi和xj都可以由xk密度可达,则称样本点xi和xj密度相连。由密度可达关系得到的最大密度相连的样本集合,即为聚类分析最终得到的一个类别(簇)。
DBSCAN的聚类效果取决于参数eps和MinPts的选取。MinPts的选取原则是:MinPts≥D+1,其中D为待聚类数据的维度;一般地,MinPts必须选择大于等于3的值。参数eps的选择也要适中:若eps值太小,会造成大部分数据不能聚类;若eps值过大,会使多个数据簇被合并到同一个簇中。eps选择可通过绘制K-距离曲线来实现,在曲线的明显拐点位置对应于合适的eps参数值。
与传统的K-均值聚类相比,DBSCAN算法的优势主要体现在:(1)可以对任意形状的稠密数据集进行聚类,而K-均值仅适用于凸数据集;(2)可以自动获得聚类的数量,而K-均值需事先给定聚类数;(3)在聚类的同时还能找出异常(噪声)点;(4)聚类的结果没有偏移,而K-均值的初始值对聚类结果影响很大。
然而,由于使用全局的密度阈值参数MinPts,DBSCAN只能发现密度值不少于MinPts的数据点所组成的簇,而很难发现不同密度的数据簇。为此,本文采用可视化的CFSFDP算法对DBSCAN产生的初步聚类中心进行修正,以提高关键数据的定位精度。CFSFDP的基本思想是:由于每个数据簇都有一个最大密度的数据点作为簇中心,在它的周围都是密度比它低的数据点;使得不同的数据簇的中心相距较远,从而可区分出不同密度的数据簇。显然,CFSFDP弥补了DBSCAN算法仅适合于稠密数据集的缺陷。
假设观测数据集为X={xi|i=1,2,…,n},数据点xi和xj之间距离为dij=dist(xi,xj),该距离可以采用欧氏距离、马氏距离、汉明距离和曼哈顿距离等。对于数据集X中的任何点xi,定义它的两个基本属性:局部密度ρi以及它与最近的高密度数据点的距离δi。ρi的计算方式有两种:Cut-off kernel和Gaussian kernel,其中Cut-off kernel方式的计算公式为[17]

而χ函数定义为

参数dc>0为截断距离,需要用户提前设置,且CFSFDP算法对截断距离不敏感。由定义式(7)可以看出,局部密度ρi是数据集X中与xi之间距离小于dc的数据点的个数。
局部密度ρi的Gaussian kernel方式的计算式为[17]

比较定义式(7)和式(9)可知,Cut-off kernel方式的计算结果为离散值,Gaussian kernel方式的计算结果为连续值。因此,在Gaussian kernel的结果中,发生不同数据点具有相同局部密度值的概率会更小。
设qi(i=1,2,…,n)是ρi(i=1,2,…,n)的一个降序排列的序列,即ρq1≥ρq2
≥ρq3
≥ … ≥ρqn,则点qi与高密度数据点的距离定义为[17]

显然,δi表示数据集X中任一点xi和所有局部密度大于它密度的点之间的最小距离;当xi的局部密度是最大时,δi是其他所有聚类中最大的一个。局部密度最大的点一定也是一个数据簇的聚类中心。
对数据集X中每个点xi,计算出二元对(ρi,δi),以ρi为横坐标,δi为纵坐标画出(ρi,δi)的决策图,在该图中,同时具有较大ρi和δi值的数据点会脱颖而出,这些点就可以看作是聚类中心;而ρi值很小且δi值很大的数据点就是离群点。显然,利用决策图确定聚类中心属于定性分析而非定量分析,需要人为干预。为了减少人为因素的影响,定义一个综合考虑ρi与δi值的量

ξi的值越大,则所对应的数据点xi越有可能是聚类中心。
CFSFDP算法中截断距离dc的确定方法如下。分配给每个点的平均邻居数量约为数据点总数的1%~2%,所谓邻居就是指某点在dc距离范围内的数据点。对数据集X中每个点,它与其他的n-1个点都有一个距离,总共有n(n-1)个距离。因为每个点对应的距离都被计算了两次,因此这些距离有一半是重复的。为此,把距离dij(i<j)按升序排列为d1≤d2≤…≤dM。若取dc=dk(k=1,2,…,M),则在所有n(n-1)个距离中,小于dc的距离所占的比例约为t=k/M,即大约有(k/M)n(n-1)个距离小于dc。比值t就是选取参数dc的重要指标。
参数dc值的选取决定着CFSFDP的聚类效果。若dc值过大,会使每个数据点的ρi值都很大,导致聚类的区分度不高;在极端情况下dc=dM,则所有的数据点都归属于一个簇。若dc值太小,同一聚类中就可能被拆分成多个簇;在极端的情况下dc<d1,则每一个数据点都单独成为一个簇。选取dc值是依赖于具体问题的。通过采取比例值t来确定参数dc的策略,可降低对具体问题的依赖性。
从以上分析可知,DBSCAN是单独以密度为指标选择聚类的类别,而CFSFDP综合考虑了密度和距离两个指标作为选择聚类的类别。因此,CFSFDP能够区分出两个密度值很接近的不同的两个聚类。在利用聚类分析估计混合矩阵过程中,本文首先把计算得到的ξi(i=1,2,…,n)值按降序排列,然后从大到小截取由算法DBSCAN得到聚类中心数量相对应的ξi值的数据点作为聚类中心。这意味着,把DBSCAN获得的聚类数量作为CFSFDP的输入参数,通过CFSFDP进一步搜索密度峰值以修正DBSCAN的聚类中心位置;同时DBSCAN也弥补了CFSFDP需要人为干预的不足,使两种算法扬长补短,得到最佳的组合。
本文方法的基本流程如图1所示。

图1 本文提出方法的基本流程图Fig.1 Basic flow chart of the proposed method
在利用聚类方法获得混合矩阵的估计之后,采用最短路径方法[3]就可以容易地分离(恢复)出信源。
3 仿真结果与分析
为了验证本文方法的有效性,在混合矩阵估计和信源分离两个方面进行仿真测试。特别地,把K-means算法[11,12]、基于层次的聚类(Hierarchical clustering,HC)算法[19]与本文算法在混合矩阵估计的性能方面进行比较。仿真测试中,为了获得尽可能公平的结果,所有算法的仿真环境都是同样的。
3.1 仿真环境与性能指标
仿真的PC平台:Intel(R)Celeron(R)1007U-1.5 GHz的CPU,4 GB内存,操作系统Windows 10,所有仿真都是运行在MATLAB 9(R2016a)上。用于测试的信源为SixFlutes数据集[3]中的长笛演奏音乐信号,其采样率为44.1 kHz,信号样本长度为216=65536。源信号向量记作s(t)=[s1(t),s2(t),s3(t),s4(t),s5(t),s6(t)]T,6路信源的时域波形如图2所示。
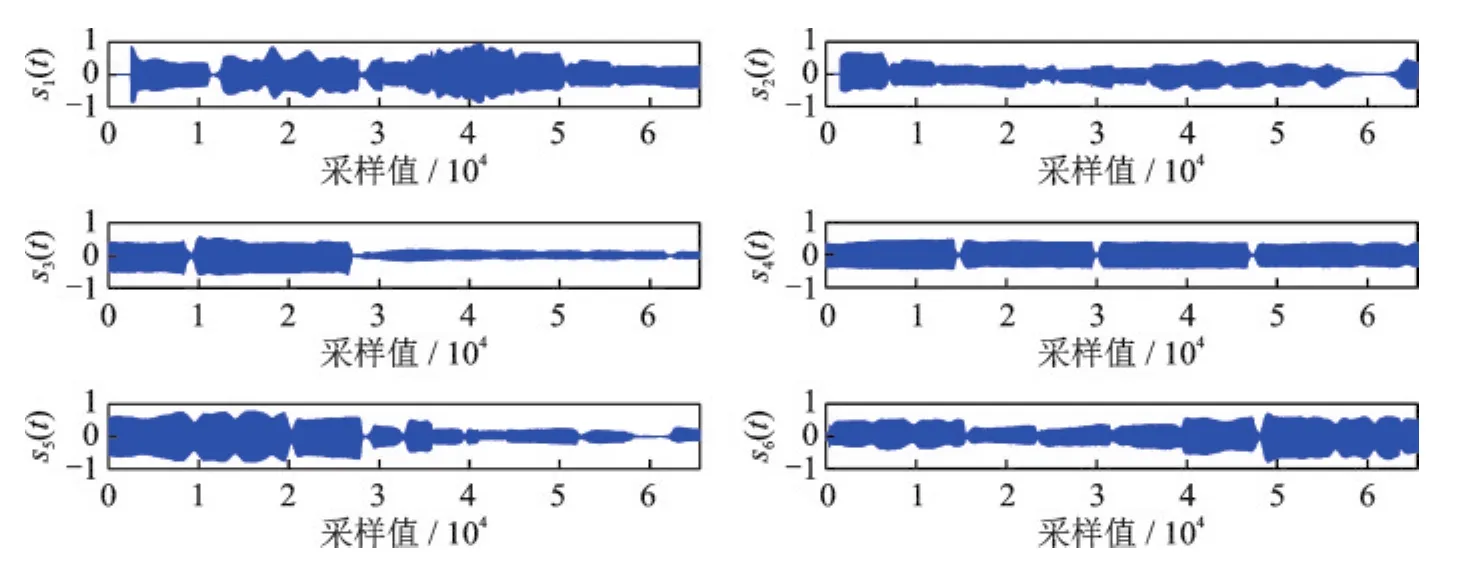
图26路音乐源信号的时域波形Fig.2 Time domain waveforms of six music source signals
为了测试算法对混合矩阵的估计精度,采用角度偏差[11]作为技术指标
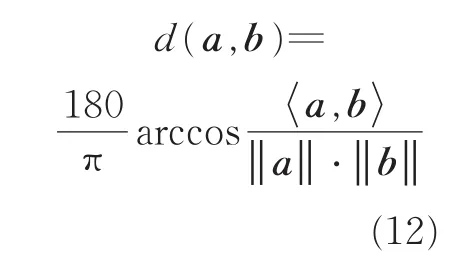
式中:a为原始混合矩阵A的列向量,b为估计出混合矩阵B的列向量,〈a,b〉表示向量a与b的内积。如果角度偏差d(a,b)的值越小,说明混合矩阵的估计精度越高。另外,采用均方误差(Mean square error,MSE)作为测度混合矩阵估计的另一个技术指标,表达式为
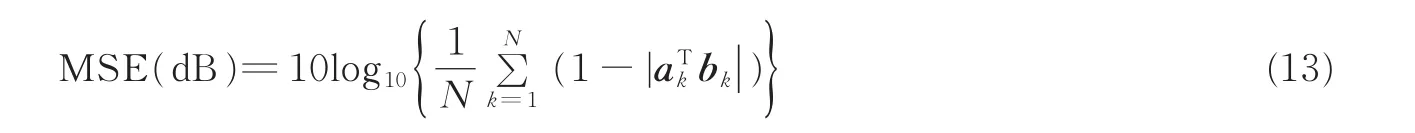
式中:ak为原始混合矩阵A的第k个列向量,bk为估计出混合矩阵B的第k个列向量,ak和bk都是归一化的向量。ak和bk的方向越接近,其|akTbk|的值越接近于1,说明混合矩阵估计精度越高。
在混合矩阵被估计出来之后,利用最短路径法即可分离(恢复)源信号。为了度量原始的信源与估计的信源之间的相似性,采用相关系数[11]作为性能指标,表达式为
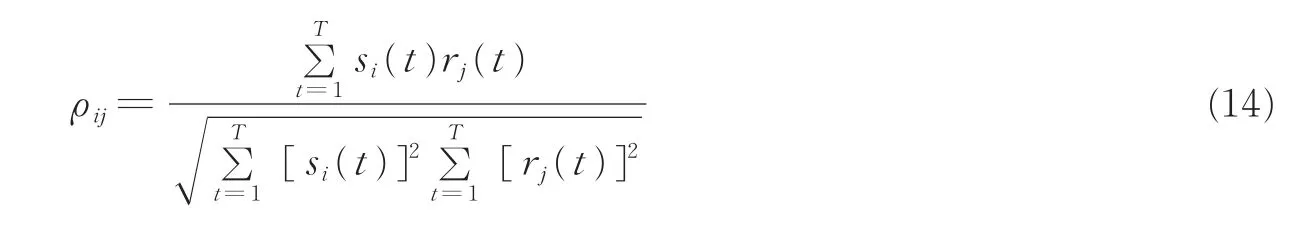
式中:si(t)为时域中第i个信源,rj(t)为时域中第j个恢复的信源,T为时域中信号的样本数。如果恢复的信源与原始的信源越相似,其相关系数ρii就越接近于1或-1,而ρij(i≠j)越接近于0。
在下面的仿真中,首先在时域中把6个信源随机地混合成3路观测信号;然后利用STFT把时域信号变换到时频域中进行混合矩阵的估计,在进行STFT操作时,利用Hanning窗截断来实现对信号的分帧,每一帧的长度为L=8192,两个连续帧的重叠率为60%;最后将恢复出的源信号通过逆STFT再变换到时域中,在时域中进行相关系数的计算。这里对STFT的参数选择说明如下。对于音频信号的处理,一般来说是需要进行分帧的;为了避免信号所含信息的损失,要求连续两帧之间的样本要重叠。由于每个信号的样本长度为65536,要将信号分成整数帧(一般为2的整数次幂,本文取23=8),则可得每帧长度为L=65536/8=8192。对于连续两帧之间重叠的样本数,在实际应用中,一般取d=round(0.15×L×4),其中round(x)为对数据x取整操作[11]。这样就可得到重叠的样本数为d=round(0.6×L)=4915,即连续两帧的重叠率为60%。利用窗函数截断来实现音频信号的分帧则是信号处理最重用的方法,在文献[11]中对Barlett,Blackman,Flot top,Hanning,Hamming,Kaiser,Tukey,Welh,Boxcar等常见的窗函数的特点及适用的信号类型进行了详细的分析。Hanning窗函数能够在较好幅度精度的情况下,提供良好的频率分辨率和泄露保护[11];另外,在对音频信号处理中,Hanning窗还具有非常低的频率混叠的优势[11]。因此,本文采用Hanning窗实现对音频信号的分帧处理。
3.2 结果及分析
仿真中,混合矩阵是利用MATLAB命令A=rand(3,6)随机产生,即

3路观测信号x(t)=[x1(t),x2(t),x3(t)]T=As(t)是由6个信源s(t)混合而成。x(t)的时域波形如图3所示。
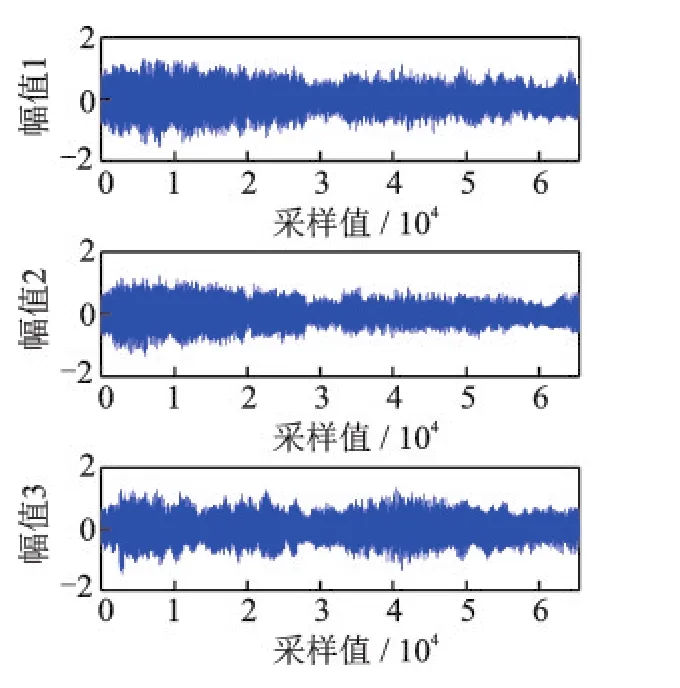
图33路观测信号的时域波形Fig.3 Time domain waveforms of three observed signals
图4给出了x(t)的时域散点图。所谓散点图是指信号的数据点在直角坐标系上的分布图,其表示的是因变量随自变量而变化的大致趋势。从图4可知,由于时域的数据点密集地分布在一起,没有显示出稀疏信号的线性聚类特性,因而无法分辨信源的数量和方向。为此,需要对时域信号x(t)进行STFT,得到时频域中的观测信号X(t,k)=[X1(t,k),X2(t,k),X3(t,k)]T。在时频域中信号X(t,k)的散点图如图5所示。
从图5可以看出,时频域中稀疏信号的线性聚类特性得到了明显的增强。但在几条由数据点组成的直线之间仍然分布着很多数据
点,这就造成了线性聚类的直线数量和方向都具有一定的不确定性。为解决这个问题,本文在时频域中对X(t,k)进一步采用SSP检测,得到数据集Xssp,其散点图如图6所示。从图6可看出,Xssp的散点图明确地给出了6条直线,即反映了源信号的数目为6个。
为了应用密度基的聚类算法对观测数据进行分析,本文通过镜像映射方式(归一化处理)把线性聚类的数据Xssp转变为致密聚类的数据X*(k)。观测信号X*(k)的散点图如图7所示。
从图7可看出,X*(k)在上半个单位球上形成了密集的数据堆,信源的数量由数据堆的个数给定。尽管在密集的6堆数据之外也分布着某些数据点,但通过聚类算法的不断搜索即可实现这些数据的归类。
在利用数据集X*(k)对混合矩阵的估计过程中,各种算法的主要参数设置如下。对于K-means,聚类数量事先给定为K=6,初始聚类中心位置随机地生成,算法最大迭代次数为100,停止规则为产生的分配不再变化;对于HC算法,初始的每个数据点为一类,任意两点间采用欧氏距离,通过合并距离最小的两个类来发现数据簇,停止规则为合并后剩余类数量为6个。对于本文方法,DBSCAN算法的类簇邻域esp=0.04,密度阈值MinPts=10,把DBSCAN获得聚类数量作为CFSFDP算法的输入参数,CFSFDP算法中数据点之间采用欧氏距离,利用CFSFDP搜索密度峰值对聚类中心位置进行修正。这里对DBSCAN参数的选择说明如下。通过绘制观测数据X*(k)的K-距离曲线,找出该曲线的拐点位置,可得到对应的esp=0.04。而参数MinPts的选取原则为MinPts≥D+1,这里D=6,则MinPts≥7。在数据X*(k)的三维散点图中,密集数据堆外还分布着一些数据点,经计算可得这些点与最邻近数据堆的空间距离约为2个单位长度,即MinPts>7+2,于是取MinPts=10。
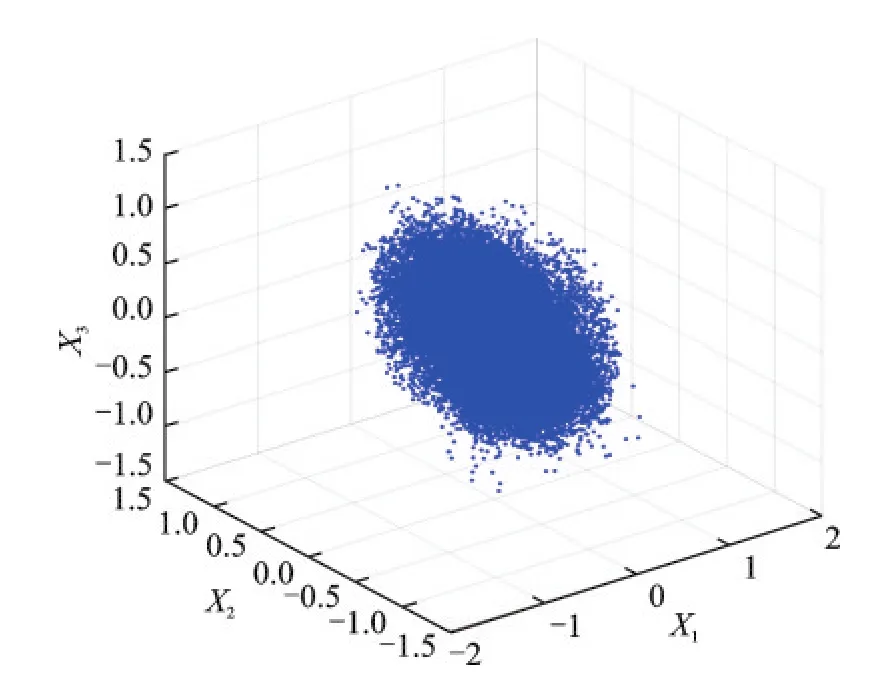
图43路观测信号的时域散点图Fig.4 Time domain scatter plot of three observed signals

图53路观测信号的时频域散点图Fig.5 Time-frequency domain scatter plot of three observed signals
经过本文方法、K-means算法和HC算法估计出的混合矩阵(记作B1,B2,B3)分别为
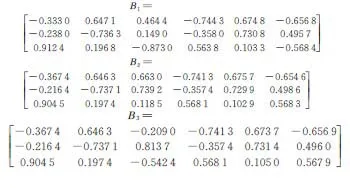
把原始混合矩阵A和各种方法估计得到的混合矩阵Bk(k=1,2,3)中各列向量代入到角度偏差d(a,b)和均方误差MSE的定义式中,计算得到结果如表1所示。
由表1可得出以下结论:(1)K-means算法对混合矩阵第3个列向量估计的角度偏差到达了71.6920,这是不能接受的结果;同样地,K-means算法估计的均方误差也比较大。(2)HC聚类算法的估计性能与K-均值算法基本相当,而它估计的均方误差是3种算法中最大的。(3)本文方法不但能够克服K-均值算法要求预先知道源信号数目的缺陷,而且估计的性能指标(无论是角度偏差还是均方误差)是3种方法中最好的,这说明本文方法在估计欠定混合矩阵方面是非常有效的。
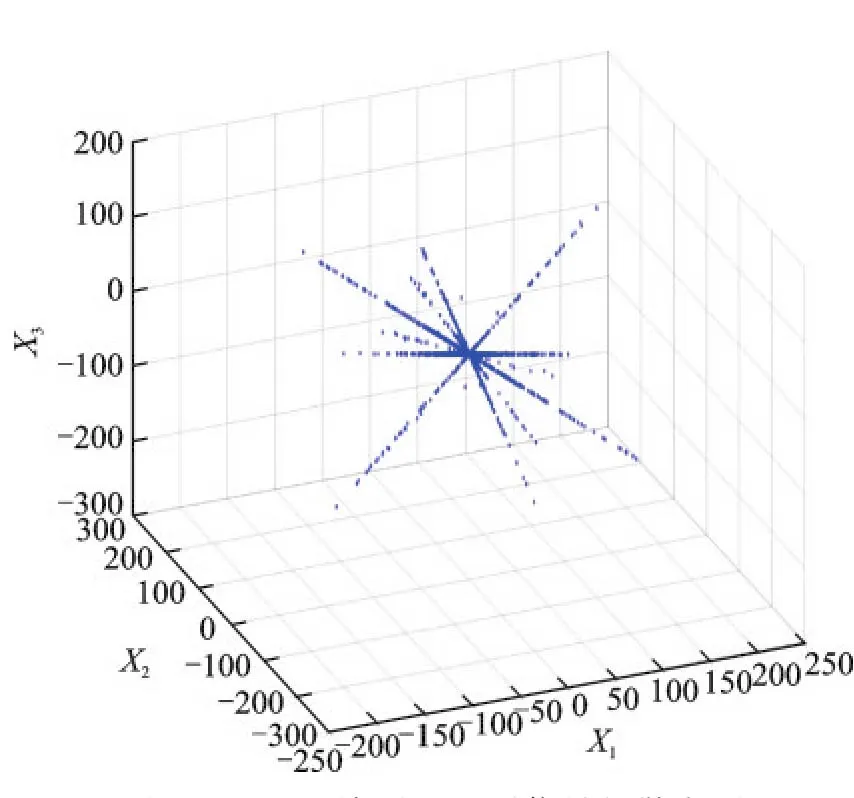
图6 经SSP检测后观测 信号的散点图Fig.6 Scatter plot of observed signals after SSP detection
本文方法在获得混合矩阵之后,利用最短路径法[3]对源信号进行恢复,并计算出原始信号与恢复信号的相关系数分别为:ρ11=0.9498,ρ22=0.9546,ρ33=0.9333,ρ44=0.9888,ρ55=0.9681,ρ66=0.965 2。各信号的相关系数均大于0.93,且6个信号的平均相关系数为0.96,这说明本文方法的估计量具有很好的一致性。
在以上的仿真中,仅仅做了一次实验。为了进一步测试各种算法对欠定混合矩阵的平均估计性能,在下面的仿真中,对类似的实验反复进行了15次。
在每次实验中,首先利用MATLAB函数rand(3,6)随机地生成一个3×6的混合矩阵A从而得到时域观测信号x(t)=As(t);然后通过STFT把时域信号转换成时频域的信号X(t,k),并对其进行SSP检测和归一化处理,得到观测信号X*(k);分别利用K-means,HC和本文方法对X*(k)进行聚类分析从而估计出欠定的混合矩阵;最后计算出估计的角度偏差和均方误差的指标值,并把15次实验的性能指标(角度偏差和均方误差)取平均值,得到结果如表2所示。

图7 经过归一化处理后观测信号的散点图Fig.7 Scatter plot of observed signals after normalization

表13种方法的角度偏差和均方误差值Tab.1 Angular deviation and MSE values of three methods

表23种方法的平均角度偏差和平均的均方误差值Tab.2 Average angular deviation and average MSE values of three methods
从表2可看出:K-means算法对于混合矩阵的第3,4,5列向量估计的平均角度偏差较大(大于1),其中第4列的平均角度偏差高达13.7576;而HC算法对第1,3,4,5列向量估计的平均角度偏差都很大,其中第5列的平均角度偏差竟然为18.0434,而且HC的平均MSE是3种算法中最大的。这说明利用K-means和HC算法对欠定混合矩阵估计的误差是很大的,因此会直接造成信源分离的精度下降。本文方法估计的混合矩阵列向量的平均角度偏差和平均MSE值都是这3种方法中最小的,除了第4列向量的角度偏差小于0.4之外,其他列向量的角度偏差都在0.07之下,这证明了本文方法对于欠定混合矩阵的估计精度很高。
在重复进行的15次实验中,对3种方法估计的混合矩阵,利用最短路径法分离(恢复)出信源,并对3种不同的方法,分别计算出每个源信号与对应的恢复信号的相似度。图8给出了3种方法每个信号在15次实验中相关系数的变化曲线。
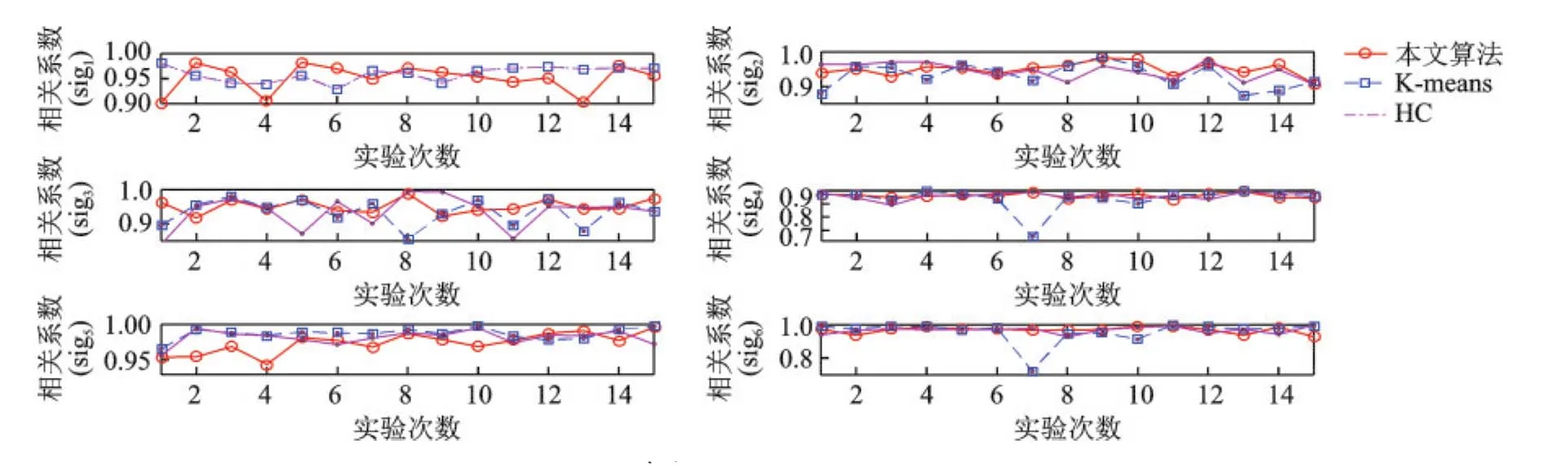
图8 每次实验中3种方法估计的信号相关系数Fig.8 Signal correlative coefficients estimated by three methods in each experiment
从图8可以看出,对于全部的6个信源(sig1,sig2,sig3,sig4,sig5,sig6),由K-means算法进行UBSS,所获得信号相关系数的最小值为0.6517,由HC算法获得相关系数的最小值为0.8407,而由本文方法获得相关系数的最小值为0.9015。因此,用K-means和HC算法恢复的信源与原始信源的相似度较差,也就是说,本文方法具有更高的信源分离(恢复)精度。同时还计算出了本文方法对每个信号在15次实验中的平均相关系数,它们的值分别是:0.9517,0.9508,0.9505,0.9616,0.9740和0.9673,把这6个信号的平均相关系数再取数学期望,则得到全部源信号的平均相关系数为0.9593,这是一个相当好的UBSS性能指标。
从以上的实验结果可以看出,本文提出的算法具有较好的欠定混合矩阵的估计性能。而算法在对噪声、信源相关性及欠定程度的适应性方面,具有以下的特性。
(1)在实际应用中,利用传感器采集信源的过程,不可避免地会使观测信号中包含有噪声。在UBSS中,噪声分为传感器噪声和信号源噪声两类,一般的BSS模型考虑的是传感器噪声[20]。对于本文算法,也进行了含噪声模型的实验,即在采集信号中加入高斯噪声,并通过降噪处理后再进行UBSS。在具有噪声的观测信号的信噪比(Signal to noise ratio,SNR)分别为20,15和10 dB的情况下,本文算法能有效地估计出混合矩阵并实现信源的分离。这就是说,本文算法对噪声的容忍度可达SNR=10 dB的恶劣环境。
(2)盲信源分离的主要方法是独立分量分析(Independent component analysis,ICA)[20],即假设信源是相互独立并且服从非高斯分布。然而,在对信源采集中,每个传感器获得的观测信号与邻近传感器信号不可避免是互相关的,这种相关性也可能发生在观测信号与非邻近传感器之间。对于具有互相关的信源,传统BSS/ICA利用信源高阶或二阶统计性质的方法将失效。为此,相关分量分析(Dependent component analysis,DCA)得到了广泛的应用。实际上,本文算法就是一种DCA方法,它是通过开发信源的稀疏性和非负性特征来实现对混合矩阵的估计;本文的单源点检测就是对信源稀疏性的增强;而对数据的归一化处理就是开发信源的非负特性。因此,本文算法对信源相关性具有较高的容忍度。
(3)对于欠定盲信源分离问题,传感器数量决定了BSS的欠定程度。本文算法的仿真实验中,在信源数量为6的情况下,分别取传感器数量为4,3,2,1进行了相应的实验。在传感器为4,3,2这3种环境下算法对混合矩阵的估计均取得很好的性能。而当传感器数量为1时,即单通道UBSS,本文算法对混合矩阵的估计性能急剧下降,恢复的信源产生了较大的误差。因此,本文算法对欠定程度的容忍度是要求最少有2个传感器。
(4)盲源分离中的信源一般是非高斯分布。在实际应用中,所遇到的非高斯信源,根据信号的峭度值可分为亚高斯信源和超高斯信源。本文讨论的音频信号属于典型的超高斯信源,而一些图像信号可能属于亚高斯信源。本文的BSS算法既可以分离超高斯信源,也可以分离亚高斯信源。对于属于亚高斯的图像信号盲分离应用,在文献[21,22]中有介绍。
4 结束语
本文基于稀疏信号的UBSS问题,首先研究了增强信号稀疏性的方法,利用STFT把观测信号从时域变换到时频域,并采用SSP检测剔除多源点数据,通过镜像映射把稀疏信号的直线聚类转变成致密聚类;然后,采用聚类分析的方法在密集的数据堆中寻找代表其方向的关键数据。为了克服K-means算法需要预先设置聚类数目的缺点,本文采用DBSCAN算法实现对数据的自动分类从而得到源信号数目以及初始的聚类中心;在此基础上,利用CFSFDP算法对DBSCAN获得的聚类中心进一步进行修正,以提高混合矩阵的估计精度。由于把DBSCAN的聚类数量作为CFSFDP的输入参数,也克服了CFSFDP需要人为干预的缺陷。

