基于物元分析法的温榆河水质评价初步研究
(华北电力大学 可再生能源学院,北京 102206)
近年来,随着社会经济的发展,水污染带来的环境问题也日益突出。在工农业生产和城市建设中,未达标、未处理的污水被排入河流,造成了严重污染。水质评价作为水资源保护、管理和利用的一项基本工作,成为污染治理、改善水质的重要一环。采用适当方法评价水质状况,对水污染治理和水资源管理决策提供科学可靠的依据具有重要意义。
目前,国内采用的水质评价方法有因子分析法、层次分析法、数理统计法等确定性方法和模糊理论法、灰色理论法、物元分析法、人工神经网络法、投影寻踪模型法等不确定性方法[1],这些方法各有优缺点。单因子评价法利用断面参评指标中类别最差的一项来评价断面水质,虽然简明易懂,但由于忽略了较优指标对水质的综合影响,其结果比较悲观。层次分析法(AHP)通过建立具有隶属关系的层次结构模型,并在一定标准化原则下构造判断矩阵,把问题归结为最下层相对于最上层的权重值及排序问题[2],具有较强的逻辑性和系统性。模糊数学评价法先对各单项参数进行评定,再根据各参数在总体中的重要性配以适当权重,再利用模糊矩阵复合运算得出综合评价结果[3],其结果常受权重值的影响而准确性较差。近年发展起来的人工神经网络也应用于水文领域,其在数据分析的基础上,通过对样本的学习和训练由计算机生成网络,消去了建模过程中的人为影响,且结果精确,有着良好的应用前景。
在诸多方法中,我国蔡文教授提出的物元分析法是解决矛盾或不相容问题的有力工具。本文通过水质物元模型的建立和物元分析法在温榆河水质评价中的应用,阐述了物元分析法的计算和建模过程以及物元分析法在水质评价中的优点。
1 基于物元模型的水质评价方法研究进展
物元分析理论的创立,为合理解决矛盾问题及不相容问题开辟了一条新的途径。作为一门新兴的横断学科,它不仅贯穿于自然与社会科学之间,还是思维、系统科学和数学的交叉学科[4]。它通过对事物可变性的研究,概化问题为相容与否,再通过各指标与等级区间的关联度大小定量地研究事物。在水质评价过程中,各个水质指标便是所研究水样的多个参数变量。通过物元模型研究水质状况,将水质指标、评价指标作为物元,通过关联度的大小得到各项指标的实测值与评价区间关联的紧密程度来判断水质的类别,能够较完整地反映研究水域的综合水质状况,还易于计算机编程处理,是水质评价的一种有效途径。
1.1 物元模型
对于研究的事物N,其特征C的值为V,即可用有序三元R=(N,C,V)作为基本元描述事物,该基本元简称为物元[5]。若研究事物具有多个特征,则可用c1,c2,…,cn分别描述它的n个特征,用v1,v2,…,vn分别对应n个特征的量值。可用矩阵表示为
(1)
可把具有n个特征的R称为n维物元,其特征的量值范围应在(an,bn)区间内。
在水质评价中,每个水质指标即为待评价水体的一个特征,而该水质指标的测量值为对应的特征值。由此,便可通过n个水质指标及其量值建立起研究水体的物元模型。
1.2 经典域和节域
对于具有多个等级的事物,可将每个等级上的特征及特征值范围作为物元模型的一个经典域。用矩阵表示为
(2)
式中:i为该等级内的特征个数;j为研究事物所具有的等级数。
经典域的直观含义即为事物某等级内各个特征量值的变化范围。
节域即为事物各个特征量值的变化范围。用矩阵表示为
(3)
在水质评价的物元模型中,将水质分为5个类别,每个类别各指标及其变化范围构成模型的一个经典域。而Ⅰ~Ⅴ类水各指标的变化范围即构成物元模型的节域。把水质测量结果用物元表示为
(4)
1.3 权系数和关联度
1.3.1 权重系数确定
各个等级评价指标的权重系数可使用“超标法”计算和确定:
(5)
(6)
式中:aij为各指标在各等级的权重系数;vij为归一化后各指标在各等级的标准;w0j为各指标5个等级标准的均值。
有时经计算得到的权重系数会大于1,此时需要对权重系数进行归一化处理。即
w′0j=w0j/∑w0j
(7)
1.3.2 关联函数及隶属程度的计算
关联度的计算采用关联函数[6],关联函数一般如下:
(8)
式中:Kj(xi)为各评价因子关于评价级别的关联度;ρ=(xi,V0ij)为点xi与有限区间Vij的距离,一般用如下公式计算:
ρ=(xi,V0ij)=|xi-0.5(aij+bij)|
-0.5(bij-aij) (i=1,2,3…n)
(9)
ρ=(xi,VPj)=|xi-0.5(aPj+bPj)|
-0.5(bPj-aPj) (i=1,2,3…n)
(10)
隶属程度即为待评价水体R0关于等级j的关联度,记作Kj(p0)。
(11)
1.4 等级评定
根据式(11)计算各个指标评价等级的隶属程度,可以对水质等级进行评价。关联度K(p0)>1,意味着所评价断面的水体状况大于一个级别要求的最大值;0 温榆河位于北京市东北部,发源于昌平,在防洪、排污和生态方面起着重要的作用。近年来,由于污染物的持续排放,温榆河的水质不断恶化。为对治理河道提供帮助,需通过物元分析法对温榆河进行水质评价。由于研究河段主要流经生活区,污染物主要来自于生活污水,评价指标选取该河段的主要污染因子pH值、DO、CODCr、氨氮。通过实地勘测,在温榆河上游的沙河水库、马坊、鲁疃闸和辛堡闸4个位置设置监测断面,情况见图1。 每月对温榆河4个断面进行水样采集并测量相应的水质数据。2017—2018年间每个断面共收集到12组数据,见图2。《地表水环境质量标准》(GB 3838—2002)相应标准见表1。 图1 温榆河水质采样断面 图2 水质指标测定结果 表1 水质评价指标及标准分级 选取2018年10月温榆河4个断面的水质数据进行水质评价,以说明物元模型在水质评价中的应用过程。 对各评价指标及监测值进行归一化处理,使各指标的量化值处于相同的区间。归一化后的评价指标及监测值见表2。 表2 归一化后的分级标准 取归一化处理后各级标准对应区间为经典域;由归一化处理后的标准值区间和实际测量值求算节域RP。 (12) (13) (14) (15) (16) (17) 由式(5)计算得到归一化后的权系数,见表3。 表3 归一化后的权系数 利用式(8)、式(11)计算得到10月4个断面的综合关联度,结果见表4。 表4 断面关联度及评价结果 计算及评价结果表明,2018年10月温榆河上4个断面的水质均为Ⅴ类水,符合实际情况,且与文献[8]中记录的温榆河水质状况相符,这也反映出温榆河水质恶化的情况。治理水污染,改善和提高温榆河的水质刻不容缓。 a.在上述水质评价的例子中,研究河段位于温榆河上游,流经北京昌平的主要生活区,其污染来源主要为生活污水,评价因子的选取以该河段的主要污染物为主,选取了溶解氧、化学需氧量、氨氮和pH值。水质评价的区域较小,且主要为生活区,参与评价的指标数量较少,是小区域的针对生活污水的水质评价。在评价过程中,物元分析法避免了单因子评价法忽略较优指标对水质综合影响的缺点,弥补了模糊数学评价法中因权重值偏差而导致的结果不准确的不足,且评价结果与实际相符。 b.物元分析法以水质评价指标及其特征值作为物元,在对评价指标及实测值归一化处理后,确定模型的经典域、节域,计算得到各个等级评价指标的权重系数和关联度,从而建立起对水质评价的物元模型,并得出评价结果。评价过程简单易懂,物理含义清晰明确,评价结果以定量的数值表示,且与实际情况相符,既能够准确完整地反映水质的综合水平,也能直观体现各污染指标的权重水平。由此可见,在水质评级中,物元分析法是一种行之有效的方法,能够为水质状况研究及污染治理提供科学可靠的依据。2 基于物元分析的温榆河水质评价
2.1 评价因子与标准


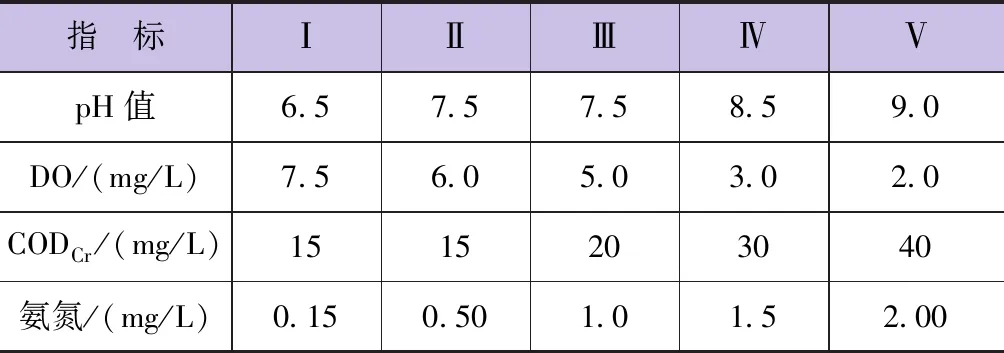
2.2 数据归一化处理
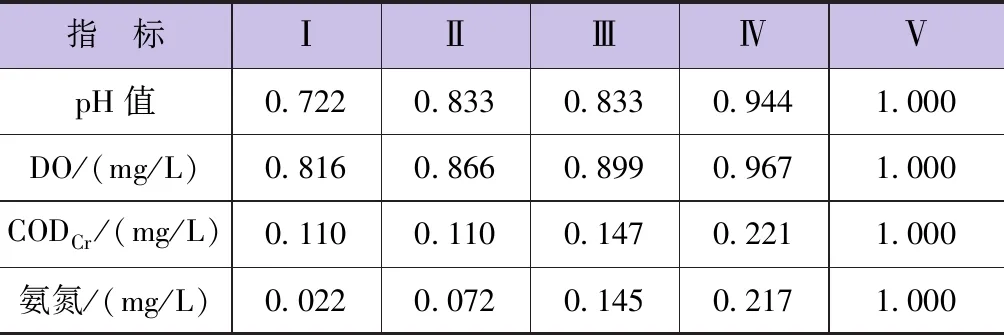
2.3 确定经典域矩阵和节域矩阵
2.4 计算权重系数和关联度
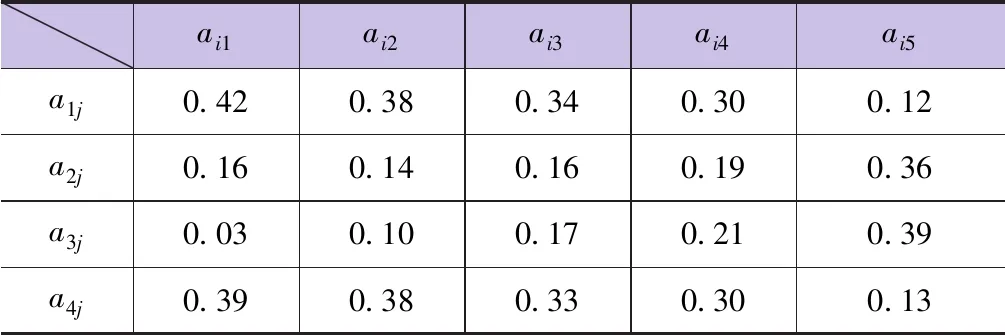
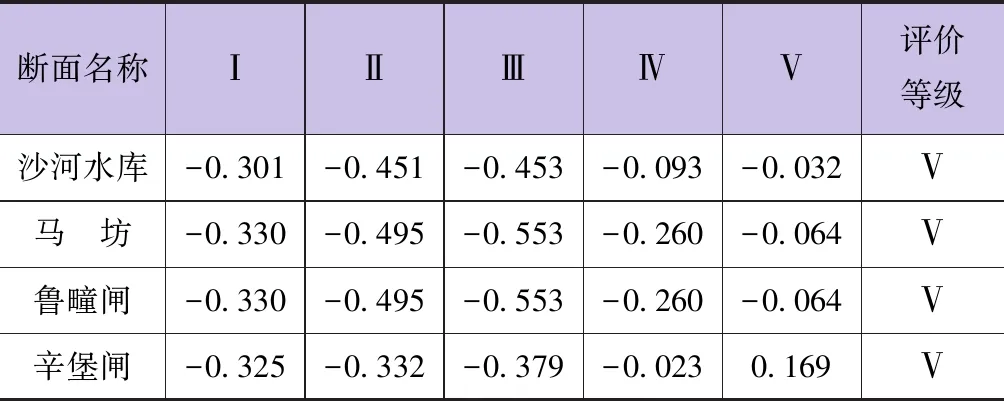
3 结 论

