基于离散优化的LP汽车总装线的配置模型研究

王诚

（兰州石化职业技术学院，甘肃 兰州 730060）

0 引言

汽车公司汽车总装线的配置是一个综合性排列优化组合问题，如何按照所提供的装配要求进行科学有效的设计，是降低成本、提高效率产能的关键。

本文针对2018年全国数学建模竞赛D题汽车总装线的配置问题进行了分析研究。考虑到汽车总装线的配置是一个离散模型的网络与组合优化问题，建立排序与时间表离散优化模型。采取启发式算法——分支定界法思路：靠下界控制搜索方向，若搜索到某一步比其他分支的下界大，就从下界小的分支继续搜索。

建立条件约束的离散优化LP模型，用MATLAB编程进行离散优化分析，给出了在工艺流程的制约和质量控制的需要以及降低成本的考虑下最优的装配方法，利用AHP模型进行满意度检验，对所建模型进行分析和改进[1-3]。

1 基本离散优化模型

考虑到汽车总装线的配置是一个离散模型的网络与组合优化问题，建立排序与时间表离散优化模型。

排序与时间表就是将不同的任务以一个执行的顺序和时间来安排，使得预定的目标最优化，比如时间最短、费用最省、效率或效益最大等。

针对装配要求，我们化繁就简，不考虑前期工件特别要求，在设置的2条生产线，两驱和四驱的装配要求及颜色的条件约束，加工时间较短，使得整个生产工艺流程成本较低。根据SPT（Shortest Processing Time）法则，可得到相应的最优加工顺序，但SPT不能直接应用于此题目。

采取启发式算法——分支定界法思路：靠下界控制搜索方向，若搜索到某一步比其他分支的下界大，就从下界小的分支继续搜索。最坏情况下，穷举所有可能的排列组合，这是一个隐含的穷举法，但在解决此类复杂的组合优化问题比较有效。

建立条件约束的离散优化LP模型：

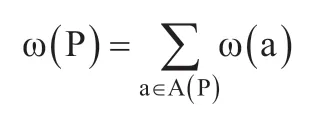
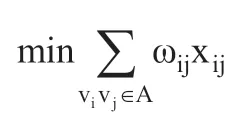
由于约束矩阵是全单位模的，即任何阶子式的值为1，-1或0，有研究结论说，整数线性规划当中的整数要求可以去掉而化为线性规则。所以，最优化问题可以用LP模型解决[4-8]。

2 实例应用

离散优化的LP汽车总装线的配置模型，按照题目给出的条件约束，运用MATLAB进行编程模拟，抓取主要影响参数，给出了具有较低成本的装配顺序。

针对题中条件约束，编程时受阻因素较多，程序多次运行失败。在只满足硬性要求时，也出现运行不下去的情况，适当调整了约束条件参数。同时没有考虑连续时间如17日到18日的时间衔接和互相影响因素，只研究每天的排列组合情况，这在实际生产过程中是降低成本的关键点。

3 模型的检验

利用AHP（层次分析法）模型进行满意度检验。

引入装配满意度对模型编写的装配顺序进行评价，问题对装配要求有4个一级指标，14个二级指标。

研究第2个一级指标，如：若间隔数量无法满足要求，仍希望间隔数量越多越好。间隔数量在5-9辆仍是可以接受的，但代价很高。将代价很高转换为装配顺序满意度，超过10辆满意度为100%，5-9辆之间的满意度设置如表1：

表1 第2个一级指标车辆间隔数满意度

同理可设置其他二级指标相对应满意度。

通过查阅资料，4个一级指标权重见表2。

表2 4个一级指标权重

经分析题目中所给二级指标的重要性，14个二级指标权重见表3。

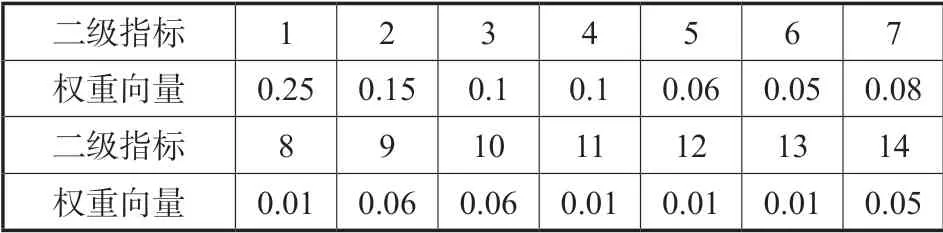
表3 14个二级指标权重

通过MATLAB编程计算分析：

9月18日无论如何分配黑色喷漆，均达不到50-70的条件约束；

9月23日，A1总计367，A2总计93，均为单数，导致白天和晚上无法平均分配进行装配。

其他时间满意度均能达到90%左右，9月18日和9月23日满意度在80%左右，综合整体装配顺序，模型满意度达到了90%以上，结果是满意的。

离散优化的LP汽车总装线的配置模型在每次程序搜索生成装配顺序时，可能结果都不一致，可运用AHP模型进行满意度检验，多次运行程序比较可得到相对最优值[9-14]。

4 模型的评价与改进

本文离散优化的LP汽车总装线的配置模型，可以借助LINDO、MATALAB、EXCEL-Solver等，也可将组合优化模型优化为整数线性规划模型。

采取连续化方法后模型比较复杂，无法求出问题解，只能退而求其次求出数值解。即建模时对离散变量做了连续化处理，而在求解时，对连续变量作了离散化处理。有时变量事实上只能取自一个有限元集合，如何建立相应模型并设计高效算法是非常重要的。

建立条件约束的离散优化LP模型是典型的NP问题。

经查阅相关资料，NP完全问题已经有几千个，包括最小Steiner树问题、Hamilton问题、最大点独立集问题、大多数的排序问题都属于NP完全类，这类问题的任意一个到目前为止尚未找到有效算法。

如何解决NP问题是目前求解的一大难点，采用穷举法不切实际。对题目中品牌分为A1和A2两种，配置分为B1、B2、B3、B4、B5、B6六种，动力分为汽油和柴油2种，颜色黑、白、蓝、黄、红、银、棕、汇、金九种，动力分为两驱和四驱2种。只讨论颜色和品牌，即为18种不同的产品，在生产线上出现的顺序排列方法有：18!/2 =1045094400 ≈ 3.2× 1 015之多。按照当前计算机处理数据能力每秒计算100亿=1010个排列情况，需要3.2× 1 05≈ 89小时 ≈3.7个日夜。再考虑其他4种因素，需要时间是呈数量级的增长[15，16]。

找出最优组合的排列顺序，如按照离散问题的穷举法思路，需要花费的时间是难以想象的，也不太可能实现。因此，在解决实际问题中，适当摒弃不合理数据和过多约束条件，是初步解决此类问题的一个有效途径。