基于Dempster-Shafer的飞行机器人多目标视觉定位方法

(西北工业大学 计算机学院，西安 710072)

0 引言

飞行机器人在没有外界干扰情况下能够完成飞行任务，但一旦受到外界干扰，对于飞行机器人的精确位置与姿态信息获取是相对困难的[1]。针对目前大多数飞行机器人装备的定位系统，受到定位精准度升级影响，导致定位系统每秒更新速度较慢，获取的数据也相对较少，且飞行机器人工作环境受到各种因素影响，导致定位系统存在较大局限性，因此，飞行机器人多目标视觉定位成为目前人们研究的热点问题[2]。正是飞行机器人能够灵活转向的特点，使其在军事、农业、物流等方面得到了越来越广泛的应用，通过预估自身位姿能够实现飞行机器人高性能运行，以此获取高精度导航数据[3]。

飞行机器人为了实现自主飞行，通过全球定位系统获取飞行器精确位置和姿态，但在室内环境中，全球定位系统信号受到空间限制，获取的信号相对薄弱，针对该现象，提出了基于扩展Dempster-Shafer证据推理的飞行机器人多目标视觉定位方法[4]。该方法的基本思路是：将接收到的信息作为定位信息源证据，给不同信息源分配不同的信任度，并支持证据对不同推理的精确描述，从而提高定位的准度。将证据推理描述信息源与基于不同位置定位方法结合可以有效弥补现有其他定位方法在对各接入点同等对待的不足，理论分析并结合实验结果验证了该方法的可行性，且方法使用效率高，适用性较强。

1 飞行机器人控制原理

飞行机器人如图1所示。

图1 飞行机器人

飞行机器人是世界上较为先进的信息搜索系统，用于罪犯跟踪，方便携带，也可部署于人群上空，方便监视工作。利用该机器人进行多目标视觉定位时，采用了Dempster-Shafer证据推理方法，该方法在不确定性度量上表现更为灵活，更加接近人自然思维习惯。就证据推理机制来说，对于任何一个信任更新后的证据都是通过合成规则来实现的，该推理过程透明可见，适用于任何机器。

针对飞行机器人的控制原理如图2所示。

图2 飞行机器人控制原理

根据图2可知，飞行机器人控制组件中，存在前后左右4个电机，其为220 v铜芯0.55/0.75/1.1/1.5 KW两相马达组成的，具备高密度精工轴承，安全耐用、温度低，采用全铜线圈设计方案，运行平稳，且使用寿命较长[5]。

飞行机器人位置和姿态控制是相互独立的，位置数据输出结果作为姿态控制输入数据，此时飞行机器人所在的具体位置是通过视觉定位方法进行计算的[6]。飞行机器人在空间的飞行位置与期望位置是存在一定偏差的，将该偏差结果作为横轴输入值，纵轴输出值作为姿态控制器的期望值。通过Dempster-Shafer证据推理可得到姿态控制所需的角度信息，并使飞行机器人达到预期位置[7]。

2 基于Dempster-Shafer多目标视觉定位方案的实现

通过Dempster-Shafer证据推理多源信息融合定位方法实时获取飞行机器人捕获的彩色图像和深度图像，并手动选取目标区域，提取相关边缘特征，按照一定权值系数来构建目标模板[8]。利用多目标跟踪定位方法实时捕捉多个目标位置信息，将此结果全部输出，获取三维位置坐标。

2.1 特征提取

2.1.1 颜色特征提取

飞行机器人对颜色特征进行提取时，对于图片变化并不敏感，因此当目标被遮挡时，飞行机器人获取的图片受到影响程度较小，适用于对多目标的描述。对于颜色特征提取可通过HSV颜色空间进行描述，由于亮度值与多目标物体反射比有关，因此，容易受到外界光照影响，导致用色度分量和饱和度分量形成了二维直方图，这对于目标的构建是具有一定影响的[9]。针对该问题，需将图片的HSV颜色空间按照直方图，将用色度和饱和度子空间量转化为等份空间，使每个空间都构成一个直方图空间。

2.1.2 边缘特征提取

图片中的多目标轮廓包括了丰富特征，一旦出现多目标被遮挡现象时，图片的轮廓边缘变化十分明显，因此，需通过计算区域图像中的像素梯度才能得到边缘信息。为此，需采用Canny算子对图片进行处理，首先计算水平方向梯度值，然后计算垂直方向梯度值，最后计算梯度幅值和方向[10]。由于多目标的边缘信息通常是在360°空间中获取的，因此，梯度方向只能反应出180°的多目标轮廓信息，依据梯度幅值的横纵坐标可将180°的多目标轮廓信息转换成360°的多目标轮廓信息。通过统计直方图，可将360°空间等分成18份，以此保证不同区间内图像像素点个数一致，由此确定多目标的边缘信息特征。

2.2 多目标模型建立

根据上述提取的颜色特征和边缘特征，使用Bhattacharyya系数将特征信息融合起来，选定的多目标模板颜色特征随着选定区域扩大，信息内容越丰富，此时目标颜色模板与候选的模板是相似的，这与之前模板也是完全匹配的。

多目标模型构建具体流程为：

1)选定目标边缘特征；

2)将两种特征信息转化为巴氏距离；

3)利用高斯函数构建似然函数；

4)对似然函数进行加权融合处理；

5)确定权重后，对地面标记进行设计。

2.3 地面标记设计

设计地面标记，通过不同形状填充多边形。为了保持飞行机器人在设定周期内进行飞行，需对其进行实时控制，对于图形中的不同特征进行提取，当图形数量满足设定的个数时，具有良好稳定性。此时，标记坐标系原点，组成地面标记的多边形信息。飞行机器人进行实时采集时，需先标记地面位置，通过图像传输将图片特征信息传入地面计算机之中，以此进行基于Dempster-Shafer多目标视觉定位计算。

在进行计算前，需先对飞行机器人捕捉到的图像进行处理，处理流程如下所示：

1)安装机载摄像头，由此获取图像；

2)对图像进行预处理；

3)进行轮廓检测；

4)特征提取；

5)将提取的结果输入到已经训练好的分类器中进行处理，由此获取不同形状的对应信息。

根据上述内容，完成地面标记设计。

2.4 分段多目标跟踪定位

通过迭代算法能够快速对目标进行局部最大化概率计算，以此适应多目标形变，一旦目标被遮挡，那么将会造成多目标极大值点出现个数变多，此时分段多目标跟踪定位结果出现偏差，坐标信息也将全部丢失。分段多目标跟踪定位方法对于目标遮挡问题能够较好地追踪目标，但相对于位置信息的选取是相对严格的，当信息获取数量较多时，其分布的例子概率密度逐渐逼近于后验证的概率函数密度，跟踪精准度较低。

在整个跟踪过程中，需依据Bhattacharyya系数将特征信息融合起来，通过Dempster-Shafer证据推理对当前帧建立目标模型。经过迭代处理后，捕获到候选目标，依据选取的目标进行相似度判断，如果相似度大于设定的阈值，那么说明多目标没有被遮挡，飞行机器人继续跟踪多目标；反之，如果相似度小于设定的阈值，那么说明多目标被遮挡，此时不应更新目标模板，直接切换成Dempster-Shafer证据推理方法进行跟踪。通过相似度与阈值对比的方法，能够在多目标未被遮挡情况下，确保良好跟踪效果，而一旦目标被遮挡，那么该方法能够增强跟踪的实效性。

分段多目标跟踪定位方法具体实现步骤为：

1)通过飞行机器人捕获当前帧彩色和深度图像；

2)依据当前获取的图片颜色和相关特征构建初始化目标模型；

3)在搜索窗内对目标质心位置进行搜索；

4)依据目标与候选目标相似度，判断飞行机器人多目标视觉物体是否被遮挡，如果未被遮挡，则需返回到步骤3)，如果被遮挡，则需采用Dempster-Shafer证据推理方法对多目标进行视觉跟踪；

5)根据上述追踪到的结果选定目标颜色，收集相关信息进行初始化处理，并依次赋予权值；

6)通过高斯分布对赋予的权值进行扩散处理，依次获取新的位置信息；

7)通过位置信息计算不同颜色与边缘融合特征，并进行模板匹配，依据Bhattacharyya系数计算选定目标和候选目标之间的相似度，通过该相似度对目标进行更新，并赋予权值重新采样；

8)选取最大权值作为目标跟踪结果，由此获取二维坐标，依据坐标信息计算目标所在位置矩形框，并返回到步骤4)。

2.5 多目标视觉定位方案的实现

通过分段多目标跟踪定位获取的坐标信息与之对应的点以及飞行机器人内部参数，计算摄像机方位，通过Dempster-Shafer证据推理方法对飞行机器人位置进行估计，并使用虚拟控制点表示多目标位置的点。

将摄像机透视问题转化为摄像机坐标下的控制点问题，通过标记的坐标点表示摄像机坐标系下的坐标点，以此构建成像模型。利用相机小孔成像的模型参数矫正成像模型，获取图像坐标，采用最小二乘法能够获取摄像机内部参数，由此能够获得n维未知向量。对地面标记的目标点进行识别，如果出现的点数不能完全被识别，通过识别出其中几个点就能获取目标位置信息，由此实现多目标视觉定位。

3 实验

实验针对基于Dempster-Shafer的飞行机器人多目标视觉定位方法进行研究，为了测试该方法在被遮挡情况下的定位效果，进行了飞行机器人穿过教室实验。将该方法与Camshift方法在飞行机器人视觉定位准确率和效率两方面进行对比分析；为了提高定位结果精准度，需进行静止定位实验，计算其与期望中的误差，以此验证该方法的定位精准度。

3.1 实验环境

本实验选在Wi-Fi环境下，实验场地示意图如图3所示，过道中部署60个采样点采集接收到的RSSI来构建位置数据库，设最小采样点间距为1米，主要将采样点布置在各房间门前，每个采样点按照每秒采集1个RSSI的频率来采集。实验场地示意图如图3所示。

图3 实验场地示意图

3.2 飞行机器人飞行定位实验

在上述实验环境下，放置教室空间模型作为遮挡，通过平台获取图像信息，在该平台上沿着直线进行移动，使其通过教室，并保证飞行机器人在移动过程中的平稳性。在曲线飞行状态下，实际运行轨迹如表1所示。

表1 曲线飞行状态下实际运行轨迹

在直线飞行状态下，实际运行轨迹如表2所示。

表2 直线飞行状态下实际运行轨迹

分别使用两种方法跟踪定位，其跟踪结果如图4和图5所示。

图4 两种方法跟踪定位曲线飞行比较结果

由图4可知：由于飞行机器人在曲线飞行时保持匀速飞行状态，所以无论时间多少，其飞行的轨迹大都一致。当时间为10 s时，传统方法X轴方向飞行的位置为480 mm，y轴方向飞行的位置为750 mm，Z轴方向飞行的位置为1 750 mm；基于Dempster-Shafer方法X轴方向飞行的位置为250 mm，y轴方向飞行的位置为275 mm，Z轴方向飞行的位置为2 250 mm；当时间为40 s时，传统方法X轴方向飞行的位置为600 mm，y轴方向飞行的位置为750 mm，Z轴方向飞行的位置为1 650 mm；基于Dempster-Shafer方法X轴方向飞行的位置为240 mm，y轴方向飞行的位置为280 mm，Z轴方向飞行的位置为2 250 mm，这与实际运行轨迹一致。

由图5可知：当时间为2 s时，传统方法X轴方向飞行的位置为750 mm，y轴方向飞行的位置为900 mm，Z轴方向飞行的位置为1 490 mm；基于Dempster-Shafer方法X轴方向飞行的位置为500 mm，y轴方向飞行的位置为650 mm，Z轴方向飞行的位置为2 100 mm。当时间为8 s时，传统方法X轴方向飞行的位置为260 mm，y轴方向飞行的位置为700 mm，Z轴方向飞行的位置为1 600 mm；基于Dempster-Shafer方法X轴方向飞行的位置为100 mm，y轴方向飞行的位置为150 mm，Z轴方向飞行的位置为2 000 mm，这与实际运行轨迹一致。

依据上述对比结果，将飞行机器人曲线和直线飞行的数据进行分析，发现其与实际轨迹期望的距离还是存在一定偏差的，因此，采用EVPS测量数据具有较小测量误差，并能够与真实数据进行对比，满足飞行机器人实时控制的需求。为了验证该方法精准性，依次对传统方法与基于Dempster-Shafer方法定位误差累积概率进行对比分析，如图6所示。

由图6可知，当误差距离为1 mm时，基于Dempster-Shafer方法定位误差累积概率为0.1，传统方法定位误差累积概率为0.3；当误差距离为3 mm时，基于Dempster-Shafer方法定位误差累积概率为0.12，传统方法定位误差累积概率为0.5；当误差距离为6 mm时，基于Dempster-Shafer方法定位误差累积概率为0.18，传统方法定位误差累积概率为0.85。由此可知，基于Dempster-Shafer方法在飞行状态时定位误差较小。

3.3 飞行机器人静止定位实验

基于Dempster-Shafer方法计算获取的飞行机器人多目标视觉定位的二维位置坐标，需结合相关数据获取三维位置坐标信息，为了验证该方法精准度是否满足飞行机器人位置信息输入的精准度要求，需在其静止状态下进行跟踪定位。分别采用Dempster-Shafer方法和传统方法对飞行机器人静止状态下的三维位置误差进行对比分析，结果如图7～8所示。

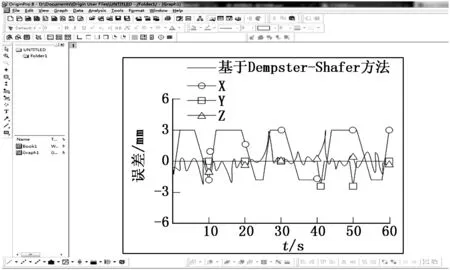
图7 Dempster-Shafer方法下的三维位置误差曲线

图8 传统方法下三维位置误差曲线

由图7、8可知，传统方法X轴方向最大误差为3 mm，最小误差为0 mm；Y轴方向最大误差为2.7 mm，最小误差为0 mm；Z轴方向最大误差为2.5 mm，最小差为0 mm。基于Dempster-Shafer方法X轴方向的曲线呈有规律性的上下变动状态；Y轴方向呈现直线状态，当时间依次为40 s和 50 s时，误差达到最大；Z轴方向的曲线呈无规律性的上下变动状态。X轴方向最大误差为3 mm，最小误差为0 mm；Y轴方向最大误差为3 mm，最小误差为0 mm；Z轴方向最大误差为2.7mm，最小误差为0 mm。由此可知，飞行机器人在静止状态的三维位置误差较小。

3.4 实验结果与分析

基于Dempster-Shafer的飞行机器人多目标视觉定位结果精准度与传统方法对比结果如表3所示。

由表3可知，当实验次数为1、2、3、4、5次时，采用Dempster-Shafer方法飞行状态下的飞行机器人多目标视觉定位精准度比传统方法依次高52%、53%、54%、53%、55%；在静止状态下的飞行机器人采用Dempster-Shafer方法对多目标视觉进行定位的精准度比传统方法依次高43%、43%、45%、46%、47%。

表3 两种方法定位结果精准度对比分析

综上所述：无论是在飞行机器人飞行定位实验还是静止定位实验下，基于Dempster-Shafer方法比传统方法定位精准度要高。

4 结束语

针对飞行机器人多目标视觉定位，提出了Dempster-Shafer方法，在飞行机器人被遮挡情况下也具有较高定位精准度。实验结果表明，提出的Dempster-Shafer方法解决了定位精准度低的问题，可广泛应用于自主飞行的机器之中，完成飞行任务。在一定误差范围内，通过地面标记能够识别多目标，并在机载视觉下也能进行精准定位。

下一步工作应充分利用该方法的高精准定位性能对飞行机器人的位姿进行测量，保证飞行机器人能够完成复杂动作。