应用网络模块度的航天测控地面站网分析

汪筱阳，朱 琳2，朱参世3，张亚奇，徐 浩，王引娣

(1.中国西安卫星测控中心，西安 710043； 2.中国人民解放军95607部队，西安 710000；3.西京学院 信息工程学院，西安 710123)

0 引言

航天测控地面站网由多个测控站、测控中心和通信系统构成[1]。根据国际空间数据系统咨询委员会(CCSDS)提供的世界测控站目录，可供联网的测控站分布在四大洲，数量近百个。如何合理配置不同的航天测控地面站，形成全域、稳定、最优的测控网是高效发展航天事业的重要研究方向。同时，精确划分不同专用航天测控地面站可以为地面站的配置提供重要支持。

目前，许多学者都对航天测控地面站网进行了一些有益的探索性研究。文献[2]对航天测控系统进行了分类，总结了美国的卫星测控网、载人航天测控网、深空网和军事航天测控网等不同类型测控系统及其发展历程，分析了美国航天测控系统发展的特点与趋势。文献[3]认为企业级地面体系(EGA)代表了飞行器测控的发展方向，通过对EGA的研究，总结了美军构建通用军事测控系统的总体设计思路及设计原则。文献[4]介绍了美军航天测控网中的共享测控网和专用测控网，阐述了空军卫星控制网、陆军卫星控制网、海军卫星控制网以及5种主要专用测控网的地面段分布情况、操作机构及功能，分析了美军航天测控网的发展趋势。文献[5]分析了欧空局通信网的组成，认为澳大利亚和西班牙深空地面站的相似性，使广域网的拓扑结构得到了优化。文献[6]分析了印度深空探测测控系统的发展情况。综上，我们发现几乎所有对航天测控地面站网的研究都是从测控系统及测控技术的角度分析，通过测控系统建设情况和技术应用来预测航天测控网的规划方向、发展趋势。然而，全球上百个航天测控地面系统构成的网络，它们必然存在一些网络应该具有的属性，通过网络的视角来分析航天测控地面站网，将为我们研究航天测控地面站网打开另一扇门。

近年来，随着信息科学技术的飞速发展，各学科理论及应用呈现出交叉、渗透和融合的发展趋势[7]，使得网络科学迎来了蓬勃的发展[8-9]。复杂网络是复杂系统的抽象，它无处不在[10-11]，许多现实系统都可以抽象为网络模型进行研究[12]。文献[13]研究了复杂地震网络，加利福尼亚、日本和印度这3个复杂地震网络的聚集系数将收敛于0.85。文献[14]研究了社会和信息网路中的采样网络，用不同的采样方法分析了采样网络中的节点特性，认为采样信息网络能用相同结构的节点模块进行更好的描述，并且采样网络比原始网络更能表现社区性质。文献[15]研究了全球金融市场目录信息传播网络的拓扑结构性质，将该网络抽象为一个有向加权网络，发现网络具有小世界性质。文献[16]研究了航空维修安全网络，通过定义安全信息辐射模型和规则，基于改变维修人员本质安全度和网络结构分析了网络节点状态的变化。文献[17]运用复杂网络方法研究了地震活动中的信息交互，利用信息论和基于复杂网络的地震活动模型将通信过程进行了量化，对于地震活动的过程有了更深的理解。因此，可以将复杂网络方法应用于航天测控地面站网，用网络属性来描述航天测控地面站网的一些性质，对其进行定性或定量的研究，找出其中存在的一些潜在规律，能为航天测控地面站网的发展提供一些理论探索和支持。

本文运用复杂网络方法，首先建立了航天测控天地一体化二分网络，然后根据二分网络结构及测控系统和航天器之间的物理意义，通过Kendall相关系数和提出的相关网络参数建立了地面测控系统相关性网络，并对网络模型的有效性进行了验证，最后分析了网络参数对网络模型的影响，得到了一些有益的结论。

1 航天测控地面站网络模型构建

航天测控地面站网并不是独立存在的，它的建设依赖于航天器的发展。因此，航天器的需求制约着航天测控地面站的类型和布局。在航天领域发展早期，由于科学技术的现实局限性，世界各航天大国在航天测控通用性方面均缺乏一种整体思维，这就导致了各国在航天发展初期建立了多个航天测控地面站网，它们互相独立、自成体系。以美国为例，为了针对不同的航天任务，其建立了卫星跟踪与数据获取网(Spacecraft Tracking and Data Acquisition Network，STADAN)，载人航天网(Manned Space Flight Network，MSFN)，深空网(Deep Space Network，DSN)，美国空军的卫星控制网(Air Force Satellite Control Network，AFSCN)等。随着科学技术的革新，为了整合资源、节约成本、提高效率，美国的专用航天测控地面站网的测控设备逐渐进行了改造和替换，使之能够满足多种航天器的需求，具备了一定的通用性。

综上可知，并不是每一个航天测控地面系统都能满足所有航天器的需要，也不是每一个航天测控地面系统只能满足某一个航天器的需要。如果将所有的航天器和地面测控站看成一个网络的话，那么可以将这个大网络分成两类节点，一类为航天器，另一类为地面测控系统。若某个地面测控系统能满足某个航天器的需要，则在这两个不同类别节点之间建立一条边。这个天地一体化网络示意图如图1所示，从图1可知，天地一体化网络为二分网络。

图1 天地一体化网络示意图(H表示航天器，C表示地面测控系统)

目前，针对二分网络的研究有许多方法[18-20]，但是本文为了更专注的研究航天测控地面站网络，希望在天地一体化网络的基础上形成一个航天测控地面站子网络，该子网只有地面测控系统一类节点。为此，我们需要把地面测控系统从天地一体化网络中剥离，这里对天地一体化网络数据进行处理。网络数据及处理步骤如下：

步骤1：在美国STADAN、MSFN、DSN、AFSCN网络实际的基础上来得到模拟数据。由文献[2]可知,4个专用测控网的地面测控系统约为15套，假设与每个专用测控网对应的航天器有100颗，每个专用测控设备有一定概率α满足该测控网对应航天器的需要，有一定概率β满足其他测控网对应航天器的需要。

步骤2：建立测控系统-航天器矩阵H={hij}m×n，矩阵的行代表测控系统，数目为m=4×15=60，矩阵的列代表航天器，数目为n=4×100=400，若第i个测控系统能满足第j颗航天器的需要，则hij=1；否则hij=0。矩阵示意图如图2所示。

步骤3：借助二分网络结构特性，根据每个测控系统满足航天器需要的情况，计算测控系统两两之间的相关性，这里采用Kendall相关系数来计算矩阵H的第i行和第j行之间的相关性Kij。

步骤4：建立测控系统-测控系统矩阵C={cij}m×m，矩阵的行、列均代表测控系统，数目为60，设置测控系统相关性阈值为K0，若测控系统i、j之间的相关性Kij>K0，则cij=1；否则cij=0。

步骤5：根据矩阵C构建航天测控地面站相关性网络。其中，测控系统即为网络中的节点，测控系统之间的相关性为节点之间的连边，若cij=1，则在测控系统i、j之间建立连边；否则没有连边。

由此，可以得到航天测控地面站相关性子网络。

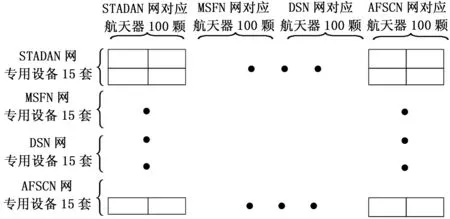
图2 测控系统-航天器矩阵示意图

2 仿真与分析

由航天测控地面站相关性网络模型可知，在网络规模确定的情况下(m=60)，网络的结构与α、β、K03个参数有关。也就是说，若已知网络规模及α、β、K03个参数就可以确定地面站相关性网络的结构。

2.1 模型有效性验证

就军事卫星通信系统来说，美国防部、美空军和美海军分别部署了近十套独立系统。这些系统只能实现地面站、用户终端与空间卫星的信息传输，既不能在宽带网络中传输信息，也不能与采用其他系统的卫星实现连接。为了模拟美国地面测控网现状和验证网络模型的有效性，假设各专用网络所属的测控系统的专用性较高为α=90%，通用性较低为β=10%。相关性阈值K0=0.3。则航天测控地面站相关性网络如图3所示。

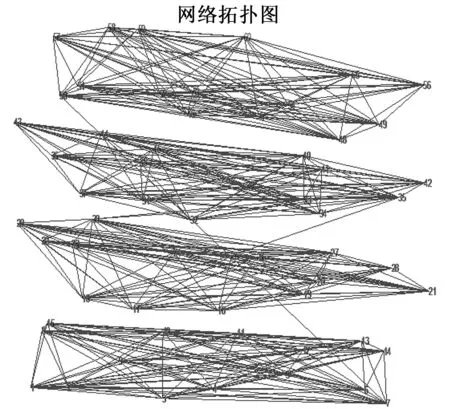
图3 航天测控地面站相关性网络拓扑图

从图3中可以看出各专用测控系统的相关性得到了很好的划分，在网络中形成了很明显的社团结构，验证了美国发展了大量的专用卫星测控网，而且这些网络较为封闭，不与其他网络共享测控资源和人员，测控系统并不具有互通性，表明了美国测控系统重复建设和相互隔离难以互操作的问题。由于仿真条件中测控系统存在10%的概率具有通用性，因此在图3的网络中也存在极少量社团之间的连边，这些少量连边代表不同社团之间的连接节点具有相关性，说明这些连接节点起到了其所在社团与其他社团之间的交流作用，他们的介数较高，并且可以作为各社团的中心节点方便社团内部节点与其他社团节点进行信息交流。

为了更好地验证模型的有效性，这里首先介绍模块度的概念。模块度是常用的一种衡量社团划分质量的标准。对于给定的实际网络，假设找到了一种社团划分，那么所有社团内部的边数的总和可计算如下：

(1)

其中:A={aij}是给定网络的邻接矩阵，节点i与节点j在网络中所属的社团分别用Si,Sj表示：若节点i与节点j同属一个社团，则δ=1；否则δ=0。

若利用相同的社团来划分与该给定网络相对应的一个相同规模的零模型，则所有社团的内部边数总和的期望值是:

(2)

其中:pij是零模型中节点i与节点j之间的连边数的期望值。

综上，网络的社团内部边数与相对应的零模型的社团内部边数之差占整个网络边数M的比例即为网络的模块度：

(3)

在理论上，对于与原网络具有相同度序列但不具有度相关性的一个常用的零模型[21]，有pij=kikj/2M，这里ki和kj分别为原网络中节点i与节点j的度。

综上可知，在相同规模网络下，模块度越大，说明社团分割的结构准确性越高，另外，把每一个节点视为一个社团时，模块度恒为负。可以计算出图3的模块度为0.740 6，模块度较大，说明按照相关性阈值0.3得到的社团划分较为合理。因此，该网络模型能较好地说明美国航天测控网的现状，验证了网络模型的有效性。

2.2 模型参数分析

由于美国卫星基础设施的建设和维护工作分散实施，不利于各建设和维护机构之间的技术和经验交流，容易造成资源浪费。所以，为了改变航天测控网分散建设实施导致的“烟囱”式系统现状，打破各专用测控网之间的界限，测控系统之间的通用性将是未来航天测控的发展趋势。这里首先对参数β,K0进行分析。为了消除概率产生的随机性误差，下述图中每个数据点为进行100次仿真取平均值。

当固定参数α=90%，β取不同值时，航天测控地面站相关性网络的相关性阈值与模块度曲线(K-Q曲线)如图4(a)所示。

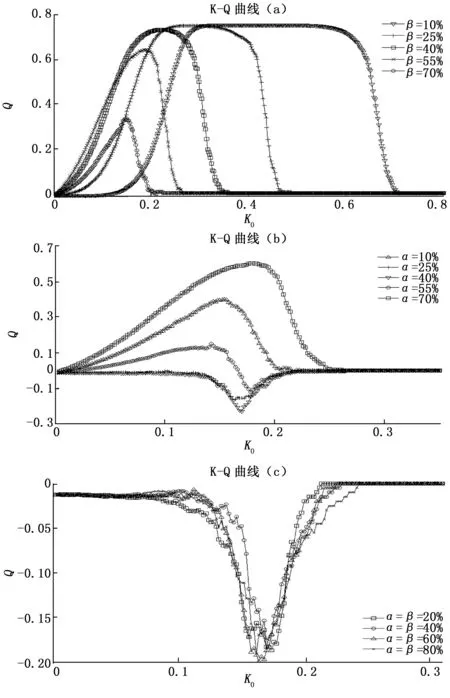
图4 航天测控地面站相关性网络K-Q曲线图

从图4(a)可以看出，第一，在不同的测控系统通用性下，随着相关性阈值(K0)不断增大，网络的模块度(Q)不断增大，即社团的划分越来越优化；当K0增大到一定程度之后，Q达到峰值不再增大，此时社团划分到达最优，能较好的区分各个专用测控系统；当K0继续增大，Q逐渐降低，最后降到0，此时将不能区分各个测控系统，分析原因是因为α≠1且β≠0，说明各个专用测控系统内部的设备之间也存在或大或小的差别，不存在一模一样(相关性为1)的测控系统；第二，随着β的不断增大，Q的峰值不断降低，说明β的增大会影响网络社团的划分，使各个专用测控系统不易从测控网中区分开来，当β=70%时，Q值很小，基本不能区分网络中的社团，也说明了此时各个专用测控系统的通用性很强，极难从网络中找到各个专用测控系统；第三，随着β的不断增大，Q到达峰值时K0的取值不断减小，说明各个专用测控系统之间的相关性不断减弱，只有不断降低K0才能尽量区分网络的不同社团；而且Q到达峰值时K0的区间不断缩短，说明要想尽力找到各个社团的话，对K0的取值要求也越来越精确。值得注意的是，由于中心极限定理的原因，K-Q曲线整体呈现出正态分布特性。

当固定参数β=40%，α取不同值时，航天测控地面站相关性网络K-Q曲线如图4(b)所示。

从图4(b)中可以看出，Q的峰值和α并不相关，而是与|α-β|呈正相关，即|α-β|越小，Q的峰值越小。分析原因为α和β分别代表了测控系统满足各自专用航天器和其它航天器的概率，在所构建的网络模型中，这两个概率也是各专用测控系统与其他测控系统的唯一区别，所以，它们是辨识各专用测控系统的标志，也就决定了网络社团划分的模块度大小。当α和β差值越大时，说明测控系统之间的差异越大，不同专用的测控系统的相关性越小，社团分割的结构准确性越高，所以模块度峰值也就越大。同时，随着α和β差值增大，Q到达峰值时K0的取值和取值区间也越大，说明网络的社团划分越容易。另外，图4(a)中的曲线也验证和说明了这一结论的正确性。

为了更充分地说明上述结论，分别令α=β=20%，α=β=40%，α=β=60%，α=β=80%时，航天测控地面站相关性网络K-Q曲线如图4(c)所示。图4(c)表明，只要α=β，网络模块度均为负，不能对网络进行社团划分，也就不能在航天测控地面站相关性网络中区分出各专用测控系统。

3 结论

随着未来不断增多的航天任务需求和日益急迫的空间对抗需求，各国都在寻求对现有航天地面系统的转型，航天测控地面站系统正不断演化为越来越复杂的网络化系统，包括属于其中的通信网络、电力网络等。目前，美国和欧洲军、民、商各方都在研究通用航天地面系统，通用化不仅减少了网络攻击风险，而且采用先进的信息技术可以提高航天地面系统的性能、安全性、弹性、灵活性。但是，通用航天地面系统的建设必须考虑在整个航天测控地面站网络层面的多种专用测控资源的整合，而研究航天测控地面站的相关性可以为测控资源整合提供理论指导和依据。

本文抓住航天测控地面站网作为网络的本质特点，从天地一体化二分网络出发，提出了测控系统专用性和通用性参数并利用Kendall相关系数和相关性阈值来构建航天测控地面站相关性网络，通过实例分析，验证了网络模型的有效性，然后仿真分析了网络模型参数，发现该网络的模块度与专用性和通用性参数的差值呈正相关。虽然得出了一些有益的结论，但是所提模型对于航天测控地面站网络的构建来说比较简化，其中还有很多细节值得下一步深入研究。