一种综合孔径微波辐射计成像处理算法

陈海建 丁孝永 王 锐

(1.海军驻北京地区舰空导弹系统军事代表室，北京 100039；2.北京无线电计量测试研究所，北京 100039；3.32182部队，北京 100039)

1 引 言

微波辐射计具有厘米波的全天候特性和红外的高分辨率优点，对于金属、危险品可有效地探测和成像，对隐身目标有很好的可探测能力，在海洋、大气、土壤遥感和安检等很多方面有广泛的应用前景。虽然微波辐射计拥有很多优点，然而传统的微波辐射计存在空间分辨率较低，成像质量有待提高的问题。因此微波被动成像技术研究和发展的主要方向就是如何获得更好的空间分辨率以及研究更好的反演成像方法和技术手段。

为了在不增加天线体积的情况下，满足实际应用中高分辨率的要求，获得更好的成像效果，在微波辐射计的天线设计中引入射电天文学中的干涉综合孔径技术。利用方向和长度不同的基线所组成的基本单元“二元干涉仪”来完成空间频率域采样，这种方法代替了传统微波辐射计对空间域的直接测量。国内外在该方法研究上取得了一些成果，如华中科技大学的用Tikhonov正则化的G矩阵反演算法[1]对HUST-ASR的成像试验数据进行图像重建处理的方法，利用FFT反演加匹配滤波的方法[2]降低辐射计误差的方法；电子科技大学的迭代梯度反演法[3]等。

为提高微波辐射计成像分辨率，减小图像噪声，本文提出一种综合孔径微波辐射计成像处理算法。

2 微波辐射计原理及构成

微波辐射计采用被动接收目标电磁波并进行成像的原理，实现对被测目标的探测。其主要由接收机子系统、天线扫描控制子系统、环境控制子系统、地面定标子系统、测试数据处理子系统和主控系统组成，如图1所示。

图1中，主控系统软件发送命令，由扫描伺服控制子系统实现二维转台的扫描控制；通过天线与接收机子系统，实现对被测物体的电磁信号接收和变换，由高速数字采集系统完成对射频信号的采集、数据接收。测试数据处理软件结合扫描控制的坐标信息和数据接收的数据信息，生成辐射图像。地面定标子系统在测试前后完成对微波辐射计的标定。

图1 微波辐射计系统组成框图Fig.1 Microwave radiometer system frame

3 综合孔径成像

为解决天线口面尺寸与成像分辨率的矛盾，提高微波辐射计成像分辨率，通常采用综合孔径成像方式。综合孔径成像是基于干涉仪成像的一种成像方式，干涉式成像辐射计天线的基本结构由二元干涉仪组成，通过两个天线单元进行相乘干涉来测量入射电磁波的角度和幅度信息。对于远场入射的电磁波，其波程差信息仅依赖于干涉仪的基线和电磁波入射角度，并且可以通过干涉测量的相位信息反映出来。干涉仪的相关输出结果即可见度函数的一个采样为

(1)

式中：Ωkl——天线波瓣立体角；(ukl,ukl)——两天线单元的有效距离；(ξ,η)——观测角度的方向余弦；TB(ξ,η)——场景辐射亮温；Fn——天线归一化场强方向图；rkl——相关接收机的去相关函数。

当系统带宽非常窄时，rkl≈1。因此，在理想情况下，可见度采样函数与亮温分布可由傅里叶变换联系起来。

(2)

可见干涉仪实现的是对空间频域的采样，因此对干涉测量结果进行逆傅里叶变换便可得到场景的亮温分布。

4 滤波反投影成像算法

成像算法的本质是对式(2)进行求逆运算从而得到亮温图像[4]。本文借鉴CT理论中的研究成果，从投影变换的角度出发来分析圆周极网格采样数据。对于二维平面中的任意函数f(x,y)，其投影变换(也称为Radon变换)定义为

(3)

式中：δ——迪拉克(Dirac)函数。

投影变换的几何意义为：函数f(x,y)沿直线xcosθ+ysinθ=s进行线积分，积分结果即为函f(x,y)在该射线上的投影值p(s,θ)。可见(s,θ)为积分直线的法方程参数。p(s,θ)表示图像函数在距圆点距离为s法线倾角为θ的直线上的积分值。因此投影函数是由一系列线积分组成。不失一般性，同时也对应于干涉辐射成像的实际情况，可以将函数f的定义域限制在单位圆内：x2+y2≤1。图2中给出了函数f(x,y)在θ角的平行投影函数p(s,θ)。

图像函数的投影变换与其傅里叶变换有着紧密的联系，图像的投影数据与其频谱可以直接互相转换，这种转换关系可以由中心切片定理来描述为

(4)

式中：p——关于变量s的一维傅里叶变换；f——空间频域点(u,v)上的傅里叶变换。

因此，中心切片定理可以简化表示为

Pθ(w)=F(w,θ)=F(wcosθ,wsinθ)

(5)

式(5)就是中心切片定理的核心内容，也是成像算法的关键。因为图像函数的二维极坐标傅里叶变换对应于投影数据的一维傅里叶变换，而当干涉成像仪的天线系统采用直线阵结构进行旋转扫描采样时，其所得到的空间频域采样点分布正好是圆周极网格结构，每个角度的天线阵采样点都均匀分布在一条直线上，正好可以对应于此角度下的图像函数的平行投影，如图2所示。

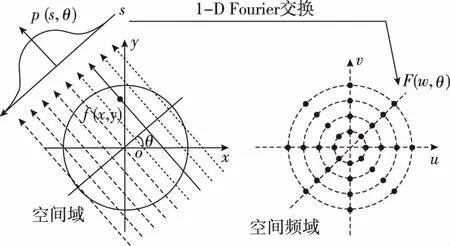
图2 平行投影以及中心切片定理示意图Fig.2 Parallel projection and the central slice theorem diagram

因此成像反演时可以考虑直接将空间频域采样转换成图像函数的投影数据，然后再利用投影变换的求逆方法进行图像重建，这样就避免了在空间频域进行插值，从而提高了重建图像的精度。

下一步需要求解投影变换的逆变换，即对式(5)进行求逆。很早Radon便导出了逆投影变换公式为

(6)

然而上式并不适合实际应用，主要是由于含有微分算子，不但不便于实际操作，而且具有很强的噪音放大作用。因此实践中都不采用逆投影变换公式。根据极坐标下的逆傅里叶变换公式以及采样数据的共轭对称性有

(7)

根据中心切片定理，将式(5)带入上式后，并令s=xcosθ+ysinθ，可得

(8)

其中，

(9)

式(9)相当于将空间频域函数P与响应函数为H(w)=|w|的窗函数进行加权后做逆傅里叶变换，其描述的反投影运算可以看作是一个将滤波后的投影数据沿原方向“涂抹”到像平面中的过程，是对各个角度采样数据处理的一种累加积分过程，而各角度的滤波投影数据可以相互独立地进行“涂抹”运算。在反投影计算时需要在空间域进行插值来求得像素位置的函数值，一般线性插值便可取得很好的效果。

根据以上论述，对于旋转扫描干涉成像情况，需要对天线阵在每个角度的空间频域采样数据进行加窗求逆傅里叶变换，然后再做反投影来得到原始图像的重建图像。加窗反投影重建算法的基本过程如图3所示。

需要注意的是，窗函数H(w)=|w|不可避免地会造成空间域信号出现吉布斯(Gibbs)震荡现象，在重建图像中表现出一定的波纹效应。因此，需要用特定的窗函数进行处理，其目的在于控制采样数据中的噪声，以提高重建图像的清晰度和平滑感。

4.1 小波增强去噪

常见的图像增强、去噪处理方法一般都是在时域或频域选择一种进行处理。它们都具有各自的优点和缺点。小波分析方法[5]是一种可以同时在时域和频域对图像进行处理的方法，在进行低频处理时增加了其频域分辨率同时加入了时间分辨率；对于高频部分虽然频率分辨率较低，但是加入了客观的时间分辨率。这样的特性使得小波变换对信号有很好的适应性。

a)小波去噪

如图4所示，通过二维小波分解得到各层系数的模，再进行去噪[6]，然后对处理后的小波系数进行小波重建，最终得到恢复后的图像。这里最重要的是对阀值的具体估计。阀值是噪声和图像信息之间的一个动态判别值，阀值太小会降低去噪效果，图像中会残留一部分噪声；反之便会滤去图像中的部分重要图像信息。

图4 小波去噪原理框图Fig.4 Wavelet denoising functional block diagram

b)小波增强

小波增强技术就是将一幅原始图像分解为大小、位置和方向都不同的分量，在逆变换之前，可根据需要对不同位置不同方向上的某些分量改变系数大小，得到感兴趣的图像，其原理框图如5所示。

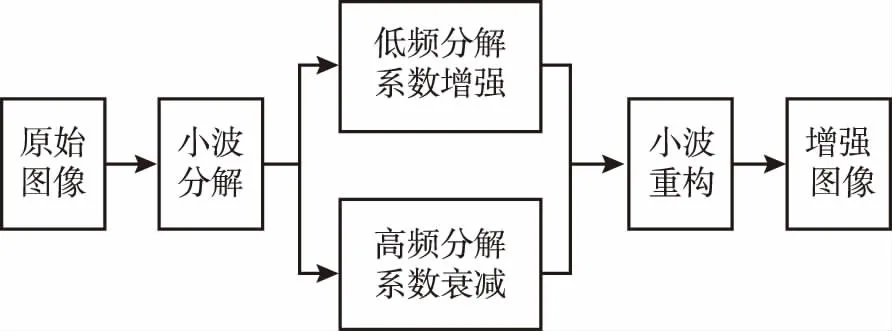
图5 小波增强原理框图Fig.5 Wavelet enhancement functional block diagram

小波增强是将分解后的低频或者是高频分量系数进行线性加权，达到增强需求信息抑制非必要信息的目的。

5 超分辨率算法

图像反卷积技术被用于提高空间分辨率，这种算法主要聚焦在矫正天线方向图的低通滤波效应。超分辨率算法[7]可实现系统截止频率之外的信息复原，因此必然是非线性的，其主要基础有解析延拓理论和Harris方法。Harris提出并经Goodman重新表述的这种超分辨率方法的基本思路是：设空域有界函数f(x)及其频谱F(s)，若f(x)通过一个截止频率sm为线性系统，则可确知-sm≤s≤sm内的频谱，但若希望恢复-sn≤s≤sn(sn>sm)内的频谱，则可按照式(10)进行估算

(10)

式中可看做一个含有2N+1未知数的方程，未知量为F(2nT)在各采样点处的值，由于|s|≤sm内的频谱已知，故可在此频段内选择2N+1个频率点代入式(10)中，因此可求解出上述方程组。

目前常用的超分辨率算法有能量连续降减法、Bayes法、最大熵法和凸集投影法(POCS)等[8,9]。其中前两者算法由于算法中为引入先验知识，它们的超分辨率能力是有限的；而后两者算法的运算量极大，收敛速度慢。本文选用一种盲解卷的Lorentzian算法，该算法是在Lorentzian算法的基础上，借鉴了最大似然算法思路，可在不能确知系统函数的情况下进行盲解卷。

5.1 Lorentzian超分辨率算法

Lorentzian算法是通过对图像的导数图像引入了约束。设原始图像为f(i,j)，则其导数图像可定义为

(11)

其中，

δx(i,j)=f(i,j+1)-f(i,j-1)

(12)

δy(i,j)=f(i+1,j)-f(i-1,j)

(13)

已有大量实验表明，自然辐射图像的导数图像的概率密度可用Lorentzian函数来近似，其中Lorentzian函数定义为

(14)

式中：α——表示图像尖锐程度的参数；

由导数图像中各点可认为是相互独立的，则其整体密度函数为

(15)

以此先验信息作为一种约束用于图像恢复中，作辅助函数为

(16)

式中：λ——拉格朗日因子。

对Q求导并令其为零，经计算整理有

其中，

(17)

对式(17)作傅里叶变换，可得

D+λ[G-FH]H*=0

则可解得

(18)

(19)

作傅里叶逆变换，即有

(20)

实际中取迭代算法，即

(21)

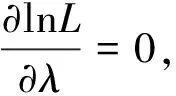
(22)

其中，δb(k,l)的求法如同式(19)，只需将f替换成b即可。

显然，以上计算过程需要确知系统函数h(i,j)。但在实际的成像系统中，很少有能确知系统函数h的情况，因此必须寻找在无准确h的情况下的算法。

图像退化模型式为

g(x,y)=f(x,y)*h(x,y)+n(x,y)

(23)

式中：g(x,y)——所获得的退化图像；f(x,y)——原始图像；n(x,y)——加噪声。

(24)

5.2 Lorentzian算法仿真验证

为了验证上述算法，利用二维图像进行仿真。其原始图像由三个不同灰度的同心圆组成，原始图如图6所示。该图像经过高斯型系统函数退化并由噪声污染后得到的图像如图7所示，可见图像失真很严重。经算法处理后的图像如图8所示，算法中使用的是真实系统函数，可见图像质量有明显改善。

6 结束语

本文介绍一种采用干涉仪成像原理的综合孔径成像方法，从理论算法上解决了采用综合孔径微波辐射计的成像问题，并通过窗函数滤波和小波增强去噪算法提高了成像的图像质量。最后，采用盲解卷的Lorentzian超分辨率算法提高成像的分辨力，较好的解决了天线口面与分辨力矛盾的问题，提升了微波辐射计的成像分辨力。