一种基于RSA的改进安全算法

(河南理工大学 计算机科学与技术学院，河南 焦作 454000)

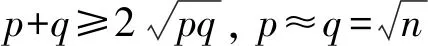
1 RSA算法相关研究工作

1.1 公钥加密技术原理

公钥密码体制的公钥公开，私钥保密。使用公钥进行加密，私钥解密，具体操作过程如下(如图1所示)：用户A有一对密钥对，分为公钥和私钥，这对密钥对唯一。当破解加密信息时，只有获得了与其配对的私钥，才能把加密信息解密出来。具体如下：用户A生成密钥对后，把它的私钥保存好，把公钥公开出去，当一个用户B要与A通信，就可以使用A的公钥来加密信息，再把密文传给A，此时只有A手中的私钥才能对这个密文进行解密，这样就确保了信息的安全。

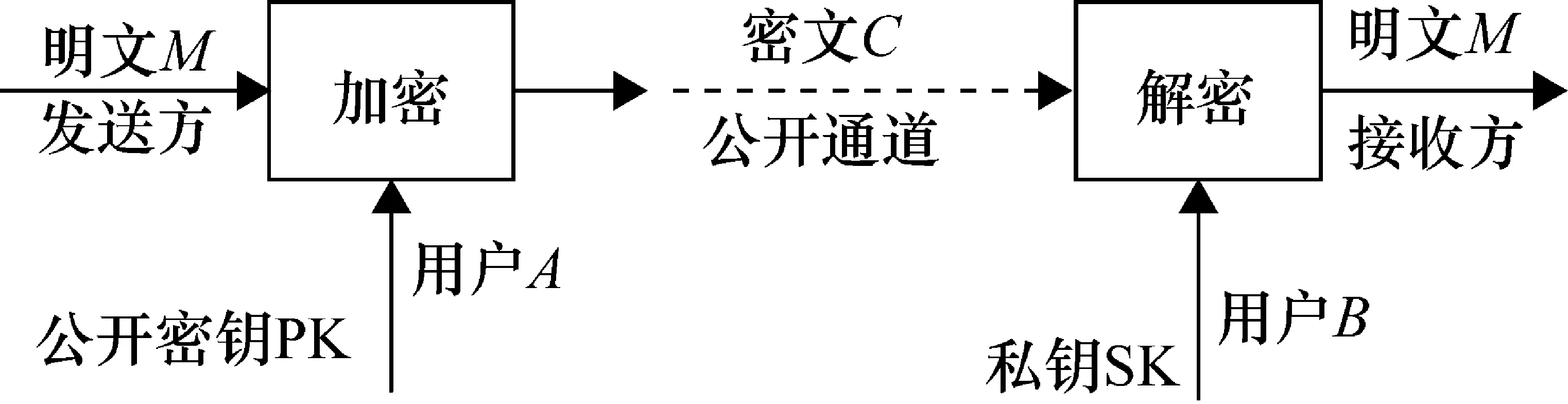
图1 用户A与用户B之间的公钥加密

1.2 公钥经典传统RSA加密算法

传统RSA算法的安全性依赖于大数分解[1]和素性检测理论。这也是RSA算法的安全性理论支撑，一般情况下安全密钥产生步骤如下：

① 选取两个大的不同的素数p和q，计算n×q和φ(n)=(p-l)(q-l)(不公开)。

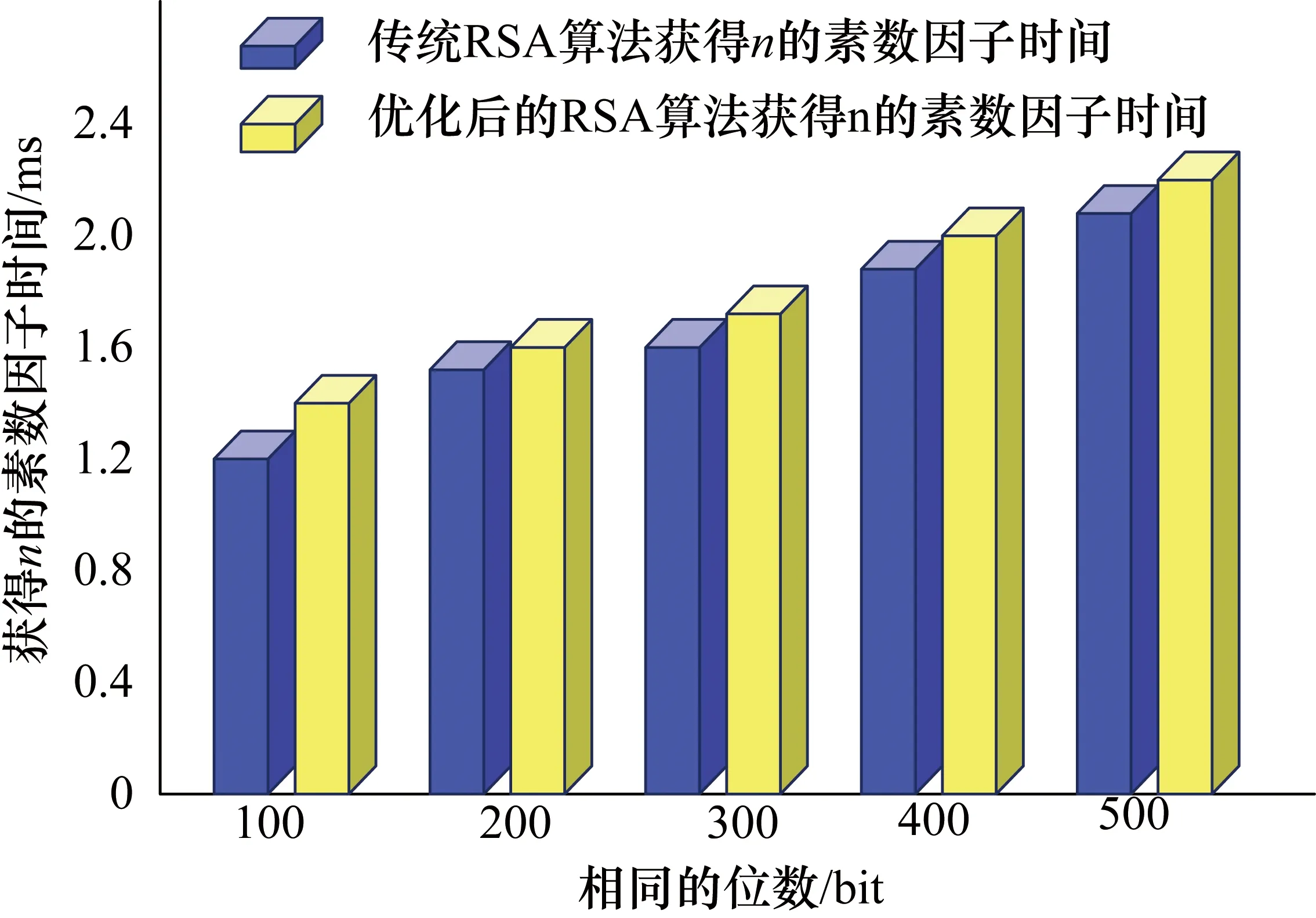
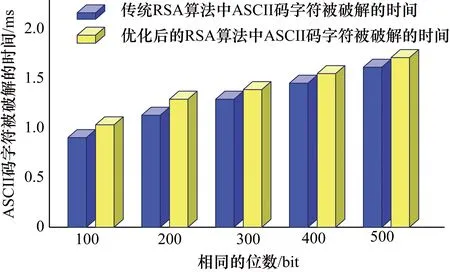
② 选取加密密钥e，且满足0

③ 求出密钥d，满足de≡lmod(φ(n))。这样就产生公钥(e,n)和私钥(d,n)。

1.3 指数2k次方化算法和代数结构算法

对于RSA算法存在着安全性被攻击的可能，许多学者对此提出了不同的改进算法，这里介绍2k进制化算法和代数结构算法。

指数2k进制化算法是通过缩短指数长度来减少迭代次数的一种优化算法。该算法先计算gximodn，Xi={0,1,2，…，2k-1}，从g0modn到g2k-1modn的每一个值，并将其存放在数组R中，再进行幂剩余和同余计算：赋变量c=1，对于i=m-1,…,1,0，不断执行c=c2kmodn和(c×R[xi])modn,最后得出c。

代数结构算法中，应用二次剩余理论，给出Z×φ(n)中元素阶计算公式和最大阶表达式，计算Z×φ(n)中二次剩余个数，估计出Z×φ(n)中元素的最大阶上限为φ(φ(n))/4。

上述两种算法的思路是：基于减少迭代次数的2k进制化算法和二次剩余理论的代数结构算法。算法中存在着结构简单的缺陷[2]，安全性受到挑战，对此，本文提出一种改进算法，实验证明：此算法相对于传统算法，在安全上有一些提高。

2 RSA算法的优化与改进

2.1 密钥优化方法

在密钥优化方法中，先增加大整数分解的素数个数，再增加每两个素数之间的距离，接着再对相应的ASCII码进行同或操作加密。在大整数n中，n的5个素数因子p、q、r、s、t选取方法是：先确定素数p和q，再在p和q的基础上使r=p×1.033，s=q×1.026，t=p×1.029，此时把r,s,t,用p,q表示代入n=pqrst，得n=p×q×(p×1.033)(q×1.026)(p×1.029)。为进一步增强算法的安全性，也采用了双字符加密思想，在数据加密前，对n的5个素数因子进行ASCII编码时，使生成的ASCII码与相邻的前一个ASCII码进行同或操作加密，加密结果会受到前一个字符的影响。在做解密算法的时候，只需要做相应的逆运算即可。

以五素数为例，C代表密文，M代表明文，E代表加密算法，D代表解密算法，算法过程描述如下：

① 选取大整数n，使n分解为5个不同的素数；

② 生成5个素数p、q、r、s、t；

③ 计算n=pqrst(公开)，n的Euler函数φ(n)=(p-l)(q-l)(r-l)(s-l)(t-l)(保密)；

④ 选取正整数e，1

⑤ 计算d，满足同余式del(modφ(n))(保密)。

加密和解密过程与双素数时完全一样，仍然为：

① 加密过程：C≡E[M]Me(modn)。

② 解密过程：M≡D[C]≡Cd(modn),其中M是明文，C是密文。

从大整数分解的难度知：密码优化前后，大整数因子被破解的时间对比图如图2所示。

图2

如图2所示，通过密码优化前后，获得大整数n的素数因子时间对比，优化后的算法安全性有所提高。

2.2 算法结构改进

本文设计出一个RSA改进算法，在不改变n的情况下，把一个大整数n分解成5个素数的乘积，使r=p×1.033，s=q×1.026，t=p×1.029，对于分解的5个不同的素数，采用ASCII码进行编码，使ASCII码均与其前一个ASCII码进行同或操作加密。这样提高字符之间的相互制约性，增强了算法的安全性。

在RSA算法中，如果大整数n被因式分解，就意味着私钥已经泄露了。为了保证RSA算法的高安全性[3]，可以通过增加密钥的长度来实现，伴随着密钥长度的增加，大整数n被破解的概率更小，只要n不被破解，RSA算法的安全性就会受到保障。

2.3 运算操作改进

2.3.1 大整数n的分解

在大整数n中，取n的两个因子p和q，以p和q为基准点，使(n/p)mod(q)=0，取其中另一个因子近似103.3%q,(n/pq)mod(102.6%q)=0，直到(n/pqrs)mod(102.9%s)=0,从而确定出p、q、r、s、t，使n=pqrst，根据RSA算法原理，首先确定出表达式φ(n)=(p-1)(q-1)(r-1)(s-1)(t-1)。

2.3.2e和d的选取

接着再选取一个正整数e，使e满足1

以PK=(n,e)作为公钥，SK=(n,d)作为私钥，在公钥密码体系中，E和D分别为加密和解密的代名词。

加密和解密过程为：加密过程：C≡E[M]=Me(modn)，解密过程:M≡D[C]=Cd(modn)，其中M是明文，C是密文。

2.3.3 每两个素数之间的距离进行选取

5个素数中，为实现每两个素数之间的距离有所增加，采用了先确定素数p和q，再在p和q的基础上使用r=p×1.033,s=q×1.026,t=p×1.029的策略，针对这样的构思，策略如下。

先是设定两个素数p，q的值，使(n/p)mod(q)=0，取r的近似值为103.3%q，使(n/pq)mod(102.6%q)=0，直到(n/pqrs)mod(102.9%s)=0，从而确定出p、q、r、s、t。

在方案中，5个素数的代表字母为p、q、r、s、t,根据RSA算法中的构造方案，n=pqrst,

φ(n)=(p-1)(q-1)(r-1)(s-1)(t-1)

=(pq-p-q+1)(rs-r-s+1)(t-1)

=pqrst-(prs+qt)+1

令pqr=m，qt=k则φ(n)≈n(m+k)+l,m×k=n,φ(n)≈mk(m+k+l)

然后得(m+k)=nφ(n)+1,mk=n,构造成方程式为x2-[n-φ(n)+1]+n=0，m,k为方程式的两根。

C≡E[M]=Me(modn),de≡1(modφ(n)(保密)，解密过程:M≡D[C]=Cd(modn)。

2.3.4 对分解的5个素数进行ASCII码转换

当大整数被5个素数进行因式分解时，对于生成的素数，先转换为对应的ASCII码，表1为大整数n分解的素数信息中截取的一部分(65，67，69，69，73，76，80，80，69)转化成对应的ASCII码。

表1 部分素数因子对应的ASCII码

然后每个ASCII码与自己前面的邻近ASCII码进行同或操作，进行加密。转换后的ASCII码与相邻ASCII码同或操作的部分结果如表2所示。

表2 转换的ASCII码与相邻前面ASCII码的同或操作

2.3.5 对转换的ASCII码进行同或操作

把大整数n分解的5个素数因子p、q、r、s、t,转换为对应的ASCII码[4]，并使转换后的ASCII码与前一个ASCII码进行同或操作，表达式为Mi=Mi⊙Mi-1(1

3 安全性证明及应用分析

3.1 安全性证明

3.1.1 改进的算法素数选取的安全性

改进后的RSA算法中，针对素数[6]的个数增加到5个，并且5个素数中的每两个素数之间的间距是增大的，选取每两个素数中的两个，即a和a+x，使gcd(a,a+x)=1,先是设定两个素数p，q的值,使(n/p)mod(103.3%p)=0，依次类推：取下一个因子r近似103.3%p，使(n/pq)mod(102.6%p)=0，直到(n/pqrs)mod(102.9%s)=0。在改进的方法中gcd(a,a+x)=1，使两个素数近似相等的概率降到零，从而很难知道素数的范围，增强了破解[7]的难度，相比传统的RSA算法[8]，安全性有了一些提高。

传统的RSA 算法一般使用两个素数p，q用来保护信息的安全，φ(n)=(p-1)(q-1)=pq-(p+q)+1=n-(p+q)+1破解p,n之后,q是很容易被破解的，从而造成RSA的加密算法被成功破解。改进的方案中使用5个素数，在方案中，5个素数的代表字母为p、q、r、s、t，根据RSA算法的构造方法，n=pqrst,φ(n)=(p-1)(q-1)(r-1)(s-1)(t-1)，令prs=m,qt=k,则φ(n)≈n(m+k)+1,m×k=n,φ(n)≈mk(m+k)+1，然后得(m+k)≈n-φ(n)=1,mk=n,构造成方程式为x2-[n-φ(n)+1]+n=0,m,k为方程式的两根。

在二元二次方程式中，只有一个方程式的前提下，基本上是没有解的，在上面的方程式中，x1和x2的解是比较难解[9]，基本上是无解，因此，n是很难破解的。由上面可以看出，改进后的RSA的算法，安全性有一些提高。

3.1.2 RSA算法的加密改进

改进后的RSA 算法，先大整数分解成5个不同的素数，再把对应的素数转换为对应的ASCII码。

表3是大整数分解的素数，素数中对应的部分ASCII码，接着把对应的ASCII码与相邻前一个ASCII码进行同或操作加密，如表4所示。例如，部分信息 65，67，69，69，73，76，80，80，69。

表3 信息位数对应的ASCII码

表4 对应ASCII码与相邻前面ASCII码间同或操作

第2行第1列的空格进行同或运算[10]时，字母A与其他字母进行同或操作，有两种结果，即0或1。

分析知优化算法与传统算法ASCII码字符解密的时间比(如图3所示)，由数据分析知，安全性提高了。

图3 密码优化前后ASCII码字符被破解的时间对比

由于每个ASCII码会受到前一个字符的影响(如图3所示)，所以破解的难度进一步加大。从上面分析可知，改进的RSA算法相比于传统的RSA算法安全性，有一些提高。

3.2 理论分析

D[C]=Cd=(Me)d≡(modn)de≡1(modφ(n)),
de=1+kφ(n)：D[C]≡Med(modn)=M1+kφ(n)(modn)
=M(Mφ(n)k)modn

gcd(M,n)=1时，根据欧拉定理[11]:得出Mφ(n)=1(moe)n，即D[C]=M;若gcd(M,n)≠1时，又因为n=pqrst,根据素数的定义gcd(M,n)等于p,q,r,s,t中之一或是pq,pr,qr,ps,qs,rs,st,pt,rt或是pqr,pqs,qrs,prs,rst,prt,qrt之一或是pqrs,pqrt,prst,qrst。

分4种情况进行解密,使D[C]=M。

①gcd(M,n)等于p,q,r,s,t中之一；

②gcd(M,n)等于pq,pr,qr,ps,qs,rs,st,pt,rt中之一；

③gcd(M,n)等于pqr,pqs,qrs,prs,rst,prt,qrt中之一；

④gcd(M,n)等于pqrs,pqrt,prst,qrst之一。

假设gcd(M,n)=p，则可以推出M=tp,其中t是正整数。1

D[C]=M(Mφ(n))k(modn)=M+tns≡M(modn)

成立。再进一步假设gcd(M,n)=pqr,有M=tpqr,这里t为正整数。θ1

4 结束语

本文对传统的RSA 算法进行了改进，采用了5个大素数，使大整数[12]具有了5个不同的素数因子，先确定素数p和q，再在p和q的基础上使r=p×1.033,s=q×1.026,t=p×1.029，同时对素数产生的字符进行加密，使每一个字符与它的前一个字符进行字符运算，然后再进行加密。相比于传统的RSA算法，增强了算法的安全性，提高了破解的难度。