基于U模型的Buck变换器控制器设计

(江南大学 物联网工程学院，江苏 无锡 214122)

随着能源需求的急剧增加，功率变换器作为一类典型的开关非线性系统，已在军事设备、工业自动化设备等领域得到广泛应用。因此，针对功率变换器的动力学特性分析、建模以及控制器设计研究，具有一定的理论价值和实际工程意义。常规的功率变换器控制器设计方法有两种：一种方法是线性化使用线性控制策略，如PID控制、极点配置控制[1]等，但变换器的参数变化会给线性控制器的设计带来极大困难；另一种方法是使用非线性控制策略,例如滑模控制[2]、模糊PID控制[3]、神经网络[4]、单周控制[5]以及模糊滑模控制[6]等，但非线性控制策略需要一个良好反映被控对象特性的模型，且计算复杂导致难以设计控制器。

本文提出一种新的功率变换器控制方法。通过使用NARMAX(Nonlinear Autoregressive Moving Average with Exogenous Inputs)模型(因为它是一种广泛使用的离散模型形式，并且具有一种简单的形式)完成功率变换器的辨识，但是这种模型不容易设计控制器，而U模型是一类光滑非线性对象时变参数的多项式函数，U模型在线性控制系统的设计方法与非线性动态系统之间搭建了一座桥梁，可以方便地用线性控制系统设计方法对非线性控制系统进行设计[7-8]。U模型覆盖了几乎所有现存的光滑非线性离散时间模型作为子集且易于设计控制器。所以，将NARMAX模型转化为U模型并基于U模型进行控制器设计，可在不损失非线性模型的任何特性下，简化了控制器的计算复杂性。目前U模型已得到充分的应用，文献[9]将U模型应用于电励磁同步电机并基于U模型设计了自抗扰控制器，文献[10]将U模型应用于直流电机并基于U模型设计了内模控制器。

本文通过辨识技术得到了Buck变换器的ARX(Autoregressive Exogenous)模型和NARMAX模型，并对这两个模型进行了有效性验证；然后，引入了U模型，将NARMAX模型转换为U模型并基于U模型设计了Buck变换器的极点配置控制器；最后，通过Simulink仿真分析与传统的PID控制器比较，验证了所提出方法的有效性。

1 模型辨识及有效性验证

首先利用ARX模型进行建模，然后通过交叉相关函数寻找NARMAX模型的缺失项。系统模型为

y(k)+a1y(k-1)+…+anay(k-na)=b1u(k-1)+…+
bnbu(k-nb)+ζ(k)

(1)

式中，u(k)和y(k)分别为系统输入和系统输出的采样观测值。首先选择ARX模型进行建模是因为ARX模型可以使用最小二乘(LS)算法直接估计。使p=1+max(na+nb)，其中na、nb分别为系统输出和系统输入的最大滞后，则式(1)可以写成如下形式:

y=[y(p),y(p+1),…,y(N)]T
θ=[a1,a2,…,ana,b1,b2,…,bnb]T
ζ(k)=[ζ(p),ζ(p+1),…,ζ(N)]T
x(k)=[-y(k-1),…,-y(k-na),u(k-1),…,u(k-nb)]

(2)

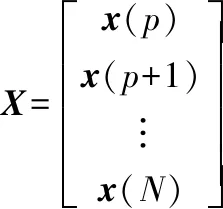
(3)

对于N个输入输出集，ARX模型可以用矩阵形式表示为

y=Xθ+ζ

(4)

进行矩阵变换后，最小二乘估计由式(5)给出:

(5)

如果残差序列ζ(k)是零均值白噪声，则式(5)中的估计是无偏的，那么预测模型与实际系统的接近程度可以用极小化误差平方和准则函数衡量。

(6)

在本仿真中，设置na和nb为2，使用最小二乘法计算参数，ζ(k)为残余误差。

y(k)=1.9843y(k-1)-0.9862y(k-2)+

0.0361u(k-1)+0.0734u(k-2)+ζ(k)

(7)

使用1000组数据对模型进行仿真后(900组数据用作辨识，100组数据用作有效性验证)，结果如图1所示。

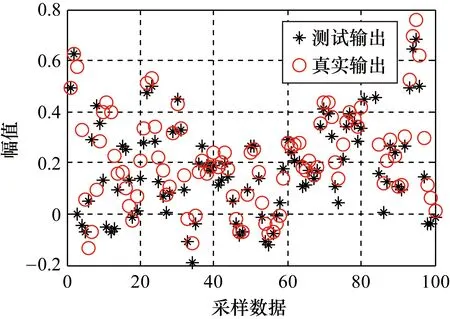
图1 ARX模型

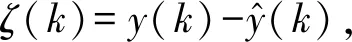
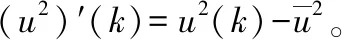
(8)

(9)

在相关性测试结果中，横坐标为时间延迟，纵坐标为相关性程度。图2为式(8)对ARX模型的4个测试。

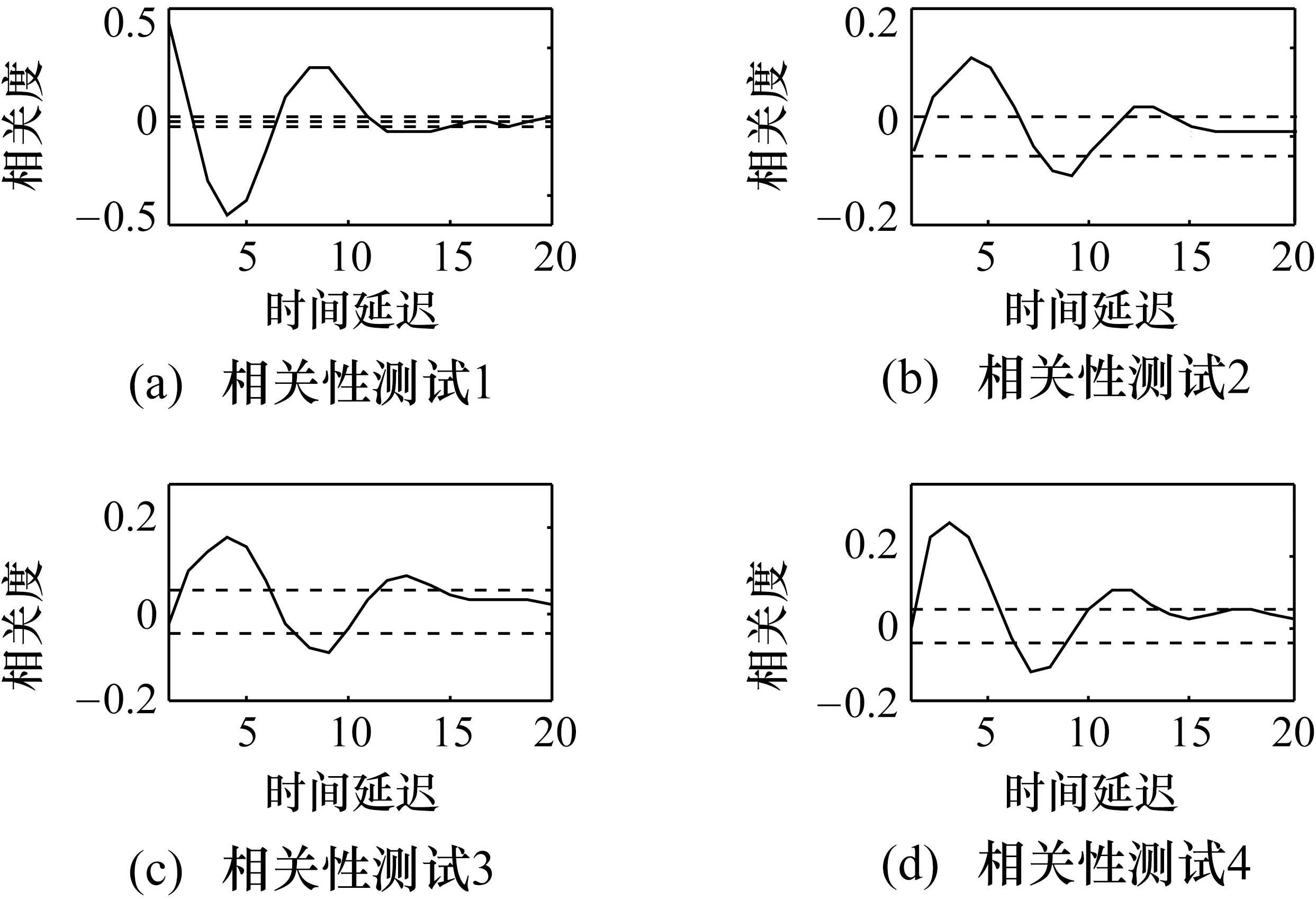
图2 ARX模型的相关性测试

从图2中可以清楚地看到这些测试是不合格的，各相关度均超出置信区间。这意味着残余项可能包含u(k-i)、u2(k-i)、u(k-i)y(k-i)。通过以上的分析，选择使用NARMAX模型，其定义为：

y(k)=F[y(k-1),…,y(k-ny),u(k-d),u(k-d-1),
…,u(k-d-nu),e(k-1),…e(k-ne)]+ξ(k)

(10)

式中，u(k)，y(k)和e(k)分别为系统输入、系统输出和噪声；ny，nu，ne分别为系统输出、系统输入以及噪声的最大滞后；d为时间延迟通常设置为1；F[·]为某个非线性函数。该模型实质上是对过去输入、过去输出以及噪声项的扩展。经过仔细分析，可以看出相比于ARX模型，NARMAX模型与非线性项相结合，极大地提高了识别复杂模型的能力。

使用的NARMAX模型结构如下：

y(k)=a1y(k-1)+a2y(k-2)+b1u(k-1)+

b2u(k-2)+cu(k-3)+du2(k-1)+

fu(k-1)y(k-1)

(11)

对比表明，该模型是基于ARX模型加上cu(k-3)+du2(k-1)+fu(k-1)y(k-2)。容易看到，尽管项cu(k-3)、du2(k-1)和fu(k-1)y(k-2)是非线性的，但是相较于整个NARMAX模型，如果把它看作一个整体项，则从参数辨识的角度来看，模型是线性的。所以，仍然能使用最小二乘法解决，其原理与上述相同。

仍然使用900组数据进行辨识，使用100组数据进行模型的有效性验证，结果如图3所示。

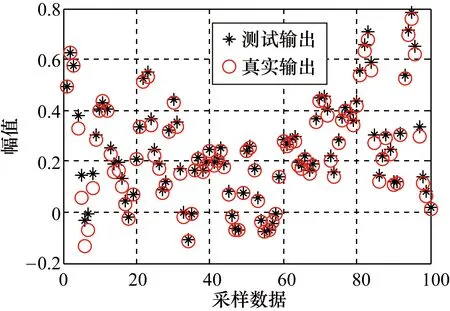
图3 NARMAX模型

y(k)=1.9721y(k-1)-0.9746y(k-2)+

0.0186u(k-1)+0.0747u(k-2)+

0.0373u(k-3)-0.0186u2(k-1)+

0.0238u(k-1)y(k-2)

(12)

从图3可以看出，选择的NARMAX模型输出能有效地跟踪真实输出。该模型中，J=0.0532，与ARX模型相同，NARMAX模型相关性分析如图4所示。

显然从图4中可以看出，NARMAX模型的相关性测试是合格的，即NARMAX模型可以很好地看作一个黑箱机理模型，并表达输出和输入的关系。因此在第2节中，将使用该模型转换为U模型来观察其控制效果。

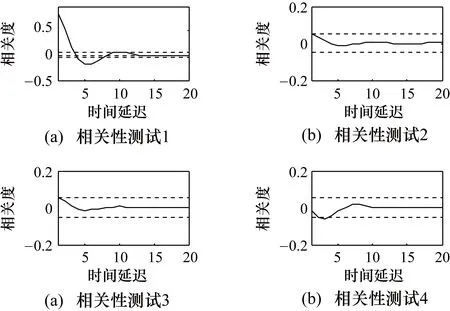
图4 NARMAX模型的相关性测试

2 基于U模型的Buck变换器控制器设计

面向控制的U模型可以通过扩展非线性函数f(·)关于u(k-1)的多项式获得，通过将非线性函数f(·)展开成关于u(k-1)的多项式，可以得到如下所示的面向控制的U模型。

(13)

式中，M为模型输入u(k-1)的阶；参数αj(k-1)为过去输入u(k-1)，…，u(k-n)和过去输出y(k-1)，…，y(k-n)以及过去误差e(k-1)，…，e(k-n)的函数。通过安排，面向控制的模型可以看作输入u(k-1)和相关的时变参数αj(k-1)的纯幂级数。方程(13)的表达式定义为U模型。换句话说，这是一个伪输入多项式闭合非线性模型。

根据上文对U模型的描述，Buck变换器的NARMAX模型可以变换成如下U模型：

(14)

基于U模型的极点配置设计使用了负反馈原理，控制器的输入信号由期望输出与实际输出过去时刻相关值比较得到，以此将极点配置到指定的位置。控制器输出由求解数学方程得到，并且通过对带有u(k-1)的多项式的模型结构进行有效性分析就完成了控制系统的设计，这大大简化了控制器的设计过程。当得到面向控制的模型时，使用一个标准参考形成以下公式来设计极点配置控制器，考虑方程(13)的U模型，极点配置控制器可以描述为

RU(k)=Tw(k)-Sy(k)

(15)

式中，w(k)为参考的输出信号；R、S、T为前移算子q的多项式，如下所示：

(16)

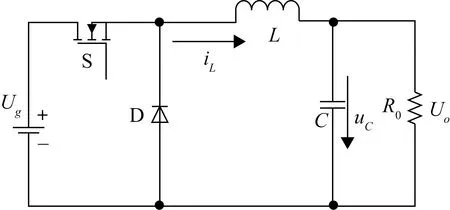
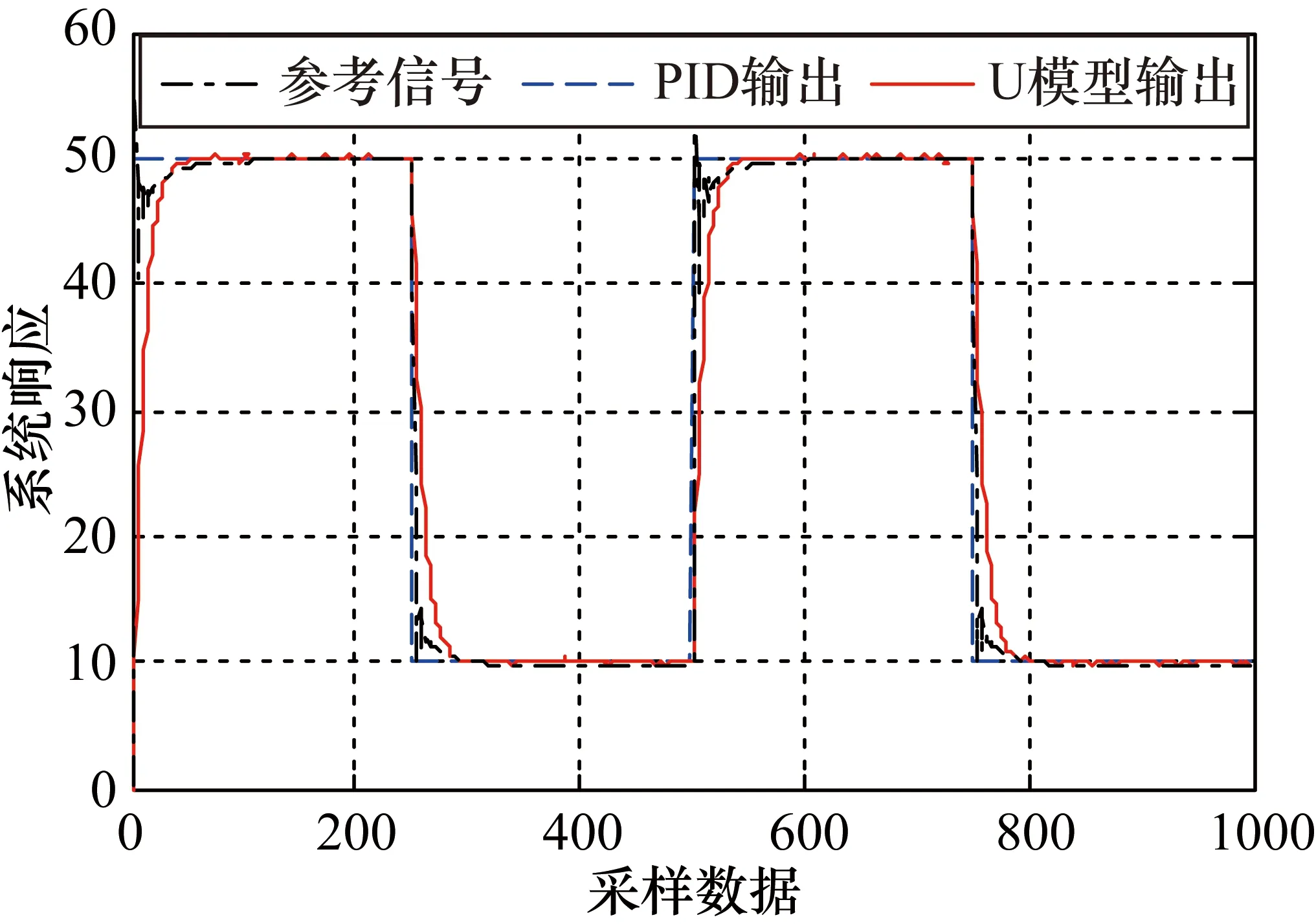
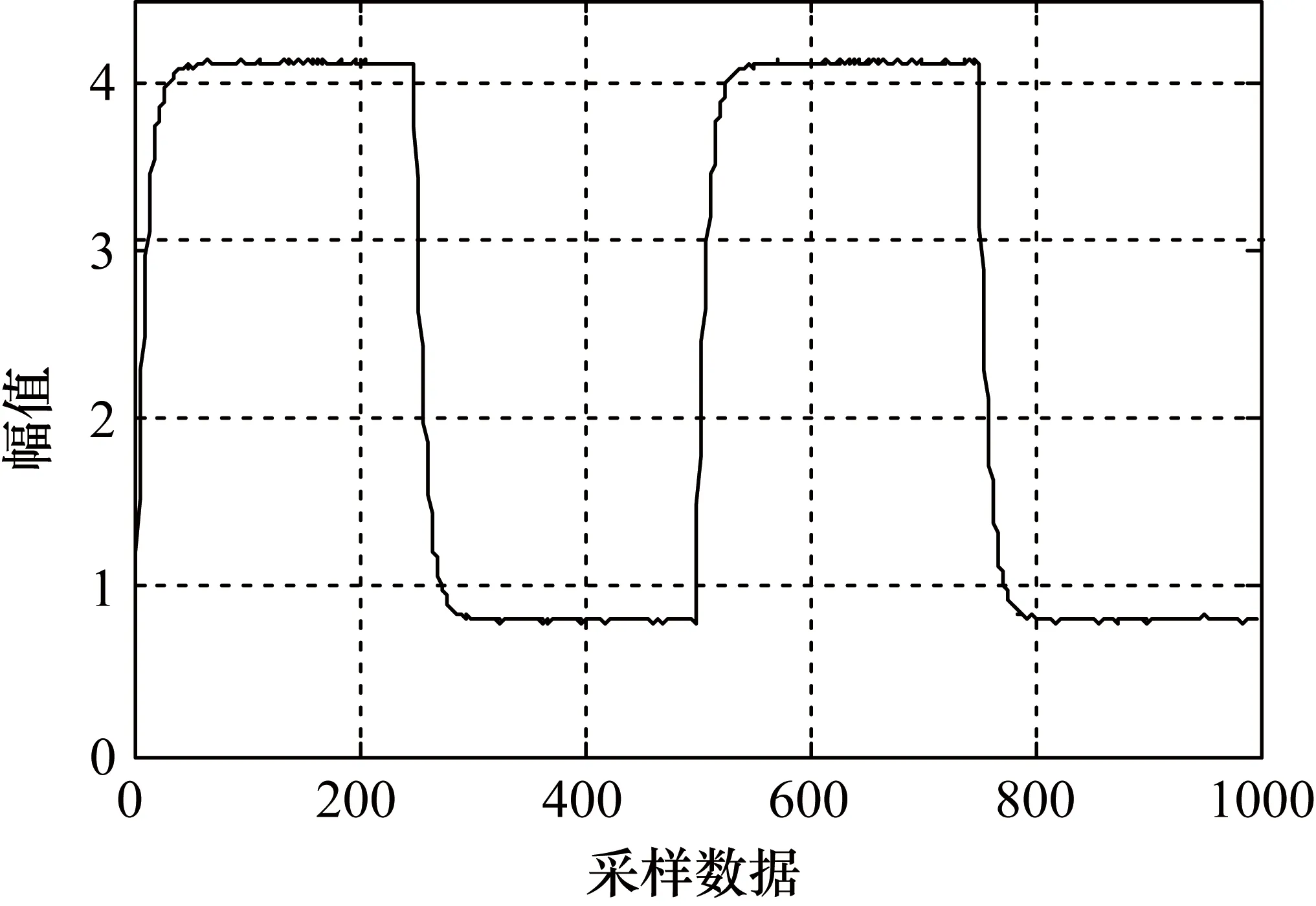
式中，q为前向算子；n、m、l分别为多项式R、T、S的阶。设计的控制器必须满足以下因果关系条件：l

方程的控制律表示一个传递函数为-S/R的负反馈和一个传递函数为T/R的前馈。所以其含有2个自由度。闭环控制系统的结构图如图5所示。实际输出y(k)可以与参考输出w(k)相联系：

(17)

图5 广义闭环非线性控制系统

多项式Ac为由设计者提前指定的闭环特征方程。为了消除作用在控制输出上的稳态偏移，在控制输出时使稳态误差等于零，指定多项式T为：

T=Ac(1)

(18)

极点配置设置的核心是指定期望的闭环特征多项式Ac。只要Ac确定，多项式T就确定，然后通过丢图番方程求解多项式R和S，3个多项式确定后，信号U(k)就可以通过方程(15)获得。

以U(k)作为根求解器，可以使用文献[9]中的牛顿拉夫逊算法找到控制器输出u(k-1)。递推计算描述如下：

(19)

式中，下标h为迭代指数，即第h+1次迭代从第h次迭代获得，h≥ 0。

本文中闭环特征方程指定为

Ac=q2-1.5q+0.609

(20)

得到闭环极点为0.75±0.216i，对应的无阻尼自然频率为0.96 rad/s，阻尼比为0.78。为了获得零稳态误差，指定

T=Ac(1)=1-1.5+0.609=0.109

(21)

对于多项式R和S，指定为

R=q2+r1q+r2,S=s0q+s1

(22)

将式(20)和式(22)代入丢图番方程R+S=Ac，多项式R和S中的系数可以表示为

r2+s1=0.609,r1+s0=-1.5

(23)

为了保证序列U(k)的计算收敛性，令r1=-0.9,r2=0.009。这样的安排对应U(k)的特征方程为(q-0.89)(q-0.01)=0。则S的系数可以通过多项式方程(23)中的丢图番方程确定为：s0=-0.6，s1=0.6。

将多项式R和S的系数带入到控制器方程(15)中，得到

U(k+1)=0.9U(k)-0.009U(k-1)+0.109w(k-1)+

0.6y(k)-0.6y(k-1)

(24)

则控制器输出u(k)可以用方程(19)求解得到。

3 仿真分析

首先在Simulink中搭建Buck变换器的模型，电路拓扑如图6所示。主电路由MOSFET管S、滤波电感L、滤波电容C、续流二极管D和负载电阻R构成。

图6 Buck变换器电路拓扑

首先，设计实验并进行数据预处理。选取占空比d=0.3作为系统的稳定工作点，采取零均值化方法进行数据预处理，通过在系统的稳定工作点上叠加零均值的输入信号M序列进行零均值化。辨识的输出信号为输出电压的变化量(M序列叠加稳定工作点下的输出电压减去稳定工作点下的输出电压)，辨识的输入信号为输入电压的变化量即M序列。值得注意的是，在整个工作过程中开关频率1/T=50 kHz保证了Buck变换器工作在连续工作模式下，即滤波电感上的电流不会为零。

接着，使用最小二乘法建立Buck变换器的ARX模型并进行相关性分析找出NARMAX的缺失项，将NARMAX模型转换成U模型进行极点配置控制器的设计。

最后，选择一个周期方波作为参考信号进行仿真，图7为参考信号为方波的系统反应，图8为参考信号为方波的控制器输出与三角波比较后得到的变换器输入信号。同时，选择PID控制方法作为对比，PID参数采用临界比例度法确定，效果如图7所示。

图7 方波的系统响应

图8 参考信号为方波的控制器输出

根据仿真结果，基于U模型的极点配置控制器在调节时间上优于传统PID控制法，且在超调量控制上具有显著优势。通过仿真实验可以看出，基于U模型的极点配置控制器控制效果较好，同时可以将线性控制系统设计方法扩展到Buck变换器的控制器设计中。

4 结论

通过一系列的测试和比较，可以看到对于状态空间平均模型，运用传统的PID控制方案在反应速度和反应精度方面效果不足。通过数据建模得到NARMAX模型，从而得到U模型并基于U模型设计控制器是一个可行的方法。

此外，在许多研究中，将先进控制技术与多种控制方法相结合，以获得更满意的控制效果。例如，U模型已经和预测控制、自适应内模控制等理论研究领域的控制方法相结合。利用U模型可以直接利用线性控制系统设计方法设计非线性控制系统控制器是一个可行的方法。所以，随着功率变换器控制技术的发展，基于模型辨识的控制方法，例如U模型控制，有更多的探索空间。