三维转动下旋转对称目标的转角估计方法

王超，叶春茂，文树梁

(北京无线电测量研究所，北京 100854)

0 引言

转角估计或者其等效的横向定标是逆合成孔径雷达(inverse synthetic aperture radar,ISAR)成像中的基本问题，受到了学者们的广泛讨论[1-2]。基于经典的距离—多普勒成像算法生成的ISAR像，其径向分辨率由雷达带宽决定，而横向分辨率主要由成像时间内目标的转角决定。通过转角的估计来完成ISAR图像的横向定标，可实现目标真实外形和尺寸等特征的提取，并为进一步的目标参数估计和分类识别提供基础。

传统的ISAR成像方法大多是针对转台目标模型提出的，此时目标将进行平面匀速旋转，对应的目标相对雷达的转角呈线性变化。相应的转角估计算法可以分为几类：①轨迹拟合法[3]。利用雷达的窄带跟踪数据，计算目标的飞行轨迹，进而估计目标相对雷达的转角变化。②特显点跟踪法[4]。通过跟踪目标上几个孤立的散射点，对其相位变化历程进行参数化拟合实现转角估计。③图像熵法[5]。对于不同转角下的ISAR图像，以评价函数为衡量，选取最优ISAR像对应的转角。同时，文献[6-7]通过在距离像序列的距离单元内对信号调频率进行估计，完成了成像积累角的估计。文献[8]将目标转动时不同距离单元回波数据近似为多分量3次相位信号，并采用最大似然方法估计3次相位信号参数实现最终的转角估计。

对于三维转动目标，其目标的姿态变化是高度非均匀的，对应的目标相对雷达的转角呈高度非线性变化。这为传统的转角估计算法的有效性带来了挑战，也对转角的精确估计造成了困难。针对此，文献[9]提出了一种基于图像配准的ISAR横向定标方法，通过设计仿射变换矩阵，将配准图像的仿射参数与横向比例尺相关联，完成最终的横向定标。本文在此基础上，证明了三维转动的旋转对称目标在径向距离—速度差平面上的旋转匹配特性。进而，基于该特性在视线角的二阶多项式模型下提出了一种转角估计算法。仿真实验以进动锥柱体为例，在一个进动周期上对等效转速进行估计，结果表明本文算法在几乎所有的成像时刻都能有效估计目标转角。实验还对不同散射点个数对转角估计性能的影响进行了分析。

1 旋转对称目标的三维转动模型

对于旋转对称目标，目标强散射区域体现为对称轴两端尖锐的顶锥或目标表面不连续处凸起或凹陷的圆环。因此，可用对称轴上的固定散射点和与对称轴垂直的圆环边缘处的滑动散射点对高频雷达观测下的旋转对称目标进行表征。以目标对称轴为y轴，雷达方向矢量所在平面为Oyz面，基于右手螺旋法则构建本体坐标系。图1给出了本体坐标系中相应的几何模型，其中，目标上可能出现的两类散射点分别用A(固定散射点)和X(滑动散射点)进行表征。基于文献[10]的分析，滑动散射点位于雷达方向矢量以及目标对称轴构成平面与圆环边缘的交点，因此滑动散射点X与雷达方向矢量nrad，目标对称轴nA共面。

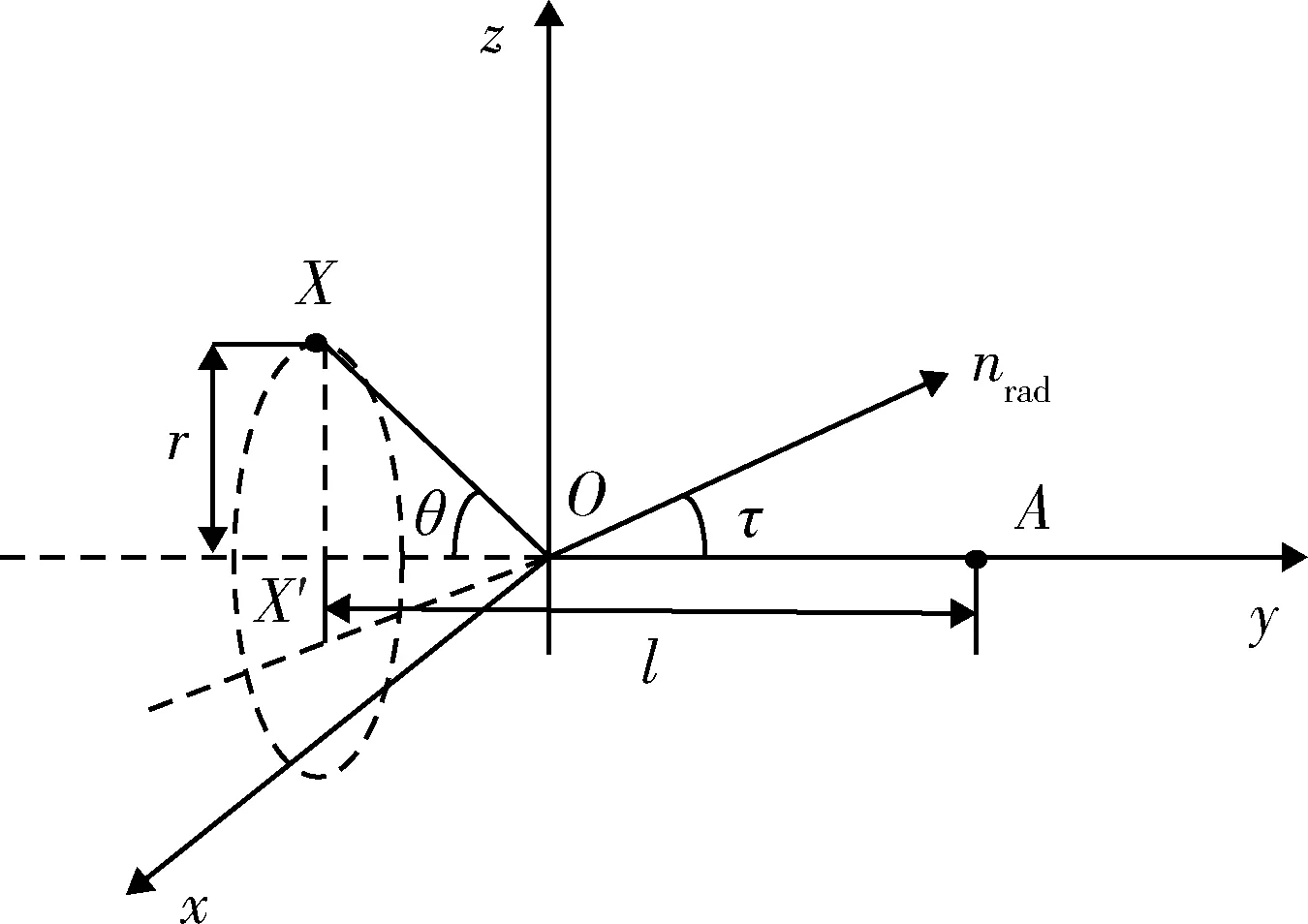
图1 旋转对称目标几何模型Fig.1 Geometric model of rotational symmetric target

由于微动分析常在参考坐标系中进行，当目标进行三维转动时，固定散射点位置可由旋转矩阵表征[11]：

(1)

基于Rodrigues公式，绕固定旋转轴旋转的旋转矩阵可近似为

(2)

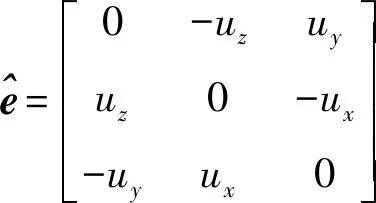
因此，对于包含n次旋转运动的三维转动目标，其三维转动旋转矩阵可表达为

Rrot(t)=Rr1(t)Rr2(t)…Rrn(t),

(3)

式中：Rri(t),i=1,2,…,n为各次旋转对应的旋转矩阵。

对于雷达远场观测下的旋转对称目标，由于其旋转对称性，可将这种三维转动与二维平面转动等价。换句话说，其运动特征可由一维的雷达视线角(目标对称轴和雷达视线矢量夹角)表征为

(4)

式中：τ(t)为瞬时雷达视线角。

假设平动被精确补偿，则固定散射点A对应的瞬时径向距离为

RA(t)=R0-OA(t)·nrad=

(5)

式中：R0为参考中心O相对雷达的参考距离。

瞬时径向速度为

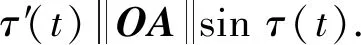
(6)

类似地，为简化表达，对于滑动散射点用统一符号X表示，由于其始终处于由对称轴和雷达方向矢量构成的平面上，因此，其瞬时径向距离可表达为

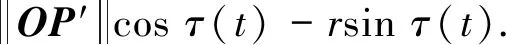
(7)

相应的瞬时径向速度为

rcosτ(t)).

(8)

2 基于旋转匹配特征的转角估计

在实际情况中，对于非合作目标参考距离通常是未知的，并且平动的精确补偿也是较难实现的。因此，在转速估计中，通常假定一个等效旋转中心，利用相对等效中心的径向距离和速度来忽略平动以及参考距离的影响。具体地，将A点视为等效旋转中心，可得相对径向距离

RAX(t)=-lcosτ(t)+rsinτ(t),

(9)

式中：l为目标的径向长度;r为滑动散射点所在圆环的半径。

进而可得相对径向速度为

-τ′(t)(lsinτ(t)+rcosτ(t)).

(10)

与二维平面转动相对应，这里定义雷达视线角变化率τ′(t)为三维转动的等效转速(equivalent rotation velocity,ERV)。基于式(9)和(10)的推导，可将两相邻时刻的相对径向距离和速度变换为矩阵形式:

(11)

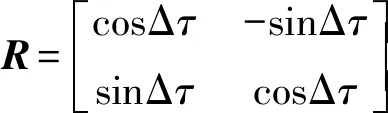
由于从雷达回波中仅能提取到径向距离和速度值，同时为了与光学图像的旋转匹配作区分，将式(11)改写为

(12)

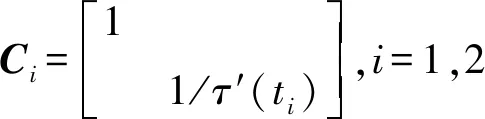
(13)

式(12)说明了三维转动下的旋转对称目标在径向距离—速度差平面上仍旧满足旋转匹配特征，因此，可以基于该特征利用图像旋转相关等方法实现转角估计。基于提取到的径向距离差和速度差，还需要确定的变量为两时刻视角差Δτ以及两时刻的ERVτ′(t1)和τ′(t2)。通过式(4)可发现，对于三维转动目标，其雷达视线角τ通常是呈高度非线性变化的。因此，为简化计算而又不失一般性，在相邻的两时刻内将视线角等效为二阶多项式模型

τ(t)≈τ(t1)+τ′(t1)(t-t1)+

(14)

于是，由两时刻ERV表征的视角差可表达为

(15)

进而，式(12)中的变量仅为两时刻的ERVτ′(t1)和τ′(t2)。因此，可基于匹配的最小误差准则，对ERV进行估计并基于式实现转角估计。具体的有

(16)

(17)

由于目标中可能包含多个强散射点(大于2个)，式(16)中径向距离差RAX和速度差vAX构成了距离—速度差平面上提取的多个强散射点的二维坐标矩阵。需要说明的是，坐标矩阵应预先完成两时刻间相同散射点的关联，关联方法可基于两时刻散射点坐标的最近邻准则。同时，为保证估计方法的有效性，需实现至少3个不在同一条直线上的点的有效提取与关联[12]，其中一个为锥顶点A，其余为边缘滑动散射点。若精细的散射点提取与关联难以实现，也可采用文献[13]给出的基于图像旋转的转角估计方法。

3 仿真校验

这里以进动的锥柱体为例，基于不同个数的散射点对所提的三维转动目标的转角估计方法给出验证和分析，具体几何结构图如图2所示。其中，参考中心O到锥顶点A的距离为1.2 m，O到锥柱体底面的距离为0.6 m，底面半径为0.3 m，转动角速度w=2π rad/s，目标主轴与旋转轴nr构成的进动角10°，雷达视线向量nrad与旋转轴nr构成的平均视线角160°。同时，假设雷达系统参数为雷达载频15 GHz，脉冲重复频率512 Hz，仿真时间1 s。基于不同视角下目标上散射点的可见度分析[14]，可发现当前视角下散射点A，B，C和C′是可见的。因此，下面将基于这4个可见散射点的径向距离和速度进行转角估计，同时对不同散射点个数下的估计性能进行分析。为了分析的方便，估计结果以各个时刻的ERV估值进行表征。

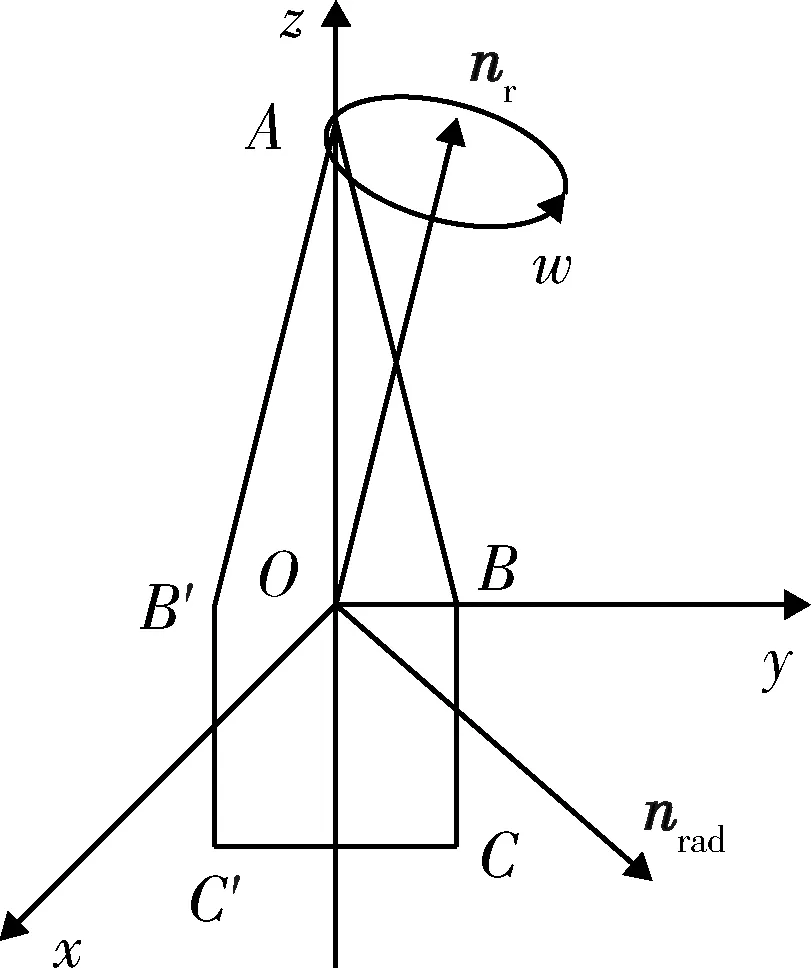
图2 进动锥柱体几何结构图Fig.2 Geometric model of conical cylinder with precession

对进动下的锥柱体目标进行理论分析[15]，可得到不同时刻的雷达视线角及其变化率，如图3所示。从图3中可以发现，不同于传统的转台目标，此时的雷达视线角具有高度的非线性。相应地，各散射点的径向距离和速度变化曲线示于图4中。同样可以看到，除了锥顶散射点A，其他各散射点曲线的变化趋势都偏离了正弦形式。这为三维转动目标的转角估计带来了新的挑战。同时，由于不同散射点径向距离和速度的在变化幅度和形式上的差异性，使得基于不同的散射点进行后续特征提取等工作的效果也将不同。

图5展示出了不同时刻图像的旋转匹配特性，图中散射点的分布为B，C和C′点相对A点的位置坐标，并基于理论ERV实现横向定标。图5中时刻1、时刻2以及时刻1旋转后的图像以不同的形状进行表示，其中，a)，b)，c)分别令初始时刻、第100次回波时刻、第200次回波时刻为时刻1，时刻2与时刻1相差30次回波。可以发现，时刻1旋转后的图像与时刻2图像基本吻合，与理论分析一致。同时，对于固定时间差的2幅图像，由于视角变化的非线性，对应的视角差(或者说2幅图像散射点在位置上的差异性)不同。特别是如图5b)中视角差较小的情况，转角估计性能将会下降。

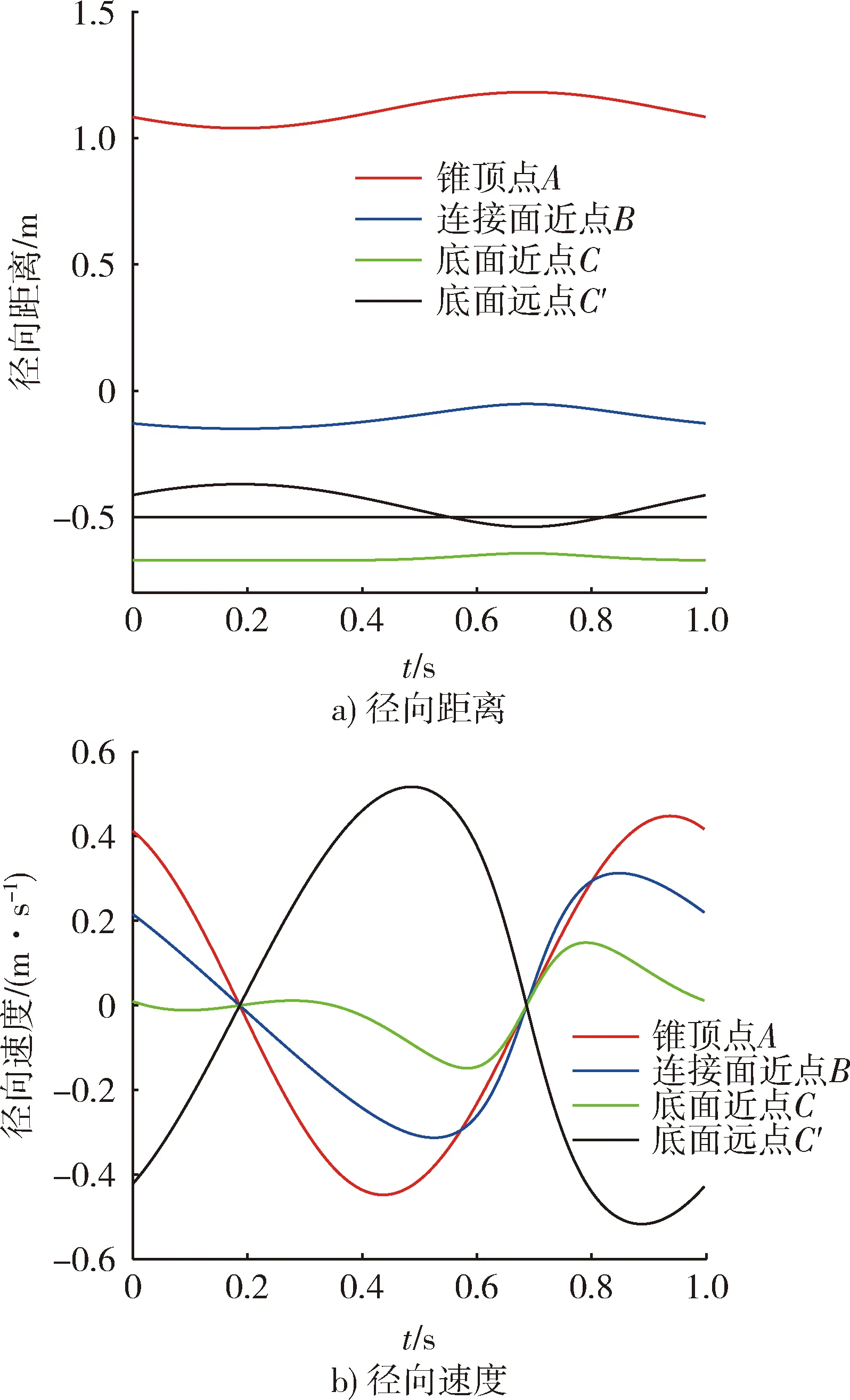
图4 径向距离和速度的提取结果Fig.4 Extraction result of radial range and velocity

为了分析散射点对后续转角估计的影响，这里分别利用①A，B，C和C′4散射点；②A，B和C3散射点；③A和B2散射点基于式对ERV进行估计，所得结果示于图6中。时刻1以10个回波为间隔步进，时刻2与时刻1恒定相差30个回波。同时，转速估计的结果是关于0点模糊的(即在0点两侧成对出现)，因此图6中将估计结果和理论值取绝对值后进行比较，而转速的去模糊则需要利用额外的信息和算法。可以发现，对于图6a)和b)中4散射点和3散射点的情况，几乎在整个周期上都能实现转角的有效估计。其中误差相对较大的几个时刻可能是由于视角差过小造成的。需要说明的是，由于实验中提取的径向距离和速度值较为理想，因此对于实际情况中存在误差的参数估计，使用更多的散射点数据将提高算法鲁棒性。而对于图6c)中2散射点的情况，由于不满足文献[12]中的假设，估计性能则明显变差并且出现了错误的估计点。

图5 不同时刻定标图像的旋转匹配特性Fig.5 Rotation matching feature of cross scaled ISAR images at different time

图6 基于不同个数散射点的转角估计性能Fig.6 Rotation angle estimation results based on different scattering points

4 结束语

针对三维转动的旋转对称目标转角估计问题，本文提出了一种基于旋转匹配特性的估计方法。首先证明了目标在径向距离—速度差平面上的旋转匹配关系，进而，基于雷达视线角的二阶多项式近似实现了转角的估计。仿真实验表明,本文算法在几乎整个周期的任意时刻都能有效估计目标转角。估计的转角可用于ISAR图像的横向定标以及后续的特征提取。而针对基于非固定间隔图像和不同视线角近似模型的估计算法将成为后续工作重点。