数学美在高中数学中的展现

周伟.茶陵县第二中学.湖南株洲.412400

数学家普罗克拉斯断言：“哪里有数，哪里就有美。”很多学生厌倦数学，认为数学是一门只是计算、枯燥、乏味的学科，甚至有人闻‘数’丧胆。在数学教学过程中，我们教师要通过对数学美的分析和挖掘，充分让学生感受到数学中固有的数学之美，提高学生对数学美的认识，引发他们对数学学习的兴趣。在自己从事高中数学教学的工作中，我对数学美有这几点发现：

一.数学美之符号美

符号是某种事物的记号，数学符号也作为符号的一种，它指把原本繁琐的文字语言用系统的符号表示出来，实现了数学的形式化。数学符号可以分为哪几类呢？

1.（1）标识符号：通常是约定的或对字母的变形获得的特殊记号,如等；（2）标点符号：借用一般标点符号的形式,表示不同的意义。如（），{}，等；（3）字母符号：主要取自于某种语言的字母或文字。如圆周率π，体积V等；（4）象形符号：常用直观图形演变而来，多数用于几何。如：Δ，‖等；

2.（1）数量符号：表示数量的数学符号。如： e,π,i,等；（2）运算符号：表示数学运算的数学符号。如.Y，等；（3）结合符号：表示运算关系顺序的数学符号。如{}，[],()等；（4）性质符号：表示数学对象的性质符号。如+，-，|x| 等；

3.（1）元素符号：表示数与几何图形的符号。如1，2，ι，α，λ，等；（2）辅助符号：为了方便表达和计算,数学里还引进了某些符号用于表示特定的式子或者某种特定的意义。如根的判别式Δ，三角形全等符号（sss)等；（4）关系符号：表示数、式、形之间关系的符号。如等；

由此可见，数学符号不但可以使数学内容结构简洁明了，更展示了数学在形式上的独特魅力。

二.数学美之公式美

在现行中学统编教材中，数学公式至少有500个，如同人体骨头一般搭起数学知识的框架，围绕它们展开一系列的证明、应用，构成了多姿多趣的数学。重视数学公式的教学，对学生的学习起着相当大的影响。

欧拉公式被称为“最美数学公式”eiθ=cosθ+isinθ，它将指数函数、三角函数和复数的知识完美地结合在一起。式中的5个常数都是自然科学中非常重要的常数，在数学中有其深刻的含义。尤其是θ=π时，可得eiθ+1=0，即eiθ=-1，这一重大发现标志着数学发展的两个重要阶段--数的概念由正数延展到负数,由实数延展到虚数，同时，我们可以得到ei=(2.718281828……)-1，这是置身于实数域中的人无论如何也难以想象的。

三.数学美之图形美

在数学这门学科中，图形占据着一个重要的地位。函数图象、平面几何、空间几何等。如空间立体图形是需要一定的想象能力才可以想象出来的。如图是我们常见的立体图形--圆柱。

通过图象，我们发觉，圆柱是由三个面组成的，分别是底面、侧面、底面；且两个底面是圆，侧面是一个矩形。根据圆柱展开图，我们可以得出圆柱的表面积、侧面积、底面积、体积等公式，而且可以得出圆柱的三视图。

通过对圆柱图象的认识，让学生知道了圆柱的立体构成，也掌握了圆柱中的有关计算公式及三视图，也让学生体会到立体几何图形的美。

四.数学美之内容美

在数学中，许多数学内容也是特别美的。如：杨辉三角、勾股定理、斐波那契数列、黄金分割比等。

著名的杨辉三角是蕴藏着组合恒等式的宝库，有许多规律。

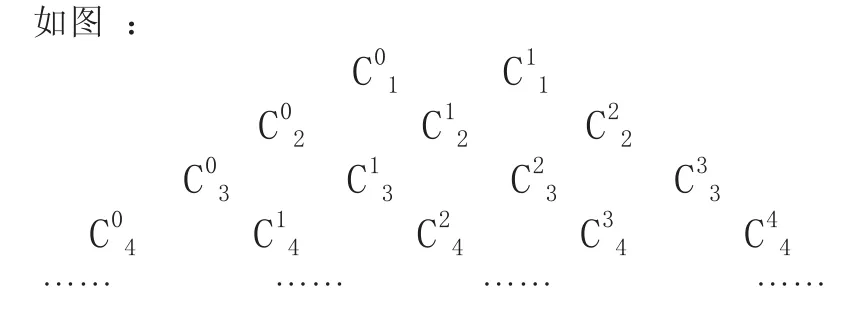
又如：著名的斐波那契数列

1,1,2,3,5,8,13,21,34,55,89,144,LL它具有以下几个特征：

（1）除开头两个1以后的每个数字都是由前面两个数字相加而得。如：1+1=2，2+1=3，3+2=5，5+3=8等；

（2）除起始几个数字外，任何一个数字为前面第二个的2.618倍。如：34÷13=2.618，55÷21=2.618，89÷34=2.618等；

（3）除起始几个数字外，任何一个数字为前面一个数字的倍。如：21÷13=1.618，34÷21=2.618，55÷34=1.618 等；

通过对斐波那契数列的研究，找到了数字的内在规律，感受到数学美的特性。

总之，数学美无处不在，数学本身处处充满了美的韵律。挖掘数学美，传授数学美，是新课标背景下的教师必须具备的教学技能，引导学生理解数学美、欣赏数学美，才能全面地理解数学的本质，培养学生的积极性。