基于主动加热光纤法的冻土相变温度场特征分析*
吴 冰 朱鸿鹄② 曹鼎峰 王家琛 魏广庆 施 斌
( ①南京大学地球科学与工程学院 南京 210023)
( ②中国科学院西北生态环境资源研究院冻土工程国家重点实验室 兰州 730000)
( ③中山大学土木工程学院 广州 519082)
( ④苏州南智传感科技有限公司 苏州 215123)
0 引 言
冻土是一种温度在0 ℃或0 ℃以下、含有冰的岩石和土壤,强烈的温度敏感性是冻土区别于其他土壤介质的重要因素( 马巍等,2014) 。冻土地区工程建设首先需要考虑冻土地基的热稳定性,预估地下土层的温度场分布。准确获取导热系数、体积热容量和相变潜热等冻土热物理性质参数是开展地层温度场分析和评价的前提条件( 胡田飞,2015) 。
土壤热物性参数的常规测试方法分为稳态法和瞬态法( 尹飞,2008; 郑志涛,2013) 。后者在测量时间、成本和可移植性方面都优于前者( He et al.,2008) 。线热源法是瞬态法的一种,具有测量快速、操作简单的优点,在工程中得到了广泛的应用( 杨杰,2014) 。
与其他传感器相比,光纤传感器具有体积小、灵敏度高、抗电磁干扰、耐化学腐蚀、可远程和分布式测量等优势,在地质与岩土工程监测领域有着巨大的应用潜力( Fang et al.,2012; 施斌,2017; Joe et al.,2018; 周谷宇等,2018; 施斌等,2019) 。主动加热光纤( AHFO) 法是一种基于线热源模型的光纤感测方法( Weiss,2003; Sayde et al.,2010; 曹鼎峰等,2014; Duminda et al.,2018) 。该方法将分布式温度传感( DTS) 技术与传统线热源探针相结合,在保护光纤的护套或管体中通电加热产生热脉冲,光纤作为温度传感器测量土壤的热响应,通过建立温度变化与热物性参数之间的关系实现参数测量。国内外一系列室内和原位试验表明,AHFO 技术可以在高时空分辨率下表征土壤热导率和土壤水分动力学特征( Ciocca et al.,2012; Cao et al.,2015; 严珺凡等,2015; 曹鼎峰等,2018) 。
然而,冻土独特的温度敏感性造成其传热问题的特殊性和复杂性( 史金艳等,1988; 何瑞霞等,2018) 。目前将AHFO 技术应用于冻土监测时,通常未考虑冰水相变问题,因此得到的线热源温度场解析解误差较大,难以精确计算冻土热物性参数。尤其是在冻土近相变区,剧烈相变使测量结果严重失真,线热源模型的传统分析方法不再适用。如何在考虑冰水相变的情况下提高AHFO 法的测量精度,是一个亟待解决的问题。
本文将自主研发的FBG 刚玉管传感器同时作为线热源和温度传感器,基于AHFO 法开展了一系列室内试验,对冻土温度场的分布特征进行了监测和分析; 在考虑未冻水和相变潜热的情况下,通过理论公式和试验数据,计算、反演出冻土的导热系数和相变热容,并验证分析了它们与测量初始温度之间的关系。相关结论为基于AHFO 的冻土含冰量测量方法的修正提供了参考依据和理论支撑。
1 理论方法
1.1 冻土热传导方程
热量在土壤中主要有传导、对流和辐射3 种传输方式,其中辐射和对流只有在大孔隙、高温差或者土中有水分渗流时才考虑,在黏性土中可以忽略不计( 徐斅祖等,2001) 。
在基于AHFO 的冻土含冰量测量过程中,线热源工作将引起冰水相变,产生的相变潜热以内热源的形式影响冻土热传导。包含相变热容的冻土一维热传导控制方程可以表示为( Liu et al.,2011) :
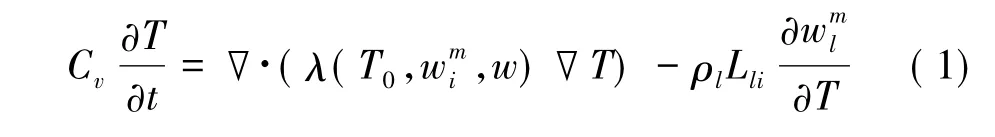
式中,T0和T 分别为土体初始温度和温度; ρl为水的密度; Lli为冰水相变潜热,即单位质量水冻结成冰释放的热量,取值为334.3 kJ·kg-1; w 为总含水量;和分别为土体含冰量和未冻水含量; λ 为土体导热系数,对于同种类型的土体,λ 受和w 控制; Cv为体积热容。
在线热源模型中,线热源温度增量与周围土体导热系数关系为( Weiss,2003) :
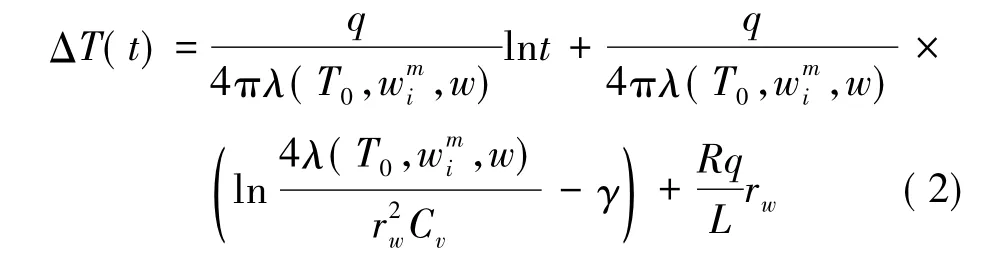
式中,t 为加热时间; q 为单位长度热源的放热功率;rw和L 分别为刚玉管半径和长度; R 为管体与钻孔壁面之间的热阻; γ 为欧拉常数,取0.577 216。
采用线性推导法对导热系数λ 进行估算,将式( 2) 简化为温度变化ΔT( t) 与时间对数lnt 的线性关系,令其斜率为m,则冻土导热系数为:
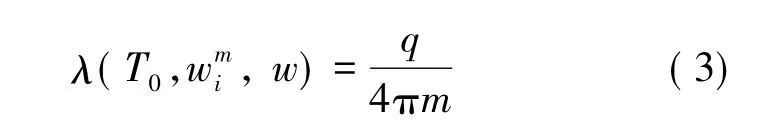
在基于显热容法的冻土导热系数与温度关系的分析中,λ 与T 的关系如下式所示( 林文生,2007) :

式中,f、d 分别为与冻土相变温度有关的常数。
冻土体积热容Cv由冻土的组成成分及含量控制,可表达为( 张喜发等,2013) :
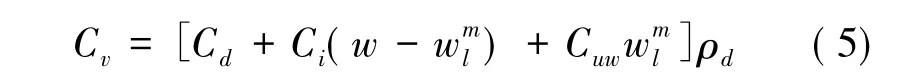
式中,Cd、Cuw和Ci分别为土颗粒、未冻水和冰的比热; ρd为土壤干密度。
根据大量研究,未冻水含量wml 与土质类别和温度相关,黏土未冻水含量的经验公式为( 张喜发等,2013) :
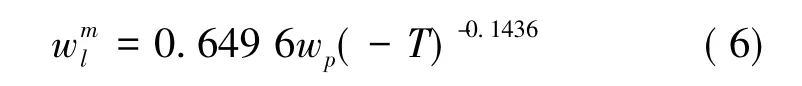
式中,wp为土体的塑限。
为区别于体积热容,定义相变热容CL为( 周家作等,2016) :
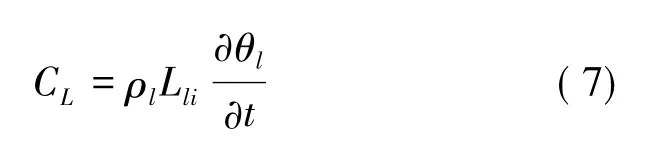
相变热容和体积热容之和为表观热容,即:

结合式( 1) 、式( 5) 、式( 7) 、式( 8) ,就可以得到包含相变的冻土热传导方程,将其转化为极坐标形式:
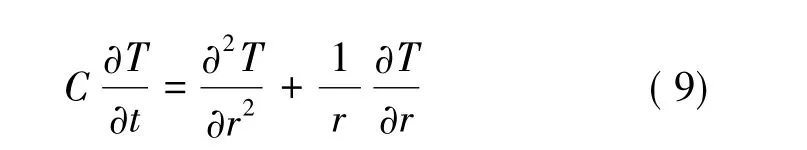
由式( 9) 可以得到加热t 时刻距离热源半径r处土体的温度增量分布解答:
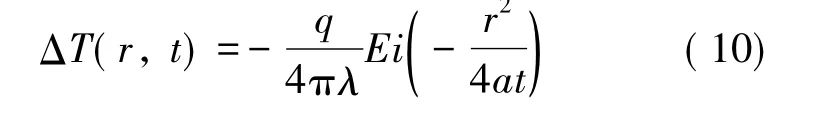
式中,Ei 为指数积分函数; a 为冻土导温系数,是导热系数与热容的比值。
经过国内外学者的大量研究,上述原理在理论上已经十分成熟。但是对于冻土热传导而言,式( 1) 中最后一项相变潜热项为该技术的应用增大了难度。
首先,主动加热法测量冻土导热系数过程中,会出现两个问题: ( 1) 土体升温必然会使得在测量过程中导热系数是一个变量,是否可以将其当作定值进行简化计算? ( 2) 如果问题一是肯定的,那么导热系数简化值与不同土体初始温度之间是否仍为线性关系? 其次,式( 7) 得到的相变热容并不是一个常数,且无法通过解析解直接计算。那么如何才能得到相变热容,以及其随土体初始温度的变化规律呢? 本文通过一系列室内试验来探究这一问题。
1.2 基于导热系数与初始温度线性关系的含冰量测量方法修正
最近,基于FBG 刚玉管传感器的土壤含水量和含冰量测试方法相继被成功研发( 段超喆等,2018) ,并应用于甘肃会宁等地的原位监测中。在监测冻土含冰量时,该方法存在一定的局限性:该方法是在极低温度下( -20 ℃) ,将含冰量作为单一因素为前提而实现的。但是在实际情况下,冻土温度与大气温度有关,且即使在很低温度下冻土中依然会存在未冻水。
本文在考虑未冻水和冻土初始温度的情况下,基于1.1 中导热系数与初始温度之间的线性关系,对基于FBG 的冻土含冰量测量方法进行修正。
在考虑未冻水的情况下冻土导热系数为:

式中,A、B、C 为与土体性质有关的常数。
依据式( 2) 、式( 4) ,冻土导热系数与初始负温呈线性关系,则传感器所得温度增量ΔT( t) 与lnt 的关系曲线斜率m 与初始负温关系呈负相关关系,可表示为:
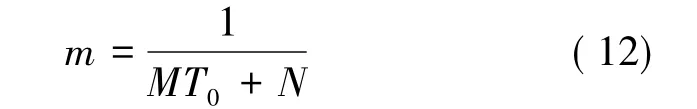
依据式( 11) 、式( 12) ,将其代入含冰量测量的理论推导过程中可得:
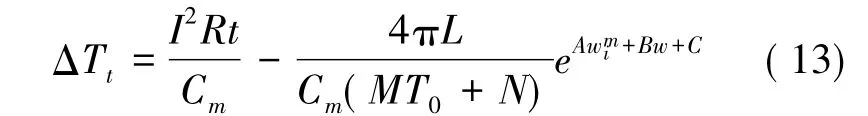
式( 13) 可简化为:
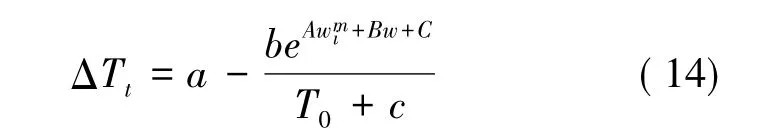
式( 14) 表明,传感器所测温度特征值与含冰量、总含水量之间为指数关系,与初始负温之间为倒数相关关系。上式不仅可以应用于含冰量的测量,在常温下不考虑变量T0也可以拓展到土壤含水量的测量。A、B、C、a、b、c 的确定可以通过室内标定试验实现。
2 试验装置与方法
本文中试验研究的目的是,将AHFO 法应用于冻土热物性参数以及含冰量测量中,分析初始含水量恒定的冻土在不同温度下的热响应特征,探究验证导热系数、相变热容与冻土初始温度之间的关系,并基于分析结果对冻土含冰量测量的修正方法进行验证、评价。
试验装置如图1 和图2 所示,由环刀试样、FBG刚玉管传感器、数据采集系统、热敏测温系统和直流稳压电源组成。试验土样为南京地区的典型下蜀土,经过压制成为圆柱形环刀样; 为消除主动加热过程中边界效应的影响,试验选取直径100 mm、高度63.7 mm 的环刀。试验中采用同时具有内加热和测温功能的FBG 刚玉管传感器,其外径为4 mm,内孔径为1 mm,有效长度40 mm。管体内置温度传感光纤和阻值为28 Ω·m-1的加热电阻丝。数据采集系统由苏州南智传感科技有限公司生产的A-01型FBG 解调仪和计算机组成,用于实时读取刚玉管传感器的波长数据。热敏测温系统由RC-4 型高精度温湿度记录仪和不锈钢热敏探针构成,用于测量和记录加热t 时刻半径r 处的温度信息。
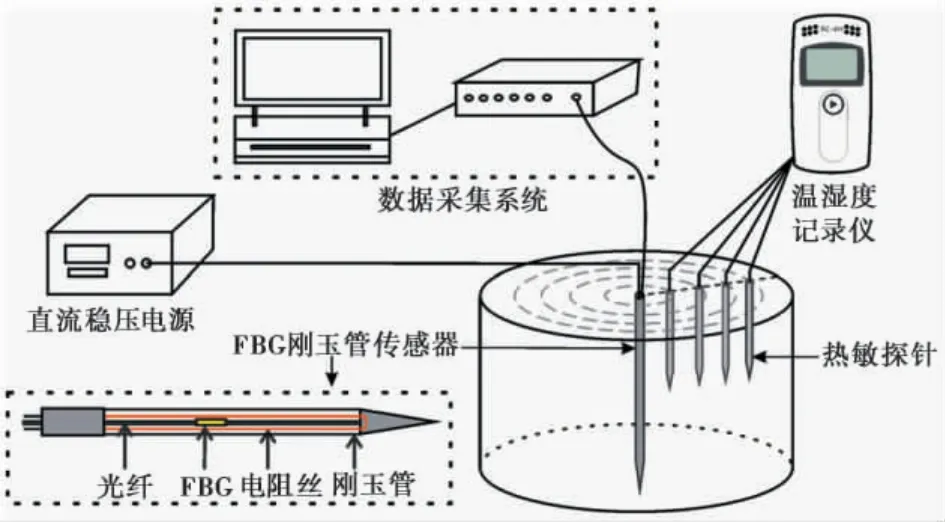
图1 试验装置图Fig. 1 Schematic diagram of the test setup

图2 试验装置实物图Fig. 2 Photograph of the test setup
FBG 刚玉管传感器布设在环刀试样正中心轴线位置,与周围土体保持良好的接触性,并与直流稳压电源和光纤解调仪连接。不锈钢热敏探针分别布设在径向距离轴心1 cm、2 cm、3 cm 和4 cm 处。试验过程中土样连同刚玉管传感器和不锈钢温度探针用聚乙烯薄膜密封后放置于低温箱中,直流电源、解调仪和温湿度记录仪置于室内常温中。
试验中控制土样干密度为1.63 g·cm-3,初始含水量为20%,土样的初始温度依次为21.9 ℃( 室内常温) 、-0.6 ℃、-3.2 ℃、-6.7 ℃、- 11.9 ℃和-20.6 ℃。为了达到温度均匀,土样在每个温度下恒温12 h 以上。然后,在相同加热功率下对冻土试样中的传感器进行主动加热,测量不同初始温度下土样的温度变化情况。试验过程中,FBG 刚玉管传感器的加热功率设置为23 W·m-1,加热时间为300 s,FBG 解调仪和温度记录仪分别以1 s 和10 s的采样间隔记录温度测值。
3 结果与讨论
3.1 导热系数与初始负温的关系
根据试验中FBG 刚玉管传感器的监测结果,可以得到不同初始温度下传感器管体温度增量ΔT( t)与加热时间对数lnt 的关系曲线( 图3) 。由于加热初始阶段产生的热量主要用于传感器管体升温,不符合线热源模型,因此仅考虑加热后40~300 s 的温度信息。由图3 可以看出,在加热40 ~300 s 期间,ΔT 与lnt 保持良好的线性增长关系。这说明在冻土升温过程中,土体温度变化引起的导热系数的变化幅度较小,可以忽略不计。因此在本文所述试验条件下,可以将冻土导热系数当作定值以进行简化计算。
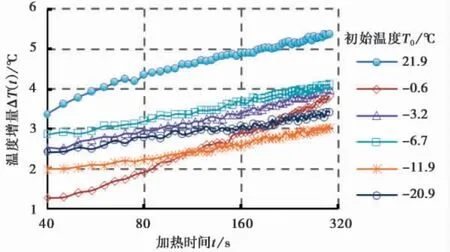
图3 温度增量与时间关系曲线Fig. 3 Curves of ΔT( t) and t
对图3 所示曲线进行线性拟合,所得ΔT( t) 与lnt 曲线的斜率为m,根据式( 3) 可得不同初始温度下冻土的导热系数。由图4 可以看出,试样在室内常温中导热系数λ0=2.2 W·( m·K)-1。在初始温度低于-3.2 ℃时,导热系数均大于λ0,且随温度升高呈线性减小趋势。这是因为在初始含水量一定时,土体导热系数取决于含冰量和未冻水含量。常温条件下未冻水含量= w; 随温度降低,冻土含冰量增加,未冻水含量减少,而冰的导热系数约为未冻水的4 倍,所以冻土的导热系数随初始温度降低、含冰量增加而增大。
基于最小二乘法可以得到该温度区间冻土导热系数与初始温度的线性关系曲线,且拟合度很高。
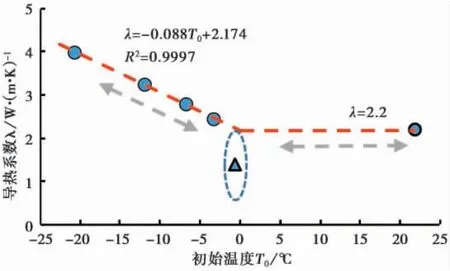
图4 导热系数随初始温度变化曲线Fig. 4 Relationship between thermal conductivity and initial temperature
此结果表明,在一定负温范围内,AHFO 法测量所得冻土导热系数与土体初始温度之间仍然符合式( 4)所述线性关系。
值得注意的是,在初始温度T0=-0.6 ℃时,所测导热系数小于λ0,测量值为1.4 W/( m·K)-1。这可能是因为试验所使用土壤的近相变区位于-0.6 ℃附近,该温度条件下未冻水含量随温度急剧变化,大量热量转化为相变潜热而不是通过热量传导消散,导致测量误差较大。这说明,基于AHFO的导热系数测定方法不适用于近相变区( -0.6 ℃附近区间) 的冻土。
3.2 相变热容影响的误差分析
根据式( 5) 、式( 6) 可得冻土试样在不同初始温度下的体积热容Cv。将计算得到的体积热容Cv和导热系数λ 代入式( 10) ,可以获得不同初始温度下冻土试样的温度增量计算值ΔTc( r,t) 。图5 ~图7将其和实测温度分布ΔTs( r,t) 进行了对比。
由图5、图6 和图7 中实测、计算温度分布曲线都可以看出,在试验所使用加热功率和加热时间条件下,FBG 刚玉管传感器在冻土试样中的影响半径小于5 cm,说明试验所选用环刀尺寸可以有效避免边界效应所带来的测量误差。
图5a、图6a、和图7a 所示实测温度ΔTs( r,t) 普遍大于图5b、图6b 和图7b 所示计算温度ΔTc( r,t) ,这是由于测量过程中伴随着冰水相变,融化冰的比例随温度和温度的升高而增大。而冰的热容约为2000 J·( kg·K)-1,潜热为3.55×105iJ·( kg·K)-1,融化1 g 冰所需的热量可以使178 g 冰的温度升高18 ℃,换言之,冰的融化会减小冻土升温幅度。所以,即使在远低于名义冻结温度的情况下,忽略融化也会影响分析结果。
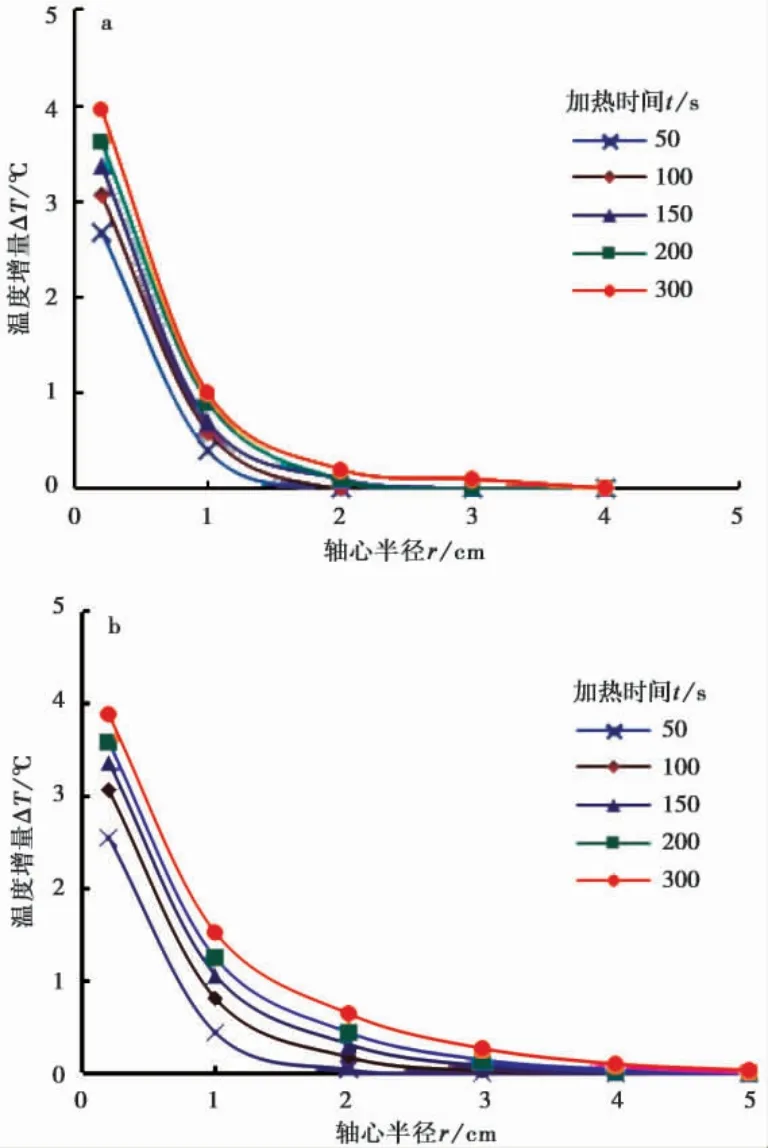
图5 初始温度-3.2 ℃下实测和计算温度分布曲线Fig. 5 Measured and calculated temperature distributions at the initial temperature of -3.2 ℃
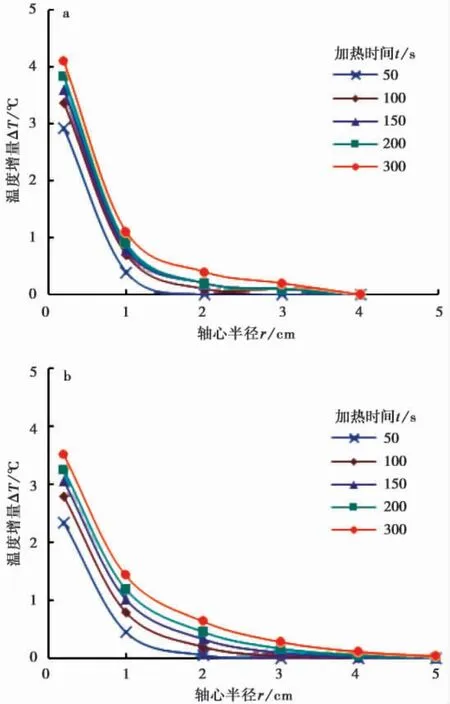
图6 初始温度-6.7 ℃下实测温度和计算温度分布曲线Fig. 6 Measured and calculated temperature distributions at the initial temperature of -6.7 ℃
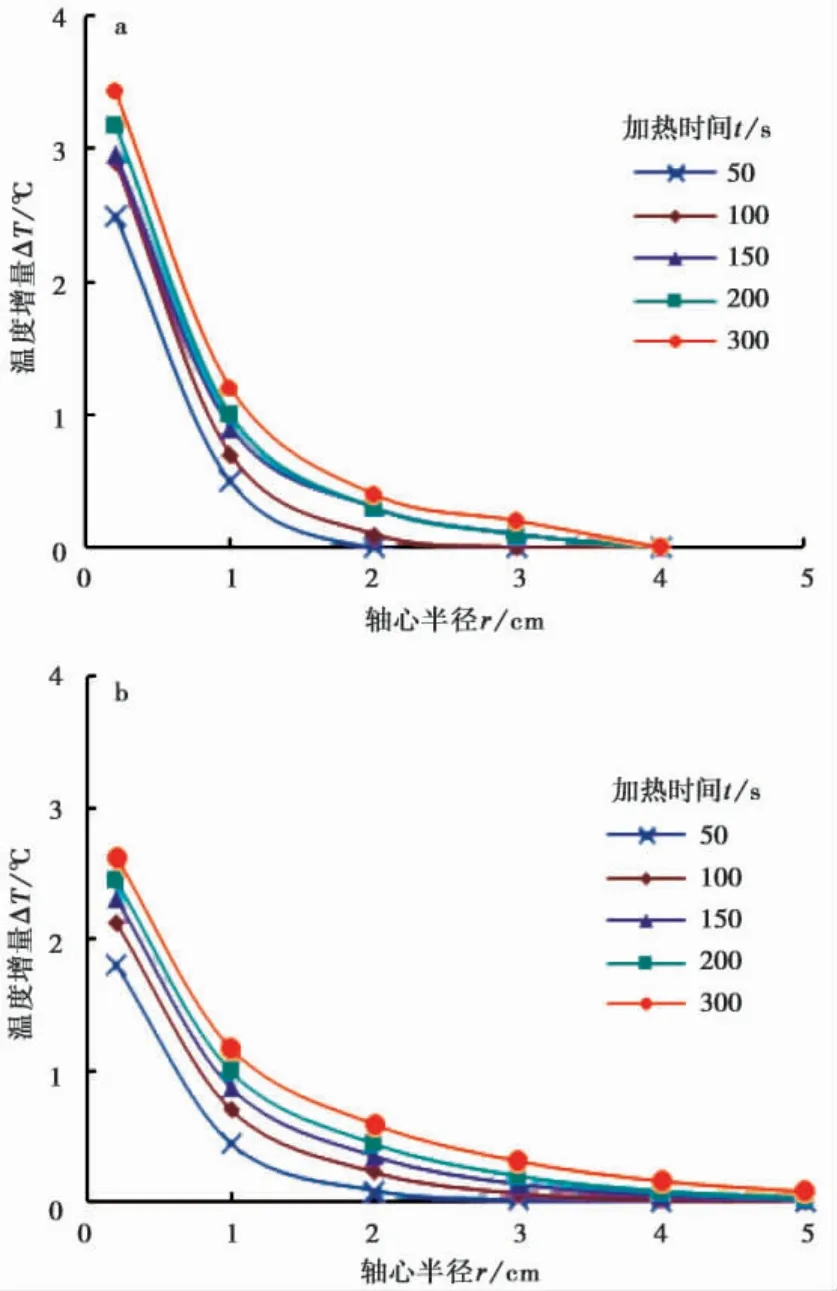
图7 初始温度20.6 ℃下实测温度和计算温度分布曲线Fig. 7 Measured and calculated temperature distributions at the initial temperature of 20.6 ℃
表1 为加热300 s 时冻土试样各半径实测温度和计算温度误差参数RMSE 与初始温度的关系。可以看出,在温度低于0 ℃时,RMSE 随温度升高而增大,在近相变区达到最大。表明相同的加热功率和加热时间,冻土试样的相变随初始温度升高而逐渐剧烈,由相变影响的实测温度和计算温度误差随之增大。
根据式( 8) 、式( 10) 和加热300 s 时、距离试样轴心2 cm 处的实测温度可反演不同初始温度下冻土试样的表观热容C,进而计算出相变热容CL。 图8 显示,随着初始温度升高,冻土体积热容变化较小; 在很低的负温下( 小于-6 ℃) ,相变热容趋于稳定; 在-6 ~0 ℃,相变热容随温度升高逐渐增大,且变化趋势愈渐强烈; 在温度高于-5 ℃时,相变热容甚至大于冻土自身的体积热容。此现象说明,在较低的负温下对冻土主动加热所引起的测量误差较小,在较高的负温下( 大于-5 ℃) 由于剧烈相变带来的误差随温度增高逐渐增大。这很好地解释了表1 中实测温度与计算温度误差参数随初始温度升高而增大的现象。

表1 温度分布误差分析Table 1 Error analysis of temperature distribution
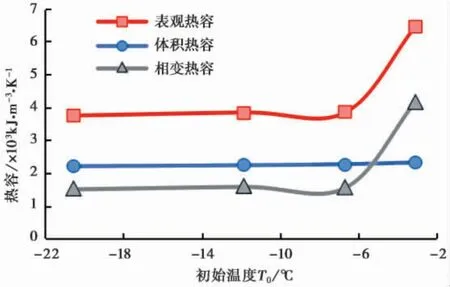
图8 热容随初始温度变化曲线Fig. 8 Relationship between heat capacity and initial temperature
4 结 论
本文基于主动加热法和线源模型,应用自主研发的FBG 刚玉管传感器对冻土温度场进行了监测;在考虑未冻水和相变潜热的情况下分析了冻土热响应特征,计算、反演出冻土导热系数和相变热容,分析验证了其与土体初始温度之间的关系,为冻土含冰量AHFO 测量法的修正提供了理论支撑。本文得到以下结论:
( 1) 在加热功率q =23 W·m-1,加热时间t=300 s 的情况下,试验结果显示,温度增量ΔT( t) 与时间对数lnt 之间具有良好的线性关系,说明线源模型测量冻土导热系数过程中,冻土导热系数变化较小,AHFO 法的适用性良好。
( 2) 随着冻土初始温度升高,冻土导热系数测量值与初始温度呈线性关系; 该线性关系为基于FBG 的含冰量测量方法的修正提供了参考依据和理论支撑。
( 3) 在温度低于-6 ℃时,相变热容趋于稳定;在-6~0 ℃时,相变热容随温度升高逐渐增大,且变化趋势愈渐强烈; 在温度高于-5 ℃时,相变热容甚至大于冻土自身的体积热容。
本文研究结果为冻土含冰量AHFO 测试方法的修正提供了实践意义上的可行性验证,进一步明确了传感器所测温度特征值与含冰量、总含水量之间的指数关系,与初始负温之间的倒数关系。但是本文结论是基于有限的室内试验得到的,这种关系是否适用于其他类型的冻土,以及如何通过标定确定参数间换算的经验系数,仍然是值得深入研究和探讨的问题。

