基于SARIMA模型的河北省葡萄价格预测分析
张兵 白思远 蒋冰执 曹薇 王俊芹

摘 要:利用2012年1月至2019年4月河北省葡萄市场价格数据,采用SARIMA模型对葡萄价格进行了短期预测分析。结果表明:葡萄市场价格具有较为明显的季节性特征,2019年葡萄价格的最高值比最低值高49.79%,波动幅度较大。葡萄种植户在今后的生产中,应注重提高葡萄品质,可通过开办直卖店、利用电商平台等新销售模式拓展销售渠道,以减缓葡萄市场价格波动,降低收入风险。
关键词:葡萄价格;SARIMA模型;预测
中图分类号 F323文献标识码 A文章编号 1007-7731(2019)17-0159-03
Prediction and Analysis of Grape Price in Hebei Province Based on SARIMA Model
Zhang Bing1 et al.
(1School of Economics and Trade,Hebei Agricultural University,Baoding 071000,China)
Abstract:Based on the grape market price data of Hebei Province from January 2012 to April 2019,this paper uses SARIMA model to make short-term forecast analysis of grape price. The results showed that the market price of grapes had obvious seasonal characteristics. In 2019,the highest price of grapes was 49.79% higher than the lowest price,and the fluctuation range was large. Grape growers should pay attention to improving the quality of grapes in production. In sales,new sales modes such as opening direct stores and using e-commerce platform can expand sales channels,slow down price fluctuation of grape market and reduce income risk.
Key words:Grape price;SARIMA model;Prediction
河北省是我國重要的葡萄产区,种植历史悠久。2017年,河北省葡萄种植面积42700hm2,产量1116000t,分别占全国种植面积、产量的8.5%、6.1%,面积和产量分别位居全国第3、4位。近年来,随着葡萄栽培模式的不断创新,形成了以张家口怀来和秦皇岛昌黎为主的露地栽培区以及衡水饶阳为核心的设施葡萄栽培区,错季栽培模式的发展,大大延长了葡萄的上市周期。但不同上市时间对葡萄价格的影响较大,掌握葡萄价格波动规律,对葡萄未来价格的走势进行预测,有利于果农进行科学决策,提高收入,促进果农与现代农业发展的有效衔接。
针对农产品价格波动的分析及预测,国内学者已开展了较为深入的研究,提出了不同的价格波动分析和预测模型。李干琼等(2011)分析了季节虚拟变量法、Census X12法、移动平均比率法、Holt-Winters季节指数平滑法、SARIMA法等短期预测模型的预测效果,提出单一模型预测误差波动较大,总体上预测准确度随着预测周期变长而下降;王川等(2013)以双指数平滑模型、Holt-Winters乘法模型、ARIMA(1,1,4)模型为基础建立组合模型,对我国苹果市场价格进行了短期预测;罗长青等(2013)采用SARIMA模型对平菇价格进行了预测分析;王宝海等(2016)通过构建ARIMA(1,1,1)模型对我国大宗农产品价格指数进行了预测;徐雅卿等(2017)用指数平滑模型以及ARIMA模型,对西安朱雀市场胡萝卜价格进行了短期预测;王美凤等(2017)用SARIMA模型对上海青菜的平均价格进行了预测。
综合以上分析,用于预测的定量分析方法较多,但是适用范围不同。SARIMA方法是预测农产品短期价格波动精确度较高的定量分析方法,能够考虑到农产品价格受季节性、随机趋势、周期性等多种因素的影响。但不同的农产品价格波动规律存在较大的差异性,运用SARIMA模型分析葡萄价格波动规律的研究较少。为此,本研究基于SARIMA模型,利用2012年1月至2019年4月河北省葡萄月度价格数据,探索葡萄价格波动的内在规律,对葡萄未来价格走势进行短期预测。
1 研究方法
SARIMA模型(Seasonal Auto-regressive Integated Moving Average)又称乘积季节自回归移动平均模型。是以Box、Jenkins创立的随机时间序列ARMA模型为基础改进形成。SARIMA模型的基本思想是:首先对时间序列进行平稳性检验,其次对存在趋势性与季节性的非平稳序列,经过几次逐期差分和季节差分消除序列规律性。平稳时间序列[Xt]的ARMA(p,q)模型的形式为:
[Xt=] [φ1Xt-1+φ1Xt-2+…φpXt-p+ut-θ1ut-1ut-]
[θ2ut-2-…-θqut-q]
其中,[φ1],[φ2],…,[φp]与[θ1],[θ2],…[θq]分别表示自回归参数和移动平均参数。p表示自回归部分的滞后阶数,q表示移动平均部分的滞后阶数。随机项[ut]是相互独立的白噪声序列。引入滞后算子[Bk],则有[BkXt=Xt-k],所以ARMA(p,q)的基本形式为[φ(B)Xt=θ(B)ut]。
在时间序列[Xt]非平稳,且经过d阶差分后平稳的条件下,序列[Xt]表示为ARIMA(p,d,q)模型,形式为[φ(B)?dXt=θ(B)ut],其中,d阶的逐期差分为[?d=(1-B)d]。而在序列[Xt]非平稳,且d阶差分后,还需要经过D阶季节性差分的条件下,序列[Xt]需建立[ARIMA(p,d,q)(P,D,Q)S]模型,其形式为
[φ(B)?(B)S?d?DSXt=θ(B)Θ(B)Sut]
即SARIMA季节模型,其中,D阶的季节性差分表示为[?DS=(1-BS)D],s为季节周期,[?(B)S]为季节自回归算子,[Θ(B)S]为季节移动平均算子。
2 模型构建与实证分析
2.1 数据来源及变量说明 本文数据来源于农产品价格信息网,采用2012年1月至2019年4月的月度数据,有效数据是88个。
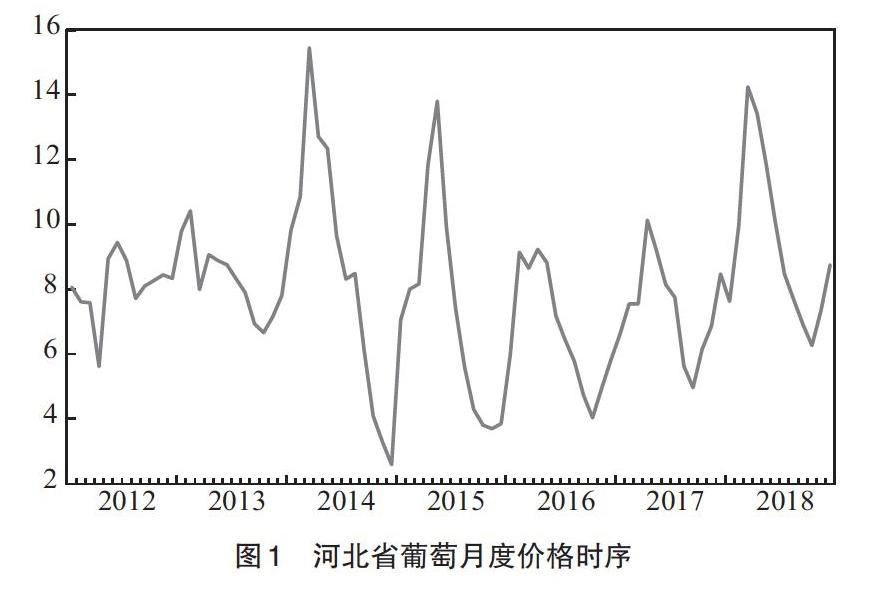
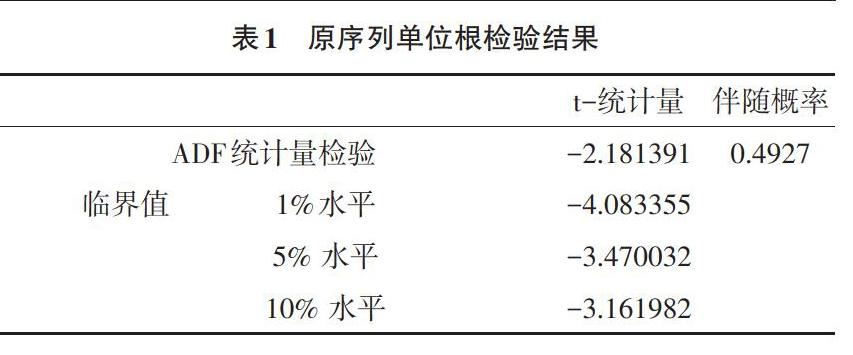
2.2 模型平稳性检验 将2012年1月至2019年4月的月度价格数据用时间序列[Xt]表示,用统计软件Eviews8.0,绘制样本数据的时间序列图(图1),初步判断原序列非平稳。进一步对葡萄月度价格数据序列进行ADF单位根检验,判断序列的稳定性。结果显示(表1),在3种不同显著性水平下,不拒绝原假设,所以原序列非平稳。
2.3 季节性检验 对时间序列[Xt]进行平稳化处理,首先对序列进行一阶差分。通过差分后序列的自相关-偏相关图可以判断序列自带周期为12的季节波动,为更好的对样本数据进行拟合,需进一步消除季節性,做季节性差分(图2)。对经过一阶差分和季节差分处理后的序列进行单位根检验,考虑仅存在高阶滞后项的检验方程,结果显示t统计量为-9.9924,小于显著水平[a=0.01]的临界值-4.0946,拒绝原假设,序列满足Box-Jenkins模型平稳的建模要求。
2.4 葡萄价格波动规律模型构建 利用Box-Jenkins方法建模,首先需要对模型进行识别,特别是滞后阶数的选择,然后对模型进行检验、参数估计及预测。根据样本序列经过一阶差分和季节差分后平稳,考虑建立SARIMA(p,d,q)(P,D,Q)s模型进行分析预测。利用序列的自相关和偏相关图进行综合分析,预选模型初步为SARIMA(1,1,1)(1,1,1)12、SARIMA(1,1,2)(1,1,1)12、SARIMA(2,1,1)(1,1,1)12和SARIMA(2,1,2)(1,1,1)12。利用2012年月至2018年12月的葡萄价格数据,通过对预选模型的拟合优度进行比较(表2)。从表2可以看出,模型SARIMA(1,1,1)(1,1,1)12的[R2]最大,AIC、SC、H-Q系数最小,可初步将其确定为葡萄价格的预测模型。
进一步对SARIMA(1,1,1)(1,1,1)12模型的残差序列进行Q统计量的检验,检验结果p值均大于显著水平0.05,表明残差序列为白噪声序列,则模型建立合理。模型的具体形式为:
[(1+0.7326B)(1-0.6719B12)(1-B)(1-B12)=]
[(1-0.9866B)(1+0.9168B12)]
2.5 预测分析 模型的预测效果通常用平均绝对百分误差(Mean absolute percentage error,MAPE)和根均方百分误差(Root mean square percentage error,RMSPE)2个统计量反映。其中,MAPE计算方法相对简单,实用范围较广。其计算公式为:
[MAPE=-1ni=11pi]
式中,n为样本数据个数,[pi]为相对误差百分比。
运用SARIMA(1,1,1)(1,1,1)12模型进行预测,2019年1—12月份葡萄价格的预测值为8.37元/kg、10.81元/kg、14.04元/kg、13.85元/kg、12.11元/kg、10.51元/kg、9.16元/kg、8.35元/kg、7.54元/kg、7.05元/kg、8.19元/kg、9.71元/kg,实际值与预测值的拟合效果如图3所示。1—4月份的预测值与实际值9.65、10.48、11.04、13.75的误差率为13.26%、3.15%、27.17%、0.73%,平均误差率为11.07%,模型的平均绝对百分误差MAPE=12.2。根据Delurgio(1998)区分,依照MARE和RMSPE的大小可知,模型预测效果良好。
3 结论及建议
(1)葡萄市场价格波动的季节性特征较为明显,2—5月葡萄价格处于全年领先水平,6月后价格有所下降,10月后开始回升;葡萄全年价格落差较大,最高价和最低价相差12.87元/kg。从2019年葡萄市场价格预测值看,走势依旧遵循以往的规律,全年最高价比最低价高49.79%,波动幅度较大。葡萄种植户今后应准确把握葡萄市场价格的变动规律,在生产中着重提高产品品质,在现代消费者追求食品质量安全的前提下,实现葡萄生产的绿色、高质、可持续发展。在产品进入上市期时,可通过开办直卖店、利用电商平台等新销售模式拓展销售渠道,减缓葡萄市场价格波动,降低收入风险。
(2)本文以河北省2012—2019年月度市场价格建立时间序列模型,并对其变化趋势进行分析发现:葡萄价格有上升趋势但不明显,反映出目前河北省葡萄市场处于近饱和或已经饱和状态。因此,今后应该着眼于市场的需求变化,着重提升葡萄产品质量,优化品种结构,加强对省外及国际市场的输出,提高效益。
参考文献
[1]李干琼,许世卫,李哲敏,等.农产品市场价格短期预测方法与模型研究——基于时间序列模型的预测[J].中国农业大学学报,2011,16(02):172-178.
[2]王川,赵俊晔,赵友森.组合预测模型在农产品价格短期预测中的应用——以苹果为例的实证分析[J].系统科学与数学,2013,33(01):89-96.
[3]罗长寿,周丽英.季节时间序列模型在平菇价格预测中的应用[J].贵州农业科学,2013,41(11):202-204,209.
[4]王宝海,丁慧媛.基于ARIMA模型的我国大宗农产品价格指数预测[J].数学的实践与认识,2016,46(21):37-43.
[5]徐雅卿,魏轶华,李旭刚.农产品价格预测模型的构建[J].统计与决策,2017(12):75-77.
[6]王美凤,赵京音,邵芳,等.上海青菜价格短期预测模型的比较研究[J].上海农业学报,2017,33(01):160-165.
[7]张丽,牛惠芳.基于SARIMA模型的居民消费价格指数预测分析[J].数理统计与管理,2013,32(01):1-6.
[8]张瑛,朱玉贵.水产品价格预测与我国渔业经济可持续发展——以山东省水产品价格为研究样本[J].厦门大学学报(哲学社会科学版),2017(06):57-64.
[9]De Lurgio,SA,1998,Forecasting principles and applications.RICHARD D.IRWIN,INC.
(责编:张宏民)

