基于RS-改进云模型的岩爆倾向性预测
黄明健,王加闯,过 江
(1.湖南涟邵建工(集团)有限责任公司,长沙 410011;2.中南大学 资源与安全工程学院,长沙 410083)
岩爆又称冲击地压,是指地下硐室在开挖过程中,处在高地应力状态的硬脆性岩体,由于硐体周围应力集中而引起弹性应变能突然、快速的释放,在其极限平衡状态下受到破坏时,向自由空间突然释放能量的动力失稳现象[1-2],是一种采矿或隧道开挖活动诱发的地震。岩爆灾害具有突发性、难控制性和破坏范围大等特点,通常会伴随着围岩的剥离、岩体剥落和弹射、较大的粉尘和空气冲击波,很容易造成群死群伤事故[3]。我国岩土工程建设规模大、难度高,因此岩爆灾害发生的频率和强度也呈不断上升的趋势。如何在地下工程和岩土工程实践中正确的对岩爆等级进行预测成为必须解决的问题。
针对岩爆问题的不确定性,国内外学者对岩爆倾向性预测做了大量的研究工作,并提出了多种岩爆分级预测方法,如理想点法[4]、模糊综合评价方法[5]、神经网络法[6]、距离判别法[7]、等效数值法[8]、云模型法[9]、遗传算法[10-11]、可拓模型[12]等。这些理论和模型在一定程度上完善了岩爆预测分级评价体系,但是部分方法无法克服自身缺陷,特别是由于实际工况和岩爆发生原因的复杂性,这些理论和实际的生产仍有部分偏差:主成分分析法在进行替代过程时,可能会造成部分指标反映的信息被忽略,对原始问题的评价缺乏全面性;熵值法计算前提是指标间不存在相关性,否则会对评价对象进行重复评价,使得计算结果有失偏差;可拓模型仍采用了主观赋值权重的方法,在计算中可能会忽略一些重要的约束条件;神经网络算法获取的样本代表性不强,而且拟合速度难以控制,很容易造成偏差;传统的正态云模型可能会忽略指标之间的相关性,而且指标的分布并不是完全服从正态分布。
鉴于以上算法存在的部分缺陷,本文提出了基于粗糙集理论和改进的正态云模型,即部分区间服从正态分布的有限区域云模型[7]。由于岩爆预测存在着模糊性和随机性,利用传统的正态云模型在处理单区间边界的参数分布时,不会考虑实际情况和模型分布的偏差,这种情况求取的计算结果往往与实际工程存在差异,影响预测结果的准确性。在对岩爆等级进行分类评价时,指标权重的确定是对象评价的关键,传统的客观求取权重的方法虽然以客观数据为基础,但是结果解释性较差,为此本文选取基于粗糙集理论的权重确定方法[13],这种方法不需要任何的先进经验,即可完成权重的计算,再结合改进的云模型,可以使岩爆分级结果更为准确、客观,为岩爆预测方法提供新思路。
1 理论基础
1.1 云模型理论
云模型理论是由李德毅等[14]提出的一种处理模糊问题的抽象模型,它是从隶属度的角度出发处理数据的模糊性和随机性,通过将定性描述与定量数据进行分析转换,进而获得想要的结果。该方法已经应用在实际生产的多个领域,并取得了良好的效果。
1)云的基本概念
存在一个精确数值表示的定量集合U={x},U为论域(1维、2维或多维),小区间Ak是论域U中的模糊集合,K为论域分割的等级区间数,C是Ak上的定性概念,Ak中存在任意元素x,且每对应一个x∈Ak,都有一个稳定倾向的随机数作为映射μ:x→μA(x),在定性概念C上随机实现,μA(x)叫做x对概念C的确定度,也可称为隶属度,μA(x)在论域U上的分布称为云模型,μA(x)∈(0,1),即:
(1)

2)数字特征
通常云模型概念的支撑,主要利用三个数字特征值来加以表述[14],即期望Ex、熵En、超熵He。期望Ex表征数据参数在论域空间的中心值,从几何意义上讲,表示图像最高点对应的随机数值,决定了云滴分布的位置;熵En表示在论域区间被定性概念表述的云滴的取值范围,反映了基本概念的模糊性和随机性,该值也决定了云滴的混乱程度,云图某一量度宽度越大,代表云滴的取值范围越大,那么其定性概念就越模糊,云滴的离散程度越大,反之亦然;超熵He,也就是熵的熵,表示熵的不确定性,在云图中,通常可以确定云的厚度,超熵越大,云越厚。
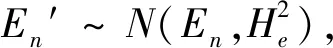
(2)
边界值Ck,是两个级别的过渡值,同时隶属于两个模糊区间的隶属度是相等的[15],即:
(3)
(4)
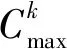
(5)
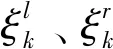
(6)
同理也可求出指标值越大,等级区间越小型指标属于等级k的左、右半区间长度:
(7)
3)云发生器
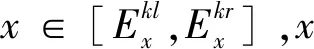
(8)
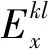
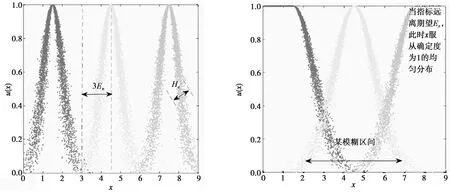
图1 传统云模型与改进云模型Fig.1 Traditional cloud model and finite-interval cloud model
1.2 粗糙集理论
1)决策表
粗糙集理论是利用一个四元组S=(U,A,V,f)来描述一个知识系统[16]:S表示一个信息表达系统,也可称为信息系统;U代表所要研究对象的非空集合,即研究对象论域U={xi},xi表示论域中的单个研究对象;A表示研究对象的属性集合,包括用来描述xi主要特征的条件属性C(c1,c2,...,cn)和决策属性D(d1,d2,...,dm),A=C∪D,C∩D=Φ;V表示属性集合A对应的属性值;f表征一个信息函数,可以对每个对象进行属性赋值,对于U中的任意元素x,都有f:A(C,D)→V(c,d)。通过该系统及其属性进而将评价对象和评价指标进行关联,利用信息函数转化的属性值来对评价对象进行描述,再利用粗糙集运算,进而求出各指标权重完成对评价系统的评价。信息系统S称为决策表。
2)不可辨识关系和上下近似
根据粗糙集理论知识,一个知识库表征的是一个关系系统,记作序偶K=(U,R),K称作一个近似空间,关系R是论域U上的一个等价关系,称为K上的难辨别关系[17],简称难辨关系,记为:
IND(R)={(x,y)∈U×U|∀a∈A,
f(x,a)=f(y,a)}
(9)
U/IND(R)称为U的划分,其中任意的元素称为等价类。
粗糙集理论通常会利用上近似集合和下近似集合进行描述一个粗糙集。对于一个给定的知识表达系统,可得以下定义:若X是论域U的任意非空子集,X⊆U存在一个不可辨认关系IND(R),则集合X的R上下近似集合可分别表示为(下近似集合也称作正域):
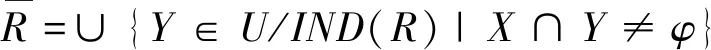

(10)
3)知识依赖度与属性重要度
表征岩爆等级程度的评价指标,也称作条件属性,在岩爆等级分析中,对于某个评价对象属性的表示,可以利用正域加以衡量。属性知识在多大程度上依赖其正域,通常利用知识依赖度表示:设K=(U,R)表示一个知识库,其中P和Q都是R的子集,则Q对P的依赖度可表示为[16]:
(11)
式中:posp(Q)表示Q在P下的正域,|U|和|posp(Q)|表示所含元素的个数。当γp(Q)=1时,称Q完全依赖于P;当γp(Q)=0时,称Q完全独立于P;当γp(Q)介于0~1时,称Q粗糙依赖于P。
在决策表中,若U/C={x1,x2,...,xn},U/D= (Y1,Y2,...,Yn},若对任意ci⊆C,则ci对决策属性D的重要性为:
σCD(ci)=γc(D)-γC-ci(D)
(12)
2 RS—改进云模型的岩爆预测及计算流程
利用RS—改进云模型进行岩爆预测,要选取适当的评价指标体系及其相对应的评价标准,通过粗糙集理论进行指标权重的计算;再利用相应的评价指标标准,计算各等级云特征参数,利用云发生器生成云模型图;根据样本实测数据计算各指标对应的各级别确定度;最后计算综合权重值,按照最大隶属度原则确定岩爆危险性等级。评价流程图如图2所示。

图2 岩爆倾向性评价流程图Fig.2 Rockburst tendency evaluation flow chart
2.1 评价指标的选取及分类标准的确定
影响岩爆等级的因素众多,评价指标的选取会反映整个评价过程是否合理,指标过多会使评价过程复杂,且有些实测数据不易获取,评价指标过少则会使得评价结果不严谨。从影响岩爆产生的内部因素和外部因素综合考虑,围岩应力、岩性和能量是影响岩爆等级的主要因素,参考相关文献,本文选取岩石单轴抗压强度σc、岩石抗拉强度σt、切向应力σθ、弹性变形能Wet作为主要评价因子[18-20]。
参照相关研究及分类标准,可以将岩爆烈度分为四个等级[7]:一级(无岩爆),主要表现为岩壁没有出现撕裂、碎石崩落等现象,无声发射现象,不需要采取任何安全措施;二级(微弱岩爆):岩壁表面松脱、剥落掉块,需要采取安全措施并要进行安全监管措施;三级(中等岩爆):硐室、巷道壁岩石出现块状剥落并伴有偶尔的抛射现象,时常发出尖锐的弹射声,可能引起人员伤亡和财产损失,要采取实施监控措施,做好隔离防护工作;四级(剧烈岩爆):大块岩体剥落、围岩急剧变形,爆坑大量出现,极易发生群死群伤事故,必须采取相关的安全防护措施。具体分类标准如表1所示。
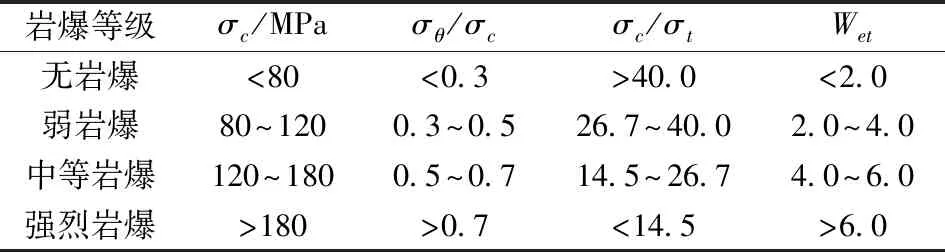
表1 岩爆倾向性等级划分Table 1 Rockburst tendency classification
基于表格中的评价标准,参照公式(4)-(7),可计算云特征参数Ex、He、En,根据求得的云模型特征参数值,利用MATLAB模拟器,通过正向云发生器生成各评价指标云滴图,具体生成图如图3所示。

图3 云滴图的生成Fig.3 Generation of the cloud droplet graph
2.2 岩爆倾向性粗糙集定权思路
在评价过程中,最重要的是确定评价因子的权重。所谓权重,是指在评价过程中影响问题的因素的重要程度,这种重要度可通过定性描述,也可依据具体数据进行定量计算。根据粗糙集理论,通过构造一个知识系统,将影响岩爆危险性的评价指标的权重问题转为属性重要度计算问题。具体定权步骤如下[16]:
STEP 1:将评价对象的原始数据经离散化处理,生成二维决策表。将影响岩爆的评价指标视为决策表中的条件属性C={c1,c2,...,cn},危险性分级视为决策属性D={d1,d2,...,dm}。
STEP 2:计算属性依赖度。利用式(11),计算决策属性D对条件属性C的依赖度:
(13)
在剔除某一属性ci后,决策属D对条件属性集c-ci的依赖度为:
(14)
STEP 3:计算单个评价因子重要度:
σCD(ci)=γc(D)-γc-ci(D)
(15)
STEP 4:归一化处理。通过归一化运算,计算出不同条件属性的权重系数,即不同评价指标的权重:
(16)
2.3 综合权重的确定
经过上述步骤的计算与分析,我们可以得出不同的条件属性(评价指标)实测值x隶属于不同模糊区间Ak的确定度μ(x),结合粗糙集理论的定权方法,进而求出最终的综合确定度公式:
(17)
式中:μk,i—待测样本的第i个指标的实测值所在等级k的确定度;ω(Ei)—待测样本第i个评价指标所占权重的大小。
根据最终的确定度,按照最大隶属度原则,确定样本岩爆的隶属等级:
L=max(μ1,μ2,...,μk)
(18)
3 岩爆预测应用
为考察该模型优良性,本文从文献[21]中选取40组国内外岩爆实测数据作为训练样本进行有效性检验。U{x1,x2,...,x40}表示研究对象的论域;A=C{c1,c2,c3,c4}∪D{d}表示决策对象的属性集合,其中:c1(σc)、c2(σθ/σc)、c3(σc/σt)、c4(Wet)为条件属性,为计算方便,根据不同影响因素的分类标准,取聚类数为4,各因素因实际测量值不同分别取{1,2,3,4}对应实际值由低到高变化;D(d1,d2,d3,d4)为决策属性,{1,2,3,4}分别对应实际岩爆等级Ⅰ(无岩爆),Ⅱ(微弱岩爆),Ⅲ(中等岩爆),Ⅳ(剧烈岩爆)。具体的实测值、原始决策表如表2所示。
表2 原始决策表Table 2 Original decision table

实例序号条件属性σcσθ/σcσc/σtWet岩爆等级UAC1C2C3C4D1180.00 0.27 21.69 5.00 Ⅲ1313332175.00 0.36 24.14 5.00 Ⅲ2323333180.00 0.42 21.69 5.00 Ⅲ3323334180.00 0.32 21.69 5.00 Ⅲ4323335236.00 0.38 28.43 5.00 Ⅲ5422336130.00 0.38 21.67 5.00 Ⅲ6323337140.00 0.77 17.50 5.50 Ⅳ7343348178.00 0.11 31.23 7.40 Ⅰ8312419115.00 0.10 23.00 5.70 Ⅰ92133110176.00 0.31 24.11 9.30 Ⅲ103234311120.00 0.40 80.00 5.80 Ⅲ112213312115.00 0.55 76.67 5.70 Ⅲ122313313110.00 0.45 73.33 5.70 Ⅲ13221331482.56 0.37 12.70 3.20 Ⅱ142242215128.60 0.69 9.74 4.90 Ⅳ153343416237.10 0.05 13.43 6.90 Ⅰ164144117256.50 0.22 13.57 9.10 Ⅲ174144318225.60 0.40 13.12 7.30 Ⅳ184244419171.50 0.36 7.59 7.50 Ⅱ19324422054.20 0.63 4.48 3.17 Ⅱ201342221138.40 0.78 17.97 1.90 Ⅳ213431422198.00 0.35 8.84 4.68 Ⅱ224243223171.30 0.61 7.58 7.27 Ⅳ233344424237.16 0.44 13.43 6.38 Ⅳ244244425304.21 0.35 14.56 10.57 Ⅳ25423442654.20 0.47 21.77 3.17 Ⅱ261232227147.09 0.49 13.40 6.53 Ⅲ273244328160.00 0.14 30.77 2.22 Ⅰ283122129160.00 0.13 30.77 2.22 Ⅰ293122130160.00 0.08 30.77 2.22 Ⅰ303122131170.00 0.44 15.04 9.00 Ⅲ313234332123.00 0.35 20.50 5.00 Ⅲ323233333165.00 0.38 17.55 9.00 Ⅲ33323433488.70 0.34 23.97 6.60 Ⅲ342234335128.61 0.82 9.89 5.76 Ⅳ353443436304.00 0.35 33.33 5.76 Ⅲ364223337306.58 0.34 22.06 6.38 Ⅳ37423443852.00 0.14 14.05 1.30 Ⅰ38114113999.70 0.25 20.77 3.80 Ⅰ39213214099.70 0.15 20.77 3.80 Ⅰ4021321
根据前文粗糙集理论知识,对表中数据按照条件属性和决策属性进行划分,则有:
U/IND(C)={x1,x2,x3,...,x40}
U/IND(D)={{x8,x9,x16,x28,x29,x30,x38,x39,x40},{x14,x19,x20,x22,x26},{x1,x2,x3,x4,x5,x6,x10,x11,x12,x13,x17,x27,x31,x32,x33,x34,x36},{x7,x15,x18,x21,x23,x24,x25,x35,x37}}
依次去掉一个条件属性后,对论域等价划分得(由于篇幅有限,本文仅以条件属性c1为例,简述计算方法):
U/IND(c-c1)={{x1,x9},{x2,x3,x4,x6,x32},{x5,x36},{x7},{x8},{x10,x25,x31,x33,x34,x37},{x11,x13},{x12},{x14},{x15},{x16,x17},{x18,x19,x24,x27},{x20},{x21},{x22},{x23},{x26},{x28,x29,x30},{x32},{x35},{x38},{x39,x40}
计算在条件属性c1下,决策属性D的正域为:
POCC-C1(D)={x2,x3,x4,x5,x6,x7,x8,x11,x12,x13,x14,x15,x20,x21,x22,x23,x26,x28,x29,x30,x32,x35,x36,x38,x39,x40}
计算在剔除决策属性c1,决策属性对条件属性C-C1的依赖度为:
计算条件属性c1对决策属性的重要度为:
同理,按照上述步骤计算,可得出条件属性C对决策属性D的重要度分别为0.273、0261、0.227、0.239。根据权重计算,再结合云模型求解的不同指标隶属于不同岩爆等级的重要度,根据式(17)即可算出不同实例样本的岩爆等级判定结果。
本文以样本1为代表数据,简述RS—改进云模型的岩爆等级预测方法。样本1的条件属性c2切向应力与单轴抗压强度比的实测值为0.27,根据云模型的基本概念以及公式,可计算出隶属于四种岩爆程度的确定度分别为:μ1=0.63,μ2=0.31,μ3=μ4=0。单从c2基本数值来看,该样本隶属于第一等级,但是由于c2评价因素所占权重不是很大,所以样本最终的隶属岩爆等级与通过这一条件属性计算有所偏差,经过最终的综合隶属度计算,该样本隶属于第三等级中等岩爆,与实际岩爆等级相符,因此分析时,绝不能拘于某一评级因子的隶属度。按照上述步骤进行计算,可计算出40组样本数据隶属于各岩爆等级的隶属度,并根据最大隶属度原则确定最终岩爆等级。实测样本隶属各等级的隶属度及最终评判结果如表3所示(注:*为误判)。
经与实际岩爆等级和其他方法[22]对比,本文所介绍的RS—改进云模型岩爆预测模型的预测结果与实际岩爆等级基本一致,且评判结果更加保守,具有一定的准确性。但是,由于岩爆问题具有一定的模糊性和不确定性,所以不能仅仅依据几个物理量来对实际的岩爆等级进行判定,还需要参考研究目标的地质地貌、内外环境和具体施工情况进行分析。例如样本序号27,根据本文构建模型和最大隶属度原则,该样本隶属于Ⅲ等级的可能性最大,隶属于Ⅳ等级的可能性和隶属于Ⅱ等级的数值相近,但是绝不可能隶属于第Ⅰ、Ⅱ等级,而此样本的实际岩爆等级为Ⅲ级中等岩爆,可以得出这样的结论:即使实际爆破等级为中等岩爆,但是不排除转向强烈岩爆这种情况的发生,所以预测结果具有一定的预见性和保守性。
4 工程实例
为检验本模型有效性和可行性,本文依托铜陵冬瓜山铜矿岩爆实测数据为待测样本。冬瓜山铜矿是铜陵有色金属集团控股有限公司的主要矿山,矿床为层控式矽卡岩型深埋矿床,埋深大于700 m,因此矿区原岩应力和矿岩强度比较高,所以在矿山开采过程中,岩爆的预测和预防已经是一项重大课题,而岩爆预测和防治必须建立在矿岩岩爆倾向性研究的基础之上。
在高应力作用下,冬瓜山矿在基建和生产期间在井巷施工中曾多次发生以岩石弹射为主要特征的岩爆破坏事件,为此岩爆倾向性预测也成为矿山防震减灾的一项重要技术手段。本文以冬瓜山-480 m~-730 m主矿体矽卡岩的物理力学性质为依据,具体评价指标如表4所示。
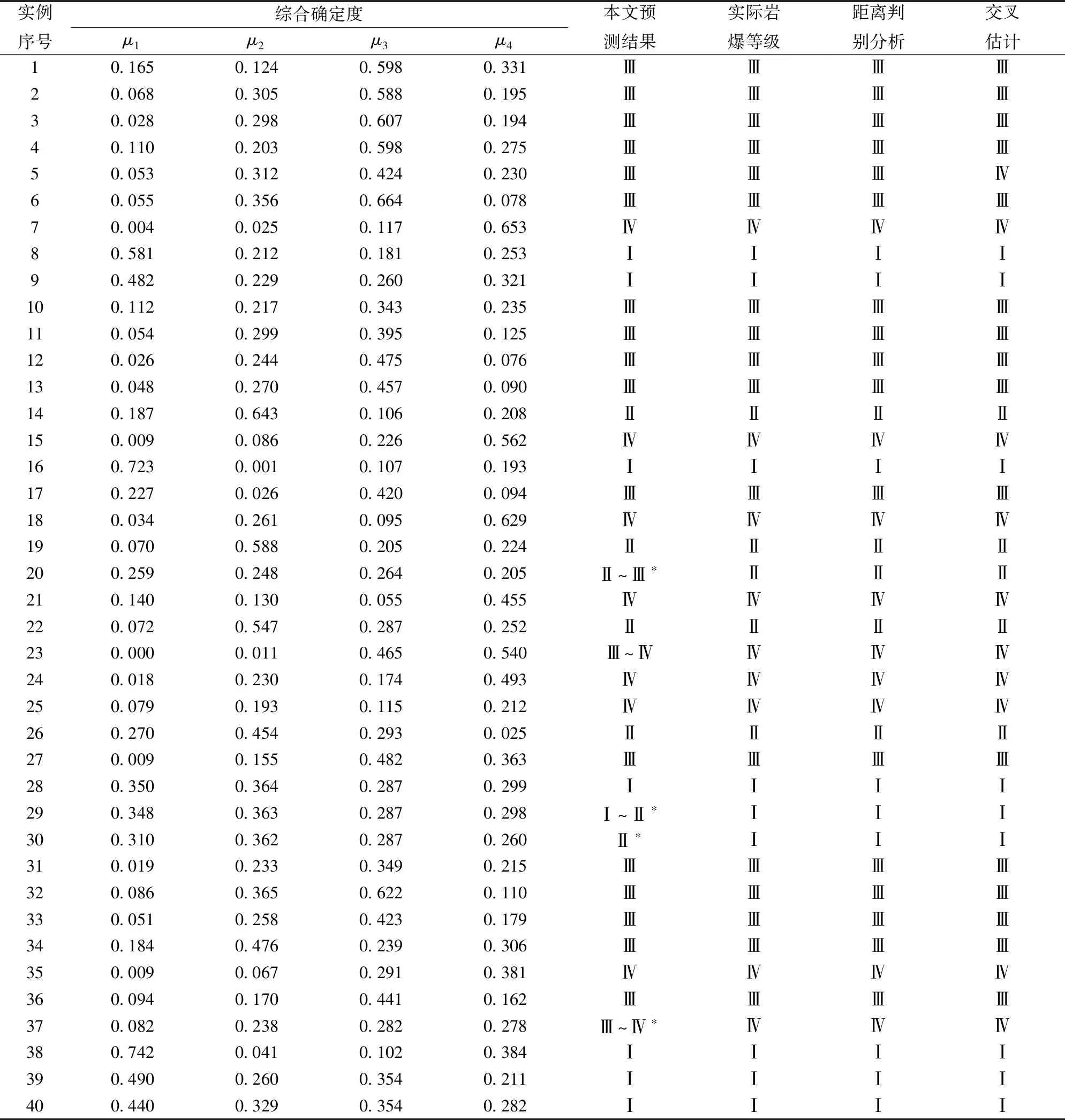
表3 实际样本隶属各级岩爆等级的综合确定度Table 3 The actual sample is subject to the comprehensive determination of the rockburst level of each level

表4 冬瓜山岩爆实测数据Table 4 Rockburst measured data of Dongguashan mine
根据前文所述方法,首先将指标分类的判别标准临界值代入公式(4)~(7)求出云模型的数字特征,根据正向云发生器,将指标实测值带入公式(2),求出不同指标下实测值对应的危险程度的隶属度μ(x);根据粗糙集理论,将实测值生成具体的原始决策表,参照公式(13)~(16),求取各评价因子的权重,再根据公式(17)求出样本的最终隶属度,确定实际工程的岩爆等级。经计算,依据粗糙集理论结合改进的云模型求出的冬瓜山岩爆等级与实际情况相符,说明该模型可行,为岩爆预测提供了新的途径。
5 结论
1)根据岩爆问题的模糊性和复杂性,通过对云模型的基本概念加入模糊区间的定义,使得传统云模型在定义上更加直观;将云模型特征参数求取方式上加以改进,使得求取结果与实际情况更加符合,强化了计算结果的准确性。
2)选取岩石单轴抗压强度σc、岩石抗拉强度σt、切向应力σθ、弹性变形能Wet作为主要评价因子,以国内外40组数据为学习样本,通过冬瓜山铜矿岩爆实测数据为待测样本验证其准确性。经计算,通过该模型确定的岩爆等级与实际岩爆等级大致相符,具有较好的预测性和科学性,为岩爆倾向性预测问题提供了新的思路。
3)粗糙集理论在求解权重问题时,可以通过对条件属性进行约简,求出条件属性对决策属性的重要度,进而使求取的权重更加客观、具体,减少评价过程的片面性。
4)利用粗糙集理论求取权重,所选取的数据应该具有代表性和客观性,避免评价结果的片面性;同时在对数据离散化处理之前,还可以利用多种方法对数据进行预处理,从而取其均值作为最终的指标权重,使评价结果更具有科学性。

