考虑同时取送随机需求的多行程车辆路径研究

(福州大学 经济与管理学院，福建 福州 350108)

引言

多行程车辆路径问题（Multi-Trip Vehicle Routing Problem，MTVRP）最早由Fleischmann提出[1]，在车辆从配送中心出发之后，允许车辆中途返回配送中心补货后再出发继续服务后续点，在配送中心和路径客户点之间进行多次往返完成配送任务，其具有能有效减少车辆使用数量、降低发车成本等优点，近年来受到学者们关注。

在多行程物流中，目前MTVRP研究集中于确定性多行程车辆路径问题，内容主要针对分配路线数量和限制车辆服务时间等方面。Francois等学者采用组合装箱构造初始路径集合后单独分配给车辆，并提出了大规模邻域搜索算法求解[2]；宋强等学者在约束条件下制定一组可行路线分配给车辆进行配送，提出改进的混合遗传算法求解带时间窗和发货时间的MTVRP[3]；Hernandez等开放车辆在途服务时间限制研究带时间窗的 MTVRP，并设计分支定价算法进行求解[4]；为研究允许车辆在工作日期间执行多趟配送任务的MTVRP，宋强等学者提出了改进迭代局部搜索算法、变邻域搜索算法进行求解[5-6]。

在实际物流活动中由于诸多因素存在，很多客户信息会表现出不确定性、变化性，研究主要集中于考虑客户的单向送货需求的不确定性、带不确定环境求解方法和动态调整策略等方面。王连锋等学者针对客户的模糊送货需求，分析了实际配送途中服务失败事件的可能性并建立模糊期望值模型，并设计了带双层禁忌的并行粒子群算法求解[7]；学者李阳和范厚明分别针对客户随机需求和模糊需求构建不确定问题模型，提出点返回多行程策略，并采用变邻域搜索算法进行求解[8-9]；Wassan等学者以最小化总成本为目标研究带回程取货的MTVRP，提出了两阶段邻域搜索算法[10]；张晓楠等针对带模糊送货需求的MTVRP，基于可信性测度理论构建预优化模型，提出了“基于调整成本期望值”的实时调整策略，并设计种群进化算法进行求解[11-12]。

综上所述，目前MTVRP的研究中，主要集中于确定性问题、不确定的单向送货需求及其求解算法的研究，考虑同时取送货、不确定需求的运输情况较少。而在MTVRP中，由于其可在运输途中多次往返，如何同时兼顾客户取送双向动态突发性需求，避免单向物流造成的车辆能力浪费，又能满足顾客个性化的需求，降低成本和提高配送效率，是MTVRP配送实际面临的问题。本文针对客户取送双向需求随机性的多行程车辆路径问题，探究实际调整策略和求解算法，旨在为物流企业提供不同于传统情境下实际指导的新思路。

一、问题描述及模型建立

（一）问题描述与假设

本文研究的是三级供应链配送网络中具有随机取送货需求的多行程车辆路径问题，问题情境示意见图1。配送网络中有一个供应商、一个配送中心和多个客户点，采用取送一体化的多行程配送模式，客户需求为同时取送货需求且具有随机性。多行程配送需要作出最优路径决策，确定车辆的初始配送路线方案和实际调整策略，使总物流成本最小。为突出多行程车辆配送的特性，做出如下假设：

假设1 配送网络中的节点连通，配送车辆完全相同，车辆从配送中心出发，完成配送任务之后需要返回配送中心，每辆车仅有一条配送路线，且每条路线上的客户取送货需求总量不能超过车辆最大装载能力；

假设2 假设客户取送货需求服从随机分布，只有当车辆到达该点时其需求才会被确认，取送货物可以进行混合运输；

假设3 初始阶段每个客户点仅能接受一辆车服务，且车辆首次从配送中心出发时均处于满载状态。

图1：MTVRPSPDD问题情境示意图

（二）符号和变量说明

1.参数符号

为便于模型描述，假设配送中心为0，客户集合C={1,2,…,n}，所有点集合V={0,1,2,…,n}，配送中心可用配送车辆集合K={1,2,…,m}，边集合E={(i,j)|i,j∈V}，单位配送成本为cij，车辆最大载重量为Q,单位车辆派遣成本为Ck,客户点i(i∈C)的送货需求si和取货需求qi均是随机变量，服从相互独立的离散随机概率分布，wijk(i∈V,j∈V,k∈K)表示配送车辆k访问客户i之后再访问客户j前的装载量。

2.决策变量

（三）数学模型

根据上述问题的分析、描述及假设，建立相应初始状态的MTVRP优化模型Model I如下。

其中：式（1）为目标函数，最小化车辆派遣成本和配送成本；式（2）-（3）保证任一客户点有且仅有一条车辆配送路线，且同一个客户点之间没有车辆配送路线；式（4）为客户点进出平衡约束；式（5）表示被选中的车辆最多能从配送中心出发一次；式（6）表示只有被选中的车辆才有服务路线；式（7）为支路消除约束，其中S表示车辆k服务的客户集合；式（8）和（9）分别保证每条配送路线上正向配送需求总量、逆向揽收需求总量不超过车辆最大载重量Q；式（10）表示车辆在配送途中的负载量不超过车辆最大载重量Q；式（11）为车辆在服务客户点j后的动态负载量的计算等式；式（12）-（13）表明决策变量为0-1变量。

二、模型转换与求解

（一）随机机会约束规划模型

在模型Model I中，车辆载重约束中含有随机送货需求si和随机取货需求qi，在到达客户点之前无法得知其取送需求的精确值，导致模型无法直接求解，因此需要对Model I进行转换。针对随机变量si和qi，引入随机规划理论生成随机机会约束规划模型Model Π[13-14]。

其中：式（14）中f为物流成本目标函数；式（15）中gi表示Model I中含有随机变量的约束条件即式（8）-（11），α表示预设随机约束条件成立的置信水平，其大小取决于决策者的风险偏好程度，该式子理论上表示事件发生的概率，实际意义是配送路径客户点的随机送货需求量之和和取货需求量之和均不超过车辆最大载重量Q的概率要大于α；式（16）和（17）为已知分布信息的客户随机送取货需求向量；式（18）表示Model I中除了随机约束条件之外的其他约束。

根据随机机会约束规划理论[13-14]，当且仅当Model Π中所有随机约束条件gi(X,si,qi)≤0,i=1,2,…,n均成立的概率大于等于α，则决策变量 X= xijk,yk可行，即路径方案可行。对于随机约束条件组，采用随机模拟技术检验机会是否成立，步骤如下：

Step 1：初始化参数。包括实验次数N，随机约束组gi(X,si,qi)≤0,i=1,2,…,n成立的次数N′；

Step 2：基于需求分布生成随机送货需求矩阵、随机取货需求矩阵；

Step 3：根据随机取送需求矩阵，检验随机约束条件。如果随机约束条件组gi(X,si,qi)≤0,i=1,2,…,n成立，则N′++；

Step 4：重复Step2、Step3共N次；

Step 5：如果N′/ N ≥α，则返回“成立”，否则返回“不成立”。

（二）实时柔性点策略优化路径

在模型Model Π中，Pr{·}≥α表示的是一种概率，即使满足该机会约束生成路径方案，在实际配送过程中仍然会出现线路中断，且取送一体化配送方式增大了路径失败的可能性，故路径需要进行实时调整。在调整策略上现有文献多采用失败点返回策略[15-16]，也有学者研究采取失败点之前提前返回的预补货策略[11]，针对客户的随机双向需求，本文提出基于随机需求分布概率的柔性点策略进行实时调整车辆路径。

假设客户的送取需求分别服从期望为λ1、λ2的随机分布，β表示决策者在随机不确定环境下对某客户点执行配送与否意向的量化，β越大表明决策者对车辆的剩余车载量能够满足下一客户的随机送货需求的要求越高，用Q1j和Q2j表示车辆服务当前客户点j之后的剩余车载量和空余可载货量，且车辆k当前服务客户点j，当Q1j＞0且Q2j≥0时，车辆有两种选择：直接服务下一个客户；返回配送中心补货之后再继续服务下一个客户。

P1为Q1j对应的期望为λ1的随机分布的分布函数值，P2为Q2j对应的期望为λ2的随机分布的分布函数值；若P1≥β，选择方案直接服务初始阶段计划路径的下一个客户，P1越大表明车辆剩余车载量Q1j能够满足下一客户点送货需求的可能性越高。同理，P2也是如此；若P1＜β，车辆剩余载货量Q1j能够满足下一客户随机需求的概率小于β，决策者不能接受这个风险程度，故选择方案返回配送中心补货之后再出发直接前往计划路径中客户点j的后序点进行继续配送。

该多柔性点策略依据车辆实际剩余载货量和实际空余可载货量进行路径选择，由于两者与客户的取送货需求量息息相关，不仅可以避免因客户需求随机导致的盲目性，同时也更能避免不恰当的选择某一返回点情况的产生。

（三）模型求解

多行程车辆路径问题属于NP-hard难题，带有同时取送随机需求的MTVRP模型求解难度增加，禁忌搜索算法通过使用禁忌表和藐视规则可避免算法陷入局部最优，实现全局最优化[17-19]，故采用禁忌算法进行求解。针对Model Π，设计嵌套随机模拟的变邻域禁忌搜索算法（variable neighborhood Tabu Search，VNTS）求解得到优化方案，具体步骤如下：

Step 1：设置算法参数：禁忌长度、禁忌表、算法最大迭代次数、控制最优解未改进最大次数、候选解个数、置信度水平及随机模拟次数。

Step 2：生成初始解。随机产生路径序列，采用解码方案生成初始路径序列Initial_TSP、初始解Initial_Sol，并设置当前路径序列Current_TSP=Initial_TSP、当前解Current_Sol=Initial_Sol。

Step 3：评价初始解。计算Initial_Sol的目标函数值f,若不满足约束条件，则令f=f+M,其中M是一个很大的正数。

Step 4：生成候选解。对Current_TSP进行邻域结构变换，采用解码方案得到候选解集Candidate_Sol。

Step 5：评价候选解。计算Candidate_Sol的目标函数值f,若不满足约束条件，则令f=f+M。

Step 6：更新禁忌表、选取最优候选解Best_Candidate_Sol。

Step 6.1：若Best_Candidate_Sol满足藐视规则，则将其对应的禁忌对象替换禁忌表中最早进入的禁忌对象，同时更新Current_Sol=Best_Candidate_Sol，全局最优解Best_Sol= Best_Candidate_Sol；

Step 6.2：若Best_Candidate_Sol不满足藐视规则，则判断其对应的禁忌对象是否禁忌在禁忌表，若无，则从除Best_Candidate_Sol之外的候选解集中挑选出非禁忌的最优解，用其对应的禁忌对象替换禁忌表中最早进入的禁忌对象，同时更新Current_Sol=Best_Candidate_Sol。

Step 7：终止条件判断。若满足终止准则，输出Best_Sol；否则重复Step4-Step6。

其中，本文采用3种邻域操作进行变换参与算法迭代：insert邻域变换、reverse邻域变换和swap邻域变换，在算法迭代时随机选择其中一种邻域变换方式作用于路径编码，见图2；在考虑目标函数值的情况下，采用基于适配值的藐视规则；算法采用两层嵌套终止准则，外层终止准则为：当迭代次数达到预设值时，算法终止；里层嵌套终止准则为：当前最优解未改进次数达到预设值时，跳出算法终止搜索。

图2：邻域结构变换

三、算例验证与结果分析

（一）实验算例

本文研究的考虑随机同时取送需求的多行程车辆路径问题模型，尚无标准测试算例，故在 Prodhon提出的选址-路径问题标准算例集20-5-1a之上，根据研究内容进行扩展和选取得到本文测试算例。配送中心坐标为(6,7)，该配送中心拥有12台可供配送的车辆，以及20个位置坐标已知、需求未知的客户点。单位车辆派遣成本ck=2500，单位车辆运输成本cv=25，车辆的最大载货量Qv=220。已知在配送开始前存在20个送货需求和取货需求分别服从λ为50和35的泊松分布、位置信息如表1的客户点。

表1：客户节点位置坐标

（二）实验结果与分析

本文应用MATLAB R2014a编程软件进行仿真，VNTS算法参数为禁忌长度table_lengtℎ=20，最大迭代次数max _iter=400，控制最优解未改进最大次数stable_iter=100，候选解个数candidate_count=60。结合算例进行15次仿真实验,并记录每次仿真结果，见表2。

表2：算例仿真结果

由表2可知：

1.若初始目标函数值与实际目标函数值相等，说明在实际配送过程中wijk未超出车辆最大载重量，车辆路径无需进行实时策略调整；若初始目标函数值与实际目标函数值不相等，说明在实际配送过程中存在wijk超出车辆最大载重量，因此车辆路径需要根据客户实际需求情况进行策略调整。

2.在 15次的仿真实验结果中，车辆的实际配送路线与初始优化路径一致的情形只存在少数，因此多数情况下车辆在实际配送阶段需要进行实时策略调整。

随机选取 15次仿真实验结果中某个初始优化方案为例进行分析，选取优化路径方案为车辆 1：0-1-4-18-20-0，车辆2：0-2-17-9-10-0，车辆3：0-11-6-8-19-0，车辆4：0-16-15-14-12-0，车辆 5：0-3-7-5-13-0，总成本为2.2388×104。实际配送过程中，在没有采取任何实时策略的情况下，出现了配送失败的客户点，造成配送路径的中断，中断情况如图3所示。在路线2中，客户点9开始出现路径中断，导致车辆2配送后序客户点10任务失败，在路线3中，客户点8开始出现路径中断，造成车辆3配送客户点19任务失败。

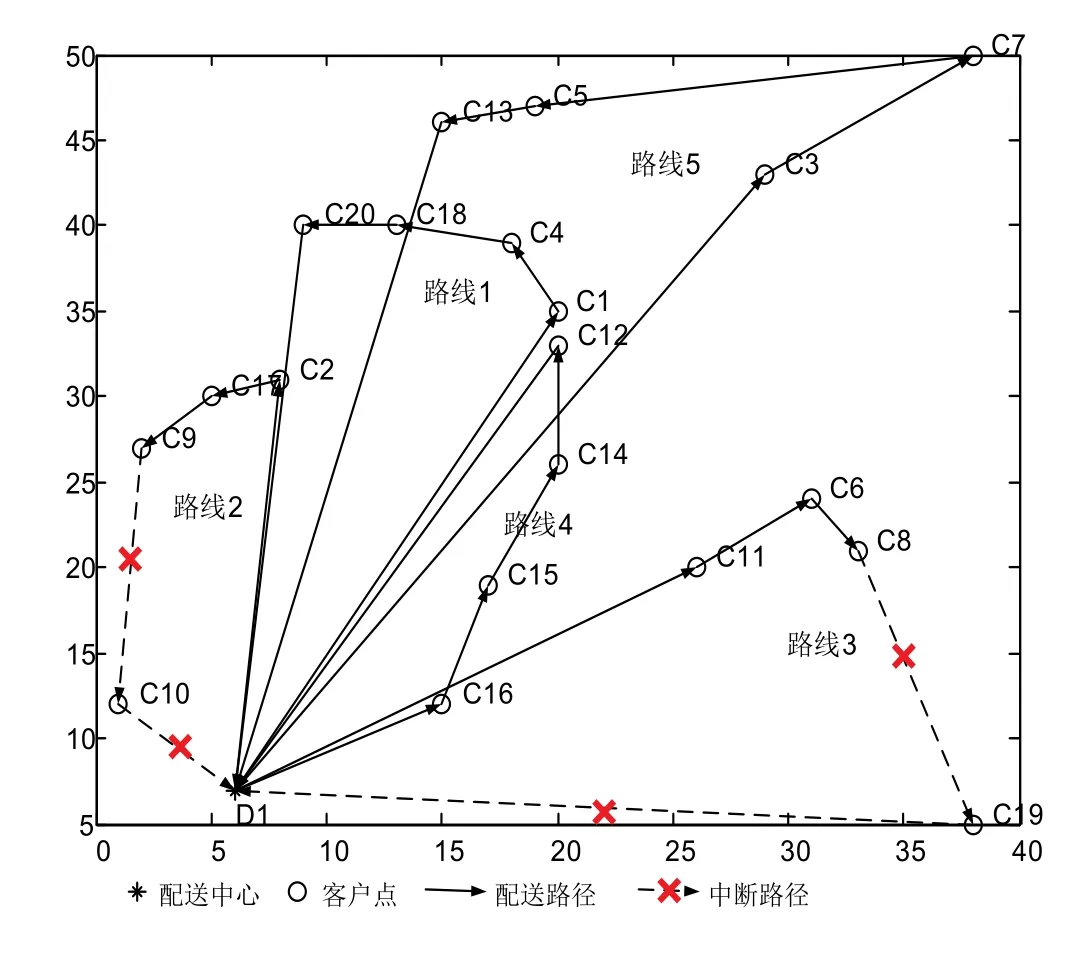
图3 ：配送失败路径图

在实际配送过程中，在采取基于随机需求分布概率的实时柔性点策略的情况下，车辆配送路径如图4所示。调整后路径方案为车辆 1：0-1-4-18-20-0，车辆 2：0-2-17-9-0-10-0，车辆 3：0-11-6-8-0-19-0，车辆4：0-16-15-14-12-0，车辆5：0-3-7-5-13-0，总成本为2.4587×104。

图4：多行程策略调整路径图

初始优化路径是在多种约束下使得总成本最小化的最优路径方案，实时柔性点策略调整的路径方案在初始路径基础上没有产生大幅度的变动，且较于无调整策略下实际配送产生的中断情况，柔性点策略下的多行程路径方案能避免不恰当的返回点，因此，实时柔性点的多行程路径调整策略具有有效性。

四、结论

多行程配送由于允许车辆在运输途中往返，因此有别于一般物流。在多行程配送中，配方考虑同时取送货需求及其随机性，建立多行程配送车辆路径优化模型；针对模型有同时取送、随机参数和多行程动态特征，提出实时柔性点调整策略，引入随机机会约束规则，设计了嵌套随机模拟的变邻域禁忌搜索算法相结合的混合算法寻求最优配送路径。得出以下结论：

1.低成本配送和高水平服务是物流企业的长期目标，考虑同时取送货的多行程物流配送可避免车辆能力浪费，提高配送质量，因此具有较强的现实意义。

2.采用“实时柔性点”多行程路径调整策略，可有效降低因同时取送随机需求造成路径中断产生的额外成本，且避免路径中断，符合实际情境。

3.用随机模拟嵌套禁忌搜索算法相结合的混合求解算法，能有效寻求最优路径，降低无效路径生成的概率。

由于各种因素的存在，现实中的多行程车辆配送网络较为复杂，本文仍存在一些不足之处，如本文并没有考虑到客户信息的多动态性，且配送中心单一，这将是下一步研究的重点。