堤防隐患瞬变电磁三维正演模拟及分析

(长江科学院 水利部岩土力学与工程重点实验室， 武汉 430010)

1 研究背景

堤防是沿河、江、渠、湖、海岸、水库和分蓄洪区等周围修建的挡水建筑物，是抵御洪水、保证人民生命和财产安全的重要工程。但由于堤防线路长、结构复杂、修建年代久远，普遍存在洞穴、裂缝、松散体、高含砂层、渗漏等安全隐患。当遭遇洪水时，存在隐患的堤防极易诱发管涌、漫顶、散浸、滑坡、崩岸、坍塌等险情。及时探查堤防质量状况，消除堤防隐患，是现代水利工程迫切需要解决的技术难题。

堤防隐患探测有其特殊的难点:①堤防线路长，缺乏有效、快速、大范围的查险技术手段；②堤防隐患物理背景的低可探性及堤防隐患物理属性随汛期转换的多变性。目前的堤防隐患探测为静态探测，缺乏多期堤防探测数据的对比，很难完全辨明隐患性状及具体部位，在探测效率、探测精度上也很难做到险情的及时预警。

瞬变电磁法(Transient electromagnetic，TEM)是通过接收地下介质感应出的二次涡流场而达到获得地下电性结构的一种物探方法。利用一个不接地的回线或者接地线源发射脉冲跃阶电流，电流断开的瞬间，目标体在激发场的作用下，其内部会产生感应的涡流。这种涡流与目标体的空间特征和电性特征有关，因为热损耗的缘故会逐渐减弱直至消失。通过观测这种涡流产生的电磁场(二次场)的强弱、空间分布特性和时间特性，达到在时间上由早到晚、深度上由浅到深的勘探目的，从而解决有关工程物探问题。

针对完整堤防坝体电阻率较高、充水性孔洞电阻率较低这一物性特点，可以开展瞬变电磁探测工作。采用瞬变电磁法探测堤防隐患，工作效率高，分辨能力强。

本文首先进行了瞬变电磁三维模型的正演计算，得到了多种堤防异常体的瞬变电磁响应，分析瞬变电磁法对各种堤防隐患的探测效果，并与野外采集的瞬变电磁反演结果进行了对比分析。

2 瞬变电磁法三维正演研究现状

瞬变电磁法具有定位准确、探测深度大、不受地形起伏影响等优点，已经成为一种重要的地球物理勘测方式。瞬变电磁法三维正演方法主要包括有限元法、有限差分法和积分方程法。其中，积分方程法只适合计算比较简单的地球物理模型，而有限差分法计算速度较慢，占用内存大。

1980年，Kuo和Cho[1]研究了三维瞬变电磁时域矢量有限元法的计算，计算了三维低阻异常模型。1987年，Gupta等[2-3]将有限元法和积分方程法结合起来进行瞬变电磁三维正演，在保证计算精度的前提下提高了计算速度，但产生了伪解，并引起边界条件不连续。在瞬变电磁的数值模拟中，麦克斯韦方程推导的电磁场表达式是含零阶或者一阶的贝塞尔函数的积分形式。因为贝塞尔函数不收敛，求解这类积分必须用到汉克尔变换，国内外学者在这方面进行了大量研究。

1997年，Guptasarma和Singh[4]求解了零阶汉克尔变换的61点和120点滤波系数、一阶汉克尔变换的47点和140点滤波系数，提高了计算速度和精度，但瞬变电磁法二次场的计算将异常体作为场源，导致每个测点的收发距都不同，因此，需要重复进行汉克尔变换求解贝塞尔函数，耗费大量的计算时间。1999年，Raiche[5]使收发距与汉克尔滤波系数同步对数等间隔变化，避免了重复计算贝塞尔函数。1999年，Jin等[6]运用标量有限元法和棱边有限元法分别对时间域三维电磁场进行了仿真计算。

2007年，Epov等[7]运用矢量有限元法模拟了三维瞬变电磁场的响应，并且成功将其运用在石油测井中。2008年，Borner等[8]首先采取矢量有限单元法计算出频率域的瞬变场，然后采用余弦变换的方式将频率域的电磁场转化到时间域的电磁场，这样可以很大程度上提高计算效率。2009年，Marinenko等[9]采取矢量有限元法，采取了一阶的矢量基函数进行结构化剖分，二阶的矢量基函数进行非结构化剖分，实现了浅海频率域瞬变电磁的三维正演。2010年，Um等[10]实现了电性源的三维瞬变电磁时域矢量有限元的正演计算，并模拟了海洋三维瞬变电磁场，采用四面体的剖分策略，对含有时间的偏导项进行近似离散，得到电场的方程组，通过解方程得到时间域的电场。

2013年，李建慧等[11]实现了瞬变电磁矢量有限元三维正演模拟，他采取的是结构化的剖分策略，通过异常场法求得频率域的瞬变电磁场，然后通过G-S变换将频率域的瞬变电磁场转换到时间域。2013年，Bakr和Mannseth[12]使用迭代混合解法求解扩散电磁场，该方法先设定一个边界场的初始值，求出内部场，然后根据傅里叶变换求出新的边界场，一直重复这个过程，直到计算结果误差在规定范围内为止。这种算法适用于异常体与围岩的电导率差很小的模型，但当电导率差达200倍时，这种算法精度不高。2014年，Chung等[13]提出了一种基于求解二次磁场的正演方法，克服了基于总场求解只适合于电导率差小的模型的缺点。2015年，Fu等[14]采用矢量有限元法模拟了电性源的海洋三维瞬变电磁场。2016年，张博等[15]采取非结构化剖分策略的矢量有限单元法对带有起伏地形的三维航空瞬变电磁法进行了数值模拟，具体做法是：先采用二次场法求解频率域的电场，然后通过法拉第定律将频率域的电场转换到频率域的磁场，最后通过正弦变换将频率域的磁场变化成衰减电压。

从国内外的研究进展可以看到：先计算频率域的瞬变电磁场，再通过时频转换将频率域的瞬变电磁场转换为时间域的瞬变电磁场的方法繁琐且计算量较大；通过矢量有限元的计算方法，可以直接计算时间域的瞬变电磁场。

3 三维正演计算公式推导

时间域的Maxwell方程为

(1)

式中：E为电场强度;B为磁感应强度;H为磁场强度;D为电位移矢量;J为电流密度;ρ为自由电荷密度。

在各向同性的三维均匀介质中，忽略位移电流，电磁场满足方程：

(2)

式中：μ0为真空中的磁导率;σ为电荷密度；JS为传导电流密度。

对式(2)第1个公式两边取旋度得到

×

(3)

将式(2)第2个公式代入式(3)中得到

×

(4)

在2种介质的分界面，电磁场满足以下边界条件,即

(5)

在无穷远边界，电磁场满足狄利克雷边界条件，在指定值时其旋度为0，即

(6)

采用六面体对异常体和地下介质进行网格剖分，在每个六面体单元内的二次电场近似解为

(7)

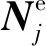
将式(7)代入到式(4)中得到

×

(8)

单元内的余量为

Re=×

(9)

利用伽辽金法，令单元内的余量加权为0，得到

(10)

将式(9)代入式(10)中，可以得到

(11)

将一个单元内的12个形函数全部计算，在每个单元内有

KeEe=Se。

(12)

式中：Ke为12×12阶的单元矩阵;Ee为12×1阶列向量，Ee,Se均为与电流有关的矩阵。对所有单元进行合成，得到

KE=S。

(13)

式中：K为稀疏矩阵;S为与电流有关的向量。将二次电场E分为异常体内部的二次电场Ei和边界二次电场Eb，得到

(14)

式中：Kii为对权矢量和场矢量采用内部棱边形函数得到的刚度矩阵；Kil为对权矢量采用内部棱边形函数、对场矢量采用边界棱边形函数得到的刚度矩阵；Kli和Kll类同;Si为总二次电场。

总场积分方程为

[Kii+Kib(GE2σ-GE1σ)]E=KiiJS。

(15)

式中:Kib为对权矢量采用边界形函数得到的刚度矩阵；GE1σ和GE2σ分别为一次电场和二次电场的格林函数。求得一次电场强度后，根据下式可以求出二次磁场强度，即

(16)

式中：Hi(r)为一次磁场强度；GH2为二次磁场的格林函数。

4 三维正演算例分析

为深入认识堤防不同隐患的电磁场分布特征，本文开展了典型堤防隐患的瞬变电磁数值模拟计算。由均匀半空间解析解和层状介质数字滤波解的理论公式，推导出均匀半空间激发源在时间域电磁场各分量的表达式。基于非均匀剖分方式的有限元(FEM)正演方法，研究了正演的基本方程、网格划分形式、迭代格式、稳定性条件、边界条件、源的激励形式等。通过构建堤防数值模型，正演计算堤防模型的瞬变电磁场响应，并在堤防模型中设置不同形状和类型柱状、板状、复杂电性异常体，通过对抽取断面的电场和磁场的分布来研究含隐患异常体堤防模型的瞬变电磁场响应特性和规律。具体计算结果如下：

(1)算例1。如图1(a)所示，坝体长为20 m，宽为10 m，高为10 m，坝体电阻率为500 Ω·m，供电线圈边长为1 m，匝数为1，供电跃阶电流为40 A(从t=0 s开始供电，供电持续0.5 ms后断开)，线圈正下方5 m处有一低阻球体(电阻率为10 Ω·m)。

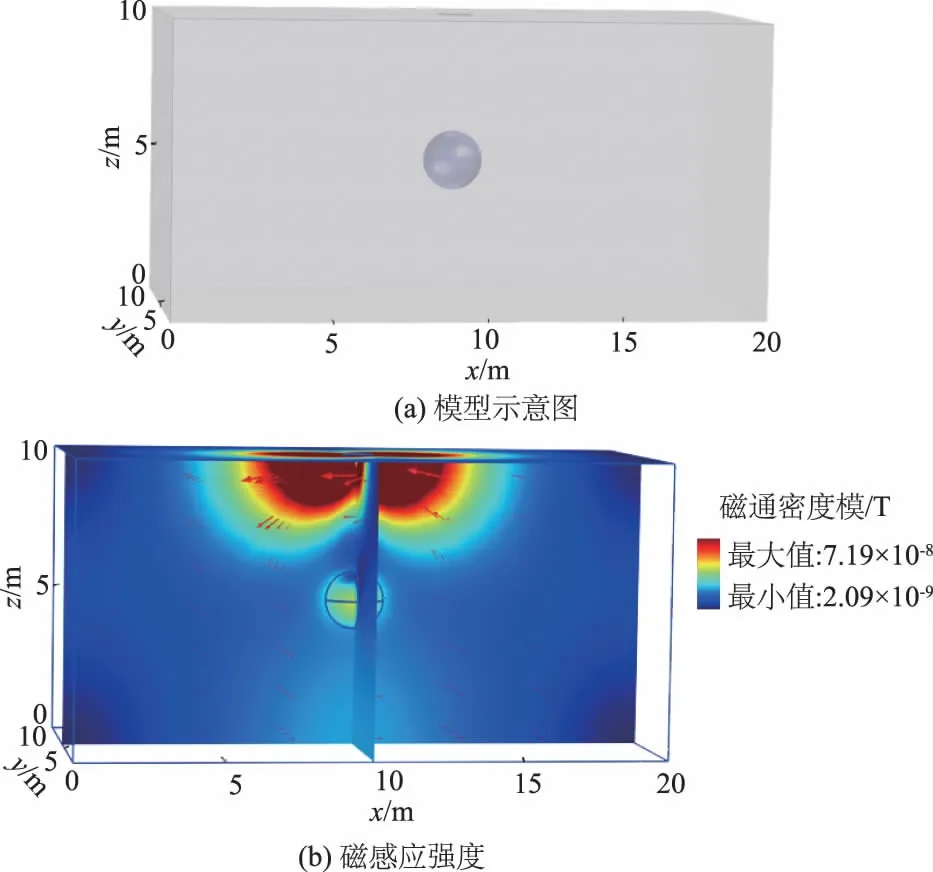
图1 算例1模型示意图及磁感应强度

算例1正演计算的响应时间为100 ms，正演计算可以得到瞬变电磁的波场快照，截取传播时间为0.04 s时的波场如图1(b)所示，体箭头表示磁通密度方向。从图1(b)可以看到，低阻区域的磁感应强度呈现明显异常，异常区域与低阻球体位置吻合良好，表明瞬变电磁法可以对低阻体进行有效勘察。

(2)算例2。堤防模型与算例1类似，线圈下方5 m处存在孔洞(视为高阻球体)。坝体长为20 m，宽为10 m，高为10 m，坝体电阻率为200 Ω·m，供电线圈边长为1 m，匝数为1，供电跃阶电流为20 A(从t=0 s开始供电，供电持续0.5 ms后断开)，线圈正下方5 m处有一孔洞(模拟空洞，电阻高)。正演模拟截取0.04 s处的磁场快照如图2所示。

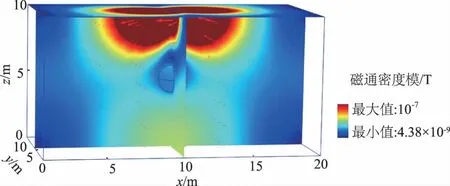
图2 算例2的磁感应强度

由图2可以看到，孔洞区域磁感应强度异常不明显，同时，在孔洞下方形成了假异常。可见当坝体本身电阻率较高时，瞬变电磁法对堤防孔洞的分辨能力较弱。

(3)算例3。如图3(a)所示，坝体长为20 m，宽为10 m，高为15 m，坝体电阻率为500 Ω·m，浸润线位于坝高5 m处，浸润线以下部分坝体电阻率为50 Ω·m，供电线圈边长为1 m，匝数为1，供电跃阶电流为20 A(从t=0 s开始供电，供电持续0.5 ms后断开)。截取0.04 s的磁场波场快照，显示结果如图3(b)所示。

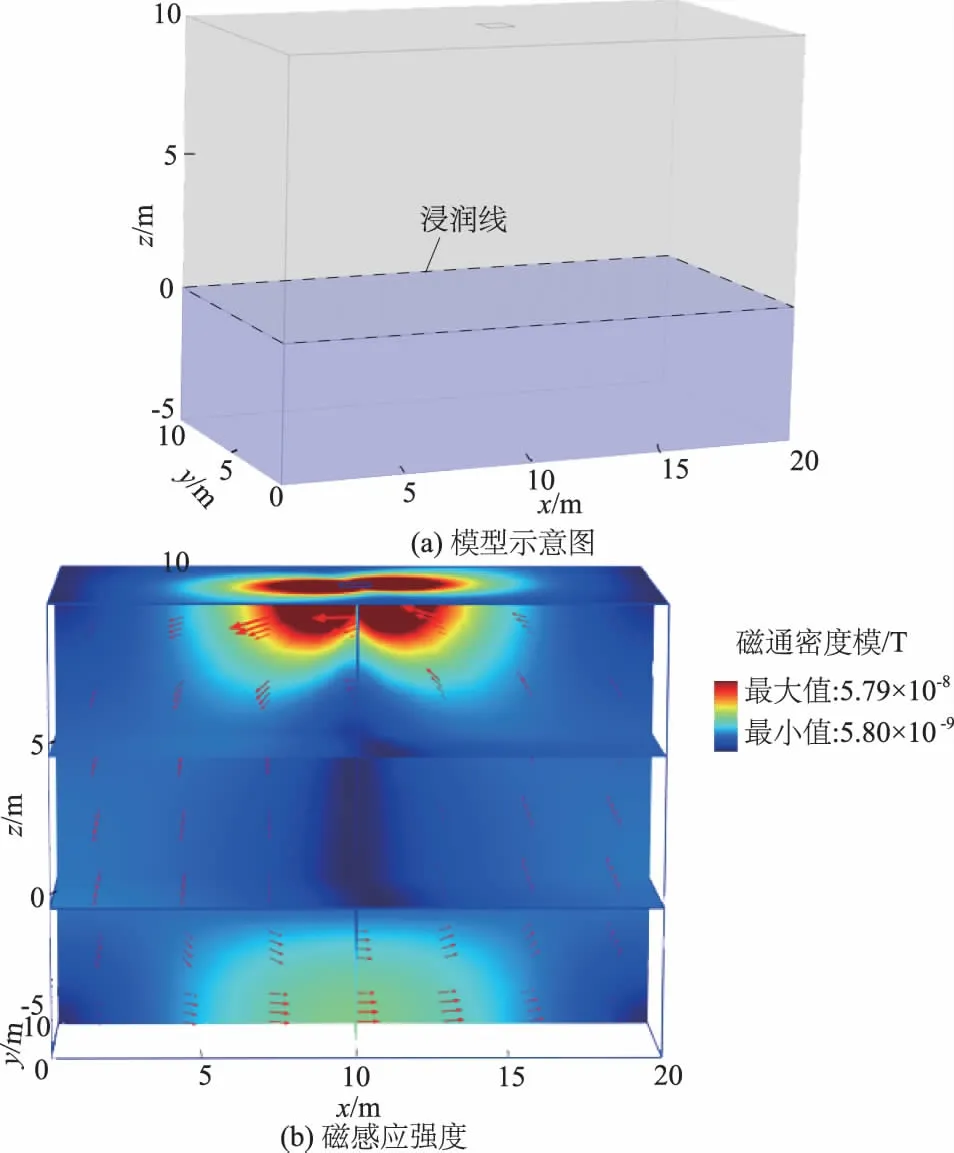
图3 算例3模型示意图和磁感应强度

浸润线以下的坝体电阻率较低，与浸润线上部的坝体电阻率有显著的差异，三维正演结果准确地反映了浸润线的位置。

(4)算例4。如图4(a)所示，坝体长为20 m，宽为10 m，高为10 m，坝体电阻率为500 Ω·m，供电线圈边长为1 m，匝数为1，供电跃阶电流为40 A(从t=0 s开始供电，供电持续0.5 ms后断开)，线圈正下方5 m处有一低阻渗流通道(电阻率为50 Ω·m)，相应的t=0.04 s时的磁场响应快照如图4(b)所示。

图4 算例4模型示意图和磁感应强度

渗流通道整体为低阻，三维正演结果反映了渗流通道的位置，但渗流通道尺寸较小，异常较弱。

(5)图5为重庆某灰岩地区的瞬变电磁勘察结果。该测区基岩为高阻灰岩，瞬变电磁结果与现场地质条件一致，同时，电阻率反演结果推测了几处岩溶较发育区域。后续的钻孔结果与瞬变电磁勘察结论吻合较好，验证了瞬变电磁法对高阻围岩中的低阻体有很强的分辨能力。

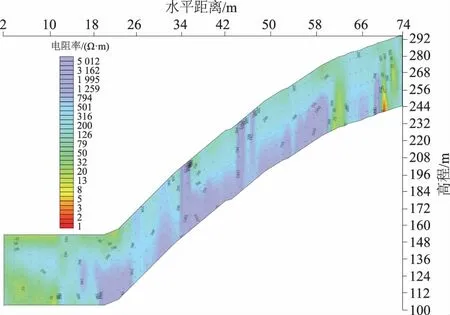
图5 瞬变电磁实测数据反演结果

从不同堤防隐患的瞬变电磁场正演结果和实测数据反演结果可以发现，瞬变电磁法对低阻体敏感，对不同形态的低阻异常体探测效果均较好，因此采用瞬变电磁法进行堤防隐患快速普查的研究思路是可行的。

5 结 论

瞬变电磁法具有施工效率高，无地形影响等特点，通过本次三维模型计算和现场资料的采集和处理分析，可得出以下结论：

(1)瞬变电磁法三维正演方法主要包括有限元法、有限差分法和积分方程法。其中，有限单元法可以解决非线性不规则区域问题，能计算各种复杂模型，为瞬变电磁三维正演计算的有效方法。

(2)对比三维正演结果和野外实测数据反演结果可以发现,瞬变电磁法对充水孔洞、渗流通道和浸润线等低阻体分辨能力很强，对高阻体的分辨能力较弱。充水洞穴、裂缝、渗漏等安全隐患普遍存在于我国的中小型堤防中，因此，采用瞬变电磁法对此类堤防进行隐患勘查是十分有效的。