椭圆形变微小水滴撞击深水液池运动大型气泡夹带机理*

裴传康 魏炳乾 左娟莉 杨泓

(西安理工大学,省部共建西北旱区生态水利国家重点实验室,西安 710048)

在微小水滴撞击深水液池运动中,水滴在下降过程中产生的外形振荡对后续空腔产生及气泡夹带有极大影响.因此,本文假定5种不同宽高比(AR)的微小变形水滴,采用自适应网格技术和体积函数方法对其运动过程进行数值模拟,并详细探究不同撞击速度和水滴形变对撞击后空腔变形坍缩过程、涡环的发展以及气泡夹带的影响.研究结果表明,在较高撞击速度下(Fr=112.5,We=145,Re=1740,Vi=6 m/s),AR=1.33下的长椭圆形变水滴与液池聚合并产生大型气泡夹带.大型气泡截留过程主要由水滴撞击时颈部自由面下产生的涡环控制,涡环裹挟自由界面形成滚动射流,最终射流接触夹带大型气泡.在气泡截留后期,腔内气旋推动侧壁向外拓展,有效增大了气泡体积.在撞击初期阶段,液滴形状越扁,水滴与液池颈部射流曲率越大,生成涡环强度越大.但扁椭圆水滴生成涡环距离自由面过近,界面的早期拉动破坏了涡环强度,因此涡环衰减也相对较快.

1 引 言

液滴动力学是流体力学多相流领域的重要研究分支之一.认识液滴在不同介质、组分及形态下的运动及变形过程能够促进对气液交换现象的深入理解[1,2].水滴撞击不同介质的运动作为流体力学中最为人熟知的典型流动现象之一,由于其在工业应用及阐释相关自然现象中的重要价值被广泛研究[3-6].作为一种普遍存在的自然掺气过程,水滴在大面积水体中的聚并及其撞击水体产生的空腔运动是自然界气液交换的主要途径之一,对于水下声音传播、水生生物、水体生态环境以及化学反应过程等具有重要的意义[7,8].

自1963年Worthington[9]首次系统地对液滴撞击进行探索以来,诸多学者对液滴撞击不同介质时气泡夹带的复杂物理过程进行了大量的物理实验及数值模拟研究,结果表明在液滴撞击液池时,气泡夹带主要以两种方式产生：一种是由于液池空腔坍塌闭合,在空腔底部夹带一部分空气形成气泡[10].另一种是由于液滴底面包裹的空气膜破碎造成[11,12].Pumphery和Elmore[13]通过实验改变撞击速度和液滴直径首次定义了大型气泡夹带现象,认为液滴撞击产生气泡夹带只在一个十分狭小的物理范围内发生,Oğuz和Prosperetti[2,14]对液滴撞击深水液池时气泡在不同液滴振荡形状及初始速度下的产生和溃灭做了较为详尽的研究,他们利用韦伯数和弗劳德数描述了特定情况下气泡夹带发生的上限和下限(Weu=48.3Fr0.247,Wel=41.3Fr0.179),并首次采用边界积分法数值模拟了气泡夹带和空腔运动,认为在常规气泡夹带上限之上的状态下,空腔底部会在气泡夹带行为发生前反转运动方向,并在空腔中心生成一个短而粗的射流.Oğuz和Prospretti[15-17]还对液滴撞击液池时水下噪声的产生与大型气泡夹带的关系做了详尽的探索.Deng等[18]研究了液体黏度及表面张力对液滴撞击的影响,并观察到夹带气泡的大小随Ca数的增大而减小,而黏度的增加同样增大了液滴进入液池的流动阻力,使得规则气泡夹带区域的上限增大.Chen和Guo[19]进一步探讨了液体黏度对常规气泡夹带产生的影响,并导出了Ca数与气泡大小分布的相关函数.

以往对水滴撞击深水液池的研究多假定液滴撞击形态为球形,而事实上,在微小水滴撞击深水液池的过程中,水滴在运动状态、表面张力及周围介质等多方面的作用下产生的变形和界面振荡周期对后续空腔产生及运动行为有极大影响[20].液滴在不同速度、尺寸、周围气体及初始温度环境下自由坠落的变形过程,在典型应用中受到广泛关注[18,21-25].丁思源等[26]对不同表面张力下液滴在自由落体过程中的形变规律进行了探索.Lamb等[7]研究了液滴下落的振荡,并通过极坐标系中相关的勒让德多项式(Pn)描述了液滴跌落随时间外形的变化.Roman和Bico[27]通过实验研究表明,水滴在坠落过程中形状随坠落时间呈两种不同的周期性变形模式,且水滴的初始速度和直径与液滴形状及其振荡周期有较强联系.Thoroddsen等[10]则通过高速摄影机探究了不同形状水滴撞击下空腔底部产生的微小气泡夹带现象,并认为圆柱形空腔底部出现的微小气泡是由于射流径向流动引起的局部空化造成的.

目前研究较少关注直径在微米层级的微小变形水滴撞击静止深水液池时的大型气泡夹带现象及发生条件,微小水滴撞击深水液池的气泡生成与液滴变形幅度的关系也有待进一步探究.基于此,在前文研究基础上[28],本文假定5种不同椭圆形变的微小水滴,采用能够精确捕捉自由表面的开源多相流程序Gerris对不同程度椭圆形变下微小水滴撞击深水液池运动进行二维数值模拟,深入探究不同初始撞击速度和初始形状下微小水滴撞击深水液池的大型气泡夹带规律.

2 数值方法与计算区域

2.1 控制方程

不可压缩、可变密度、带有表面张力项的Navier-Stokes (N-S)方程可以用来描述液滴撞击的气液两相流动[29,30]：

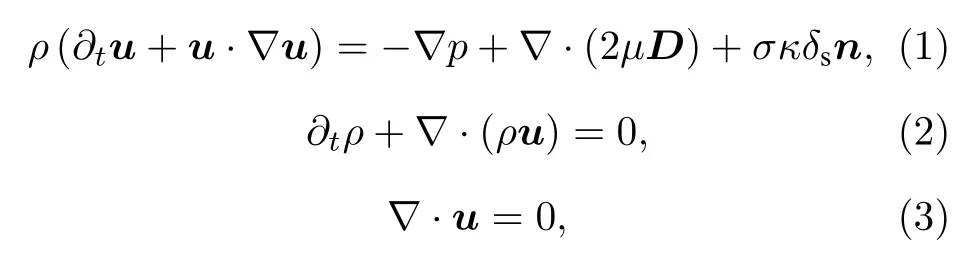
式中 ρ=ρ(x,t) 为流体密度,u=(u,v,w) 为流体速度,p为压力,µ=µ(x,t) 是流体的动力黏度,变形张量 D 定义为 Dij=(∂iuj+∂jui)/2 ,σ 为表面张力系数,κ 为界面曲率,狄拉克分布函数 δs表示表面张力仅作用于两相界面处,n 为两相界面的法向量.

Gerris采用经典的VOF方法追踪相界面,对于两相流动,引入计算网格中第一种流体的体积分数 c(x,t) ,并定义混合流体的密度和黏度为：

式中 ρ1,ρ2,µ1,µ2分别是第一种流体和第二种流体的密度以及黏度; 函数由体积分数c平滑处理后得出,以便提高计算的稳定性.

密度对流方程可由等效的体积分数对流方程替换,即

2.2 数值方法与网格划分

由于液体相的高离散程度、几何的复杂性及流动特征尺度间的巨大差异需要足够网格分辨率来表示,因此对于高速运动微小液滴的撞击及溅射过程进行直接数值模拟十分具有挑战性.采用自适应网格细化(AMR)方法可以较好地解决该类物理问题的数值模拟.AMR技术中的网格可以根据流动特征(例如界面位置、变量的梯度变化等)进行局部细化或粗化,将计算效率集中在最需要的区域,从而以较低的计算成本实现精确的数值模拟.

本文采用开源代码Gerris进行数值模拟,该代码使用基于笛卡尔网格的有限体积法和基于四叉树/八叉树的自适应网格技术来求解控制方程,利用基于分段线性界面计算的VOF方法(PLIC/VOF)用于跟踪相界面[29,30].在本文数值模拟中,针对水滴撞击深水液池运动的特性,以体积分数、计算域的速度场和涡量场作为主要自适应条件,动态加密水滴与液池相界面处的网格至最大层数.计算一步,动态更新一次计算网格,其中最大网格加密层数为13层,即在一个计算区域(box)内的最大网格数量为213.椭圆形变液滴在撞击深水液池下落过程中,由于液滴界面形态并非完美的正圆形,因此界面稳定性相对正圆形液滴较差.所以在初始计算时即对液池与液滴相界面处正负0.3,Y向液滴中心上方2r至水面下方6r,X向对称轴左右6r内的矩形内进行加密,以保证计算的稳定性.

2.3 计算条件

对计算域进行轴对称数值模拟,对称轴设为Y轴,即Y轴边界为可自由滑动、无流体进出、不可渗透的对称边界.上边界设为自由出流边界,下边界及右边界设为无滑移边界.水滴的椭圆变形可由宽高比(AR)来表示,定义为

式中a和b分别为水滴的横向及纵向直径.AR＞1代表长椭球体,AR=1代表球体,AR ＜ 1代表扁椭球体.如图1所示,本文设定5种不同初始形状的水滴进行计算,AR分别为1.33,1.16,1,0.84,0.67.

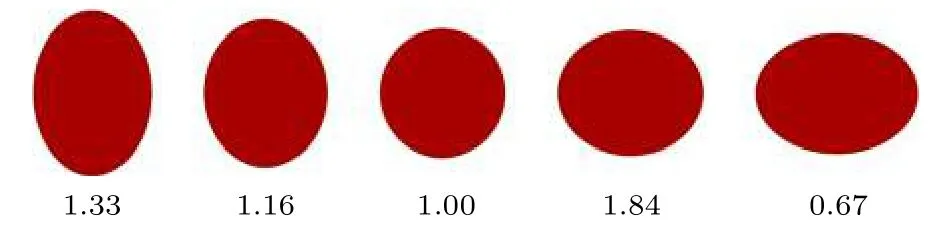
图1 各工况下水滴几何形态Fig.1.Water droplet geometry in different cases.

定义椭圆液滴的同等直径为

如图2所示,本文数值模拟将不同椭圆形变下的水滴初始化在液池上方0.1D处,初始撞击速度为 Vi.计算区域长20D,宽10D,液池深度为12D以保证边界不会对液滴撞击液池运动产生影响.水滴在重力g及初始撞击速度 Vi的作用下垂直进入液池.水的密度为1000 kg/m3,动力黏度为1×10-3Pa·s,表面张力系数为0.072 N/m,空气的密度为1.21 kg/m3,空气的动力黏度为1.81×10-5Pa·s.

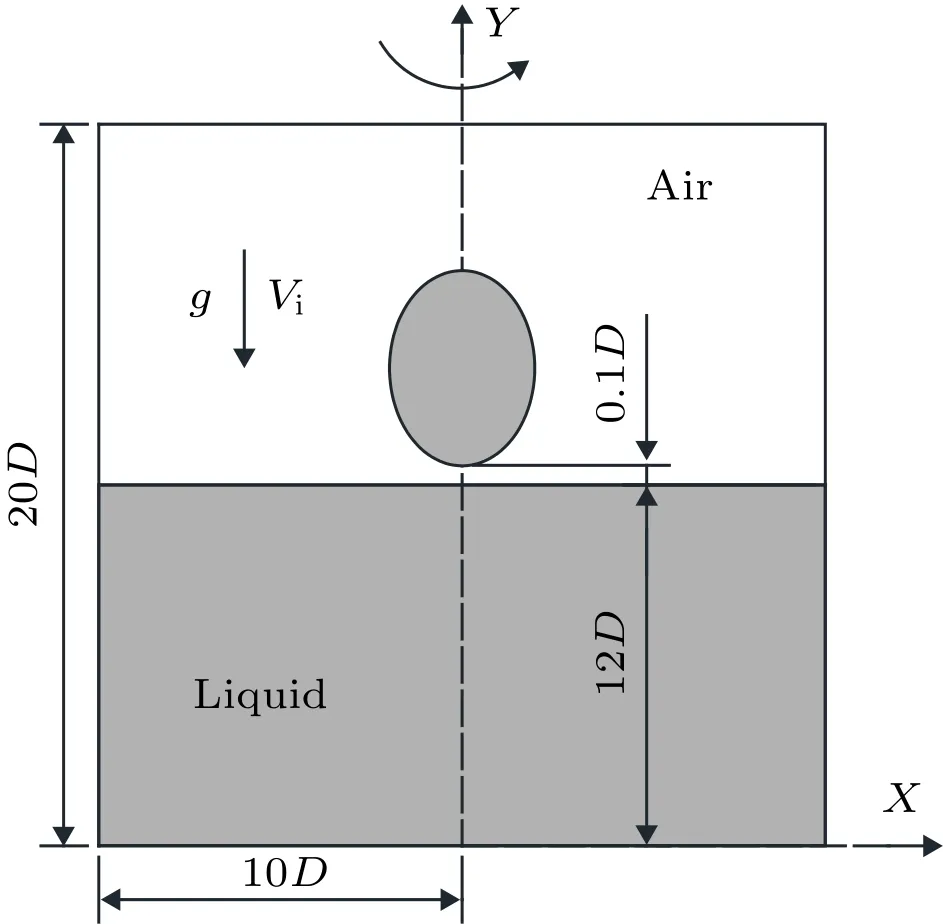
图2 计算区域简图Fig.2.Schematic diagram of the computational domain.

采用雷诺数(表征液体惯性力与黏滞力间的关系)、韦伯数(液体惯性力与表面张力间的关系)和弗劳德数(液体惯性力与重力间的关系)来描述液滴撞击的运动特征,3个无量纲参数的表达式如下式所示：

2.4 模型验证与率定

文献[28]已对本文数值方法在圆形水滴撞击深水液池数值模拟中的适用性与准确性做了详细的对比与率定.本文采用不同AR的椭圆型水滴进行数值模拟,为了保证椭圆形变水滴撞击深水液池数值模拟所得空腔运动及气泡夹带大小结果的准确性,选择Thoraval对变形液滴大型气泡夹带的实验数据进行模型验证[31].图3所示照片为高速摄影机实验摄得自由液面随时间的运动过程,左下角线段代表1 mm长度单位,图示时间从左到右分别为液滴接触水面后-1.3,5.4,7,11和20 ms,无量纲时间分别为-0.34,1.4,1.82,2.86,5.2.实验使用同等直径为5.0 mm的10.5%的MgSO4液滴以1.30 m/s的速度撞击液池,液滴黏度为1.96 cP(1 cP=10-3Pa·s),密度为1.105 g/cm3.撞击时液滴AR为1.33.弗劳德数及韦伯数分别为Fr=34.5,We=116.7.

图3 实验摄得自由液面随时间运动过程[31]Fig.3.Experimental image of free surface movement at selected times[31].

图4为数值模拟自由液面随时间的运动过程.模拟物理参数与Thoraval等的实验参数相同,右下角白线代表与实验相同的1 mm长度单位.对比图3与图4可知,液滴垂直进入深水液池后,首先激发出环形卷曲射流,射流向下运动,并在射流下方生成了一个巨大的空腔.随后两侧射流在空腔中心碰撞并形成巨大的气泡夹带.数值模拟结果在空腔闭合前相较实验稍慢,但在闭合后产生中心射流的速度却相对较快,且在液池液面上方也产生了细长的中心射流,并夹断生成多个二次滴.这种情况的产生可能是由于实验液滴在接触液池时刻形状难以控制,而本文数值模拟只能对该时刻液滴形状作椭圆近似处理,数值模拟初始条件无法与实验完全匹配而导致的.但本文采用的数值方法较为正确地预测了液滴撞击深水液池空腔的成长过程以及气泡夹带现象,基本物理现象吻合良好.数值模拟所得气泡内部中心射流穿透气泡时气泡宽度及穿透深度相对实验结果的误差分别为1.1%和5.7%,表明数值模拟能够大致地描述椭圆形变液滴撞击深水液池时的大型气泡夹带现象.

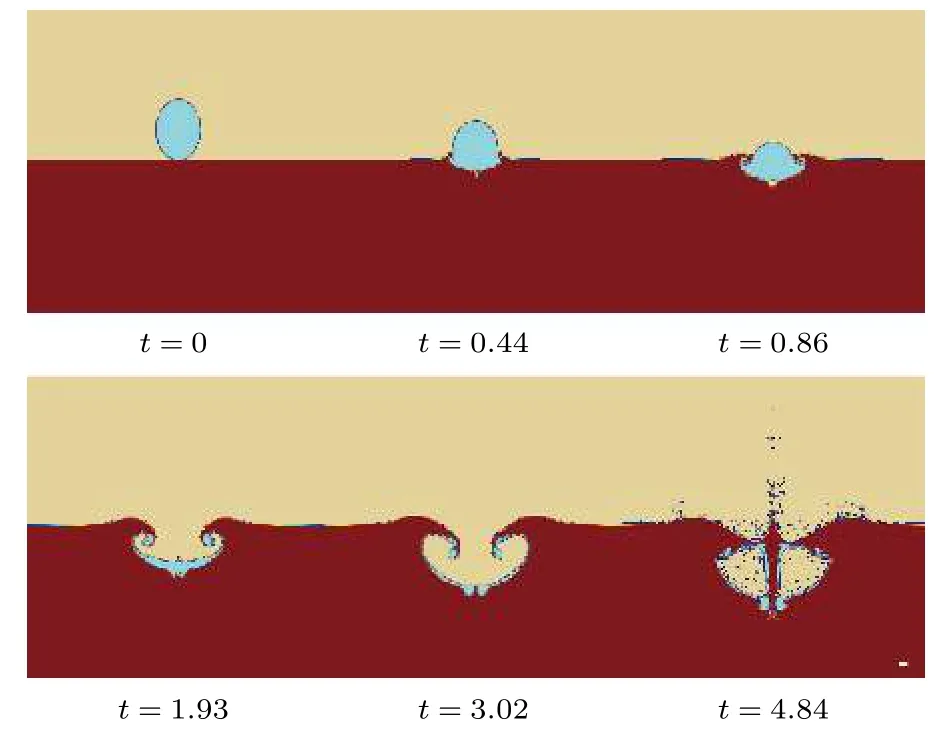
图4 数值模拟自由液面随时间运动过程Fig.4.Numerical simulation of the free surface movement at selected times.

3 计算结果与分析

3.1 不同速度下水滴撞击液池的聚合过程

为探究不同形变和撞击速度下水滴撞击作用对深水液池相界面变化、水滴与V池水的混掺过程以及撞击所夹带的气泡大小的影响,首先使用经过验证的数值方法研究同等直径为290 µm的水滴在重力的作用下以4 m/s的速度垂直下落并撞击深水液池的运动过程.以下全文涉及的所有长度单位均为实际长度除以参考长度 D∗后的无量纲长度,时间t为实际时间乘以 Vi/D∗后的无量纲时间.

水滴以3种不同AR和4 m/s的撞击速度进入深水液池后,自由表面的界面变形以及水滴在液池内的混掺分布如图5所示,Fr=75,We=64.4,Re=1160,Vi=4 m/s.为了考察液滴在液池内的混掺情况,给定水滴部分液相天蓝色示踪和液池部分液相红色示踪.从工况(a)到(c),水滴的AR依次减小.在图5(a)中,水滴以AR=1.16的长椭圆形变撞击深水液池,与液池发生完全聚合现象,且无气泡夹带现象发生.撞击生成的空腔在初始阶段呈内凹形,随时间增加逐渐向V形演变.撞击发生时自由面的变化较为平缓,使得水滴入水后基本附着在自由液面之下.随着时间增加,空腔开始向底部运动,带动水滴部分的水体向中心聚合并产生两个对称的涡结构.

在图5(b)中,正圆形水滴(AR=1)撞击产生的空腔与长椭圆形相比,空腔内凹程度降低,水滴和深水液池水体混掺情况与长椭圆形相仿,无气泡夹带的现象发生.在图5(c)中,水滴以AR=0.84的扁椭圆形垂直下落并撞击深水液池,其达到最大空腔深度所用时间在3种工况中最短,在中心射流形成时,所用时间也相对较短,毛细波向底部运动的速度相对较快,因此水滴部分水体在原空腔侧壁处形成的涡结构尚未完全向中心处靠近.对比3种工况可知,扁椭圆形水滴入水后对水滴部分水体的涡结构生成有较强的抑制作用,而长椭圆形水滴引发的自由面变化相对较大,生成中心射流所用时间也较其余两工况长.

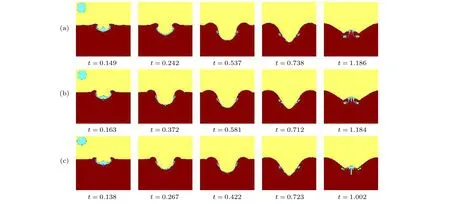
图5 不同工况下自由液面随时间的运动过程(Fr=75,We=64.4,Re=1160,Vi=4 m/s) (a) AR=1.16; (b) AR=1.00;(c) AR=0.84Fig.5.Free surface profiles with simulated at selected times (Fr=75,We=64.4,Re=1160,Vi=4 m/s)：(a) AR=1.16; (b) AR=1.00;(c) AR=0.84.

选取水滴以5种不同AR形变及6 m/s的速度撞击深水液池,并探究在此种较高速度下水滴形变对气泡夹带的影响.水滴以5种不同宽高比和6 m/s的撞击速度进入深水液池后自由表面的界面变形以及水滴在液池内的混掺分布如图6所示,其中Fr=112.5,We=145,Re=1740,Vi=6 m/s.从工况(a)到(e),水滴的AR依次减小.在图6(a)中,水滴以AR=1.33的长椭圆形变撞击深水液池,与液池发生完全聚合,并产生大型气泡夹带现象.撞击生成的空腔在初始阶段呈内凹形,且两侧环状射流在液滴与液池接触颈部涡旋的带动下向空腔中心滚动.随着时间的增加,两侧的滚动射流在空腔中心交汇,形成一个较大的气泡夹带,滚动射流在空腔中心处碰撞,在强烈的动能作用下生成垂向的中心射流.最终向下的中心射流底部颈部断裂,在空腔内部生成一个悬浮的二次小水滴.整个运动中液池部分相界面变化较为剧烈,涡旋的形成与发展在空腔运动及气泡夹带中起到了至关重要的推动作用.

在图6(b)中,AR=1.16的长椭圆形水滴撞击产生的空腔与AR=1.33的工况(a)相比,在运动形态上有很大不同.在工况(b)中,由于初期水滴与液池颈部产生的涡旋强度相对较低,无法有效带动两侧环状射流向空腔中心滚动,空腔开口处内凹程度较低.随着时间增加,空腔逐渐向U形变化,并最终变为倒梯形,在空腔底部形成一个近乎于腔底垂直的尖锐界面,推动空腔底部部分侧壁坍缩闭合,截留形成一个较小的气泡.液滴部分液体分离成两部分,一部分随自由面变化在液池自由面下形成较小的涡旋,另一部分则附在空腔侧壁,空腔坍缩后随夹带气泡向液池底部运动.图6(c)至图6(e)这3种工况中,水滴在撞击液池后形成的空腔形态与气泡夹带与工况(b)非常近似.在工况(c)中,水滴以正圆形垂直下落并撞击深水液池,无任何大小气泡夹带发生.而在工况(d)与工况(e)中,由于水滴以扁椭圆形撞击液池,水滴在进入深水液池后一直较为平坦地附着在深水液池自由面以下,并没有在二者接触面生成较强的颈部涡旋.最终空腔变化形态与正圆形液滴较为相似,但空腔底部仍旧产生了尖锐的垂直界面,截留成为一个较小的气泡,分离出的上部分水滴相由于没有涡旋生成,呈扁平状分布于液池自由面以下.

图6 不同工况下自由液面随时间的运动过程 (Fr=112.5,We=145,Re=1740,Vi=6 m/s) (a) AR=1.33; (b) AR=1.16;(c) AR=1.00; (d) AR=0.84; (e) AR=0.67Fig.6.Free surface profiles simulated at selected times (Fr=112.5,We=145,Re=1740,Vi=6 m/s)：(a) AR=1.33; (b) AR=1.16; (c) AR=1.00; (d) AR=0.84; (e) AR=0.67.

对比上述工况可得,大气泡的夹带受到水滴与液池颈部微小射流以及涡旋出现的限制.颈部涡旋的出现取决于水滴的撞击速度与撞击形态.大型气泡的截留可归功于由涡环形成的滚动射流在空腔中心处的合并.涡旋流的强度必须足够大,以便形成向中心处运动的细长滚动射流.如工况(b)所示,如果涡旋流的强度不够强,那么滚动射流虽然出现,却无法在空腔中心处相遇碰撞,因此无法获得大型气泡夹带.在图6(c)中,对于AR=1.00,撞击速度为6 m/s的正圆形液滴,虽然出现了颈部涡旋,但它没有充分发展伸长,因此并没有在空腔中心轴处合并.

3.2 大型气泡夹带机理

选取变形水滴与深水液池撞击并产生大型气泡夹带的工况(a)对大型气泡夹带机理及其空腔运动进行更加深入地研究.图7为不同时间节点下AR=1.33的长椭圆形变水滴撞击深水液池的等值线图,图7中左侧示意涡量场,右侧示意压力场,黑色实线代表液面运动的相界面.由涡量场可知,在撞击初期,涡旋仅在水滴与液池接触颈部产生,且位置接近自由表面.随后在t=0.102时,涡旋逐渐拉动自由表面进行卷曲运动,自由表面曲率逐渐增大,并于t=0.195左右产生滚动射流.滚动射流在空腔中心轴线处合并,并在液池内产生大型气泡夹带.由此可得,大型气泡截留过程基本由水滴撞击深水液池时产生的涡量控制,长椭圆形的水滴形状改变了自由表面下生成涡环的强度以及其与界面的相互作用.在其拉动界面之前,在液池中垂向移动较深,具有较强的穿透性,涡环的影响范围增大,使得空腔侧壁处液池液体向远处移动,空腔上部界面被裹挟形成滚动射流,最终射流接触合并以夹带大型气泡.

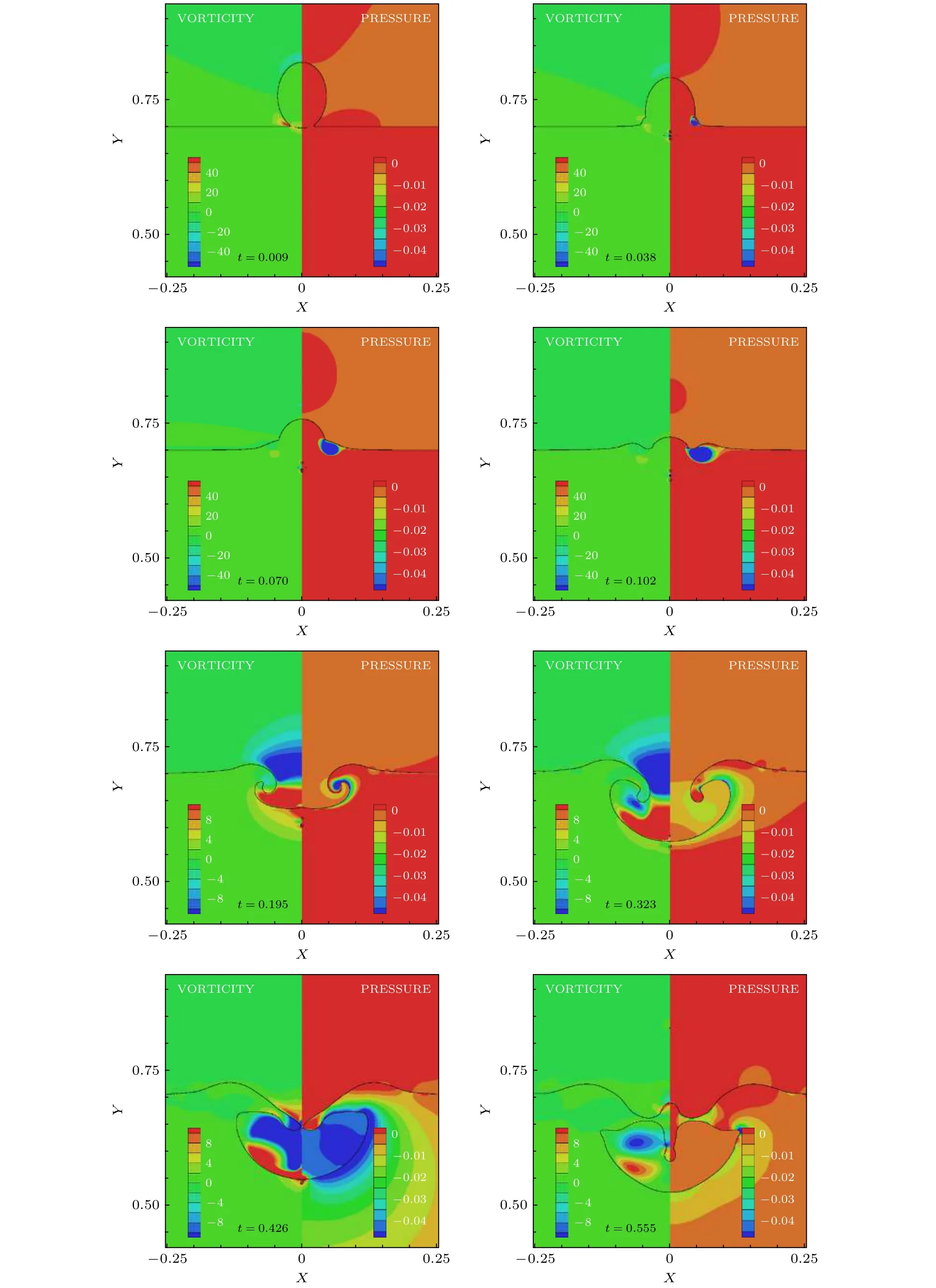
图7 不同时间节点下长椭圆形变水滴撞击液池涡量场和压力场等值线图(Fr=112.5,We=145,Re=1740,Vi=6 m/s,AR=1.33)Fig.7.Vorticity and pressure contours of a prolate water droplet impacting into a water pool at selected times (Fr=112.5,We=145,Re=1740,Vi=6 m/s,AR=1.33).

由前文研究可知[28],在水滴撞击深水液池时,空腔在涡环和毛细波的驱动下运动并坍缩.而毛细波的传播与运动可以由液池内负压区的分布来间接示踪[32].图7右侧给出了不同时间点下AR=1.33的长椭圆形变水滴撞击深水液池的压力场负压区示意.由图7可知,在颈部射流出现后,毛细波驱动的界面由于局部压力下降较大而形成尖锐的外角.当射流边缘与液池表面合并并向下运动时,界面曲率及加速度随之增加,射流边缘向下流动,毛细波将波上方的高压区与下方低压区分开,随后,上方高压区导致空腔的变形,而毛细波前后的压差导致液体流动速度加快,增强了毛细波的传播速度.在t=0.195时,涡环驱动的滚动射流形成,负压区也集中分布于滚动射流内壁,与涡环作用部位十分相似.其后界面曲率不断缓和,负压区范围及强度也逐渐减小,毛细波位置不断随空腔运动向空腔底部传递,并和滚动射流发生碰撞.产生大型气泡夹带后,负压区集中于气泡内部的尖锐界面处,此时初始颈部涡环对界面运动的影响逐渐减弱.综上所述,在长椭圆形水滴撞击液面初期,毛细波运动一直跟随涡环的运动,并沿着空腔侧壁向下传播,对空腔形态的塑造和滚动射流的产生起到了一定的影响,是大型气泡夹带的重要因素之一.

图8为不同时间节点下AR=1.33的长椭圆形变水滴撞击液池的速度场等值线图和速度矢量分布图.图8中黑色实线条为两相界面,为了便于分析和观察,速度矢量取层级为6及以下的网格显示.由图8可得,在滚动射流产生后不断向空腔中心轴线处运动,使得空腔开口缩小,此处空气收到挤压,速度不断增加,夹带入空腔的气体在滚动射流相界面曲率的影响下开始产生涡旋运动.在t=0.323后,空腔内气体涡旋逐渐形成,并参与了空腔运动过程,使得空腔侧壁处不断向外扩展,腔内气体最终在滚动射流碰撞闭合后开始在气泡内循环流动,带动气泡不断向下运动.由此可见,在气泡截留后期,空腔内的气体也参与了空腔运动的过程,推动空腔侧壁不断向外侧拓展,有效增大了气泡夹带的横向体积,对长椭圆形变水滴撞击深水液池的大型气泡夹带起到了至关重要的作用.

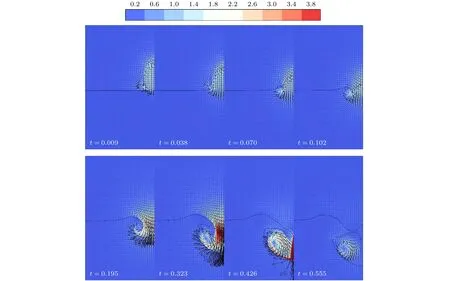
图8 不同时间节点下长椭圆形变水滴撞击液池速度矢量场 (Fr=112.5,We=145,Re=1740,Vi=6 m/s,AR=1.33)Fig.8.Velocity field of a prolate water droplet impacting into a water pool at selected times (Fr=112.5,We=145,Re=1740,Vi=6 m/s,AR=1.33).

3.3 涡环的运动过程

图9 自由表面下涡环的最大涡量随时间变化 (Fr=112.5,We=145,Re=1740,Vi=6 m/s)Fig.9.Vorticity maximum of the vortex ring generated under the free surface with time under different cases (Fr=112.5,We=145,Re=1740,Vi=6 m/s).

图10 自由表面下涡环的最大涡量位置随时间变化(Fr=112.5,We=145,Re=1740,Vi=6 m/s)Fig.10.Vorticity maximum location of the vortex ring generated under the free surface with time under different cases(Fr=112.5,We=145,Re=1740,Vi=6 m/s).

为了进一步研究水滴撞击深水液池时颈部生成的涡环随时间的运动及演变过程,选取撞击速度Vi=6 m/s下的5个工况对自由表面下生成涡环的最大涡量处随时间的运动过程进行详细地定量分析.图9和图10分别为自由表面下涡环的最大涡量及其生成位置随时间的变化关系.图9和图10中圆圈十字叉符号示意大型气泡夹带发生的节点.由图9易得,在不同形状水滴撞击深水液池的初期阶段,AR越小,液滴形状越接近扁椭圆形,则撞击初始水滴与液池颈部产生的涡环强度就越大.这种现象产生的原因来自于水滴撞击液池时颈部射流的曲率变化.在较扁的水滴与水池发生撞击时,水滴与液池接触的颈部会产生极细的射流,且水滴越扁,射流曲率越大,射流尖端越容易发生断裂.当接触颈部曲率增大时,尖锐的界面会带动水流,生成较强的涡量,使得涡环的强度大大增加.随着时间推移,各工况下的涡环强度都逐渐降低.由图9可见,在AR较大的长椭圆工况,涡环中心强度降低的速度较慢,而在AR较小的扁椭圆工况,涡环中心强度降低速度较快.较早的中心涡旋强度下降可能是由于水滴与深水液池之间的入水角度较大,涡环距离自由表面太近,涡旋与自由界面的相互作用提前开始,并被毛细波运动不断消耗而导致的,界面的早期拉动破坏了涡流的强度.对于涡旋深入液池中的长椭圆形变水滴,涡流强度不会受到早期界面拉力的破坏,因此涡旋强度下降相对较慢.

图10示意了涡环在深水液池中的运动和穿透过程.由图10可得,在水滴与液池接触颈部隆起射流的带动下,5种工况均表现出先上升后下降的大体趋势.不同的是,在AR=1.33的长椭圆形变水滴工况中,涡环下降后在强烈拉动自由界面形成滚动射流并一起移动时,先沿径向向外快速移动,随后向上偏转,并在相反方向重复了上述过程.这是由于滚动射流在内部涡环拉动及外部空腔气体涡流共同作用下产生摆动现象.在第二个偏转过程结束后,滚动射流在空腔中心碰撞,发生气泡夹带.对于AR ＜ 1的扁椭圆形变水滴而言,涡环在空间上长期跟随颈部射流,并一直附着于自由液面以下,未发生穿透效应.这也解释了扁椭圆形变水滴撞击时涡环强度下降较快的现象.

图11和图12分别为自由表面下涡环的最大涡量横向及垂向生成位置随时间的变化关系.图11和图12中圆圈十字叉符号示意大型气泡夹带发生的位置.由图11可得,水滴在撞击深水液池后,涡环的横向位置在前期基本跟随颈部射流的运动,表现出t=0.5之前的凸起.在AR=1.33的长椭圆形变工况中,涡环在滚动射流裹挟下,向射流尖端运动,因而横向长度减小,曲线呈下降态势,随后滚动射流汇合碰撞,涡环逐渐向外运动并消失.在其余工况中,颈部射流并没有发展成朝向空腔中心线运动的滚动射流,而是随着自由表面逐渐平复,因此涡环向空腔中心的方向运动,并随着自由面曲率的缓和逐渐消失.

图11 自由表面下涡环的最大涡量横向位置随时间变化(Fr=112.5,We=145,Re=1740,Vi=6 m/s)Fig.11.Lateral position of the vorticity maximum in the vortex ring generated under the free surface with time under different cases (Fr=112.5,We=145,Re=1740,Vi=6 m/s).

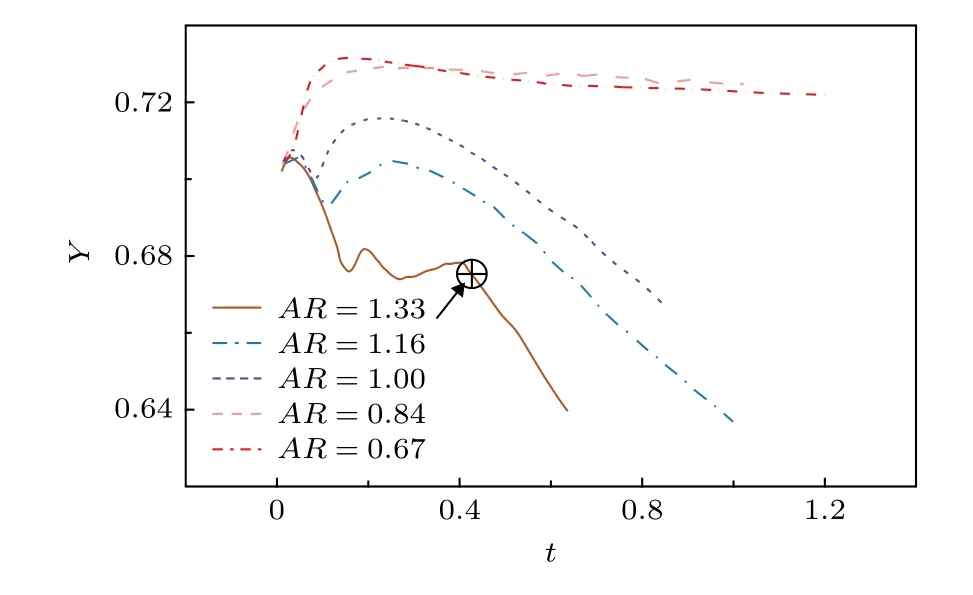
图12 自由表面下涡环的最大涡量垂向位置随时间变化(Fr=112.5,We=145,Re=1740,Vi=6 m/s)Fig.12.Vertical position of the vorticity maximum in the vortex ring generated under the free surface with time under different cases (Fr=112.5,We=145,Re=1740,Vi=6 m/s).

从图12中可得,扁椭圆形变水滴工况在跟随颈部射流上升后下降趋势十分缓慢,垂向位置基本紧贴自由表面,未能与水池发生穿透效应.而在AR=1.33的长椭圆形变工况中,由于颈部射流卷曲剧烈,发展成为滚动射流,所以涡环未能脱离射流,而是在射流内部随射流摆动而运动.在大型气泡夹带发生后,滚动射流互相碰撞,较大的动能将涡环向外推出,并向液池下方运动.综上所述,在垂直方向上,长椭圆形变水滴能够较早地与自由界面分离,以维持自身的涡量,而扁椭圆形变水滴一直跟随自由表面运动,因而涡量耗散较快.

4 结 论

采用基于自适应网格、不可压缩Navier-Stokes方程和VOF方法的开源程序Gerris对椭圆形变下微小水滴以不同速度撞击深水液池后的运动过程、气泡夹带以及涡环的发展进行了数值模拟,并详细研究了不同撞击速度和水滴形变对撞击后空腔变形坍缩过程、毛细波运动以及气泡截留的影响,主要得到以下结论.

1)在较低撞击速度下(Fr=75,We=64.4,Re=1160,Vi=4 m/s),不同形变的水滴并未引起显著的气泡夹带现象与空腔形态改变,扁圆形水滴对空腔底部涡量强度的作用小于其余两种水滴形变,在空腔边缘处的影响范围更宽.长椭圆形水滴则相反,对空腔底部运动的驱动作用显著强于其余正圆形及扁椭圆水滴形变.而在较高撞击速度下(Fr=112.5,We=145,Re=1740,Vi=6 m/s),AR=1.33下的长椭圆形变水滴与液池发生完全聚合现象,并产生大型气泡夹带,而在除正圆形水滴(AR=1)外的其余工况中,空腔形状由U形向V形转变,在液滴部分聚合生成细长中心射流并产生小型气泡截留.

2)大型气泡截留过程主要由水滴撞击深水液池时颈部自由表面下产生的涡环控制,涡环拉动自由界面之前,在液池中垂向移动较深,穿透性强,其后裹挟空腔上部界面形成滚动射流,最终射流接触合并以夹带大型气泡.在长椭圆形水滴撞击液面初期,毛细波运动一直跟随涡环,对空腔形态的塑造和滚动射流的产生起到了一定作用.在气泡截留后期,空腔内的气体涡旋推动空腔侧壁不断向外侧拓展,有效增大了气泡夹带的横向体积,对大型气泡夹带起到了至关重要的作用.

3)在撞击初期阶段,液滴形状越扁,颈部射流越大,撞击初始水滴与液池颈部产生的射流曲率越大,生成涡环强度就越大.但由于扁圆形水滴生成涡环紧贴自由面,界面的早期拉动破坏了涡流的强度,使得其中心涡旋强度下降较快.对于其他形变的工况而言,颈部射流的卷曲使得涡环在下降后在液池中呈抛物线式上下运动.发生大型气泡夹带时,涡环随滚动射流一起移动,先沿径向向外快速移动,随后向上偏转,并在相反方向重复了上述过程.这是由于滚动射流在内部涡环拉动及外部空腔气旋共同作用下产生摆动现象导致的.