基础实验题B：滤波电路的研究

惠王伟,钱 钧，牛紫平，王 槿， 于 健，陈 平，姚江宏，孔勇发

(南开大学 a.物理科学学院；b.基础物理国家级实验教学示范中心，天津 300071)

第5届全国大学生物理实验竞赛基础实验题B的题目为“滤波电路的研究”. 试题的第1题和第3题为常规实验，实验内容分别为一阶RC滤波电路和RLC串联谐振电路[1-2]，这部分主要考察考生的基础知识和实验操作能力. 试题的第2题和第4题是在常规实验的基础上的延伸，实验内容分别为二阶RC滤波电路[2-3]和电学黑盒子，这一部分主要考察考生的观察能力、现象分析能力和解决问题的能力.

1 原理背景

滤波电路可以允许一定频率范围内的信号成分正常通过，而阻止或者抑制另一部分频率成分通过. 按照所通过信号的频段可以分为低通、高通、带通和带阻几种类型的滤波电路[4].

在RLC交流电路中，电容元件和电感元件的阻抗与输入信号频率有关，电容元件的阻抗与频率成反比，电感元件的阻抗与频率成正比. 以电路中的1个元件上的电压作为输出电压，在总的输入电压不变的情况下，输出电压会随输入信号频率的变化而变化，这就形成了滤波电路. 大学物理实验中利用RC，RL稳态电路和RLC谐振电路可以实现不同类型的滤波电路[1，4].

2 实验器材

数字示波器，信号发生器，示波器和信号发生器的使用说明，电学九孔板，电阻4个，电感1个，电容3个，黑盒子(内含1个电感,1个电容，2个电阻),导线若干.

3 实验任务

3.1 一阶RC滤波电路(第1题)

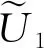
1)测量该电路的幅频特性曲线，并根据幅频特性曲线，按照频率通带范围，判断该电路属于什么类型的滤波电路.

2)计算当信号源频率f=800 Hz时，传递函数的模和幅角测量值与理论值的相对误差，给出幅角的测量过程.

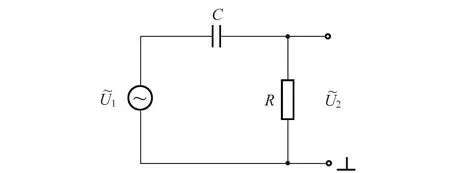
图1 一阶RC滤波电路

3.2 二阶RC滤波电路(第2题)

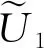
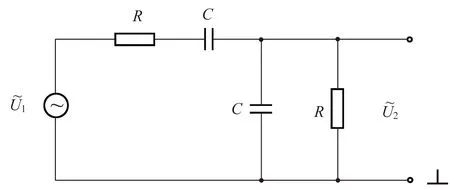
图2 二阶RC滤波电路

1)测量该电路的幅频特性曲线,并且根据幅频特性曲线，按照频率通带范围，判断该电路属于什么类型的滤波电路. 在幅频特性曲线中，找出|K|的最大值和其对应的频率.

2)计算当信号源频率f=3 kHz时，传递函数模|K|的测量值与理论值的相对误差. (保留2位有效数字)

3.3 串联谐振电路(第3题)

RLC串联谐振电路是常用的滤波电路(带通滤波电路). 本题可利用的元件为L1=0.04 H,C1=207.0 nF,C2=31.5nF,C3=43.0 nF,RL=51 Ω. 从上述元件中选取合适的元件搭建谐振频率f0=1.5 kHz的RLC串联谐振电路.

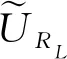
2)设置信号源输出峰峰值Vpp=5 V的正弦信号，当频率分别为500,1 500,2 500 Hz时,测量输入电压与输出电压，并且计算这3个频率下的|K|.

3)计算L1的串联损耗电阻rL，计算谐振电路的品质因数Q值.

3.4 电学黑盒子(第4题)

利用RLC电路可以搭建滤波和选频电路，同样利用RLC电路的输出特性可以判断电路元件的类别并计算元件参量.

电路黑盒子中电路连接如图3所示. 其中4个元件X1～X4中有2个电阻、1个电容和1个电感. 连接判断电路时，需要串联电阻R1=200 Ω，防止电路短路，且本题中信号源输出信号的峰峰值Vpp≤5 V，频率f<10 kHz.

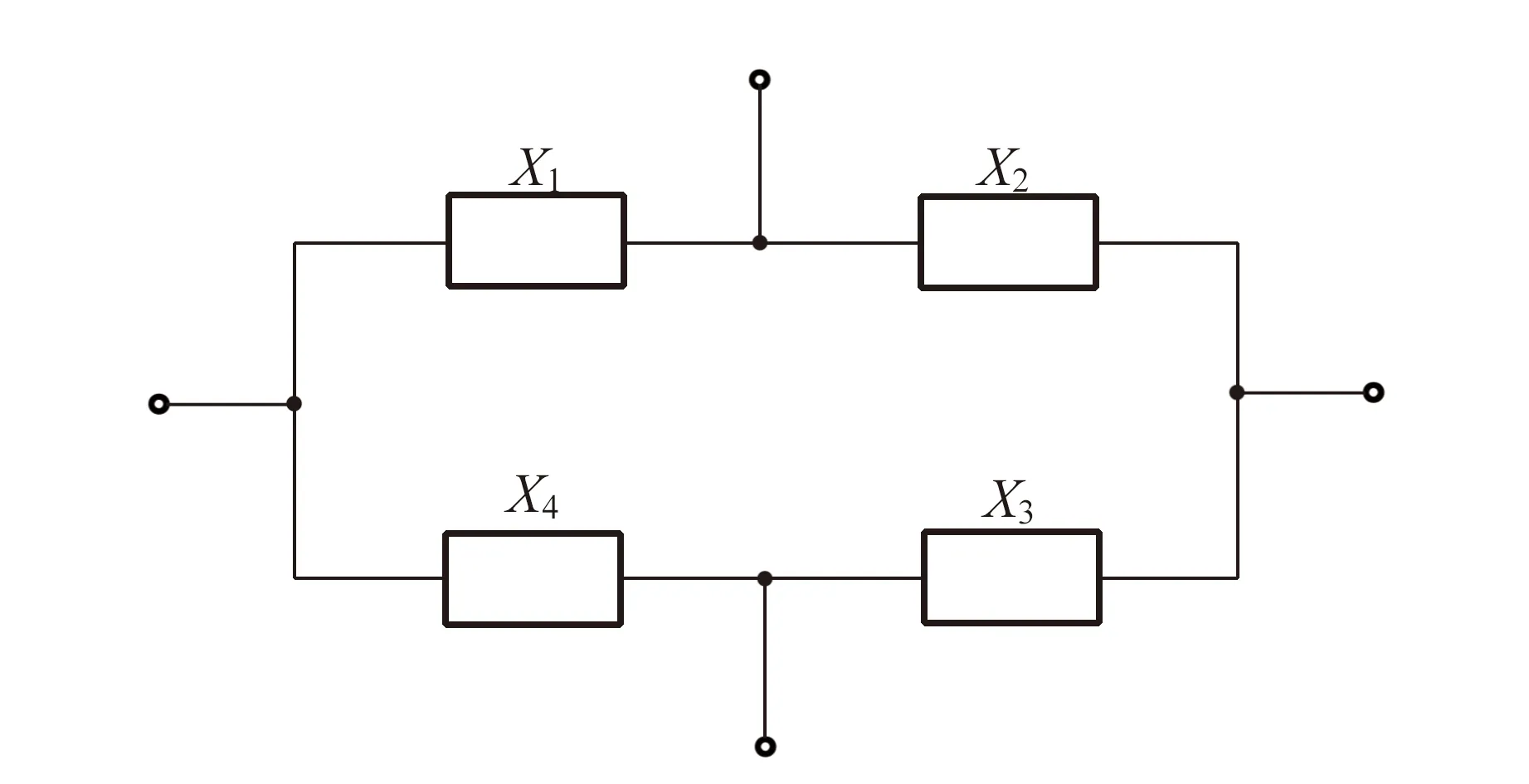
图3 黑盒子示意图

1)利用信号源、示波器和R1，判断X1～X4分别为何元件，并写出判断依据.

2)测量并计算元件参量(包括电阻值、电容值、电感值及电感串联损耗电阻值)，写出实验方法和计算过程.

4 试题解答

4.1 一阶RC滤波电路

1)按照图1搭建电路，测量电路传递函数的模|K|与频率关系，记录数据，该电路的幅频特性曲线如图4所示. 通过分析图4可知该电路是高通滤波电路.

2)根据交流电路知识可知电路传递函数的模|K|和幅角φ的表达式为

(1)

(2)

根据式(1)和式(2)可以计算出f=800 Hz时，传递函数的模和幅角的理论值. 传递函数的模的测量值可以直接从图4中获得，幅角的测量值通过测量输出和输入信号的相位差获得. 此处考察了学生如何测量2个信号的相位差的基本操作. 传递函数的模和幅角的相对偏差参考值分别为1.1%和5.6%.

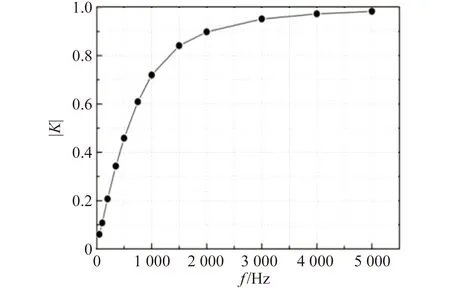
图4 一阶RC滤波电路的幅频特性曲线

4.2 二阶RC滤波电路

1)按照图2搭建电路，测量电路传递函数的模|K|与频率的关系，记录数据，该电路的幅频特性曲线如图5所示. 通过分析图5可知该电路是带通滤波电路，|K|值最大为0.33,对应的频率为1 000 Hz.

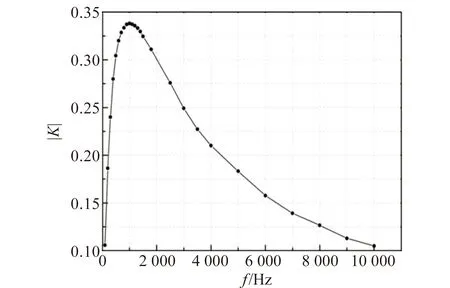
图5 二阶RC滤波电路的幅频特性曲线

2)利用交流电路的基尔霍夫定律可以得到该滤波电路的传递函数为

(3)

通过式(3)可以计算出f=3 kHz时传递函数的模，其测量值可以通过图5获得，相对偏差参考值为0.24%.

4.3 串联谐振电路

1)在谐振频率为1 500 Hz时，通过谐振条件

可以计算出所需要的电容为C=281.5 nF，所以需要将C1,C2和C3并联，电路如图6所示.

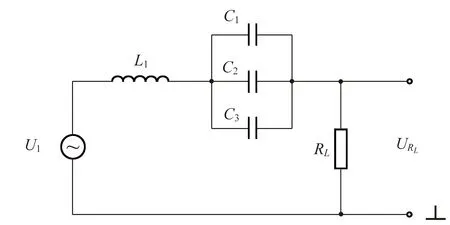
图6 串联谐振电路

2)设置信号Vpp=5 V，记录频率为500，1 500，2 500 Hz时，输入和输出信号的幅值，计算相应的|K|分别为0.054,0.555,0.126.

3)当电路处于谐振状态时，测得电路传递函数的模|K|=0.555,由谐振电路特性可知

4.4 电学黑盒子

1)黑盒子中有电阻、电容和电感，首先可以将对角的2个接线柱短接，简化电路，形成2个元件并联的情况，再将2个并联的元件与R1串联，与信号源组成回路. 以R1上的电压作为输出电压，利用示波器观察输入电压和输出电压的变化. 由RLC滤波电路特性可知，当电路为高通滤波电路时，2个并联的元件中有一个是电容，另一个是电阻或者电容；当电路为低通滤波电路时，2个并联的元件中有一个是电感，另一个是电阻或者电感；当电路为带通滤波电路时，2个并联的元件中有一个是电容，另一个电感. 通过判断可知X1是电容，X2是电阻，X3是电感，X4是电阻. 本题的判断方法有很多种，不一一介绍.

2)按照1)中的方法连接电路，首先将电容和电阻并联接入电路，设置信号源输出直流信号，这时电容相当于断路，通过电阻的分压可以测量出电阻值，然后设置信号源输出一定频率的正弦波，测量输入和输出信号的大小，可以计算出电容值. 然后将电感和电阻并联接入电路，同样设置信号源输出直流信号，这时并联的2个元件相当于电感的串联损耗电阻和电阻并联，通过电阻的分压可以计算出电感串联损耗电阻值，然后设置信号源输出一定频率的正弦波，测量输入和输出信号的大小，可以计算出电感值. 通过测量可得2个电阻值都为1 000 Ω，电感值为10 mH，电感串联损耗电阻值为51 Ω，电容值为1 μF.

5 考试结果和评析

本次竞赛中共有56位考生参加了基础实验题B的考试，图7是总分的分布情况. 通过图7可以看出，考生的总分分布基本满足高斯分布，区分度高.

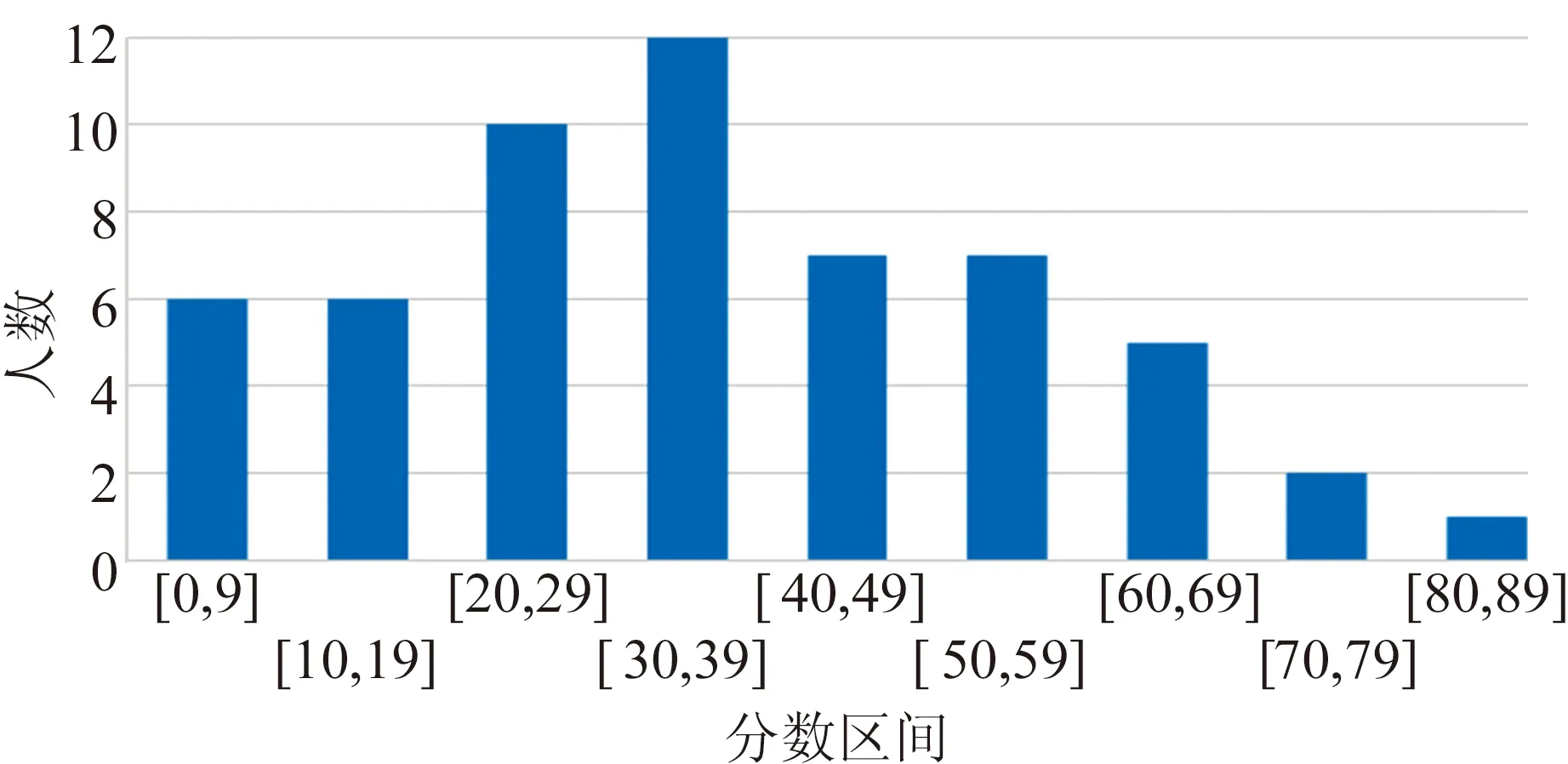
图7 总分分布图

图8是各个小题的得分情况.

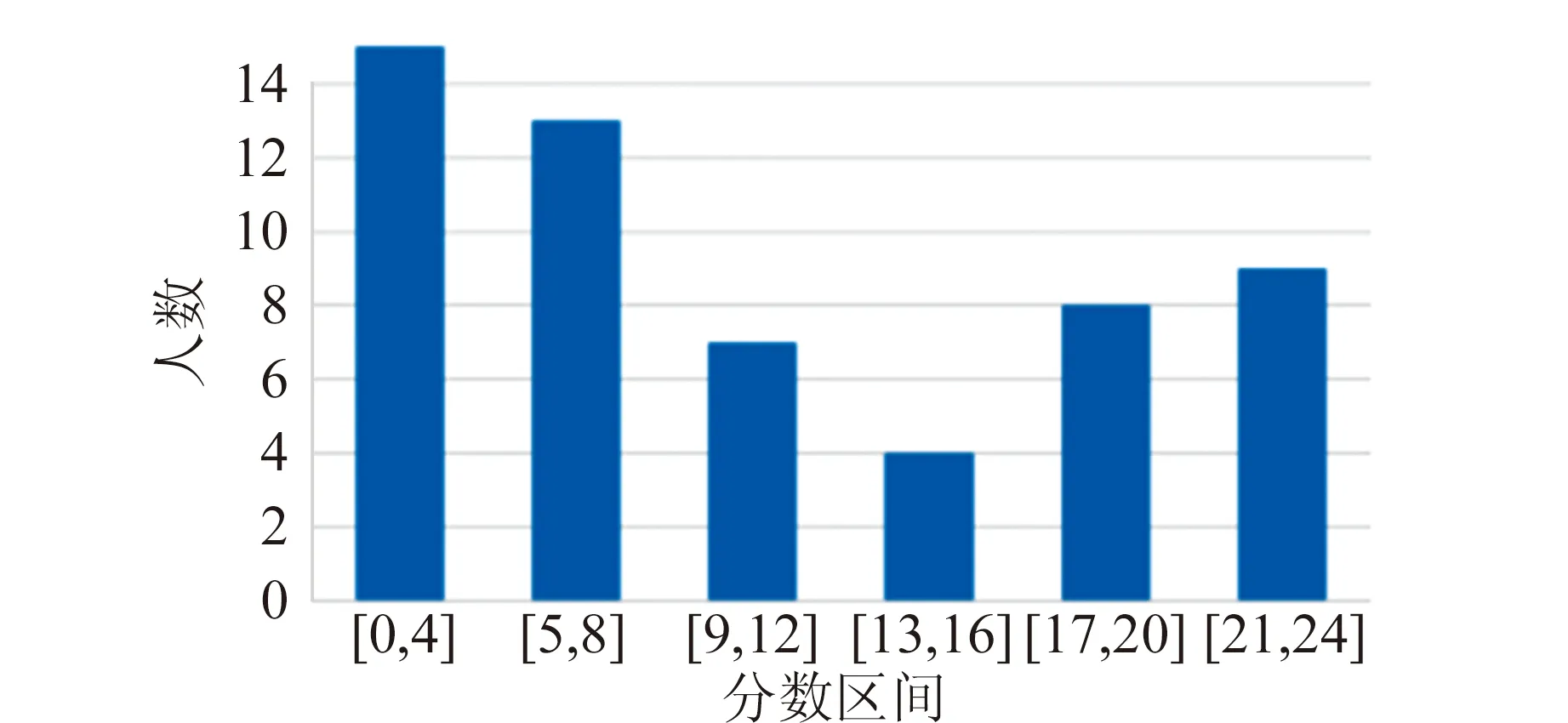
(a)第1题

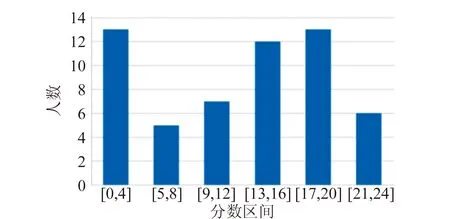
(b)第2题

(c)第3题

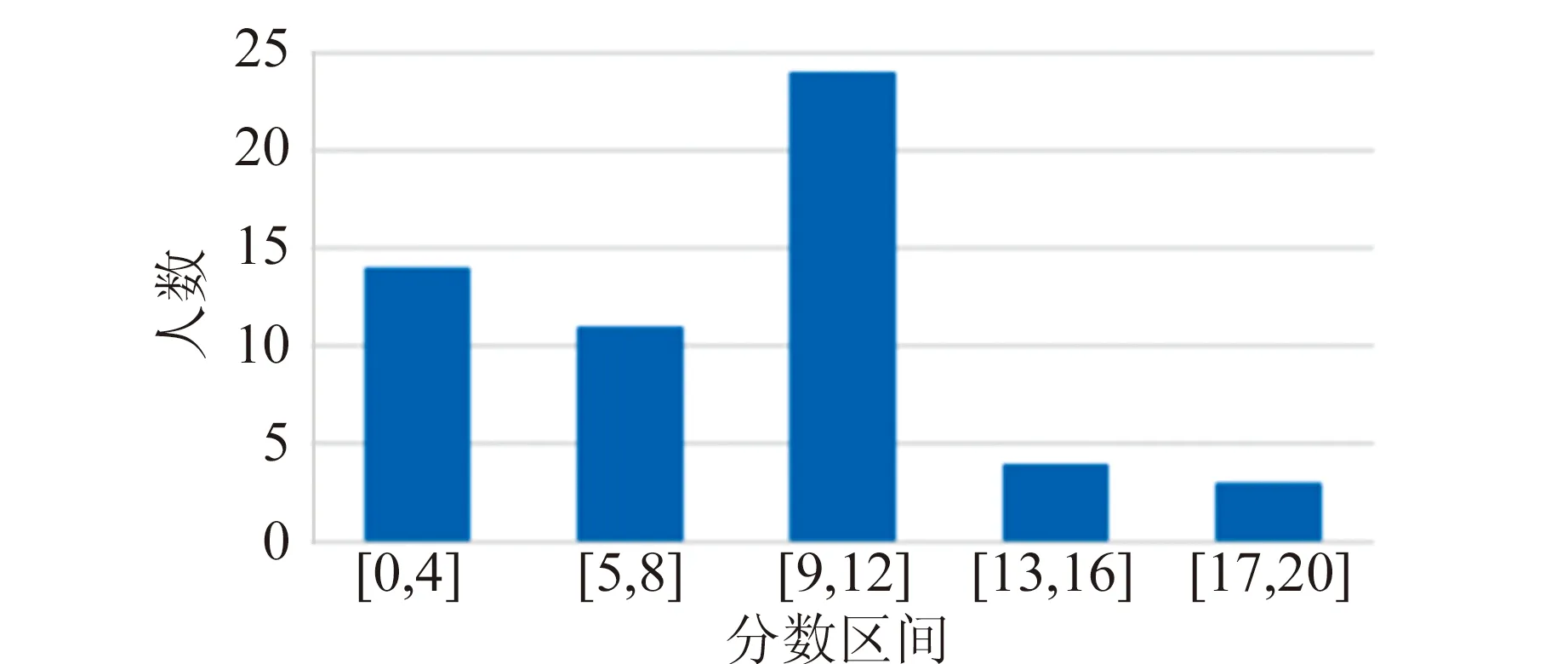
(d)第4题图8 各小题得分分布图

第1题总分24分，平均得分10.7分，2人满分，2人0分. 本题主要考察一阶RC滤波电路相关实验内容. 大部分考生可以根据题目要求搭建电路，完成数据测量，并画出幅频特性曲线，但也有很多考生因为数据测量点取值范围小，数据点少，作图不规范，数据误差大等原因造成失分. 还有部分考生因为交流电路基础知识掌握不牢，没有推出传递函数的表达式. 本题主要是RC稳态电路的基础实验内容. 从成绩分布图看出，呈现U型分布，得0～8分28人，而得17分以上17人，有两极化的倾向. 说明部分考生在对基础实验、基本测量操作以及数据作图规范的掌握上，还比较欠缺. 而在平时学习中掌握得比较好的考生，基本能够得到较高分数.

第2题总分26分，平均得分12.0分，最高分24分，5人得0分. 本题是在第1题基础上的延伸，主要考察二阶滤波电路相关内容. 大部分考生可以完成电路搭建和数据测量，并判断出电路类型. 同样由于数据误差较大和作图不规范等原因造成了失分. 排除少数0～4分区段的考生，本题得分分布基本满足高斯分布，区分度较好.

第3题总分22分，平均得分4.8分，2人满分，有近一半的考生得0分. 本题考查的是RLC串联谐振电路，大部分内容属于常规实验. 本题得分较低的主要原因是时间不足和实验方案错误. 很多考生对谐振电路相关知识掌握不牢，无法推算出所需元件参量，导致实验方案设计错误，也有部分考生实验误差较大，超出规定范围，造成失分.

第4题总分28分，平均得分8.6分，最高分20分，9人得0分. 本题主要考察考生利用滤波电路相关知识进行电学黑盒子的元件判断和参量测量. 大部分考生可以判断出4个元件的类型，但有些考生没有给出判断依据造成失分. 在元件参量测量方面，也有很多考生测量出了2个电阻的阻值，但只有少数几人测量出电容值和电感值. 本题可以充分反映出考生运用所掌握的知识解决实际问题的能力.

本试题在电学知识掌握程度、基本仪器使用能力、实验操作能力、数据处理能力和利用所掌握的知识解决实际问题的能力方面对考生进行了全面的考察,也反映出了很多考生实验能力不足等问题. 试题的相关实验装置简单，内容丰富，可以作为大学物理综合性实验，以丰富电磁学实验的内容.