部分填充水平旋转圆柱筒内涂层流动的实验研究

乔宇杰，张钰翔，周润中，唐明君

(四川师范大学 物理与电子工程学院,四川 成都 610101)

涂层流动是由于在与惯性、黏度、重力、表面张力等因素相关的外力作用下，在固体表面形成液体薄膜的一种流体流动[1]，在黏性涂层流体运动中，总是伴随着与内摩擦及传热有关的能量耗损过程，因此其运动不可避免地将和阻力、衰减、扩散等现象紧密地联系在一起[2-3]，在许多工业过程中发挥着重要作用，如造纸工业、滚筒涂布业、液体除气器、涡轮轴的冷却等[4]. 因此，许多研究小组都致力于对黏性液体在水平旋转圆柱筒内的流动行为进行研究[5-11]. 早期研究主要集中于对接近刚性旋转时的流体行为的研究[5-6]；后来，有些研究团队又对低转速下稳定的二维涂层流动行为进行实验探究和数值模拟[7-10]. S. T. Thoroddsen等对水平旋转圆柱筒中部分填充黏性流体的流体行为进行了实验研究，较为全面地描述了吊坠、鲨鱼齿、刚性旋转等实验现象[1]；A. E. Hosoi等研究了水平圆柱筒绕纵轴旋转时黏性流体自由表面的轴向不稳定性，导出了自由表面演化的简化模型方程，并对此方程进行了数值求解[7]；T. B. Benjamin等对高黏性液体部分填充时，以恒定角速度绕水平轴旋转的圆柱筒内液体可能发生的各种稳态和非稳态运动进行了研究[11].

本文采用自主研制的实验装置对水平旋转圆柱筒内部分填充黏性液体的流体行为进行了较为系统的实验研究. 研究内容包括在不同参量条件下，水平圆柱筒中的黏性液体从静止水池过渡到吊坠、吊坠消失、正弦波、鲨鱼齿波、波形晃动不稳、边缘流和刚性旋转等各种丰富的实验现象及动力学行为，并对出现这些实验现象做了初步的定性解释及定量研究.

1 理论基础

圆柱筒旋转时，由于黏性力的作用，流体会随着圆柱筒内壁一起运动，当运动到圆柱筒的侧壁上时，重力的作用增强，流体会沿侧壁向下运动. 在黏性力、重力、表面张力和惯性力的共同作用下，流体的自由表面会表现出不稳定性，因此将出现各种不寻常的实验现象.

假设黏性流体在水平圆筒中，其温度与体积不随时间的改变而改变，根据S T Thoroddsen的描述可知[1]：实验中涉及的物理量有：圆筒的半径R与长度l、黏性流体的体积Vf、流体密度ρ、流体动力黏度μ、流体表面张力系数σ、圆柱筒的转速ω及重力加速度g，流体在圆柱筒中的行为可以用流体的自由表面到圆柱筒内壁的高度h来描述. 根据量纲分析，选取流体黏度、表面张力系数、圆柱筒的半径以及重力加速度为独立量纲. 根据π定理，可以得到以下5个无量纲参量[1]：

(1)

2 实验方法

2.1 实验器材

有机玻璃圆柱筒(长40 cm，内直径8 cm，外直径9 cm)，可调转速电机，同步皮带，轴承(内径9 cm)，RC43数显转速表，甘油，刚果红染剂.

2.2 实验装置

如图1所示，圆柱筒两端分别嵌套一轴承，用台虎钳夹持轴承外圈可固定实验装置. 圆柱筒右端粘连1圈同步皮带，用环形同步皮带与电机的皮带轮相连，通过皮带驱动可使圆柱筒获得稳定的转速，调节电机的转速控制旋钮可以改变电机转速. 圆柱筒转速的测量是由同侧的霍尔传感器测转速装置完成，该装置由RC43数显转速表、霍尔传感器[12]、圆形磁铁(直径1 cm)和直流电源组成. 将RC43数显转速表、霍尔传感器和12 V直流电源相连接，磁铁粘连在圆柱筒右侧面，霍尔传感器放置在距离侧面约1 cm位置处，当圆柱筒转动时，磁铁就会经过传感器的探测位置，测量出圆柱筒的转速. 圆柱筒左端侧面圆心处有直径为6 mm的小孔，用于液体的填充与抽取. 填充液体为甘油与水的混合溶液，改变配比可得不同黏度的甘油水溶液，并使用刚果红染剂将液体染色，便于实验现象的观察.

(a)正视图 (b)俯视图图1 实验装置图

2.3 实验步骤

刘竹琴等利用落球法测定了不同体积分数下甘油的黏度，并根据实验结果给出了甘油的黏度与体积分数(甘油与水的体积比)的关系曲线及拟合方程[13]. 为避免温度对实验的影响[14]，控制实验室温度为23 ℃，测得甘油密度1 261.4 kg/m3，水的密度998.2 kg/m3，由文献[13]中实验所得的拟合方程，可知不同配比的甘油水溶液对应的黏度，同时本文使用FB326型表面张力系数测定仪对不同配比的甘油水溶液的表面张力系数进行测量，其结果如表1所示[15-16].

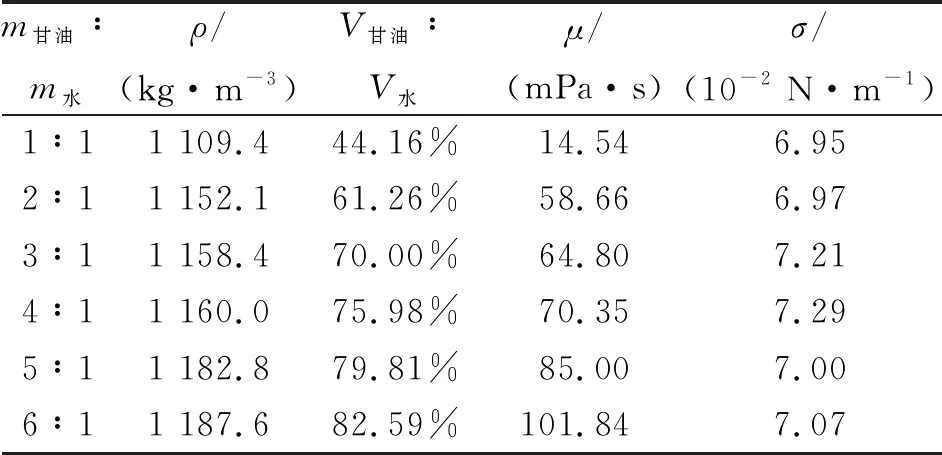
表1 甘油-水混合溶液参量

在圆柱筒中注入不同黏度和不同填充体积分数的黏性液体：根据甘油水溶液的密度、密度与体积的关系(m=ρVf)及圆柱筒的几何参量，可以计算出某填充体积分数时所需的溶液质量. 在实验中，采用固定参量法，首先固定液体黏度，改变圆柱筒转速与填充体积分数，然后固定填充体积分数，改变圆柱筒转速与黏度进行实验探究. 观察随着参量的改变，水平旋转圆柱筒内的涂层流动的变化情况.

3 实验结果

3.1 实验现象

如图2所示，在零转速下，液体静止，位于圆柱筒底部的静止水池. 当圆柱筒开始旋转，假设为顺时针旋转，液体将沿顺时针方向从底部水池后端中被带出，直至涂覆在整个圆柱的内表面，再回到水池的前端，在底部形成再循环区域[1].

随着转速的增加，从水池中拉出的水层变厚，当转速达某一值时，涂层变得不稳定，由于重力作用，将在上升一侧形成落波，落波开始是平行于轴的直线状，但随着转速的增大，它将分解成若干单独的近似抛物线形状的波，将其称作“吊坠”[如图3(a)][1]，在一定的速度范围内，该现象是不稳定的，即“吊坠”总是在不断地生成与消失，且具有随机性. 当转速继续增大，在某一很小的转速范围内，这种“随机吊坠”的现象消失，继而出现“固定吊坠”的现象[见图3(b)]，即“吊坠”孤立且稳定地出现在上升一侧的侧壁上，当角速度继续增大时，该现象消失，此后，即使继续增大转速，侧壁上都不会再出现“吊坠”.

图2 再循环区域示意图

转速从零开始缓慢增加时，在圆柱筒底部会形成再循环区域，随着转速的增大，该再循环区域的前端(即液体进入再循环区域的位置)也会出现某些不寻常的现象，其前端不再是平行于轴的直线状，而是会出现波状[见图3(c)]，这些波的振幅会随着角速度的增大而增大，当转速增加到一定值时，该现象会变得不稳定[见图3(e)]，波形会出现晃动，并随着转速的增大而晃动得越剧烈，在更高的转速下，液体均匀地包覆着圆柱体的内壁[见图3(h)]，并与之一起刚性旋转.

以黏度为64.80 mPa·s、填充分数(液体体积与圆柱筒容积之比)6.5%为例，讨论改变圆柱筒转速时出现的各种实验现象. 当转速为93 r/min时，在上升一侧(见图2)的侧壁上出现 “吊坠”，此时大部分的液体在底部的再循环区域[见图3(a)]. 此时是从正面拍摄，左端往右端看，圆柱筒顺时针转动，即后侧为液体上升一侧，所以拍摄的现象出现在后侧壁上. 当转速增大为96 r/min时，出现“固定吊坠”，即吊坠稳定的出现在某位置，直至转速增加才消失[见图3(b)]. 当转速增大为157 r/min时，在再循环区域的前端会形成正弦形状的波纹[见图3(c)]，且随着转速的增大，波长会变大，波数会减少. 此时是从上面拍摄，左端往右端看，圆柱筒逆时针转动，拍摄的现象出现在圆柱体的底部，出现波纹的一端，即再循环区域的前端. 当转速增大为182 r/min时，前端的正弦波形变得尖锐，称之为“鲨鱼齿”[见图3(d)][17]，即正弦波出现在157～182 r/min转速范围内. 当转速继续增大到235 r/min时[见图3(e)]，前端的鲨鱼齿波形开始左右晃动，不再稳定，且随着转速的增大晃动愈剧烈，即稳定的鲨鱼齿出现在182～235 r/min转速范围内. 随着转速的增大，波形越来越不稳定，直到转速为278 r/min时，开始有部分区域(指一定宽度的纵向圆柱面)的圆柱筒被均匀涂覆，看起来就像是前端的波状的液体从后端被拉上去，涂覆在圆柱筒上，此即进入“边缘流模式”[见图3(f)]. 随着转速的继续增大，圆柱筒越来越多的区域被均匀涂覆，在圆柱筒内壁上会出现环状图案[见图3(g)]，直到转速到达356 r/min时，侧壁全部被均匀涂覆[见图3(h)]， 此时筒内的液体与圆柱筒不再发生相对流动，称为“刚性旋转”. 转速大于356 r/min后，液体将一直保持刚性旋转.

(a)随机吊坠

(b)固定吊坠

(c)正弦波形

(d)鲨鱼齿波形

(f)边缘流模式1

(g)边缘流模式2

(h)刚性旋转图3 不同转速下圆柱筒内壁图案

3.2 实验数据处理

选择质量比为2∶1、黏度μ=58.66 mPa·s的甘油水溶液，改变填充体积分数η，以0.5%为梯度，从 3.5%增加到9.0%，如表2所示，其中m为填充质量，Vf为填充体积，η为填充体积分数，h0为平均液膜厚度. 各种实验现象的临界转速将发生变化，如图4所示，得到了改变体积分数和临界转速的实验相图. 随着填充体积分数的增加，出现吊坠、吊坠消失、正弦波、鲨鱼齿波、边缘流和刚性旋转等各种实验现象所对应的临界转速.

从图4中可以看出，在正弦波与晃动不稳定过渡区域之前，随着体积分数的增大，出现吊坠和吊坠消失的临界转速略有减小，即在水平圆柱筒低速转动时，随着填充体积分数的改变，临界转速的变化不够敏感. 这表明在低速旋转时，在圆柱筒内加入的没有滑移的液体图层被拉上来出现图案时，液体自由表面保持节奏稳定的状态，表示阻力和表面张力有助于建立与重力的平衡，在这种情况下，旋转效应可以不予考虑[4]. 反之，出现正弦波、出现边缘流和刚性旋转的临界转速，随着填充体积分数的增大而明显升高. 刚性旋转临界转速的增大是因为液体越多，需要使其涂覆在圆筒内表面所需的离心力就越大[1].

表2 实验中各参量

图4 黏度为58.66 mPa·s时转速与体积分数的实验相图

对于鲨鱼齿现象，其流动区域为闭区域，也就是说，如果参量沿着这个区域以外的一条曲线变化，流体可能不会出现鲨鱼齿模式而直接从前端波形过度至边缘流模式区域. 由文献[1]可知，前端波形模式和鲨鱼齿模式都遵循相同的机理，它们的区别只是波形振幅的不同. 本文的实验结果与Hosoi A.E.等对鲨鱼齿的计算模拟结果一致[7].

当转速增大到一定程度时，流体都会与圆柱筒一起刚性旋转，且这个临界转速随填充体积分数的增大而增大. 这是因为刚性旋转模式是重力与黏性力、惯性力平衡的结果[1]. 当体积分数增大时，液体的重力显著增大，而黏性力的变化不明显，此时主要是惯性力与重力的平衡，而惯性力与转速呈正相关.

图5 临界雷诺数随填充体积分数的变化

选择不同黏度的甘油水溶液，固定每次实验时的填充体积分数η=6.5%，可以得到各种现象的临界转速随黏度增加时发生的变化，结果如图6所示.

图6中，横坐标为液体黏度，纵坐标为圆柱筒转速，不同黏度的液体的质量比m甘油:m水分别为表1中2∶1,3∶1,4∶1,5∶1,6∶1的甘油水溶液，即黏度大小分别为58.66,64.80,70.35,85.00,101.84 mPa·s. 实验测量了随着转速的改变，各种黏度的液体出现正弦波、鲨鱼齿波、边缘流和刚性旋转等实验现象的临界转速. 从图6中可以看出，随着液体黏度的增加，各种现象出现的临界转速都在减小. 从图6中可以发现，鲨鱼齿区域与边缘流模式区域之间的波形晃动不稳区域随着黏度的增大明显减小，说明在体积分数不变的情况下，液体的黏度越大，鲨鱼齿波形越稳定，所以波形晃动不稳出现的转速会范围减小. 而当黏度增大时，流体所受的黏性力显著增加而重力几乎不变，因此达到平衡时的惯性力就越小，出现刚性旋转的临界转速就越小.

图6 转速与黏度的实验相图

4 结束语

搭建了稳定的实验装置，测试了在不同参量条件下，水平圆柱筒中的黏性流体的动力学行为. 通过改变实验参量，发现各种明显的行为模式都有明确的参量区域. 按照非线性动力学的说法，即存在不同的吸引子，且每个吸引子有明确的吸引域[18]. 根据实验，得到了当液体黏度固定时，改变转筒转速与填充体积分数以及固定填充体积分数时，改变转筒转速与液体黏度，出现吊坠、吊坠消失、正弦波、鲨鱼齿波、边缘流和刚性旋转图案现象的实验相图，并给出定性解释，同时计算了吊坠、边缘流、刚性旋转的临界雷诺数随体积分数的变化关系，结果表明：吊坠的出现存在与填充体积分数无关的临界雷诺数，而边缘流与刚性旋转出现的临界雷诺数则与填充体积分数成线性正相关. 这对水平旋转圆柱筒内的黏性液体的流体动力学研究具有一定的参考价值.

致谢:四川师范大学物理实验中心为本课题提供的实验场地与资金支持；四川师范大学物理与电子工程学院王涛老师、段满益老师、张原维老师为本课题的指导和提出的宝贵建议，在此一并表示感谢！