基于单类支持向量机的冷水机组温度传感器故障检测

毛前军 梁致远 刘冬华 胡云鹏2 李冠男 方 曦

(1 武汉科技大学城市建设学院 武汉 430065； 2 武汉商学院 武汉 430056)

冷水机组作为空调系统的重要组成部分，在实际运行过程中，常因不同环境条件及运行模式的影响出现不同故障，造成能源浪费、用户投诉、设备过度损耗[1-2]等问题。故障检测和诊断(fault detection and diagnosis, FDD)方法作为确保冷水机组正常运行的重要方法，对空调系统高效运行及节能起至关重要的作用。值得注意的是，传感器测量数据的准确性及可靠性[3-4]对故障检测和诊断的效果有十分显著的影响。由于传感器故障导致的测量精确性下降可能造成系统控制策略不当，最终影响空调系统能耗及建筑服务成本[5-7]，因此有必要对冷水机组传感器故障的检测和诊断进行研究。

近年来，基于冷水机组运行数据的FDD研究已成为制冷空调领域内的一个热点课题。随着研究方法的不断发展和改进，支持向量数据描述(support vector data description, SVDD)及支持向量机(support vector machine, SVM)已被广泛应用于冷水机组FDD领域。Zhao Yang等[8]利用SVDD进行了冷水机组及传感器的故障检测工作，与主元分析方法(principal component analysis, PCA)相比，该方法具有更高的故障检测效率。Han Hua等[9]结合遗传算法(genetic algorithm, GA)设计了“一对一”多类SVM模型应用于冷水机组重要传感器的自动化FDD，在降低测试时间的同时取得了较优的诊断效果。Yan Ke等[10]针对冷水机组FDD提出了一种结合外生变量的自回归(auto-regressive modeling with exogeneous inputs, ARX)模型与SVM混合的方法，与传统方法相比获得了较高的预测准确率及较低的虚警率。

单类支持向量机(one-class support vector machine，OC-SVM)与SVDD类似[11]，同为基于SVM理论的单分类方法。该方法在冷水机组故障数据样本不足或难以获得故障数据样本时，能够依据机组运行的正常数据进行学习并得到一个决策边界用于检测机组是否发生故障。OC-SVM在处理高维度、非线性数据集的分类问题时[12]具有较好的效果，目前已在手写体识别[13]、卫星图像提取[14-15]、入侵检测[16]、信息追踪[17]等研究方向取得了不错的成果，而在冷水机组传感器故障检测领域中鲜有应用。因此，本文提出一种基于OC-SVM的检测方法，用于检测冷水机组温度传感器偏差故障。

1 OC-SVM分类原理

OC-SVM最先由B. Schölkopf等[18]提出，基本思想为通过训练正常数据样本，在特征空间中构造一个最优超平面以实现训练样本与原点距离的最大化，如图1所示。

图1 OC-SVM原理Fig.1 The principle of OC-SVM

对于正常样本数据集Χ=[x1,…,xN]T∈RN×L，为获取决策超平面f(x)=ωφ(x)-ρ=0，考虑求解优化问题：

(1)

(2)

式中：N为样本个数，υ∈(0,1)为正则化参数；ξi为xi(i=0,1,…,N)对应的松弛变量；ω和ρ为决定决策超平面的参数；φ为数据由原始非线性空间到特征空间的映射。

引入拉格朗日乘子αi≥0及βi≥0，求解拉格朗日方程：

(3)

对上述方程中的各变量求偏微分后可得该优化问题的对偶形式：

(4)

(5)

式中：α=[α1,…,αN]T，H为由Hij构成的核矩阵，Hij可表示为：

(6)

K(xi,xj)为核函数，采用如式(7)所示的RBF核函数，仅有一个参数σ需调节，该参数影响RBF核函数的宽幅。

(7)

通过求解上述二次规划问题，即可解出α，于是ω和ρ可由式(8)～式(9)分别算出：

(8)

(9)

由解出的ω和ρ即可求得特征空间中的决策超平面。

对于训练集Z=[z1,…,zM]T∈RM×L，建立了基于欧式距离的决策函数F(zk)(k=0,1,…,M)用于对测试样本zk进行分类：

(10)

通过计算测试样本zk的决策函数F(zk)来判断zk与决策超平面的位置关系。若F(zk)=+1时，zk落在决策超平面之内，被分类为正类，即判断为正常样本；若F(zk)=-1时，zk落在决策超平面之外，被分类为负类，即判断为故障样本。

2 故障检测流程

基于OC-SVM的温度传感器故障检测流程如图2所示，主要分为模型建立阶段和故障检测阶段。

模型建立阶段：1)建模前对训练集X0∈RN×L进行均值为0、标准差为1的标准化处理；2)在标准化后的训练集X∈RN×L上，依据十折交叉验证法，寻找模型优化参数(υopt,σopt)；3)基于寻得的优化参数建立OC-SVM模型用于故障检测。

故障检测阶段：1)在测试集Z0∈RM×L中引入单变量固定幅值的传感器故障偏差，使用与训练集标准化相同的映射规则处理测试集数据；2)通过已建立的OC-SVM模型处理标准化的测试集Z∈RM×L；3)依据所获得的被测数据决策函数F(zk)判断冷水机组运行状况。

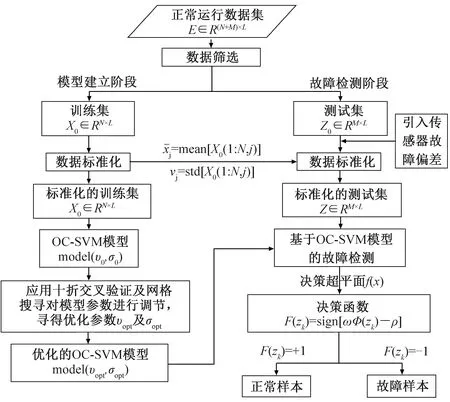
图2 基于OC-SVM的冷水机组温度传感器故障检测流程Fig.2 Flow chart of fault detection on temperature sensor in chiller based on OC-SVM

3 实验数据

3.1 数据与特征选取

选取两个工程实测数据集、两个实验数据集验证了基于OC-SVM的冷水机组温度传感器故障检测方法的有效性。

各数据集的基本特征如下：数据集Ⅰ为武汉市某电子厂7月份至9月份螺杆式冷水机组正常运行数据[19]。剔除记录不完整的数据样本后得到612组训练数据和456组测试数据；数据集Ⅱ为武汉市某高校地源热泵机组(夏季气候条件下，地源热泵机组持续产生冷水，向室内风机盘管提供冷量)7月份和8月份正常运行数据，该数据集包含460组训练数据以及253组测试数据；数据集Ⅲ及数据集Ⅳ均来自ASHARE RP-1043中离心式冷水机组正常运行数据[20]。

数据集Ⅲ的冷冻水供水的温度设定值分别为10.0、7.2、4.4 ℃，包含410组训练数据及410组测试数据；数据集Ⅳ的冷冻水供水的温度设定值为7.2 ℃，包括130组训练数据及130组测试数据。两组数据集冷却水供水温度在16.7～29.5 ℃阶跃运行。

根据能量守恒定律及测试参数相关性[21]，选择8个特征变量建立OC-SVM模型，即[Tchws，Tchwr，Qchw，Tcws，Tcwr，Qcw，P，Mref]，分别为冷冻水侧供水温度、冷冻水侧回水温度、冷冻水侧体积流量、冷却水侧供水温度、冷却水侧回水温度、冷却水侧体积流量、机组功率及控制系统反馈信号。由于机组类型的不同，选用数据集Ⅱ时，采用机组制冷量Qref及耗电量W来替代变量Qcw和Mref进行建模。选用数据集Ⅲ时，变量Mref代表阀门控制反馈信号；选用数据集Ⅳ时，变量Mref代表滑阀位置反馈信号。

3.2 模型参数优化

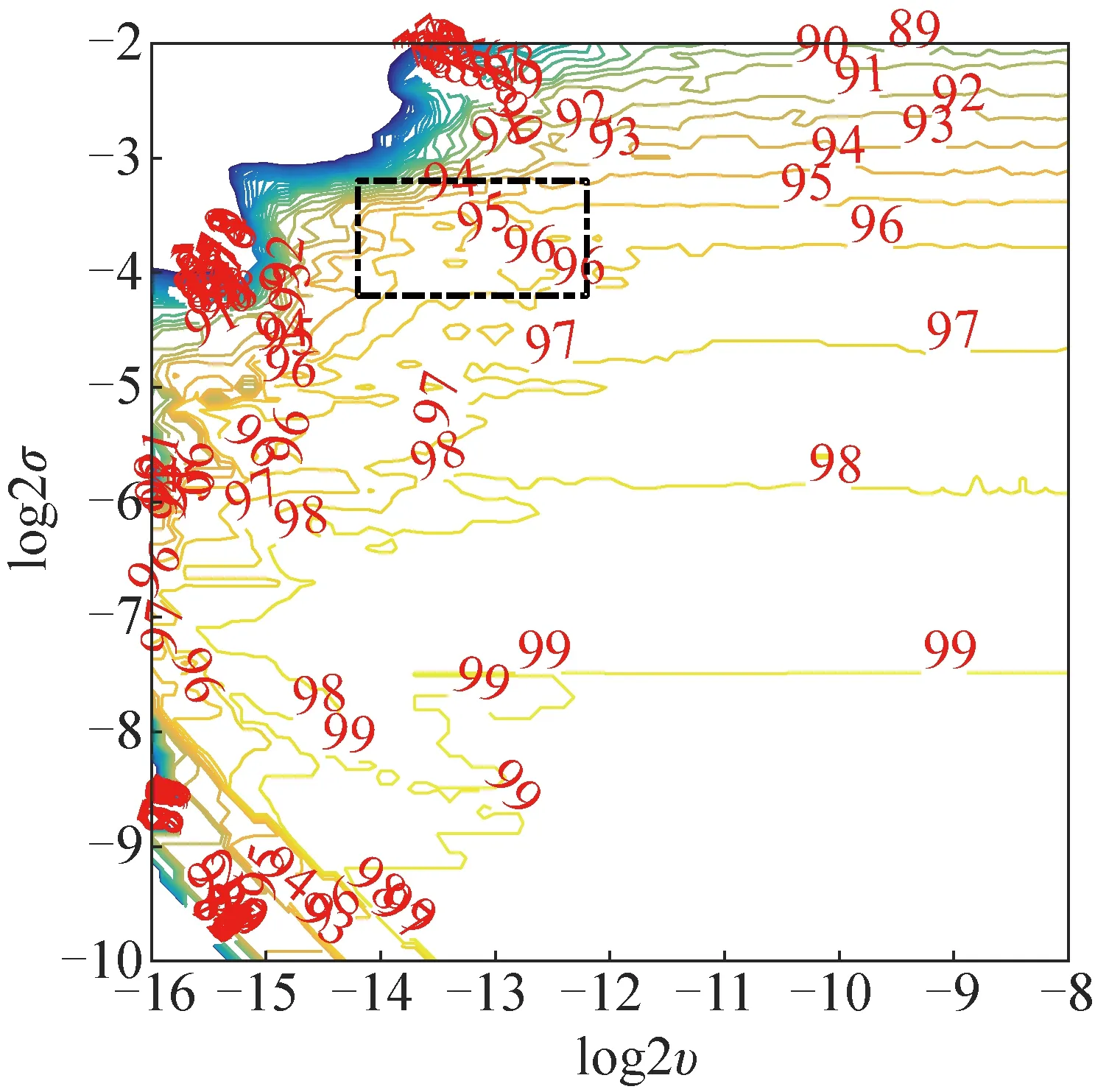
图3 十折交叉验证中优化参数精细搜索区域(数据集Ⅰ)Fig.3 Results of 10-fold cross validation using grid search method (dataset Ⅰ)

采用十折交叉验证法进行模型参数寻优，筛选出一组合理的优化参数建立模型，避免出现过拟合现象。文献[11, 22]表明，参数υ越小，模型拟合非线性的能力就越强，参数σ越大，支持向量个数越少，决策边界越松散。本实验中，十折交叉验证准确率控制在90%以上，选择υ较小、σ较大的区域为交叉验证中网格参数的精细搜索范围，于区域内得到一组基于训练集的优化参数(υopt,σopt)，根据该组参数建立OC-SVM模型。图3所示为黑色方框给出了选用数据集Ⅰ进行建模时，十折交叉验证法网格参数寻优的精细搜索范围。表1所示为数据集Ⅰ～Ⅳ的模型优化参数值，并给出了各训练集冷冻水供、回水的最大值、最小值、标准差。

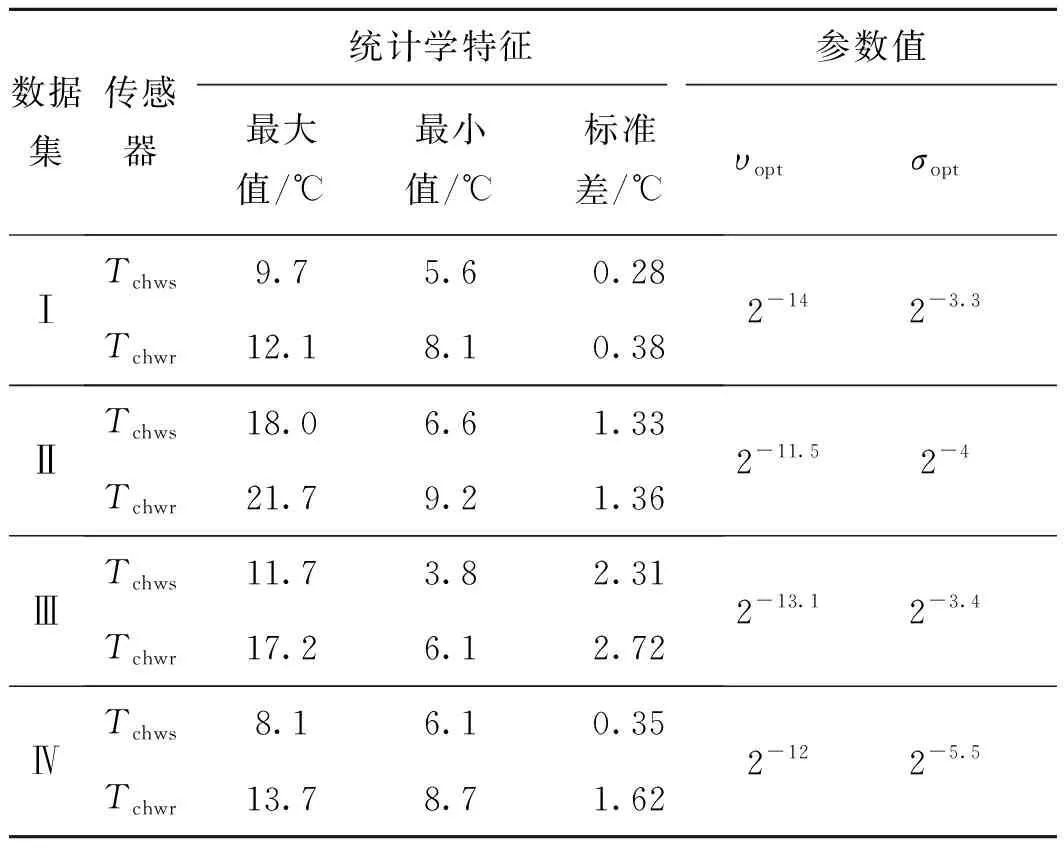
表1 训练集统计学特征与模型优化参数值Tab.1 Statistical characteristics of training sets and parameter values of model optimization

4 结果验证

对数据集Ⅰ～Ⅳ的Tchws及Tchwr分别引入幅值范围为-4～4 ℃、间隔1 ℃的传感器偏差故障。定义负类分类率为：测试集中被模型分为负类的样本个数与测试集样本总数的比值，数值上等于传感器偏差故障检测效率(测试集中被检测为故障样本的个数与测试集样本总数的比值)。

4.1 决策函数F(zk)

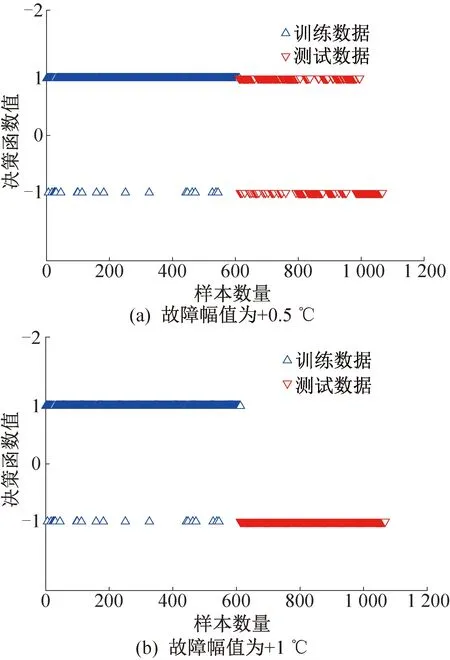
图4 Tchws传感器故障幅值为+0.5 ℃和+1 ℃时的决策函数值Fig.4 Decision function plots of Tchws sensor fault deviations at +0.5 ℃ and +1 ℃

以选用数据集Ⅰ为例进行基于OC-SVM方法的偏差故障检测。图4所示为Tchws传感器故障幅值为+0.5 ℃及+1 ℃时的决策函数值。其中训练集(样本数量1～612)中有588个样本的决策函数F(xi)取值为+1，即96%训练数据被分类为正常样本，训练集整体保持稳定。

由图4中测试数据(样本数量613～1 068)发现，故障偏差为+0.5 ℃时，456个测试样本中决策函数F(zk)取值为-1的样本只有215个，即负类分类率为47%；而当故障幅值增至+1 ℃时，测试集中456个样本的决策函数F(zk)取值全部为-1，负类分类率显著提升至100%。随着引入故障幅值的增大，测试样本越容易向决策超平面外移动，决策函数F(zk)取得-1的概率显著增加，即越容易被分类为负类样本。

4.2 检测结果及分析

表2所示为数据集Ⅰ～Ⅳ的Tchws和Tchwr在不同偏差故障幅值下的传感器故障检测效率，可以看出基于OC-SVM的方法能有效检测出Tchws及Tchwr传感器上的偏差故障。

1)数据集Ⅰ：当偏差故障幅值绝对值≥1 ℃时，Tchws和Tchwr传感器的故障检测效率均≥95%，大于1 ℃时达到100%，检测效果明显。

2)数据集Ⅱ：对比Tchws与Tchwr传感器在相同偏差故障幅值下的检测效率，发现两者具有十分接近的检测效果。而对比两者在负偏差与正偏差上的检测效率发现，基于OC-SVM的方法在负偏差上的故障检测能力要明显高于正偏差。在-4 ℃故障幅值下，Tchws和Tchwr传感器的检测效率均超过90%，检测效果较好；在+4 ℃故障幅值下，两者检测效率超过60%。

3)数据集Ⅲ：基于OC-SVM的方法在该数据集上的检测效率略低。在-4 ℃故障幅值下，Tchws和Tchwr传感器检测出了超过45%的故障数据；在+4 ℃故障幅值下，两者检测效率均超过50%。

4)数据集Ⅳ：数据集Ⅲ与数据集Ⅳ的主要区别在于后者的冷冻水供水设定温度保持在7.2 ℃，因此后者冷冻水供水的测量数据变化范围要明显小于前者。表2显示，Tchws传感器的偏差故障检测效率要优于Tchwr传感器。当Tchws传感器偏差故障幅值绝对值≥2 ℃时，检测效率均大于95%，检测效果显著，同时Tchwr传感器在-4 ℃故障幅值下的检测效率可以达到72%。

5 结论

本文提出了一种基于OC-SVM的冷水机组温度传感器故障检测方法，选取了4组不同的冷水机组数据，分别选择每个数据集中的8个变量建立了对应的OC-SVM故障检测模型。采用十折交叉验证法寻得模型优化参数，运用优化后的模型对传感器偏差故障进行了检测。通过对检测结果进行分析，验证了该方法的有效性，得到如下结论：

1)基于OC-SVM的方法对温度传感器偏差故障具有较好的检测能力。对于螺杆式冷水机组(数据集Ⅰ)的检测效果尤为明显，在冷冻水侧温度传感器偏差故障幅值绝对值≥1 ℃时，检测效率达到100%。4个数据集的检测结果显示，检测效率随故障幅值的增大而增大。对于不同温度传感器的不同程度偏差故障，其检测效率存在一定的差别。

2)OC-SVM模型十分依赖于训练集的数据质量，数据变化范围小、标准差小的训练集有助于学习到一个边界紧凑的OC-SVM分类模型，从而一定程度提高了模型检测能力。

3)基于OC-SVM的检测方法可应用于冷水机组故障检测中，但对不同数据集的检测效果并不一致。下一步将运用该方法进行不同类型冷水机组的传感器故障检测，与常见故障检测方法进行对比并分析其优缺点，研究不同类型数据对该方法检测效率的影响。同时考虑将该方法运用于在线冷水机组故障检测中，建立合适的距离监测量以便实现故障检测过程可视化。

符号说明

υ——正则化参数

ξi——松弛向量

ω、ρ——决策超平面参数

N——训练集样本个数

M——测试集样本个数

L——样本数据维度

φ——非线性映射

αi、βi——拉格朗日乘子

K(xi,xj)——核函数

σ——RBF核函数参数

F(xi)——训练集样本决策函数值

F(zk)——测试集样本决策函数值

Tchws——冷冻水侧供水温度，℃

Tchwr——冷冻水侧回水温度，℃

Qchw——冷冻水侧体积流量，m3/h

Tcws——冷却水侧供水温度，℃

Tcwr——冷却水侧回水温度，℃

Qcw——冷却水侧体积流量，m3/h

P——机组功率，kW

Mref——系统控制反馈信号

Qref——机组制冷量，kW

W——机组耗电量，kW·h