液氮直接蒸发制冷系统模糊PID控制方法的数值模拟与实验研究

(1 上海交通大学制冷与低温工程研究所 上海 200240； 2 上海卫星装备研究所 上海 200240)

目前主流制冷方式包括：压缩制冷、电热制冷、吸附制冷、液体气化制冷等，其中压缩制冷由于具有能效比高、可控性好、制冷温区较广等特点应用最为广泛[1-2]。在低温领域(<-100 ℃)，由于压缩制冷的制冷效率较低，为满足大功率低温制冷需求，压缩制冷设备往往体积较大、初投资大且经济性低[3-4]。为达到所需温度及制冷功率，目前主流的一种解决方案是采用低温液体直接气化的制冷方式，使用的低温工质主要包括：液氦、液氮。相比于液氮，液氦制备成本高、制冷温度过低(理论上可达0 K)，应用对象主要为研究实验，在工业应用上仍不普遍[5]。因此，对于空间低温度的大功率制冷需求，采用液氮气化制冷方式更为高效经济。

对于小型热环境室，液氮制冷系统、热环境室的空间均较小，导致热容小，系统空间温度受环境、阀门调节精度等因素影响，仅通过改变液氮流量作为调温方法时，效果往往不尽如意。为了达到较高的控温精度，可以采用电加热作为控制热源，与系统冷源即液氮输入量进行冷热对冲，通过同时调节液氮流量与电加热功率的方式达到较高的控温精度。对于较大空间的液氮制冷系统，系统本身具有大热容、强抗干扰性、长时间滞后等特点，使用外加热源作为辅助控温手段虽然可以提升控温精度，但由于热容较大，采用该方式会导致系统额外损失较多的制冷量，能源经济性较差[6]。因此，对于该类系统，在阀门调控性较好的基础上，可以尝试采用仅通过调节阀门开度改变液氮流量，控制系统温度。

为设计合适的控制策略，有必要对系统控制特性进行详细的分析研究。杜宏鹏等[7]通过对超导腔低温系统建模，研究其降温特性，为制冷系统的实际控制及运行提供理论支持。Peng N.等[8]建立制冷剂部件模型并进行动态模拟，获得系统动态响应特性。研究表明，由于低温制冷系统具有多变量耦合、长时间滞后等特性，实际控制系统较为复杂，控制参数的设定通过预实验整定的方式费时费力。通过建立系统对象模型，结合实际控制策略，进行联合动态仿真，能够大大提高控制系统开发效率[9]。

本文以低温存储系统作为研究对象，建立系统的动态分布参数模型，并基于模糊PID控制方法设计控制策略，以动态分布参数模型为基础，进行模糊PID控制策略的控制仿真，最终将控制策略应用于实际系统，进行实验验证。

1 研究对象及动态仿真模型

低温液氮制冷系统如图1所示，主要包括：液氮杜瓦罐、液氮截止阀、气液换热器、流量调节阀及进出风口等。

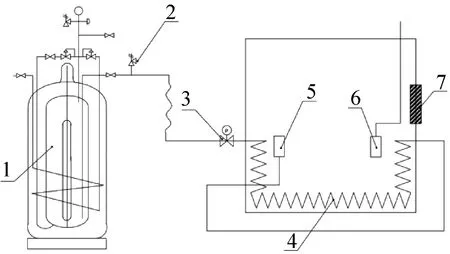
1液氮杜瓦罐；2安全阀；3调节阀；4箱体内部盘管；5入口风道；6出口风道；7观察窗。图1 低温液氮制冷系统Fig.1 Liquid nitrogen refrigeration system

实验系统主要参数为液氮杜瓦罐供液压力、箱体尺寸、液氮盘管尺寸与结构及温度测点位置。其中自增压杜瓦罐最大压力为0.5 MPa；箱体尺寸为1 m×1 m×1 m；液氮盘管总长度为26 m，管径为10 mm，盘绕于箱体壁面处，盘管示意图如图2所示；温度测点位于箱体内部入口风道处。

图2 系统盘管示意图Fig.2 Schematic diagram of coil

1.1 降温系统流程

低温存储系统在不采用外加热源的情况下使用液氮直接蒸发进行制冷，要求实现宽温区的高精度控温。实验系统采用自增压杜瓦罐作为液氮提供设备，液氮自杜瓦罐增压后流出，由液氮调节阀进行流量调节，进入盘绕于箱内的蒸发盘管进行蒸发并对箱体对象进行壁面预冷，完全蒸发后的冷氮气通过入口风管送入箱内，对箱内空间进行降温。

实验系统通过大流量液氮直接蒸发预冷壁面并将蒸发后的低温冷氮气送入箱内，能够实现对箱体的快速降温并减少过程中液氮损耗量。由于未采用辅助热源对出口冷氮气的控制，在减少冷量损耗的同时也增大了控制难度。随着箱体壁面温度的降低，壁面与盘管内液氮换热量迅速减少，当箱体达到目标温度时，对流量调节阀的调控至关重要。当箱体温度达到目标温度后，需要进行系统保温，保温过程中，为了能够稳定控制箱体温度同时防止液氮换热不充分而出液，需要对系统的控制特性进行详细分析。

本文采用基于动态分布参数模型对系统的控制特性进行分析，结合模糊控制策略与PID控制方法实施模糊PID控制策略，并进行了动态模型与控制策略的闭环仿真研究。

1.2 基于分布参数的动态模型

1)模型假设

实验系统中部件较多，且热力学过程十分复杂。为适当简化数学模型，进行如下假设：

(1)采用一维流动模型，忽略管道内流体径向传热与流动特性，即管内流体在流动方向呈一维分布，在同一通流界面具有均一的热力学与流体力学参数。

(2)液氮通过在管内进行蒸发换热，对处于两相共存的液氮采用均相模型假设。

(3)管壁热阻忽略不计。由于管壁较薄，且其热阻阻值与内外侧换热热阻相比很小，可忽略不计。

(4)实验系统温度监控点位于箱体内部出风口处，系统为开式系统，故模型中将箱体与壁面盘管进行统一处理，忽略箱体出口氮气对液氮盘管的影响。

2)管内流动数学模型

系统中液氮仅在管道中进行流动换热，因此系统动态分布参数模型主要以管道内液氮的动态分布参数模型为主，图3所示为简化的管道液氮流动模型。

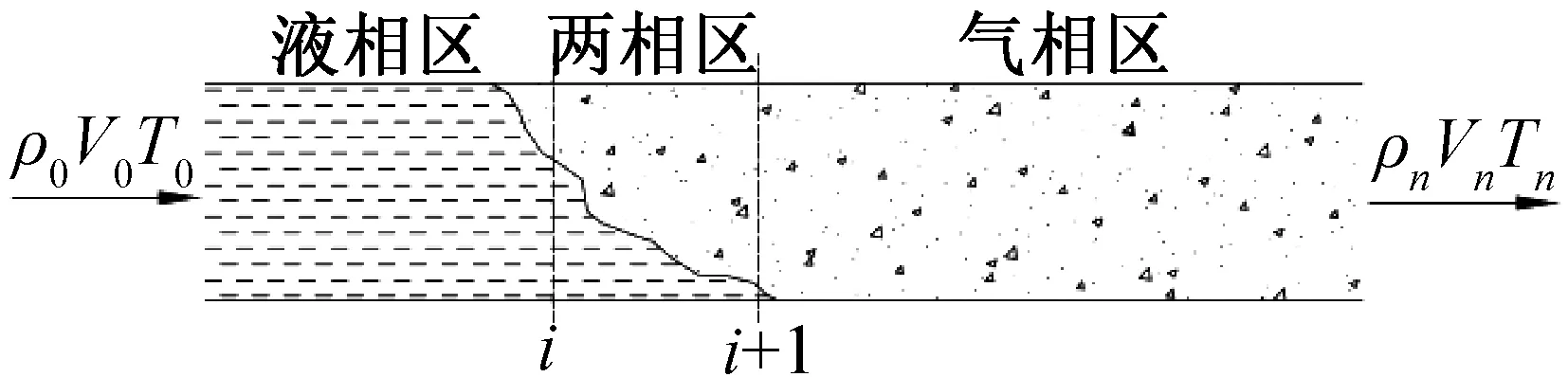
图3 管道液氮流动模型Fig.3 Liquid nitrogen flow model in pipeline

一维管内液氮流动遵循质量守恒、动量守恒及能量守恒方程。

质量守恒方程：

(1)

动量守恒方程：

(2)

能量守恒方程：

(3)

式中：ρ为密度，kg/m3；V为流速，m/s；∂t为时间微分；∂z为管道长度微分；h为比焓，J/kg；Tf为环境温度，℃；Tw为壁面盘管温度，℃；D为管道直径，m；α为液氮对流换热表面传热系数,W/(m2·K)，对于单相对流换热表面传热系数，由Dittus-Boeler换热关联式[10]计算：

Nu=0.023Re0.8Pr0.3

(4)

式中：λ为液氮导热系数，W/(m·K)。

对于两相区，表面传热系数采用Shah的公式[11-12]：

(5)

式中：αTP为两相区表面传热系数,W/(m2·K)；αop为单相区表面传热系数,W/(m2·K)；x为两相区干度。

3)阀门模型

阀门作为系统中唯一可调控器件，其作用是通过改变阀门开度，调节液氮流量，在模型中通过建立其开度与阀门前后压差关联式的方式改变液氮流量，阀门的压差与开度关联式为：

(6)

式中：Δp为阀门前后压力损失，Pa；Q为体积流量，m3/s；G为液氮相对于水的比重，取0.808；R为调节阀开度百分比,%。

4)箱体盘管模型

箱体盘管具有蓄热作用同时能够通过保温结构与外界环境进行换热，箱体盘管能量守恒方程：

(7)

式中：cw为箱体盘管比热容，J/(kg·K)。对于实际箱体盘管存在非均一的特性，为简化计算，采用改变cw的方式对式(7)进行修正计算。

1.3 计算算法

计算过程中，由于流动方程时间常数远小于传热方程时间常数，为保证算法的收敛性、稳定性及高效性，单个时间步长内采用流动、传热分离的方式进行计算[13]。流动方程的计算采用假设入口流速，判断压力是否收敛满足边界条件的方式进行。传热方程的计算通过计算节点换热量，并采用MacCormack方法[14]进行多次预估校正以使节点属性满足能量守恒方程。

2 系统控制策略

2.1 PID控制

低温系统为单输入单输出系统，传统PID控制策略以输入量的偏差、偏差时间微分、偏差时间积分为参数得出输出量。本系统采用传统PID数学描述：

(8)

式中：V(t)为阀门开度百分比，%；Kp为比例调节系数；Ki为积分调节系数；Kd为微分调节系数；eT为温度采集值与设定值的偏差。

根据式(8)可以实现系统的PID自动控制，其控制效果完全由调节参数(Kp，Ki，Kd)决定。对于大多数低温制冷系统而言，由于存在系统热容较大、液氮流量对阀门开度变化的响应时间长、气液两相区位置变化剧烈等因素，为了使传统PID控制策略达到满意的控制效果，往往需要进行较多的预实验与调节参数的整定工作，较为繁琐，且调节参数的整定工作有较高的技巧性。由于PID控制策略的控制效果完全由3个调节参数决定，鲁棒性较差，无法适应系统所处环境(环境温度、供液压力等)的变化。因此，本文结合传统PID控制方法及模糊控制方法，设计一种适合液氮直接蒸发式制冷系统宽温区高精度控温的自动控制策略。

2.2 模糊PID控制器设计

模糊控制方法是一种采用自然语言变量实现的控制方法，无需建立被控对象的数学模型，具有很好的鲁棒性[15-16]。图4所示为模糊PID控制器结构，Tset为系统设定目标温度，模糊控制器以eT及Δ(eT)为输入量，在模糊控制器内首先进行模糊量化处理，将模糊量化处理后的量化值输入至模糊控制规则中进行模糊决策，完成模糊决策后将输出合适的PID调节参数。在得到合适的PID参数的基础上，模糊PID控制器将实现PID控制功能，实现对阀门开度的调整进而调整液氮质量流量，改变系统冷量供应。

图4 模糊PID控制器Fig.4 Fuzzy PID controller

根据Mamdami的最小最大模糊推理方法，采用加权平均解模糊化的模糊控制输出为：

(9)

式中：ΔKa为输出变量增量；yj为输入量模糊子集；ω为隶属度函数。本系统输入输出隶属度函数均采用三角形隶属函数。

输出变量ΔKp模糊控制规则表如表1所示。

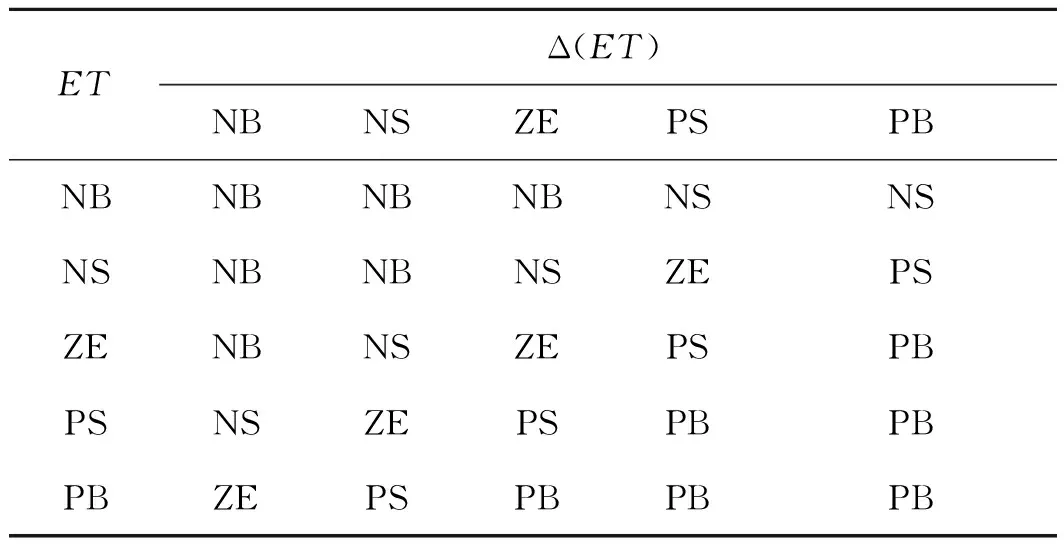
表1 ΔKp模糊控制规则表Tab.1 Fuzzy control rule table of ΔKp

注：ET为温度偏差模糊量化值；Δ(ET)为温度偏差变化率的模糊量化值；负大(NB)、负小(NS)、零(ZE)、正小(PS)、正大(PB)为自然语言变量。

由模糊控制器所得为PID控制器调节参数的增量，故PID调节参数为：

Kp=Kp0+ΔKp

Ki=Ki0+Ki

Kd=Kd0+ΔKd

(10)

结合式(8)～式(10)得到模糊PID控制策略实际阀门输出开度值。

3 仿真与实验结果

3.1 模拟与实验系统方法

控制策略的数值模拟方法与控制策略实际运行方法相同，根据已经建立好的模糊PID控制器，设定好目标温度Tset，将其与模拟的数值结果Tnum共同输入控制器中，由控制器输出对应阀门开度，阀门开度的变化对应其阻力损失的改变，由系统分布动态参数模型进行数值计算，得到模拟结果。

将所得模拟结果Tnum与实验结果Texp进行交叉对比验证，由实验结果验证分布动态模型的准确性，同时根据模拟结果改进模糊PID控制器参数性能。

3.2 仿真与实验结果

根据本文所述模拟与实验方法，进行-50、-80、-140 ℃ 3个目标温度工况下的数值模拟与实验，模拟与实验结果如图5所示。

为定量评价仿真模拟结果的准确性及有效性，定义绝对平均误差SD(℃)及相对平均误差RSD：

(11)

(12)

根据式(11)、式(12)计算仿真与实验结果降温过程及全过程绝对平均误差及相对平均误差，计算结果如表2所示。

上述3种目标温度工况，采用相同的模糊PID控制策略，仿真条件下箱体温度随时间的变化规律与实验结果基本相同，且达到目标温度时间相当。由表2可知，仿真与模拟结果在全度过程中的相对平均误差在2.6%～3.0%范围内，降温过程中相对平均误差在6.4%～7.8%范围内，相对平均误差受目标温度工况的变化影响较小。随着设定温度的减小，降温过程与全过程的绝对平均偏差均呈增大趋势，-140 ℃时降温过程及全过程的绝对平均偏差最大分别为6.9、3.8 ℃。由于实际实验过程中存在较多不确定因素，可以认为通过本文的动态分布参数模型与模糊PID控制联合仿真的方式能够较好地表现系统的降温特性及模糊PID控制器的控制特性，模型具有较高的准确性及可靠性。

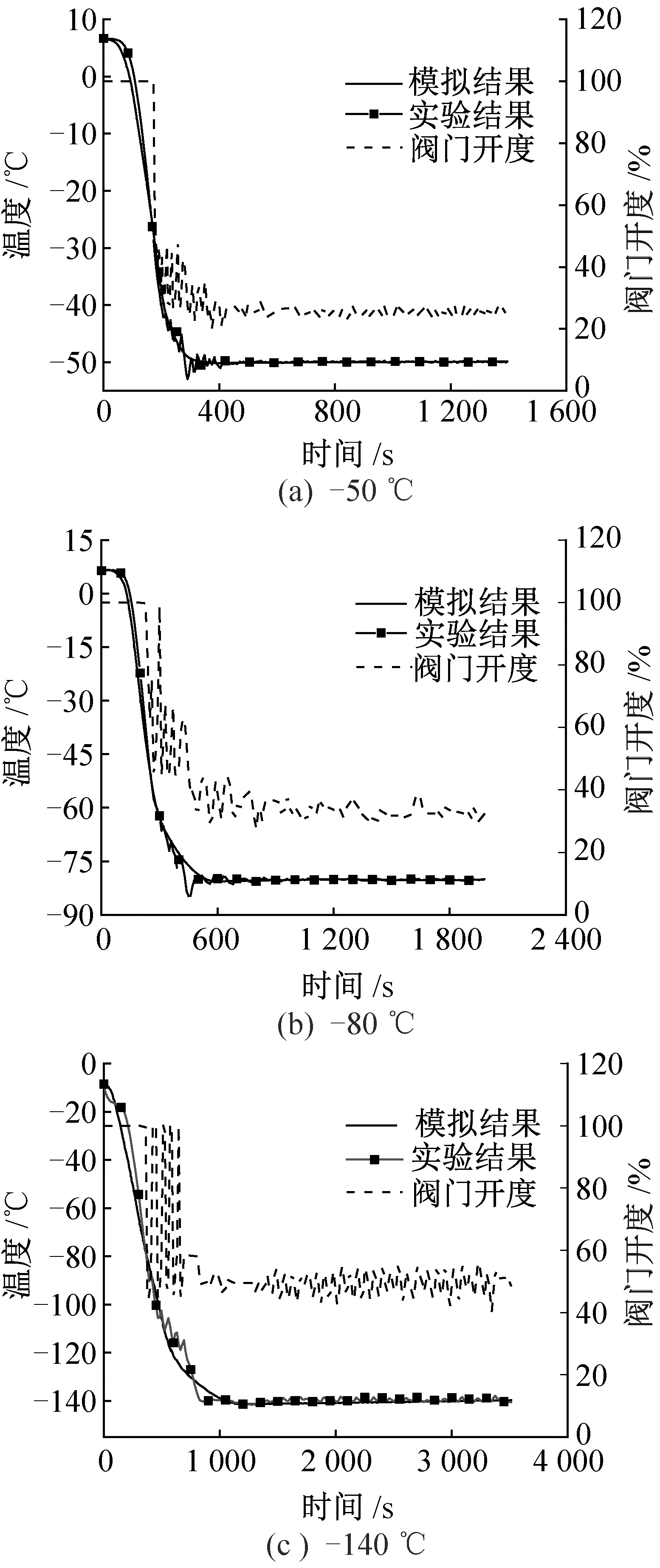
图5 数值模拟与实验数据对比Fig.5 Comparison of numerical simulation and experiment results

工况/℃降温过程全过程SD/℃RSD/%SD/℃RSD/%-502.17.61.12.6-803.26.41.92.7-1406.97.83.83.0

由图5(a)可知，当目标温度为-50 ℃时，超调温度为2.9 ℃，振荡调节时间为126 s，温度波动在-0.5～0.5 ℃范围内；由图5(b) 可知，目标温度为-80 ℃时，超调温度为4.7 ℃，振荡调节时间为372 s，温度波动在-1.0～1.0 ℃范围内；由图5(c)可知，目标温度为-140 ℃时，由于液氮过冷度较小，且为防止出口处流出液氮，控制器输出阀门开度较早地进行调小，此时无降温过程无明显的温度超调与振荡，温度波动在-2.0～2.0 ℃范围内。故本文设计的模糊PID控制器完全能够满足低温液氮直接蒸发制冷系统各工况下的控制要求。

4 结论

本文建立了低温液氮直接蒸发制冷系统的一维动态分布参数模型，设计了一种满足该类型系统控制需求的模糊PID控制策略。在3种不同目标温度-50、-80、-140 ℃的工况下，进行控制策略与系统模型的联合数值模拟和实验，得到如下结论：

1)模拟结果与实验结果吻合度较高，3种工况下平均相对误差小于5%，最大相对误差仅为7.8%，表明该模型能够有效反映模糊PID控制策略应用于低温液氮制冷系统的控制特性，可以实现以模型代替实际物理对象进行控制策略的参数预整定工作，大大减少了在研制低温液氮制冷系统时控制系统的开发成本。

2)模糊PID控制策略取得了较好的控制效果，在-50、-80、-140 ℃目标温度工况下，稳态温度波动范围分别为±0.5、±1.0、±2.0 ℃，控制策略在低温工况下具有较好的稳态控制特性，能够实现该类型系统较宽温区的高精度控温。