泥沙冲刷模拟的FLOW-3D数值方法研究
黄佳丽 ,倪福生 ,顾磊
(1.河海大学疏浚技术教育部工程研究中心,江苏 常州 213022;2.河海大学机电工程学院,江苏 常州 213022)
0 引言
泥沙冲刷是很多水利工程中常见的现象,常见于桩柱冲刷、管道局部冲刷及水射流冲刷等。黄雄合等[1]利用动床模型水槽试验,研究了桩柱周围局部床面由平整发展到冲刷坑的过程,获得了各工况下冲刷坑的形态参数;姜萌等[2]采用物理模型试验方法,探索了泥沙中值粒径、立管-桩倾斜角度及水深等对海洋平台立管系统底部冲刷坑的影响。张浩等[3]在粗沙沙床条件下对二维垂向淹没射流冲坑深度进行了实验研究,研究了射流速度对动态坑深的影响;顾磊等[4]探究了双股射流冲刷时喷嘴间距对冲刷坑形、冲坑深度和冲坑截面积的影响。
通过对前人的研究以及相关试验过程的分析发现试验研究存在很多缺点:在试验前对冲刷的泥沙的准备有很高的要求,每次都需要耗费大量的时间;试验过程中无法观测试验现象,尤其是泥沙粒径很小时,射流冲刷流场很浑浊,无法对其内部机理进行捕捉;冲刷结束后需要缓慢将水排放,不仅耗时而且还对冲坑有一定的影响;最后在对冲坑进行测量时,冲坑表面会有很多的泥沙堆积,对其静态坑深的结果有影响,同时由于观测不便,动态冲坑深度的变化无法准确的进行测量。
近年来,在与泥沙冲刷的有关数值模拟中,FLOW-3D软件应用较为广泛。与试验相比,数值模拟方法具有省钱、省力和灵活性较大等优势,由于试验参数的改变方便,对于大量重复试验能够轻易完成[5]。周丽丹等[6]采用泥沙冲刷模型和湍流模型k-ε相结合,对均匀来流海底管道冲刷过程进行分析,发现了冲刷坑的形成原因及冲刷坑最大深度发生位置;王建军等[7]采用FLOW-3D软件基于泥沙冲刷模型进行了数值模拟,发现数值模拟结果与试验结果较为吻合;顾磊等[8]应用FLOW-3D软件研究了双喷嘴射流冲刷砂床时冲坑形态的发展过程以及冲坑形态、深度和面积随喷嘴间距的变化规律,并通过模型试验对其进行了验证。
本文在前人研究的基础上发现:数值模拟软件FLOW-3D在泥沙冲刷的模拟中有较完善的模型和方法,但是在泥沙冲刷领域对其泥沙模型关键参数设置的研究较少,大多采用经验值或相互参考,较多文章中参数几乎一致,没有将模型参数与试验可以获得参数进行较好的关联。所以本文采用FLOW-3D数值模拟的手段从射流冲刷泥沙出发,对泥沙模型中的关键参数进行了探究,以期为该软件在泥沙冲刷模拟上的应用提供一定的参考。
1 理论模型
1.1 控制方程
连续性方程

式中:VF为流体流动部分的体积分数;ρ为流体密度;RDIF为湍流扩散项;RSOR为质量源项;u、v、w分别为在坐标方向(x、y、z)上的速度分量;Ax、Ay、Az分别表示流体在x、y、z方向的投影面积;R和ξ为与坐标系统的选择相关的系数。
动量方程

式中:Gx、Gy、Gz为流体重力加速度;fx、fy、fz为黏滞加速度;bx、by、bz为流体通过多孔介质或导板的能量损失。
1.2 泥沙模型
在泥沙模型中,泥沙在水中以悬移质和推移质两种状态存在。由于单个泥沙颗粒周围的流体动力和交界面处的边界层难以计算,所以须使用经验模型。
坡面法线与重力方向的夹角悬移质计算模型中,泥沙的上升速度由式(3)计算:
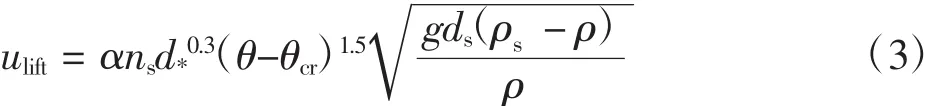
式中:ulift为用来计算由底沙转化为悬沙的泥沙量;α为挟带系数;ns为沙床面的外法线方向;d*为泥沙颗粒的无量纲粒径;θ为床面希尔兹数;θcr为临界希尔兹数;g为重力加速度;ds为泥沙颗粒的直径;ρs为泥沙的密度。
床面希尔兹数θ由床面剪切应力计算:

式中:τ为床面剪切应力。
临界希尔兹数θcr基于Mastbergen和Von den Ber[9]提出的经验模型,以及Shields-Rouse方程[10]来预测。
推移质计算基于Meyer-Peter和Muller[11]的计算模型,床面的单宽体积推移质输沙率由该模型预测可得,公式如下:

式中:β是推移质系数;Φ是无量纲的推移质输沙率;Φ与单宽体积推移质输沙率qb的关系是:

由式(6)可以计算出每个单元中各个时刻的单宽体积输沙率。
2 网格质量
网格是数值模拟计算的基础,网格划分决定了计算域的划分和控制方程的离散程度,其尺度决定了计算的稳定性和准确度。因此在数值模拟中对于网格的探索十分必要。在使用FLOW-3D进行水射流冲刷泥沙的数值模拟时,对网格的探索如下。
由于建立模型的简单,可以直接在软件内进行绘制,网格覆盖整个模型区域,为保证所有结构都能被识别,在关键部位增加网格线,进行局部加密。
在所建模型中,喷嘴的结构是圆柱体,而FLOW-3D中的网格形式为结构式有限差分网格,单元格呈现为矩形棱柱。不同于CFD常见的贴体网格,FLOW-3D的网格对复杂几何的描述精度较差,必要的局部加密才能实现较好的描述,网格覆盖整个模型但因其全结构式,有很高的计算效率,累计的数值误差较小。
将尺寸相对于整体结构较小的喷嘴进行加密处理。图1为3种相邻网格尺寸比情况下,划分的网格经过favor检查之后的喷嘴内径与外径的识别情况,深色区域表示所识别的固体材料。
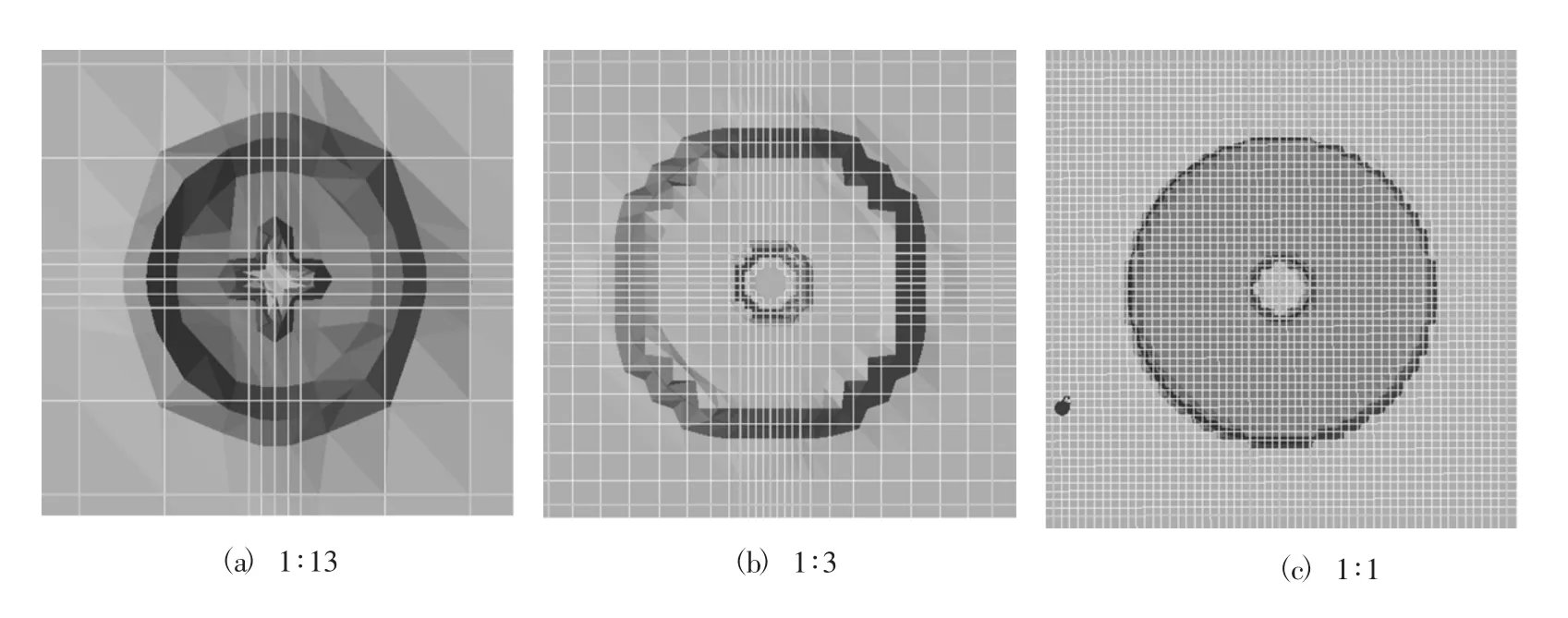
图1 不同网格尺寸比的喷嘴识别情形Fig.1 Nozzle recognition under different mesh size ratios
由图1中可以看出相邻网格尺寸比越小,识别的喷嘴结构越圆。在相邻网格尺寸比较大时,喷嘴只在网格的节点以方形结构显示,所以在进行网格加密时,同一坐标方向上相邻两个结构的网格宽度之比,应控制在一定的范围之内,一般要求不超过1.25。但考虑计算效率等因素,经过对各种网格尺寸比的探索,发现比值在1.0~2.0以内时,计算结果的数值没有明显的误差。此外单个网格在3个坐标方向上的宽度比例也应该保持在合适的范围以内,一般不超过3.0,尽可能接近一致。
因此在对实际问题进行数值计算时,其网格比例通常是不确定的,需要通过不断的调试和比较,才能获得吻合具体问题的网格。
本文研究模型较为简单,所得出的加密尺寸仅供参考,其他不同情况下的模型网格还是需要大量探索。
3 泥沙模型关键参数
在水射流过程中,冲刷为一种随机现象,泥沙会呈现出悬浮、扩散、迁移和沉降等状态,FLOW-3D软件中的泥沙模型可较好地预测泥沙的各种状态,模拟出与试验吻合的泥沙运动状态。泥沙模型参数设置对泥沙的悬浮、扩散以及堆积情况有很大影响,其中影响最大的是泥沙临界体积分数Cv、泥沙的水下休止角φ、泥沙挟带系数α和推移质系数β。由于研究的泥沙粒径不同,各种参数的具体设置也不同。采用单因素分析法,以0.09 mm粒径的沙为例,每次只改变其中1个参数,观察该参数对模拟过程的影响。
3.1 泥沙临界体积分数Cv
泥沙的临界体积分数Cv对泥沙冲刷形态有很大影响,其设置范围为(0,1)。分别设置体积分数为0.1,0.3和0.9,其他参数保持默认,模拟结果如图2所示。
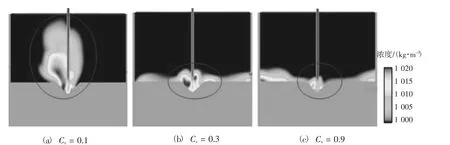
图2 不同泥沙体积分数的射流冲刷浓度分布Fig.2 Distribution of jet scouring concentration under different maximum packing fractions
由图2中可看出,泥沙临界体积分数值不同时,射流冲坑深度相差不大,但是泥沙悬浮量有很大不同,临界体积分数为0.1时悬浮泥沙扩散最高,当其值增大时悬浮泥沙扩散高度降低,且沿着沙床方向移动,运动过程呈现为悬移质与推移质的交换过程。即临界体积分数越大,悬浮的泥沙量越少。总结前人关于FLOW-3D的研究[11]以及在对射流冲刷泥沙试验中需要研究的实际参数的比较,发现泥沙临界体积分数与试验中泥沙的孔隙率有关,泥沙临界体积分数=1-泥沙孔隙率。
当研究的泥沙粒径不同时,泥沙临界体积分数不同。对于不均匀泥沙,其值会较大;而对于均匀泥沙或泥沙颗粒形状不规则,其值会较小。
3.2 泥沙的水下休止角φ
在射流冲刷完成后,冲坑呈现为有一定角度的斜坑,在模拟时,可以通过设置泥沙模型中水下休止角的参数模拟冲坑角度。在对该参数进行设置时发现,休止角设置为某角度最终呈现的模拟效果就是该角度,十分直观。图3为分别将参数值设置为32°和45°时的冲坑截面图。

图3 不同水下休止角的射流冲坑形状Fig.3 The shape of jet scouring pit at different underwater angles of repose
从图3的冲坑角度来看,图3(a)设置为32°,模拟结果显示休止角为31°;图3(b)设置为45°,模拟结果显示休止角为45°,可见最终冲坑的休止角与所设置的参数值一致,但如此并不符合实际情况,试验时得到的冲坑不是一个确定的角度。所以在设置泥沙水下休止角时要先对所试验的沙粒进行水下休止角测量,同时考虑泥沙粒径和水下斜坡效果的影响,如此才能更好地贴合实际情况。
3.3 泥沙挟带系数α
泥沙挟带系数α控制该沉积物受力大于临界剪切应力时侵蚀的速率。挟带系数可以用于缩放冲刷率。零值完全关闭挟带模型。图4为挟带系数分别为0.001、0.018和0.4时的射流冲刷浓度分布情况。
在进行模拟时,只改变挟带系数的值,其他参数保持为默认值,从图4可以看出,图4(a)中冲刷坑深以及冲刷宽度都很小,悬沙没有沉降而是随着水流的上升全部上升,此情况不符合实际情况;图4(b)中,冲刷坑深与冲坑宽度比图4(a)有明显增加,悬沙在涡流挟带下在两侧交替增多,两侧悬沙形态呈现一定的对称性,有沉积现象且泥沙向四周扩散;图4(c)中冲坑深度与冲坑宽度远大于前两种情况,泥沙起动之后直接向四周扩散,没有出现明显的泥沙随涡流悬浮运动的状况。综合3种情况可以看出,挟带参数的选择对于泥沙运动模拟情形有很大的影响。在模拟过程中,挟带模型的速度方向是垂直于沙面向外的,该数值越大对底床冲刷的速度越快,随冲刷起动的沙更多。

图4 不同挟带系数的射流冲刷浓度分布Fig.4 Distribution of jet scouring concentration under different entrainment coefficients
3.4 推移质系数β
推移质系数β在床载荷传输速率方程中使用,并控制该床载荷传输发生在剪切应力比临界剪切应力更高时的速率。不同推移质系数下射流冲刷浓度分布如图5所示。
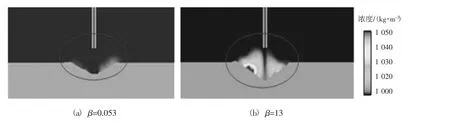
图5 不同推移质系数的射流冲刷浓度分布Fig.5 Distribution of jet scouring concentration under different bed load coefficients
由图5可以看出推移质系数小时,泥沙悬浮量很小,在沙坑两边有轻微堆积泥沙现象,当推移质系数较大时,冲刷沙坑中泥沙悬浮明显,且沙坑两边泥沙堆积较为明显。可以看出:推移质模型中泥沙的运动方向是沙面附近的水流方向,推移质系数值越大,沉积物沿河床的传输量越大,研究发现[11]从低运输的5.0到非常高的沙运输的13.0的值,沙子和砾石的典型报告值为5.7,在对推移质系数进行设置时可以此为参考。
4 结语
本文应用FLOW-3D软件中的泥沙冲刷模型,对垂直水射流冲刷泥沙进行了数值模拟。本文的研究可以对FLOW-3D在泥沙冲刷的应用提供一定的参考。
1)FLOW-3D软件在用于水射流冲刷的数值模拟可以与试验结果有较好的吻合。
2)网格加密时,需要将相邻网格比以及网格本身3个坐标方向上的宽度比保持在合适的比例,且需要经过不断的调试和比较才能获得计算时间短且符合试验的结果。
3)在泥沙参数设置中,泥沙的临界体积分数越大,悬浮的泥沙量越少;水下休止角则需要进行试验验证;挟带系数越大,随冲刷起动的沙更多;推移质系数越大,沉积物沿河床的传输量越大。

