考虑探测效能的有限时间协同制导方法
张帅, 郭杨, 王仕成, 王少博
(火箭军工程大学 精确制导与仿真实验室, 陕西 西安 710025)
0 引言
近年来,随着飞行器动力系统的不断改善以及拦截任务的多样化,单一飞行器相对于机动目标已不再具有绝对的拦截优势,而多飞行器协同作战理念越来越受到重视。在网络化、体系化作战背景下,通过信息交互和共享,多飞行器协同能够有效增强探测和制导效能。因此,多飞行器协同拦截方式对于提高拦截成功率具有重要的现实意义[1]。
相比于单一飞行器,多飞行器协同探测能够更有效地获取目标相对运动信息,为制导控制系统提供更精确的量测数据。近年来,学者们基于多传感器信息融合和滤波方法对协同探测中的数据融合问题进行了广泛研究。文献[2]针对单架预警雷达存在探测盲区问题,基于累积发现概率准则提出了多架机协同探测航线优化方案,扩大了探测的覆盖区并提高了探测精度;文献[3]针对多传感器对多目标进行协同探测和跟踪问题,提出了一种改进无迹卡尔曼滤波算法,提高了对多个目标的跟踪精度;文献[4]针对多架预警机对目标区域协同探测问题,基于多源信息融合技术提出了两种协同方案,通过实时估算两种方案探测覆盖区优化了飞行航迹;文献[5]针对静止目标,基于最优控制理论提出了一种增强协同探测效能的最优制导律,但该方法只定性地描述了探测效能与制导参数的关系,不适用于拦截机动目标。从公开发表的文献看,目前研究大多是将探测和制导环节分开考虑,对于协同探测的研究也主要侧重于基于状态估计和滤波算法的多源信息融合[6-7]。
在协同制导方面,拦截时间一致、控制终端拦截角和不同通讯拓扑条件下的协同制导问题受到了广泛关注。文献[8-10]针对多飞行器协同拦截时间一致性问题,考虑到不同的通信拓扑结构,基于变参数比例导引方法提出了一种时间协同制导律。但该制导方法需要事先约定制导时间。此外,为实现对加固目标的多角度饱和攻击,文献[11-12]将不同落角约束条件考虑到制导设计中,实现了带有不同角度的协同拦截。为有效拦截高机动目标,文献[13-16]采用多飞行器合作拦截方案,在制导设计时通过施加一个拦截角来有效增强协同探测效能。文献[17]通过建立一对一拦截模型,基于最优控制理论设计了一种协同探测与制导一体化设计方法,在单飞行器对目标进行拦截过程中施加拦截角,进而实现了稳定探测和制导构形的目的。值得一提的是,上述研究大多未考虑制导律有限时间收敛问题。实际上,在进行制导设计时,不仅要使所设计的制导律实现预定的作战意图,还应该考虑制导律有限时间收敛特性。
多飞行器协同拦截是典型的有限时间问题,拦截器制导指令必须在有限时间内完成,拦截过程中所关心的性能指标也都在有限时间内才有意义。在保证制导律有限时间收敛时,过载指令往往过大而不具有执行性,文献[18]为了解决这一问题,设计了一种制导方法,不仅可以保证视线角速率在有限时间内收敛到0 rad/s,还可以保证在制导过程中加速度不超过最大物理限制;文献[19-21]针对机动目标突防问题,基于有限时间控制理论提出了一种最优机动策略,该制导方法保证了制导律在有限时间内收敛;文献[22-23]针对机动目标,在Lyapunov稳定理论基础上设计了一种制导方法,该方法可以保证制导律有限时间Lyapunov稳定。基于上述成果可知,在有限时间框架下进行制导设计更切合实际应用。
综上所述,由于飞行器构形能够影响协同探测效能进而影响制导精度,而制导指令能够实时影响飞行轨迹进而影响拦截构形,因此协同探测和制导两个环节是紧密联系、互相影响的,在进行制导设计时充分考虑协同探测效能是十分必要的。此外,一些现代制导设计方法,如最优控制、H∞鲁棒控制等,在制导时间趋于无穷时能够取得较好的效果,但在有限时间内可能存在保守性过大或者制导效果较差的问题。基于上述分析可知:1)多飞行器协同探测与制导环节是紧密联系的,而目前研究多数将探测和制导环节分开来考虑,在进行制导设计时没有充分考虑探测效能;2)多飞行器协同探测与制导问题是典型的有限时间过程,在有限时间框架下探索协同探测制导方法具有更强的针对性和实用性;3)为保证较好的探测和制导效果,飞行器在不断调整机动过载过程中必然会受最大加速度的约束,而目前研究较少将加速度抗饱和性能考虑在制导设计过程中。
本文基于有限时间理论,提出了一种增强协同探测效能的协同制导方法,旨在制导设计的有限时间内检验协同探测效能。该方法充分考虑制导律有限时间收敛性能,能够保证协同制导律在有限时间内收敛到预定状态且加速度不超过最大物理限制,仿真结果验证了所提方法的有效性。
1 问题描述
1.1 飞行器相对运动建模
2个拦截器协同拦截机动目标场景如图1所示。图1中:Oxy为惯性坐标系;P1和P2表示2个拦截器;E表示目标飞行器;vP1、vP2、vE和aP1、aP2、aE分别表示飞行器速度和视线法向加速度;qP1P2、qP2P1、qP1E、qP2E表示视线角;rP1P2、rP1E、rP2E表示飞行器之间的相对距离;与各飞行器相关的变量分别用下标P1、P2和E表示。
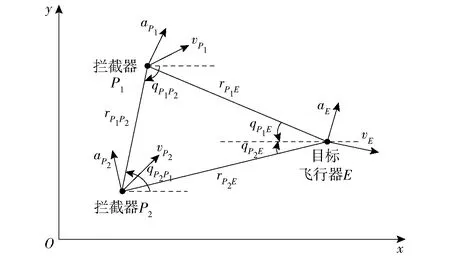
图1 2个飞行器协同拦截目标飞行器示意图Fig.1 Schematic diagram of two missiles cooperatively intercepting a target
在拦截过程中,拦截器与目标飞行器之间的相对运动可以分解为沿视线方向的径向运动和沿垂直视线方向的视线旋转运动。一般情况下,在保证拦截器和目标飞行器径向相互接近情形下,控制末端视线角速率收敛到0 rad/s即可实现有效拦截。由于拦截器的任务需求和机动优势,拦截器与目标飞行器之间总能够保持相互接近,此时成功拦截的关键是对视线旋转运动进行制导控制设计。
基于坐标变换,忽略视线角速率2阶小量,在垂直视线方向可以得到拦截器1与目标飞行器之间的视线旋转运动方程[24]为
(1)
同理,也可以得到拦截器2与目标飞行器之间的相对运动方程为
(2)
在拦截器与目标飞行器接近过程中,由于末制导时间较短,拦截器与目标飞行器之间的径向运动变化较缓,拦截器与目标之间的拦截时间[24-25]可近似为
(3)
式中:rP1E(0)和rP2E(0)分别表示2个飞行器之间的初始相对距离;vP1E和vP2E表示接近速度。
1.2 飞行器动力学建模
飞行器过载指令是由飞行控制系统实现的。过载响应时间决定着飞控系统对过载指令的响应品质,它是飞控系统最重要的性能指标。考虑飞行器均具有1阶动力学特性:
式中:a为飞行器实际加速度;τa为过载响应时间;aC为飞行器制导指令;s为频域自变量。假设各飞行器具有1阶动力学特性,由上式可得
(4)
1.3 协同探测模型
在协同拦截过程中,假设拦截器配备有高精度的导航定位设备和相应的红外角度传感器,2个拦截器能够精确地获得自身的方位信息并能够进行实时通讯,但不能精确获得目标飞行器的方位信息,即2个拦截器能够精确地获得彼此间的相对距离信息rP1P2和视线角度信息qP1P2、qP2P1,但对目标的方位量测包含一定的误差。
2个拦截器构成了测量基准线,由此可以对目标飞行器进行协同探测。假设拦截器对目标的角度探测量包含量测噪声,即PiE=qPiE+σPiE. 其中量测噪声σPiE是相互独立的高斯白噪声,即期望为标准差。根据图1所示的几何位置关系和三角定位原理,可以解算出拦截器与目标之间的相对距离[17]为
(5)
由(5)式可知,解算的相对距离信息包含一定的量测误差。这里假设PiE=rPiE+σPiE,rPiE,其中σPiE,rPiE是相对距离测量误差,且
对(5)式求导,可以得到相对距离探测误差为
(6)
由图1和(6)式可知,协同探测误差与2个拦截器和目标之间的视线分离角|P1E-P2E|直接相关。当视线分离角|P1E-P2E|变小时,量测误差将增大。考虑一种极端情况,当视线分离角趋近于0°(即3个拦截器共线飞行)时,此时误差非常大,进而淹没了真实值。因此,在协同拦截过程中设计合理的协同制导律以调制视线分离角,可以有效增强协同探测效能、减小相对距离探测误差。
1.4 考虑探测几何构形的协同制导问题描述
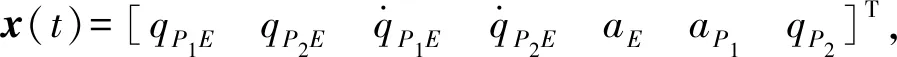
(7)
y(t)=C(t)x(t),
(8)
式中:A(t)=
G(t)为相应的干扰传递矩阵,G(t)=[0 0 0 0 1/τE0 0]T;u(t)为控制输入,u(t)=[aP1CaP2C]T,即需要设计的协同制导律;目标飞行器加速度指令aEC视为外界输入变量;x(t)为状态变量;y(t)为系统评价输出;C(t)为相应的输出矩阵;t为制导时间。
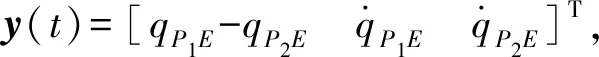

由于拦截器加速度存在最大物理过载限制,可表示为
|aPi|≤aPimax.
由此,通过状态方程(7)式和(8)式即建立了包含相对距离、视线角等探测信息的协同拦截模型。
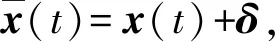
(9)
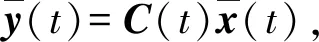
(10)
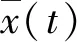
通过引入系统状态修正量,可将视线分离角约束条件加入系统状态方程中,基于探测和制导需求设计带有视线分离角约束的协同制导律,进而增强协同探测和制导效能。
对于系统方程(9)式和(10)式所描述的协同拦截模型,将目标飞行器的机动视为外部干扰输入,制导设计的最终目标是设计合适的协同制导律u(t),使系统状态和输出满足以下约束条件:
式中:tf为制导终时时刻。上述约束条件具体为:设计u(t)使视线分离角收敛到预置的值、视线角速率收敛到0 rad/s,且拦截器加速度不超过最大物理限制,从而达到增强协同探测效能并进行有效拦截的目的。
2 考虑探测构形的有限时间协同制导方法
由于协同探测和制导过程必须在有限时间内完成,且解算的制导指令也是在有限时间内才有意义,因此在有限时间框架下寻求协同制导设计方法更符合实际应用。
本节首先介绍有限时间理论基本知识,然后给出有限时间有界条件下有限时间输入输出稳定的充分条件,最后基于状态反馈控制方法给出有限时间协同制导律设计和解算方法。
2.1 有限时间有界和输入输出稳定定义
定义1有限时间有界[26]。对于系统状态方程
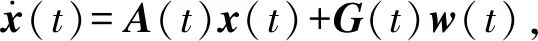
(11)
如果对于∀t∈[0,T],系统(11)式满足以下条件:
则称此系统关于(T,R,Q(t),S1)有限时间有界。式中:w(t)为外部干扰;R、Q(t)、S1分别为预先给定的适当维数的正定度量矩阵;R用于度量初始状态;Q(t)用于度量系统状态,由系统状态需求决定;[0,T]为有限时间区间。
定义1描述了在初始状态和外界有界干扰的影响下,系统状态在有限时间内的稳定性能。有限时间有界性能与度量矩阵R、Q(t)、S1的选取有关,是对系统状态在有限时间区间稳定性的动态描述。
定义2有限时间输入输出稳定[26]。对于线性系统(12)式和(13)式,假设x(0)=0,
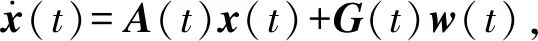
(12)
y(t)=C(t)x(t),
(13)
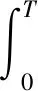
由定义2可知,有限时间输入输出稳定是指在给定的有限时间区间内,当系统外部输入满足范数有界约束时,系统评价输出亦范数有界。有限时间输入输出稳定主要用于表征系统输出在有限时间内对外界有界干扰的镇定能力,与传统的无限时间框架下的Lyapunov输入输出稳定是两个独立的概念。
2.2 有限时间有界条件下有限时间输入输出稳定
基于文献[27]的研究成果,本文给出系统满足有限时间输入输出稳定的充分条件。
引理有限时间输入输出稳定充分条件[27]。对于线性时变系统(12)式和(13)式,在有限时间[0,T]内,如果存在1个对称正定的矩阵函数P(t)∈Rn×n,使得如下2个不等式同时成立:
(14a)
P(t)≥CT(t)S2(t)C(t),
(14b)
则系统(12)式和(13)式关于(T,S1,S2(t))有限时间输入输出稳定。
下面基于2.1节的基础知识,以定理形式给出系统满足有限时间有界条件下输入输出稳定的充分条件。
定理1有限时间有界条件下输入输出稳定。对于线性时变系统(12)式和(13)式,在有限时间[0,T]内,如果存在1个对称正定的矩阵函数P(t)∈Rn×n,使得如下3个不等式同时成立:
(15a)
P(t)≥max{2Q(t),CT(t)S2(t)C(t)},
(15b)
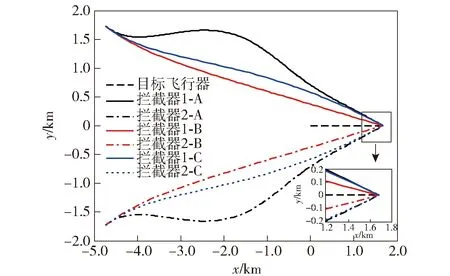
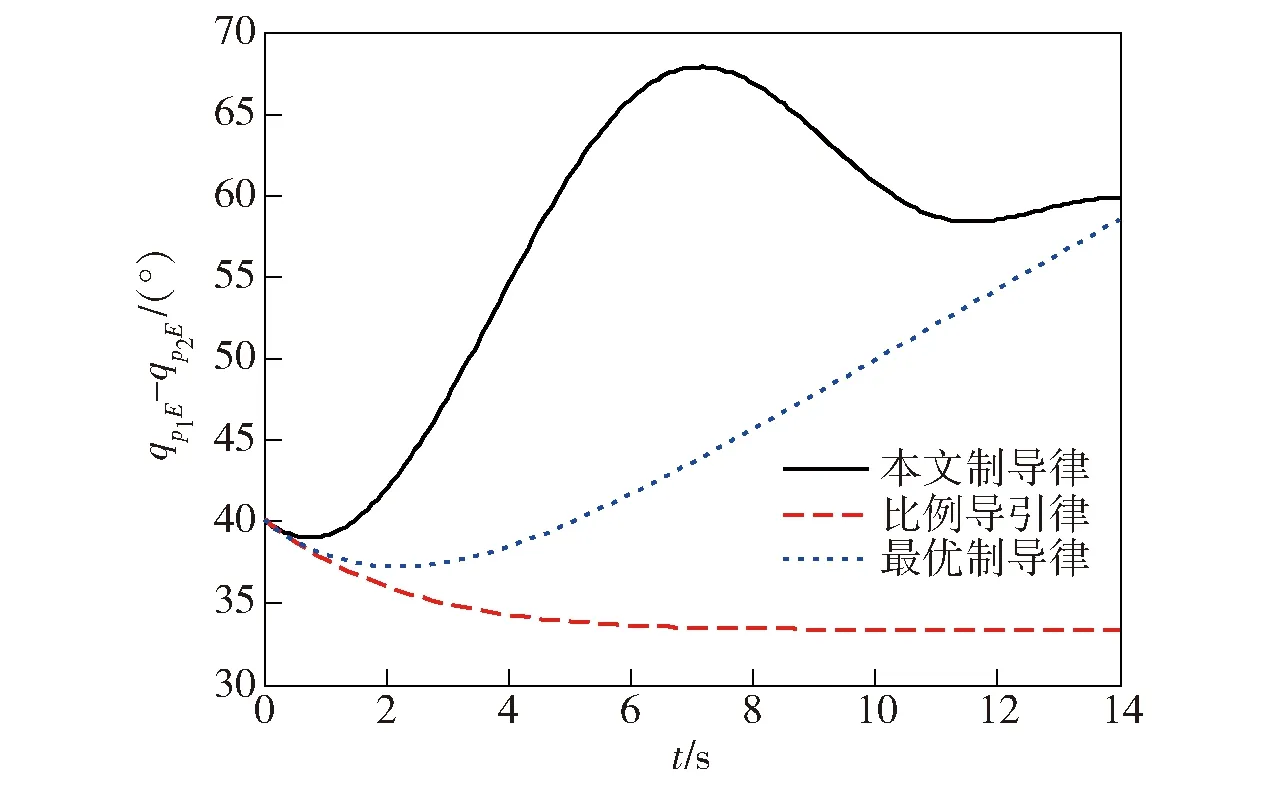
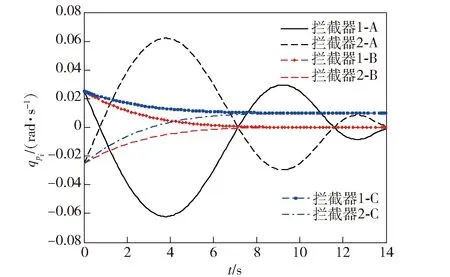
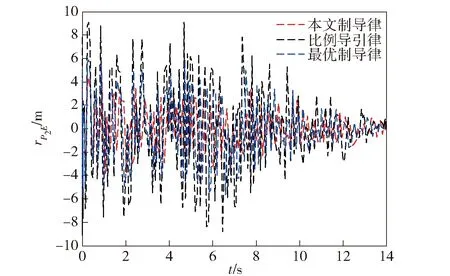
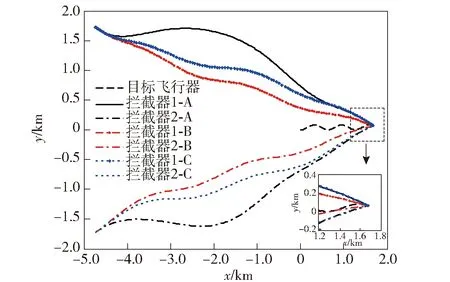
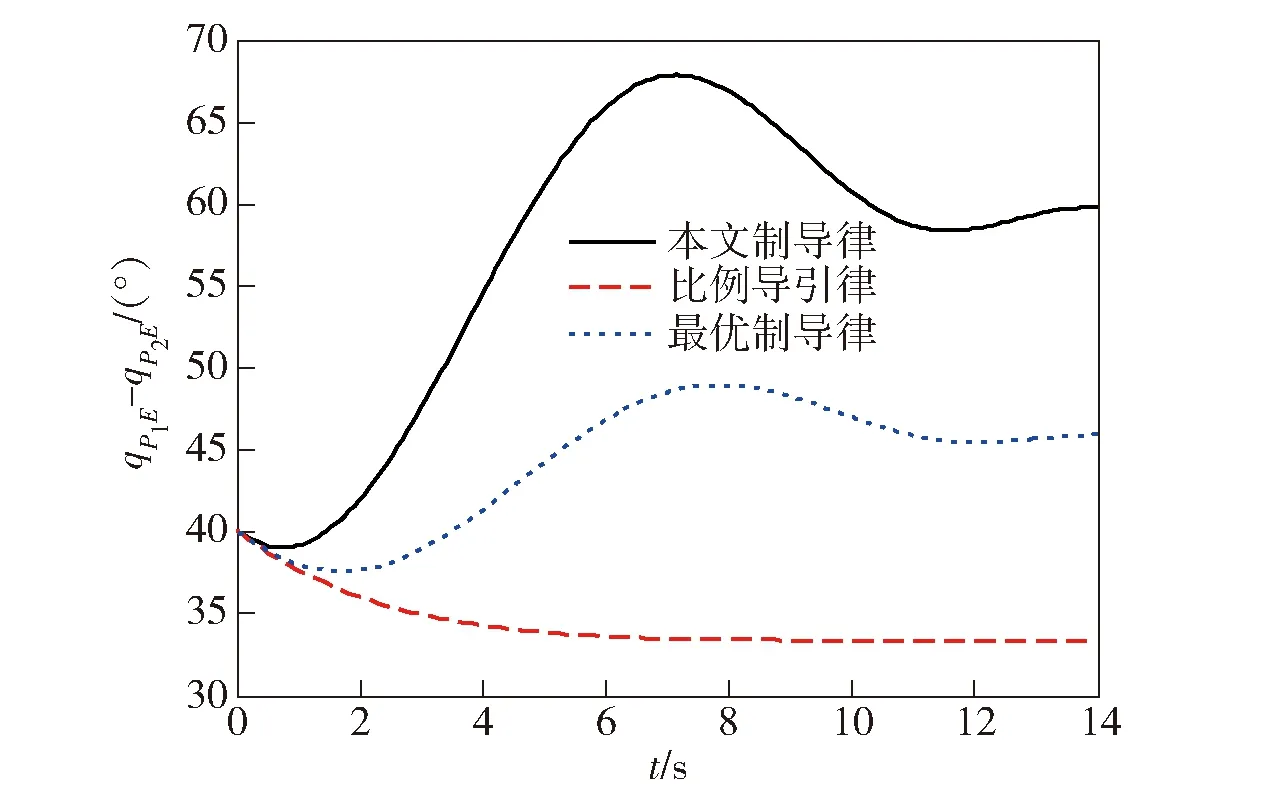
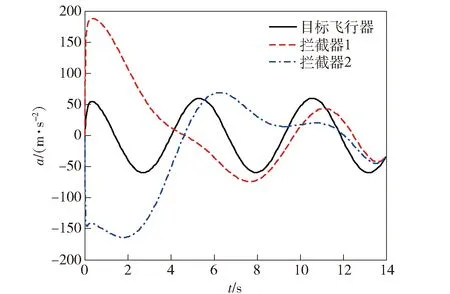
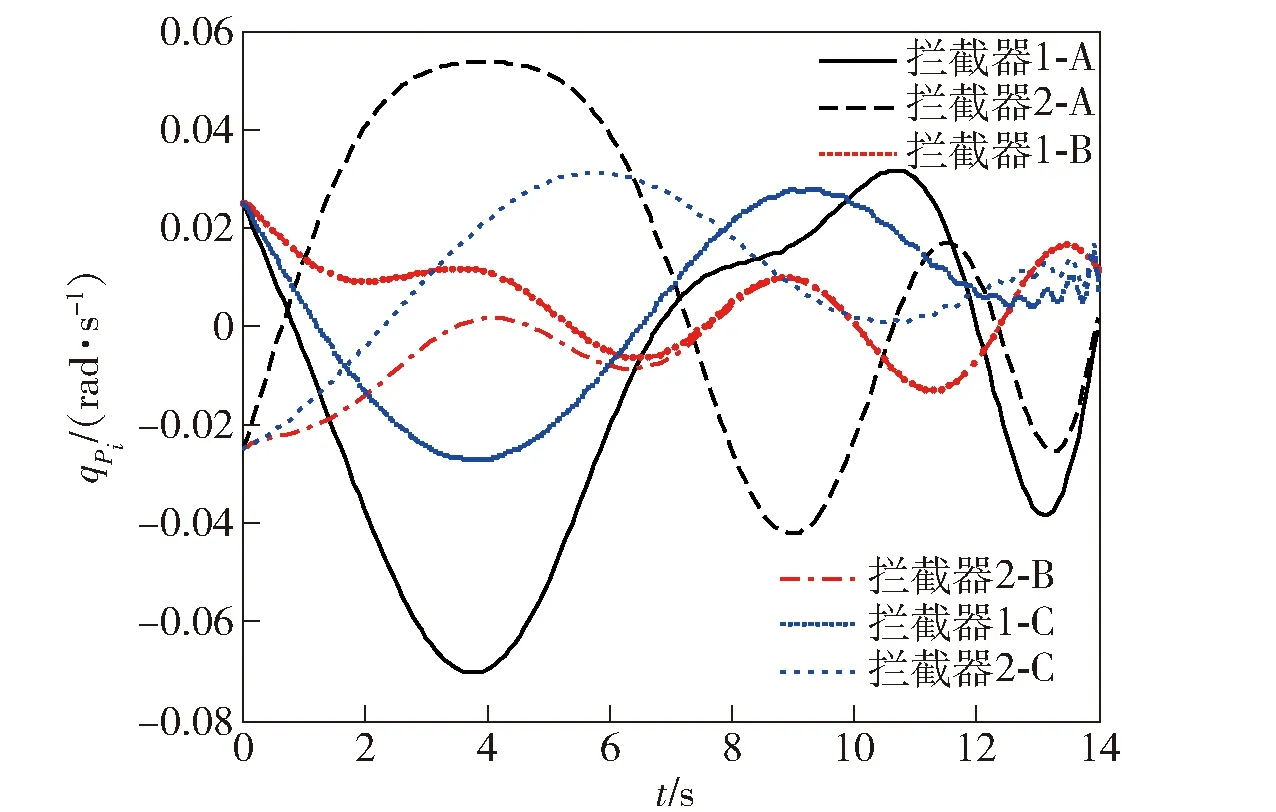
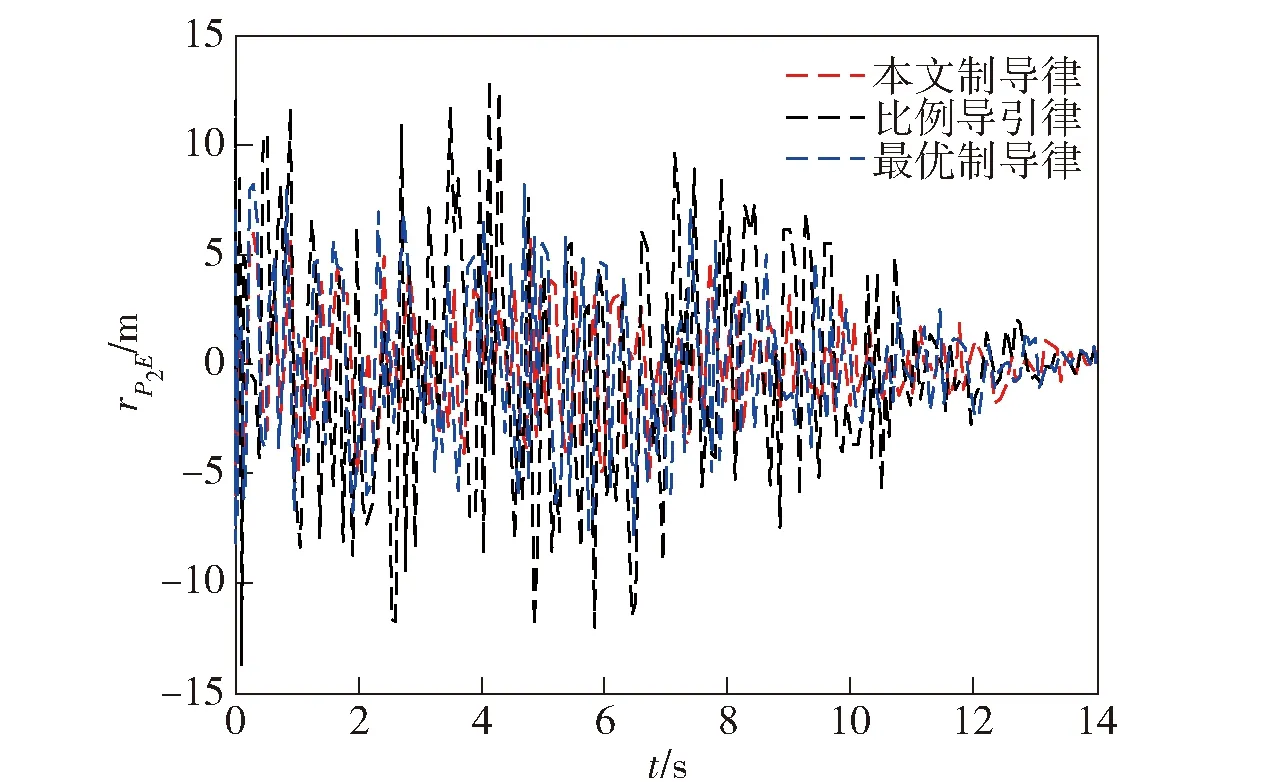
P(0) (15c) 则系统(12)式和(13)式关于(T,R,Q(t),S1,S2(t))有限时间有界且输入输出稳定。 证明1首先证明条件(15a)式~(15c)式能够保证系统有限时间有界。令V(x(t))=xT(t)P(t)x(t),则有 (16) 根据条件(15a)式和(16)式,可得 (17) (18) 根据(17)式和(18)式,可得 (19) 对(19)式积分,结合条件(15c)式,由 根据条件(15b)式,可得 2xT(t)Q(t)x(t) 因此,对于任意t∈[0,T],条件(15a)式~(15c)式可以保证系统(12)式和(13)式关于(T,R,Q(t),S1)有限时间有界。 同时,根据引理可知,(15a)式和(15b)式可以保证系统关于(T,S1,S2(t))有限时间输入输出稳定,因此定理得证。 由2.1节的基础知识可知,系统有限时间有界可用于描述系统状态对外界干扰的稳定能力,而系统有限时间输入输出稳定可用于描述系统输出对外界干扰的稳定能力。因此,有限时间有界和输入输出稳定理论可用于解决本文制导律有限时间收敛且过载受限问题。 (20) (21) 对于闭环系统(20)式和(21)式,为有效解算状态反馈矩阵K(t),可以采用状态反馈使系统同时满足有限时间有界且输入输出稳定。 定理2状态反馈控制器设计。在有限时间[0,T]内,如果存在X(t)∈Rn×n和L(t)∈Rr×n,使得(22a)式~(22c)式成立, (22a) X-1(t)≥S(t)且 (22b) X-1(0)>R, (22c) 则闭环系统(20)式和(21)式关于(T,R,Q(t),S1,S2(t))有限时间有界且输入输出稳定。此时,状态反馈矩阵可由K(t)=L(t)X-1(t)解算得到。其中,X(t)∈Rn×n和L(t)∈Rr×n均是对称正定的。 证明2根据(15a)式,由矩阵的Schur补性质[28]可知如下矩阵不等式成立: (23) (24) 同理,根据逆变相关知识,(15b)式和(15c)式等价于(22b)式和(22c)式,因此定理2得证。 在上述控制器解算过程中,通过调制状态修正量δ即可使飞行器在协同拦截过程中保持一定的视线分离角,进而增强协同探测效能。通过定理2解算的控制器能够使系统(20)式和(21)式同时满足有限时间有界且有限时间输入输出稳定,所设计的制导律能够同时保证视线分离角收敛到预置的值、视线角速率收敛到0 rad/s,且拦截器加速度不超过最大物理限制,从而在增强协同探测效能的同时保证拦截器实现有效拦截,因此1.4节提出的协同制导问题可由定理2解决。 基于第2节的协同拦截模型和协同制导律设计方法,本节开展仿真研究以检验所提方法的有效性。根据定理2所述方法解算控制输入u(t),将解算的协同制导律加入系统状态方程,进而得到制导系统状态和输出变化曲线。为较全面地检验所提制导律的性能,考虑目标飞行器进行常速运动和Weave机动两种情况。部分仿真参数如表1所示。 表1 仿真参数设置 假设目标以120 m/s常速运动,拦截情形为追击拦截,取δ=[0.524 -0.524 0 0 0 0 0]为状态变量修正量(即视线分离角φ设置为60°),仿真参数设置如表1所示。为比较本文方法与其他方法的优劣,在上述仿真条件下,2个拦截器分别采用本文制导方法、比例导引法以及文献[25]中的最优控制法(拦截角分别设置为-30°和30°),后文图例中分别用A、B、C表示本文制导方法、比例导引法、最优控制法。在协同制导的有限时间[0,tf]内开展仿真实验,所得结果如图2~图7所示。 图2 目标常速运动时飞行器协同拦截轨迹Fig.2 Interception trajectories of interceptors for a target moving at a constant speed 图3 视线分离角变化曲线Fig.3 Curves of line-of-sight separation angle 图4 加速度变化曲线Fig.4 Curves of acceleration 图5 视线角速率变化曲线Fig.5 Curves of line-of-sight angular rates 由图2和图3可知:当目标常速机动时,本文制导方法能够在协同制导的有限时间内有效规划拦截轨迹,克服初始视线分离角和视线角速率的不利影响,使拦截器保持一定的拦截构形,同时视线分离角始终保持较大的状态,并最终收敛到预定角度;而采用比例导引时,拦截器径直飞向目标,其飞行路径较为固定,不能在拦截过程中有效改变拦截构形,也不能有效调制拦截角;采用最优制导时,其构形较比例导引有所改善,视线分离角能够在一定程度上收敛到预置角度附近,但比例导引和最优制导不能保证视线角在有限时间收敛,其制导效果不如本文所提有限时间制导方法。 由图4可知,拦截器采用本文所提制导律时最大加速度为166 m/s2,表明本文所提制导方法能够在制导全程保证拦截器的需用加速度均不超过最大物理限制。图5所示视线角速率变化曲线表明,本文所提制导方法能够保证拦截器视线角速率最终收敛到0 rad/s,该性能能够保证拦截器在制导末段稳定视线角速率,进而取得较小的拦截脱靶量。 图6 协同探测误差变化(rP1E)Fig.6 Curves of cooperative detection error for rP1E 图7 协同探测误差变化(rP2E)Fig.7 Curves of cooperative detection error for rP2E 由图6和图7可知,本文所提制导方法与比例导引和最优制导相比,能够保持更好的构形,进而在制导全程有效增强协同探测效能、有效减小相对探测误差。 分析图2~图7可知:比例导引和最优制导方法不具备有限时间收敛特性,视线角不能在有限时间内收敛到预定值,在构形保持和探测环节均表现出明显的弊端;本文所提制导律能够同时保证视线分离角收敛到预置角度、视线角速率收敛到0 rad/s,且拦截器加速度不超过最大物理限制,在协同拦截过程中能够有效规划协同拦截轨迹,使拦截器在制导全程保持较大的视线分离角,进而降低协同探测误差,上述仿真结果验证了本文所提方法的有效性。 当目标进行更加剧烈的Weave机动时,假设目标加速度aEC=60sin(1.2t+π/2),其余参数设置与3.1节相同,其仿真结果如图8~图13所示。 图8 目标Weave机动时飞行器协同拦截轨迹Fig.8 Interception trajectories of interceptors for a target performing the Weave maneuver 图9 视线分离角变化曲线Fig.9 Curves of line-of-sight separation angle 由图8和图9可知,当目标飞行器进行更剧烈的Weave机动时,3种方法均能够保证拦截器有效拦截目标飞行器,三者的不同在于:本文所提方法能够有效规划和调制拦截轨迹,保持较好的探测构形;而且在目标进行大幅机动情况下也能有效调制视线分离角,使其保持在较大的状态,并最终收敛到预置角度;采用比例导引时,拦截器在制导指令作用下直接飞向目标,不能有效调制视线分离角;采用最优制导时,其视线角收敛效果较差,远不如目标进行匀速运动的情况。 图10所示的加速度变化曲线表明,在目标进行剧烈的Weave机动情况下,本文所提制导方法能够保证加速度不超过最大物理限制,并最终跟上目标机动。对比图5和图11可知:在目标进行剧烈运动时,本文所提制导方法仍能够确保视线角速率收敛到0 rad/s,实现稳定跟踪;采用比例导引和最优制导时,拦截器不能有效跟踪目标飞行器,视线角速率最终也不能收敛到0 rad/s,表明本文所提方法在有限时间内具有较强的鲁棒性和适应性。由图11可知,拦截器在有效拦截目标的同时其加速度亦不超过最大物理载荷,表明本文协同制导方法在拦截大幅机动目标时也具有较好的实用价值。 图10 加速度变化曲线Fig.10 Curves of acceleration 图11 视线角速率变化曲线Fig.11 Curves of line-of-sight angular rate 图12 协同探测误差变化(rP1E)Fig.12 Curves of cooperative detection error for rP1E 由图12和图13可知:在目标进行剧烈机动情况下,拦截器采用本文所提制导方法时,其相对距离协同探测误差稳定在6 m以内;而采用比例导引和最优制导时,其误差明显增大。 图13 协同探测误差变化(rP2E)Fig.13 Curves of cooperative detection error for rP2E 综上所述,在目标进行常速运动和较剧烈的Weave机动情况下,本文所提制导方法均能够保证拦截器在有限时间内以预置的分离角有效拦截目标,保证视线角速率收敛到0 rad/s且加速度不超过最大物理限制。而由于比例导引和最优制导律在有限时间内具有较大的保守性,其效果不如本文所提方法。 针对多飞行器协同拦截机动目标问题,本文在进行制导设计时充分考虑协同探测效能,基于有限时间控制理论提出了一种考虑探测构形的协同制导方法。所得主要结论如下: 1)基于相对运动方程、飞行器1阶动力学特性和协同探测原理,建立了协同拦截模型。 2)建模过程中将目标机动视为外界干扰输入,选取拦截器加速度指令为系统中间状态变量,以视线分离角和视线角速率变化为系统评价输出,基于系统有限时间有界和输入输出稳定定理设计了协同制导律。 3)本文所提设计方法可以同时保证系统评价输出有限时间稳定且中间状态不超过最大界限,能够在物理过载受限时有效增强协同探测和制导效果,仿真结果验证了所提方法的有效性。
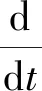
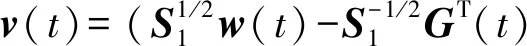
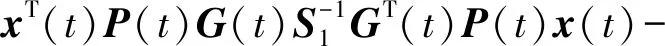
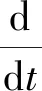
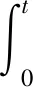
2.3 考虑探测构形的有限时间协同制导律

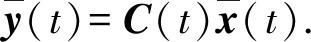
S(t)=max{2Q(t),CT(t)S2(t)C(t)},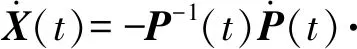
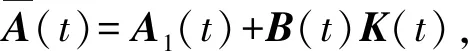
3 仿真分析

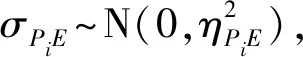
3.1 目标常速机动


3.2 目标Weave机动

4 结论

