申威众核处理器上的三对角并行求解器*

刘 侃，王欣亮，许 平，薛 巍,2+

1.清华大学 计算机科学与技术系，北京100086

2.国家超级计算无锡中心，江苏 无锡214100

+通讯作者E-mail:xuewei@mail.tsinghua.edu.cn

1 引言

计算机数值模拟是科学和工程领域广泛使用的研究方法。通过将真实的问题经过数学建模，可以用数值计算的方式对这些问题进行模拟。在计算机中，连续的真实世界往往用有限、离散的数据来表示。随着人们对数值模拟精度的需求越来越高，高分辨率的数值模拟成为必需。而高分辨率带来的大数据量和大计算量，则对数值计算的性能提出了非常高的要求。

偏微分方程是真实问题中常见的一类数学模型。对于含时的偏微分方程，主要的两种求解方法是显式方法和隐式方法。其中，隐式方法可以将微分方程的求解转化为一系列线性方程组的求解。而对于一维空间的问题，隐式方法中最常见的线性方程组便是三对角方程。而在二维和三维空间的问题的求解中，常有需要求解大量一维子问题的场景，如交替方向隐式方法[1-2]、迭代求解器的预调节器[3]等。因此，三对角方程求解器广泛地被应用于如计算机图形学[1,4-5]、流体力学[2,4,6]、三次样条计算[7]等众多科学和工程领域。为了解决实际应用中在高维空间中求解大量一维子问题的需要，本文所讨论的范围是求解大量的、规模不太大的三对角方程的情况，求解器最重要的性能指标是吞吐率，即大量三对角方程的总未知数数量与总求解时间之比。

目前，对于三对角方程，中央处理器（central processing unit，CPU）、图形处理器（graphics processing unit，GPU）等主流硬件平台上都提出了高度优化的并行算法，同时有基础数学库支持。但是对于申威26010众核处理器，还没有一种算法能有效地利用其硬件特性来达到最大化的性能。针对这一现状，本文综合考虑的申威处理器的硬件特性，从计算量、访存量和并行度等方面分析追赶法（Thomas algorithm）、循环消去（cyclic reduction，CR）算法和并行循环消去（parallel cyclic reduction，PCR）算法在申威处理器上可能达到的性能，设计了一种面向申威处理器的分布式CR 算法swDCR（Sunway-oriented distributive cyclic reduction）。其吞吐率相比主核上的追赶法达到了单精度43.9 倍和双精度36.7 倍的加速，相比从核上的追赶法达到了单精度和双精度均2.07倍的加速。

2 背景介绍

2.1 申威处理器架构介绍

申威26010 众核处理器是中国第一款自主研发的众核处理器。基于申威26010 处理器的神威太湖之光超级计算机，在2016 年到2017 年间曾是世界上计算能力最高的超级计算机，至2018 年11 月世界排名仍居第三。其理论计算能力达125 PFlops，Linpack[8]实测计算能力达到93 PFlops。

申威26010 众核处理器架构如图1 所示。一个处理器包含4个核组，每个核组具有765 GFlops的峰值计算能力和34.1 GB/s的理论访存带宽。每个核组包含一个主核（management processing element，MPE）和64 个从核（computation processing element，CPE），从核通过8×8网格的形式组织成从核阵列。

Fig.1 Architecture of Sunway 26010 many-core processor图1 申威26010 众核处理器架构

每个主核具有一个32 KB 一级指令缓存、一个32 KB 一级数据缓存和一个256 KB 二级缓存，每个从核具有一个16 KB 指令缓存和64 KB 便笺式存储器（scratch pad memory，SPM）。除了SPM 以外的缓存都是由硬件控制，并对软件透明的。SPM 的访问延迟和带宽与主核的一级缓存相当，但区别在于软件可控。

从核对主存的访问有两种模式：全局读入/写出（global load/store，gload/gstore）和直接内存访问（direct memory access，DMA）。gload/gstore完成主存和寄存器之间的数据传输，带宽较低，适合细粒度的数据访问；DMA 完成主存和SPM 缓存之间的数据传输，在访问大段连续数据时带宽较高，适合粗粒度的数据访问。根据Xu等的测试[9]，用一个核组64个从核运行Stream Triad测试程序，测得DMA的带宽为22.6 GB/s，而gload/gstore的带宽只有不到1.5 GB/s。

在从核组成的8×8阵列上，同行或同列的两个从核之间可以通过寄存器通信高速互传数据。每个从核具有一个寄存器发送缓冲区、一个寄存器行接收缓冲区和一个寄存器列接收缓冲区。在进行寄存器通信时，发送方从核会将数据放入发送缓冲区，并由核间互连将数据传输到接收方从核的行/列接收缓冲区中。在接收数据时，接收方从核会从行/列接收缓冲区取出数据。利用寄存器通信可以实现核间数据的高带宽低延迟传输，根据Xu等的测试[9]，两个从核之间的点到点通信延迟不超过11 个指令周期，单个核组的从核阵列上的寄存器通信集合带宽可以高达637 GB/s。寄存器通信没有低层缓存的访问开销，无论是延迟还是带宽，都远远优于目前主流硬件平台上通过共享缓存实现的核间通信。

申威处理器的寄存器通信机制存在来源混淆问题。当一个从核1可能要从同列的从核0和从核2接收数据时，来自从核0和从核2的数据都会被放入从核1的寄存器列接收缓冲区中，当从核1从寄存器列接收缓冲区中取数据时便不能区分其来源。在必要时，需要加同步使得两次寄存器通信先后进行，或将发送源的编号作为数据的一部分进行通信。

综上所述，在设计申威处理器上的算法时需要考虑三个硬件特性：

SPM 缓存：软件可控的特性使得它比硬件控制的缓存更灵活，但是需要考虑将哪些数据放入缓存中。

DMA：带宽远高于gload/gstore，但只适用于粗粒度的内存访问。应尽可能避免零散的数据访问。

寄存器通信：可以实现核间高速的数据传递，但只能在同行或同列间传输，而且应该避免来源混淆问题。

2.2 三对角方程求解算法的相关工作

三对角方程是一类形如Ax=d的方程组，其中A是三对角矩阵，d是已知向量，需要求解未知向量x，如图2（a）所示。在内存中，矩阵A的三条对角线和右端向量d通常是连续存储的，并且可以认为存在a0=cn-1=0，以保证数据对齐，如图2（b）所示。

Fig.2 Definition of tridiagonal equations图2 三对角方程的定义

三对角方程的经典解法是基于高斯消去法的追赶法[10]。追赶法分为前向分解和后向回代两个阶段，在前向分解中，通过式（1），从第一行到最后一行，将方程变为上三角形式。

在后向回代过程中，通过式（2），从最后一行到第一行，求出解。

如果不考虑向量化和缓存，那么追赶法的计算量和访存量都是最小的，因此是最快的串行算法。追赶法在求解单个三对角方程时是完全串行的，虽然在线程级粗粒度并行上，多个方程可以并行地求解，但是难以有效地利用向量化等细粒度并行机制。

CR算法由Hockney在1965年提出[11]。该算法包含两个阶段：前向消去阶段和后向回代阶段。在前向消去阶段，将方程的偶数行提取出，按照式（3）得到一个规模折半的方程。

对新的方程可递归地进行消去，直到得到一个两个未知数的方程时，可直接求解。

在后向回代阶段，当偶数行的解已被求出时，按照式（4）可求得奇数行的解。

CR 算法可就地进行，即用新的a、b、c和d覆盖内存中偶数行的a、b、c和d的位置。但这会使新的方程在内存中不连续，影响后续访问的效率。针对这个问题，Göddeke 和Strzodka 讨论了数据布局的优化和利用GPU 共享内存的优化[12]；Davidson 和Owens讨论了GPU上的寄存器打包的优化[13]。

在CR算法的基础上，Hockney 和Jesshope 于1981 年提出了PCR 算法[14]。与CR 算法不同之处在于，PCR算法不仅提取出原方程的偶数行做消去，也提取出原方程的奇数行做消去，从而将原方程转化为两个规模折半的方程。将两个新方程分别递归求解后便可得到全部解，不再需要后向回代。

但是这个版本的PCR 算法是不实用的，因为它的计算复杂度相比追赶法和CR 算法的O(n)提高到了O(nlgn)。为了解决这一问题，Sakharnykh 将它与追赶法结合提出PCR-并行追赶法（PCR-pThomas algorithm）[2,6]，将原来的lgn层递归分解改为常数层分解，之后并行地用追赶法求解所得到的常数个小规模的方程。这样使得访存和计算次数大幅减少，而且处理器的向量化运算仍然可以得到充分利用，但是多线程并行较困难。Kim等通过利用GPU上的共享内存进一步优化了内存访问，提出了tiled-PCRpThomas 算法，其访存量与经典的追赶法一致[15]。Wang 等通过将这一算法推广到英特尔至强融合架构，利用寄存器优化内存访问，并分析了PCR层数的最佳选择，提出了register-PCR-(half)-pThomas算法[16]。

另外，Bondeli[17]、Polizzi等[18]和Chang等[19]也分别从不同的角度讨论了大规模三对角方程的求解，但都是采用分治策略，将它的求解转化成很多小规模方程的求解。本文所讨论的范围是求解大量的、规模不太大的三对角方程的情况。

表1 总结了追赶法、CR 算法和PCR-pThomas 算法的优缺点。

Table 1 Comparison of Thomas,CR algorithm and PCR-pThomas algorithm表1 追赶法、CR算法和PCR-pThomas算法的比较

3 申威众核架构的三对角方程并行求解算法分析

首先考虑追赶法。在申威处理器的从核上，单精度除法的平均每条指令周期数（cycles per instruction，CPI）约为加乘的15倍；若将一次除法折合成15个加乘，则单精度下标量计算访存比为0.917。同理，双精度下将除法折合成30 次加乘，计算访存比则为0.875。因此在申威处理器的从核上，追赶法是访存受限的。

然后考虑PCR-pThomas 算法。一方面，申威处理器对单精度和双精度浮点运算的向量化宽度都只有4 个浮点数。如表2 所示，PCR-pThomas 算法中，最多只能相比追赶法减少0.5n次向量除法，同时还要引入额外的向量混洗（shuffle）操作，向量化给PCR-pThomas 算法带来的提升空间小。另一方面，PCR-pThomas 算法和追赶法的访存量相同，受到同样的访存带宽限制。综合以上两点，可以发现，PCRpThomas算法很难达到比追赶法更高的性能，因此在这两者之中选择更简单的追赶法即可。

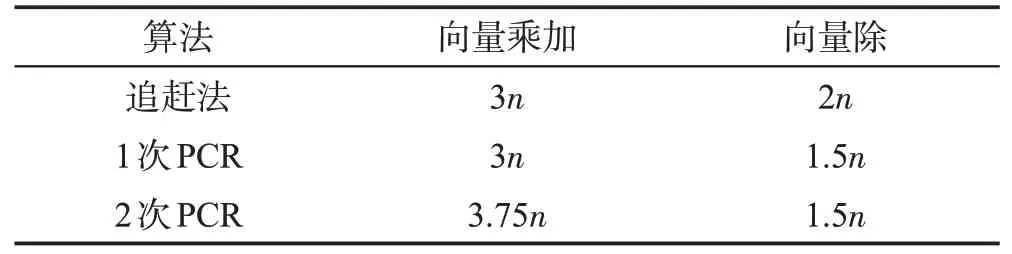
Table 2 Number of floating point operations in Thomas and PCR-pThomas algorithm表2 追赶法与PCR-pThomas算法的浮点运算次数

追赶法在申威处理器上是访存受限的，要想达到比追赶法更高的性能，必须减少访存量。在追赶法中，4/9的访存是读写中间变量，即前向消去之后的超对角线和右端向量。注意到申威处理器从核阵列上的缓存是软件可控的，如果能将这些中间变量放在高速缓存中，那么三对角方程求解器的性能相比追赶法仍有80%的提升空间。

然而每个从核上的缓存大小是有限的，要将所有中间变量都保存在缓存中，单个从核所能求解的方程规模是有上限的。单个从核的缓存是64 KB，考虑到其他栈变量需要占用一定的空间，可求解的方程规模上限在单精度为2 048维，在双精度下为1 024维；这样的规模上限对于实际问题来说限制太大。对于更大的规模就需要更大的缓存，为此可以将多个从核的缓存联合起来，也就是使用多个从核来求解一个方程。

由于涉及到多核，求解算法必须支持线程级并行，否则不同核之间只能串行执行，每个核都会把很多时间浪费在等待其他核上，使得效率较低。追赶法本身不能并行，而PCR-pThomas 算法为了减少计算量和访存量，舍弃了线程级并行的机会。因此，应该选择支持线程级并行的CR算法。

本文以CR算法为原型，设计了适合申威处理器的swDCR算法。通过联合最多64个从核，使得可求解的方程的规模上限提高到了单精度下131 072 维和双精度下65 536 维。同时，利用申威处理器的寄存器通信机制，使得CR算法的前后依赖数据能在不同从核间有效地传输。

4 swDCR的实现与优化

4.1 基础实现

使用从核缓存中的48 KB来存储中间数据，其中最初读入的原始方程占32 KB。在CR算法的每次前向消去时，将得到的新方程写到当前空闲的空间，同时将原方程的奇数行打包到原方程所占用空间的前半部分。在消去完成后，原方程所占空间的后半部分就被腾出用于下一层消去，整个过程的中间变量便可以存放在这48 KB中；同时打包也可使回代过程的数据访问变得连续，便于利用向量化运算。

经过一定次数的消去后，每个线程所处理的方程规模都不超过4，此时使用追赶法求解。由于此时数据仍然分布在各个从核的缓存中，称这一过程的算法为分布式追赶法。虽然它用到了多核，但是实际的执行仍然是串行的，不过由于方程规模足够小，这部分消耗的时间对整体性能影响很小。在追赶法的前向分解过程中，每个线程会等待前面的线程完成前向分解，并通过寄存器通信将前向消去之后的超对角线和右端向量的最后一个元素传过来。每个线程完成前向分解后会将该线程处理部分的超对角线和右端向量的最后一个元素传输给后方线程。而后向回代过程也是同样，先等待后方线程，再求解，然后将解的第一个元素传输给前方线程。

为了更高的吞吐率，解单个方程时所用到的从核数应该尽可能得少，同时每个从核所处理的问题规模不能超过其上限nmax。可以根据输入规模来选择单个方程所用的从核数，如式（5）所示。

若所得到的p大于64，即不可能把CR算法所有中间变量放入缓存中，而必须写入主存。当涉及到主存访问时，CR 算法访存量大的问题将极大地降低算法的效率。另外，大规模的三对角方程也不在本文讨论范围内。在这种情况下，由于追赶法的访存量更小，选择回退到追赶法。

4.2 向量化

申威架构下单精度和双精度浮点运算的向量化宽度都是4 个浮点数。为了有效地利用向量化来加速CR算法的消去与回代过程，应该使得每个线程处理的原方程行数是8的倍数，经消去后得到的新方程的行数是4 的倍数，以保证所有数据的对齐访问，并避免出现不能向量化的余数部分。虽然可以通过在方程前后补上单位矩阵来使得原始方程规模是8 的倍数，但是经过一次消去后得到的新方程的规模只有原始方程的一半，不一定仍是8的倍数。

针对这一问题，在swDCR算法每次消去之前，引入“借”的机制。在每次消去前，假设线程所处理的原方程的行数已经是8的倍数，那么在需要时该线程会从后方线程“借”方程的4行来自己处理，从而保证在每次消去时处理的方程行数都是8 的倍数。如果这个“借”的过程发生了，那么在回代之后，也需要将所得到的解“还”给后方线程。

在每一层消去时，每个线程将计算自己所处理的方程行数和起始行号。若起始行号不是8的倍数，则当前线程的前4 行归前方线程处理；若终止行号不是8 的倍数，则后方线程的前4 行归当前线程处理。另外，若从后方线程“借”了4 行，这4 行也会被打包到原方程所占空间的前半部分，在回代时还会访问到。

4.3 线程布局

无论是swDCR 算法的消去和回代过程，还是分布式追赶法的求解，都需要每个线程与其前后的线程进行通信。考虑到从核间寄存器通信只能同行或同列传输，线程在从核上的布局需要满足要求：每个线程的前一个线程和后一个线程都在其同行或同列的从核上。一种简单的线程布局如图3（a）所示，其中紫色的线连接需要相互通信的两个从核。

Fig.3 Thread layout on CPEs图3 从核上的线程布局

这样的线程布局会引起寄存器通信时的来源混淆问题。针对这个问题，在两次寄存器通信之间加同步当然也是一种解决方法，但是这样的同步开销其实是可以避免的。考虑到从同行接收和从同列接收分别经由的是行接收缓冲区和列接收缓冲区两个不同的缓冲区，可以设计一种线程布局，使得对于每一个线程，其前一个线程和后一个线程的其中一个在同行的从核上，另一个在同列的从核上。新的线程布局如图3（b）所示。

5 实验

5.1 性能测试

使用申威处理器的一个核组进行实验。一个核组具有765 GFlop/s 的峰值计算能力和34.1 GB/s 的理论访存带宽。实验会测试主核上的追赶法、从核上的追赶法以及不同优化前后的swDCR算法。每个算法会测试规模从128 维到32 768 维的足够量的三对角方程，且分别测试单精度和双精度的问题。每个数据都是在重复运行200 次后取运行时间的平均值，并以总未知数数量除以总时间计算吞吐率，以总访存量除以总时间计算访存带宽。

图4 展示了不同算法在申威26010 处理器单个核组上求解单精度和双精度三对角方程的吞吐率和带宽。根据实验结果，主核上的追赶法在单精度和双精度下都只能获得1 GB/s 的带宽，从而吞吐率较低。而从核上的追赶法基本可以获得21 GB/s 以上的带宽，但是和本文所提出的swDCR算法相比，由于访存量较多，吞吐率并不高，约为单精度下6.0×108未知数/s，双精度下3.0×108未知数/s。

Fig.4 Throughput and bandwidth of different tridiagonal solvers图4 不同的三对角求解算法吞吐率和带宽

而本文所提出的swDCR 算法，可以获得比追赶法更高的24 GB/s 带宽，是理论带宽的70%。同时更少访存量使得吞吐率进一步提高，在不同规模下平均达到单精度下1.23×109未知数/s，双精度下6.2×108未知数/s。

图5展示了不同的优化对swDCR算法产生的性能提升。可以发现，向量化对于swDCR 的性能非常关键。在没有向量化的版本中，和追赶法相比并无太大的吞吐率优势；而在加入向量化优化后，性能得到了显著的提升。在方程规模较小时，同步的影响较小；而在方程规模较大，也就是所用的从核数较多时，同步对性能的影响逐渐显现出来。

同时可以发现，性能曲线随着方程规模的上升，性能会有阶跃式的下降，断点在4 096、8 192、16 384等位置。这主要是因为，在选择单个方程所用从核数时，在这些位置从核数翻倍，每个从核所处理的问题规模有阶跃式的减小，从而导致性能阶跃式地降低。这一现象在未经各项优化的版本上最为明显，而经过各项优化后，算法变得越来越受访存带宽限制，这样的阶跃式下降也变得越来越不明显。同时也可以发现，当每个从核所处理的问题规模逐渐增大时，性能也逐渐提升。

与主核上的追赶法相比，swDCR 算法在单精度和双精度下分别可以获得43.9 倍和36.7 倍的加速。与从核上的追赶法相比，swDCR 算法在单精度和双精度下均可获得2.07倍的加速。这样的加速效果超出了单从访存角度考虑得到的1.8倍理论值，相比追赶法，CR 算法适合向量化这一优势能带来额外的加速效果。

5.2 精度测试

swDCR在实现中是完全保精度的。为了验证其求解精度，选取5 个16 384 维的三对角矩阵A，令精确解x的所有元素全为1，计算右端向量d=Ax，以此作为测试算例。用不同算法求解得到x′后，计算前向方均根误差（root mean square error，RMSE），如式（6）所示。

在申威处理器上测试了swDCR算法和从核上的追赶法，作为参考，在英特尔处理器Core i7上也测试了Math Kernel Library 中带主元选取的LU 分解法（lower-upper triangular decomposition）。

表3展示了不同算法的求解误差。可以发现，不同算法的误差受对角占优性、正定性和条件数的影响基本一致。而swDCR 在对角占优的情况下，误差和带主元选取的LU 分解法在同一个数量级。但在非对角占优的情况下有大于10 倍的误差，这主要是因为在CR算法中，对角线元素作为除数出现在前向消去和后向回代的公式中，如果其绝对值较小则会产生较大误差。

Fig.5 Performance improvement of different optimizations of swDCR图5 swDCR的不同优化所产生的性能提升

Table 3 RMSE of different algorithms表3 不同算法的方均根误差

6 结束语

本文通过分析追赶法、CR算法和PCR算法在申威26010处理器上的性能，设计了基于申威处理器的swDCR 算法。通过联合多个从核上的软件可控缓存，将过程中的所有中间变量保存在缓存中，从而减少了主存的访问，提高了算法的效率。通过利用向量化运算等方式，进一步优化算法的性能，使得该算法在访存量已经达到理论上最少的前提下能利用硬件理论带宽的70%。其吞吐率相比主核上的追赶法达到了单精度43.9 倍和双精度36.7 倍的加速，相比从核上的追赶法达到了单精度和双精度均2.07倍的加速。

swDCR算法可联合最多64个从核使得可求解的问题规模达到单精度下131 072维和双精度下65 536维。虽然所能处理的规模已经能满足绝大多数现有的实际应用的需求，但是仍然是有限的。在进一步工作中，算法的可扩展性将要被着重考虑。一方面，对于未来可能出现的更大规模应用，还需要对算法进行更多改进；另一方面，该算法能否在未来可能出现的架构相似的处理器上获得足够的性能，还有待研究。