丹尼尔式鱼道隔板形式变化对水力特性的影响研究
朱澄浩,李卫明,郭泽云,粟一帆,彭 湃
(三峡大学水利与环境学院,湖北宜昌443002)
0 引 言
鱼道是一种重要的鱼类保护措施,对于帮助鱼类在河流中自由洄游具有重要的意义。从水力学的角度来讲,鱼道是一种消减能量、降低流速的装置,而丹尼尔式鱼道则是消能效果最佳的鱼道类型之一[1]。标准丹尼尔式鱼道利用隔板阻挡水流,使水流与后续来流发生碰撞,从而达到消能和降低流速的目的。标准丹尼尔式鱼道过水断面是矩形和三角形的组合,由于三角形断面的水力半径小于矩形断面(面积相同的情况下),减少三角形断面过流,池室水位壅高,进而为喜好在表层水域活动的鱼类创造更适宜的水深环境[2],但这种设计使喜欢在底层水域活动的鱼类(特别是体形较大的鱼)从三角形断面通过时易被刮伤。
Mallen-Cooper等[3]通过放鱼试验对3种不同坡度8.3%(1∶12)、14.3%(1∶7)和20%(1∶5)的丹尼尔式鱼道供不同体长鱼类通过的潜能进行了调查,发现当鱼道的坡度为8.3%时可供所有体长范围(体长范围为45~350 mm)的鱼通过,上溯成功率高达88%,这一结果表明丹尼尔式鱼道也适合体形较小和游泳能力弱的鱼类上溯通过,并认为通过控制鱼道的设计参数(如坡度、长度、宽度和深宽比等)可以极大地扩展丹尼尔式鱼道的应用范围。随着研究地不断深入,国内外学者对鱼道设计参数对水力特性的影响研究取得了较大的进展。Katopodis等[4]通过试验较早地发现丹尼尔式鱼道中心剖面处的流速从鱼道底部至水面呈现由小增大的趋势,并分别就B/b与a/b(其中,B为槽身净宽;b为隔板过水断面净宽;a为隔板间距)的变化对鱼道水力特性的影响进行了评价。Rajaratnam等[5]通过物理模型试验对丹尼尔式鱼道180°转弯段内的水力特性进行了研究,指出在转弯段可以让水流顺利偏转。Katopodis等[6]通过物理模型试验对不同几何结构的丹尼尔式鱼道进行了研究,结果表明,从竖直方向上来看,丹尼尔式鱼道底板附近的流速较低,可让游泳能力较差的鱼通过,而自由水面附近的流速则较大,适合游泳能力较强的鱼使用。佟雪丰等[7]对丹尼尔式鱼道内的紊流特性进行试验研究,主要对两种水深平面上的流速分布、紊动能、紊动强度和雷诺切应力进行了分析。胡健[8]利用数值模拟的方法探讨了鱼道坡度(8%、10%、12%和14%)、隔板形式(拱形隔板与平面隔板)以及增设圆柱形障碍物分别对丹尼尔式鱼道内水力特性的影响。
综上所述,丹尼尔式鱼道隔板形式变化改变了池室内水力特性,适当改变鱼道设计结构尺寸或形式,鱼道内的水流流态更适合鱼类上溯。研究表明,影响鱼道过鱼效果的水力因素不仅包含流态和流速,紊流特性对鱼类上溯也有重要影响,而目前的许多研究仅用了流态和流速来表征鱼道的水力特性。基于此,本文用物理试验验证数值模拟方法的可行性,并运用数值模拟的方法对丹尼尔式鱼道隔板形式变化对鱼道内流速流态、紊动能的影响着重分析,为鱼道设计提供一定的参考。
1 研究方法
1.1 物理模型试验
依据NB/T 35054—2015《水电工程过鱼设施设计规范》建立了比尺为1∶1的丹尼尔式局部试验模型,见图1。鱼道模型全长18.8 m,槽身宽1 m,底坡坡度8.3%,相邻两隔板之间间距1.28 m,鱼道内设12个池室,隔板垂直于鱼道底板,隔板详细设计尺寸见图2。
试验鱼道上游端与稳水池相连,下游端设有可调节开度的尾门。在试验过程中,水流经过矩形薄壁堰后进入稳水池再流入鱼道,通过尾门控制下游水深,实际入流流量由矩形量水堰测得。为便于观察鱼道内的水流情况,该试验鱼道两侧的边墙采用有机玻璃制成。试验采用声学多普勒测速仪对鱼道内测点的流速进行测量,试验工况为进口流量0.2 m3/s,上游水深0.6 m,下游水深0.7 m。

图1 丹尼尔式鱼道水工模型
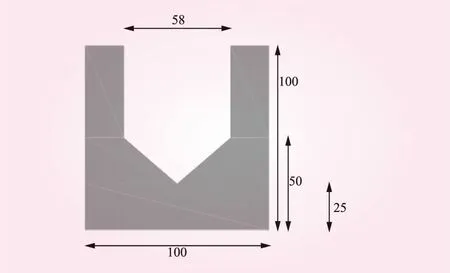
图2 隔板尺寸(单位:cm)
1.2 数学模型
数学模型建立:参照水工试验模型建立同尺寸的丹尼尔式鱼道数值模型,将顺水流方向定为x轴正方向,鱼道左岸方向为y轴正方向,重力反方向为z轴正方向确定坐标系,在模型中设置鱼道上游水体在x方向的范围为1.5 m,下游水体在x方向的范围为2.3 m,以基座底边和鱼道边墙最高点作为网格块轮廓线在z方向的上、下限,进行全流场精细模拟。
网格划分:模型性质设为固体,单位为SI制,模型设一个网格块,自动划分网格,设定合适网格总数使网格单元在各方向上的尺寸保持在0.02 m左右。
边界条件与初始条件:模型进出口边界条件设为压力边界,根据水工模型试验条件设置相应进口水深为0.6 m,出口水深为0.7 m。鱼道两侧的边墙及鱼道底部选择固壁边界,鱼道顶部设压力边界,流体分数设为0。初始条件设置限定鱼道上下游水体的范围,根据计算区域可确定上下游水体在x、y方向的范围,上下游水体的深度根据鱼道进出口压力边界条件确定,分别为0.6 m和0.7 m。
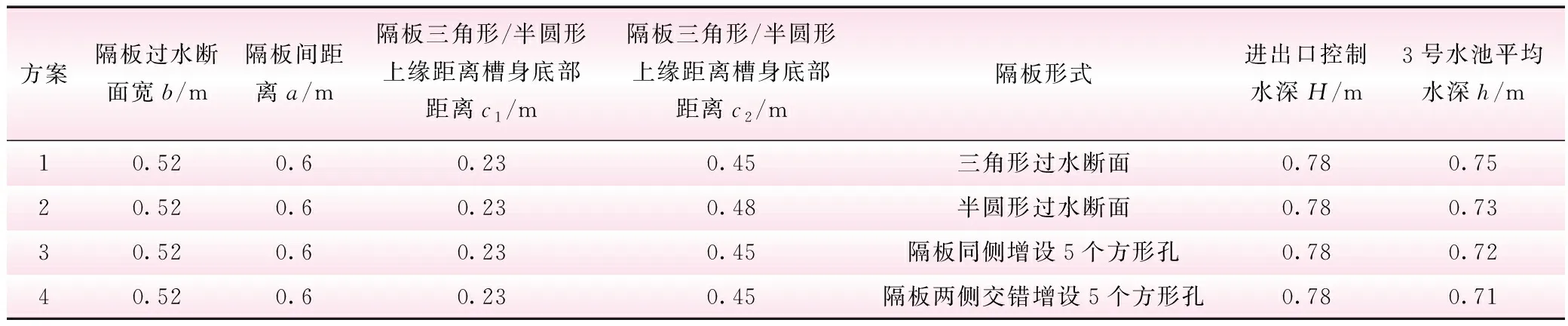
表1 不同隔板型式模拟方案
1.3 模型验证
(1)流速验证。进出口水流由于受到稳流池和尾门的影响,极不稳定,为了降低试验误差和减小池室两边挡板的影响,选取试验模型6号水池中央断面表层12个测点进行流速校核,相邻测点的间距为10 cm。6号水池中央断面表层流速的计算值与实测值结果对比如图3所示。由图3可知,测点流速值大于0.6 m/s,此流速范围是鱼类上溯主要集中的区域,因此某一处测点流速略有偏差不影响模型的结果。
(2)水深验证。鱼道1~12号水池内平均水深的计算值与实测值如图4所示。由图4可知,6号水池的水深测量断面水深对比分析满足要求,因此此数值模拟方法可以采用。
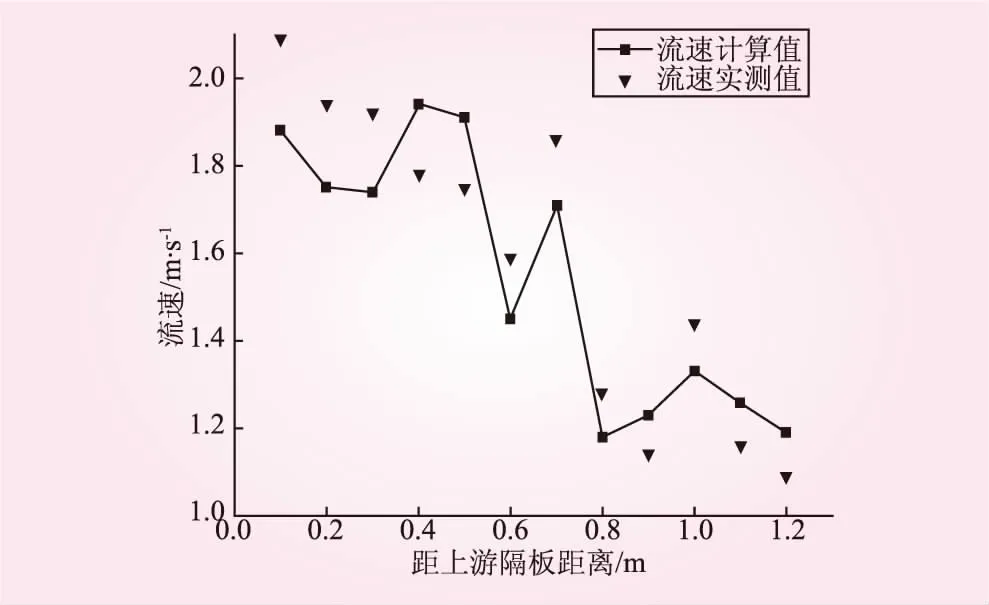
图3 6号池室表层流速计算值与实测值
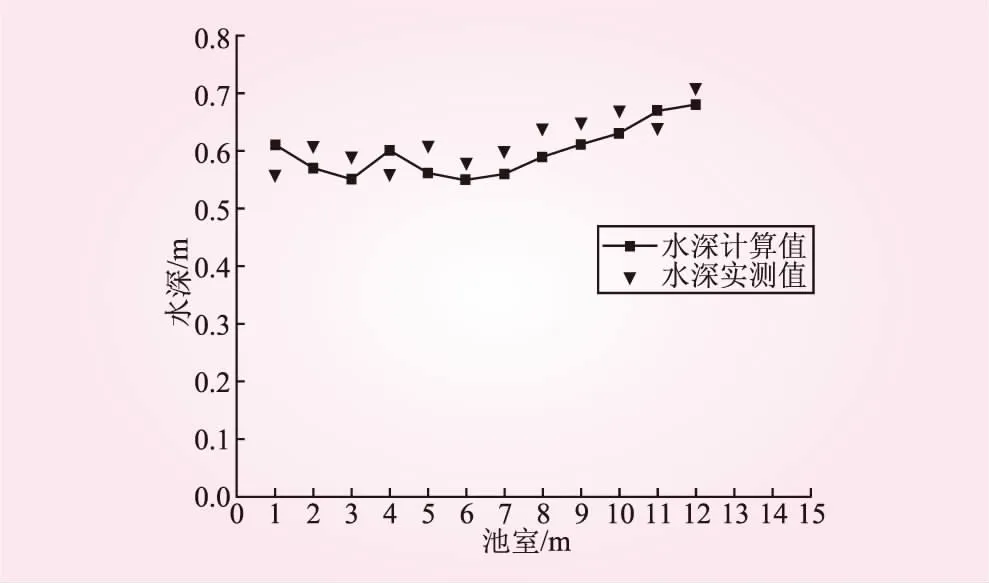
图4 鱼道内水深计算值与实测值
1.4 不同隔板形式数值模拟
模型试验结果证明了数值模型方法是可行的。为了研究不同隔板形式对水力特性的影响,模拟了4组不同隔板形式的丹尼尔鱼道模型,鱼道内部设5个池室,底坡坡度为1∶10,隔板与鱼道底板夹角为45°,不同隔板形式的相关参数见表1,隔板细部构造如图5所示。
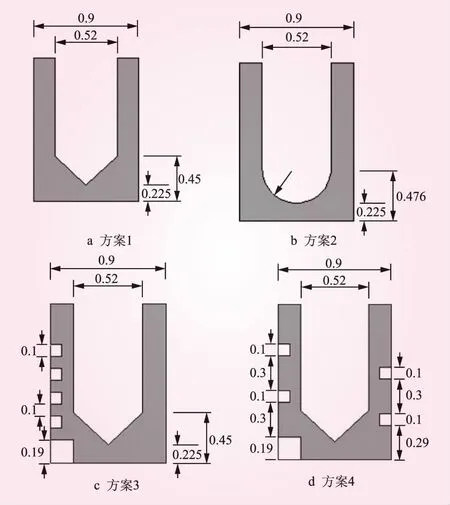
图5 不同隔板细部(单位:m)
2 结果与分析
2.1 隔板形式对流速分布的影响
以3号池室为例,对鱼道内的水力特性进行研究;选取0.25h、0.5h、0.75h3个水深层对水池内的水力特性进行分析。对丹尼尔式鱼道水力特性及鱼类行为研究表明,丹尼尔式鱼道内主流区的水流流速要大于鱼类感应流速,要使鱼类顺利上溯,鱼道设计流速(隔板过水断面上的最大流速值)应小于目标鱼类的突进游泳速度,水池中(不含隔板过水断面)的水流流速小于目标鱼类的临界游泳速度[9- 10]。研究不同隔板形式对池室流速分布的影响,为评价鱼类上溯有效性提供参考。
方案1流速数值模拟结果见图6,由方案1流速图可以看出,表层平均流速为1.31 m/s,大部分区域为高流速区,但过水断面处流速较小;中层平均流速为1.34 m/s,绝大部分区域为高流速区,约占该层的92%;底层水体平均流速为0.85 m/s,水流流速变化明显,最小的流速接近0。由于过水断面由矩形变为三角形,隔板附近流速均大于1.40 m/s,最大流速达到了2.28 m/s。
表层水流流经三角形过水断面后,靠近两侧挡板的水流向挡板两侧扩散,扩散至池室中间时受两侧边墙约束而向中间偏转,而过水断面中间水流呈“波浪纹形”向前,这主要是因为在隔板过水断面处生成的跌流扰乱了池室中间部位水流的平顺性;在中层水流流经隔板后向两侧扩散现象减弱,过水断面中间水流以更明显“波浪纹形”流向下一隔板,较表层水流流态更复杂;底层水流受隔板阻挡部分水体不再流动,但两侧的水流由于惯性与隔板发生碰撞,并在隔板与边墙所组成的直角三角形区域里形成回流区,回流区的流速大小在0.40~1.30 m/s之间。与方案1相比,方案2将隔板的过水断面由三角形断面改为半圆形断面,其底层流态特征与方案1中底层的水流形态相似,但相比于方案1,方案2中3号水池表、中、底层上的平均流速均增大,其中底层上低流速(小于1.00 m/s)区的相对面积较方案1减小了近15%,这主要是因为在相同面积情况下,半圆形的水力半径要大于三角形,而导致过流能力增大。
对比方案1、3中3号水池内不同水深层的流速分布,在隔板一侧设孔口,方案1、3的表层水流平均流速大小相差不大,但方案3流态明显好于方案1;方案3中层水流平均流速比方案1水流平均流速小0.34 m/s,底层水流平均流速较方案1小0.09 m/s,过水断面上的流速从表层至底层逐层减小,这说明方案3的布孔方式对隔板过水断面上流速的重新分布起到了积极作用。与方案1相比,方案3中流速分布更加合理。因此,在隔板一侧增设孔口改善了池室和过水断面的流速分布。
对比方案3、4中3号水池内不同水深层的流速分布,方案4的两侧交错布孔对过水断面流速的重新分布也起到了积极作用,布孔方式的变化对隔板过水断面上的平均流速没有影响,但与方案3相比,方案4底层上回流区的面积比方案3大。
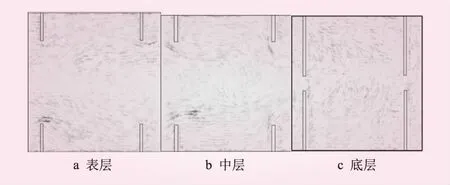
图6 方案1不同分析层流速云图
2.2 隔板形式对紊动能影响
紊流对鱼类游泳能力或行为的影响方面,国外研究人员作了较多的研究。Enders等[11]指出紊流可能会导致大西洋鲑(Salmo Salar)幼鱼在游泳时的体能消耗增大。Silva[12]等通过试验发现雷诺切应力是影响伊比利亚鲃(Luciobarbusbocagei)上溯的最关键因素之一。此外还发现鱼类在上溯过程中更喜欢经过紊动能低的区域,并将紊动能高、低的临界点确定为0.05 J /kg 。Alexandre[13]等利用肌动电流图遥测技术对伊比利亚鲃在淹没孔口式鱼道内的游泳行为进行研究,发现雷诺应力的水平分量与其游泳速度有着最为紧密的联系。Delavan等[14]对银侧美洲鱥(Notropisatherinoides)上溯途经水域的水力特性进行实地测量,发现当这片水域的水流流速介于银侧美洲鱥的临界游泳速度和爆发游泳速度之间并伴随有复杂的紊流时,银侧美洲鱥无法通过该水流障碍。由此可知,在复杂紊乱的水流中,由于鱼类受力的复杂性及运动阻力的增大,鱼类克服流速的能力将会减弱。谭均军等[15]发现鳙鱼和草鱼在上溯过程中会主动避开高紊动能区。因此,水流的紊动特性与鱼类的游泳能力及游泳行为密切相关,即水流的紊动程度越大,对鱼类游泳能力的抑制则越明显。
由数值模拟结果得,3号水池内方案1的表、中、底层的紊动能平均值分别为0.06、0.05、0.03 J/kg,沿水深方向逐渐减小,各水深层大部分区域的紊动能小于平均值,高紊动能区域分布范围很小,且基本在隔板附近和贴近边墙,其中底层紊动能最大值达到0.58 J/kg。与方案1相比,方案2表、中、底层上紊动能的平均值基本相同,紊动能大小范围均为0.02~0.06 J/kg,且分布位置也大致相同。因此,将隔板底部的三角形断面改为半圆形断面对水池内紊动能的影响较小。与方案1相比,方案3表层紊动能分布位置有所改变,池室内不同水深层紊动能平均值比方案1均偏大,中、底层紊动能分布区域大致相同,而表层有所不同,这说明增加的布孔重新改变了表层水流流向和流速,使水流流态更复杂,紊动能随之变大。对比方案3、4中3号水池内不同水深层紊动能可知,方案4紊动能分布情况与方案3大致相同,说明将孔口布置在隔板左侧还是右侧对紊动能分布无影响。
3 结 论
本文通过改变丹尼尔式隔板形式,分析了不同隔板形式对鱼道内水力特性的影响,得出如下结论:
(1)将隔板中三角形断面改为半圆形断面后,水池内的各水深层流态基本不变,但表层和底层的平均流速则分别增大9%和15%,且底层上小于1.00 m/s流速的区域的相对面积减小近15%,这对喜好在上层和底层生活的洄游鱼类是不利的,尤其是底栖型洄游鱼类;但半圆形过水断面隔板形式能有效降低鱼类上溯过程中可能遭受的物理伤害,满足鱼类上溯流速条件时也可考虑采用。
(2)在隔板同侧增设5个方形孔后,改善了水池表层和中层的流态,对底层流态影响不大,同时中层和底层的平均流速均有所减小,分别减小25%和11%;中层上小于1.00 m/s流速的区域相对面积增大约37%,这表明在隔板同侧增设孔口改善了池室水力特性。而在丹尼尔式鱼道隔板两侧交错布置方形孔与在隔板同侧布置方形孔池室水力特性基本相同,对紊动能的分布也影响不大,但底层回流区面积增大,有可能使鱼迷失方向。

