GNSS精密轨道产品不连续性分析及评估∗

董志华 陈俊平 周旭华

(1 中国科学院上海天文台 上海 200030)

(2 中国科学院大学 北京 100049)

1 引言

国际GNSS (Global Navigation Satellite System)服务(IGS)[1]旨在为导航定位用户提供高精度GNSS数据、产品和服务[2],其产品精度、一致性与连续性是高精度定位和导航的基础和前提.按照目前的国际规范,高精度GNSS轨道产品一般以天为周期进行发布,提供给用户使用,但连续多天的产品存在不同天之间的跳变问题.精密产品的跳变,将造成用户精密位置计算的不精确,从而影响针对地震监测、海平面变化等毫米级位置精度需求的应用.此外,由于IGS各个分析中心(Analysis Centers,AC)采用的数据处理策略和力学模型不同,其产品连续性也存在一定差异.Griffiths等人于2009年首次提出日边界不连续性(Day Boundary Discontinuities,DBD)分析法[3]进行轨道性能分析,之后许多学者也采用DBD进行GNSS精密产品精度的评定[4–7].DBD产生的原因在于动力学模型不完善等引起的轨道确定和预报的误差.因此,通过分析DBD的长期序列,能够评估目前GNSS轨道的精度情况,并能由其特性分析研究轨道确定过程中存在的误差.论文利用德国地学研究中心(GFZ)、欧洲定轨中心(COD)、欧空局(ESA)、美国喷气试验室(JPL)以及上海天文台(SHA)[8–9]5个GNSS分析中心2013—2017年的轨道产品,分析了轨道跳变的特性,发现跳变序列存在显著的周期项,并验证了地球反照辐射压和太阳光压模型等动力学模型对轨道的影响.

2 轨道连续性分析

2.1 轨道日边界不连续

DBD是连续两天的精密星历轨道在某一相同历元的3维坐标差异.A、B两天相同历元轨道在径向(R)、切向(T)和法向(N) 3个方向上的DBD,PDR、PDT、PDN可分别表示为:

其中, RA、TA、NA和RB、TB、NB分别是A、B两天的坐标.

目前国际各GNSS分析中心提供的单天精密卫星轨道产品所给的卫星坐标范围为00:00:00—23:45:00,两天数据间没有重叠时段,DBD的计算需要将第1天(Day A)的轨道外推一个历元至下一天(Day B)的零点,并与下一天SP3文件的零点轨道作差.

在利用图1所示方案进行DBD分析时,需要将轨道外推15 min.轨道外推采用的方法为轨道动力学拟合及外推.具体分析方法为: (1)利用精密星历数据中起点Tb至终点Te的精密轨道数据,进行精密轨道动力学拟合; (2)根据轨道拟合得到的卫星初始轨道根数以及太阳光压等动力学参数,利用轨道积分获取指定弧段的卫星轨道.

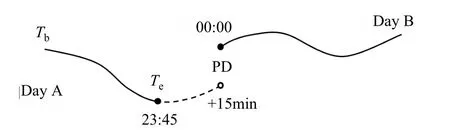
图1 轨道DBD的示意图,PD代表A、B连续两天SP3文件的差值, Tb代表起始时刻, Te代表终止时刻.Fig.1 Illustration of the day boundary discontinuity in the satellite orbits,PD is the position difference between A and B successive SP3 daily files, Tb is the beginning time, Te is the end time.

2.2 精度评估方法

本文采用均方根(root mean square,RMS)误差作为每颗卫星DBD评估的指标来分析与评估精密轨道产品的不连续性,对卫星s,其公式为

式中, m为误差分析的数据总天数; xs为第i天该GNSS卫星精密轨道产品的真值;为第i天该卫星精密轨道的外推值或拟合值.对于轨道外推和轨道不连续性,上述公式即其m天内卫星s的误差值; 对于轨道拟合,先用上述公式计算出1 d内每颗卫星轨道拟合的RMS值,再根据上述公式计算每颗卫星在m天内的RMS值.

3 数据分析

3.1 轨道外推精度分析

轨道外推的精度将影响DBD评估,首先进行轨道外推精度的分析.在以上轨道外推策略中,取Tb为A天00:00:00, Te为A天23:30:00,利用轨道外推方法获取A天23:45:00时刻的卫星轨道,并将该时刻的外推轨道与精密轨道的真实3维坐标进行比较,得到两者差值.使用BERNESE 5.2软件[10]进行轨道外推处理,轨道积分采用的策略如表1所示.

表1 轨道积分策略Table 1 The strategy of orbits integration

采用GFZ、COD、ESA、SHA和JPL 5个分析中心2013—2017年5 yr的精密轨道,进行轨道外推,分析所有卫星的外推精度情况.表2列出了所有GPS/GLONASS (GLOBAL NAVIGATION SATELLITE SYSTEM)卫星轨道外推3维坐标误差5 yr的统计的平均值,表中,JPL只提供GPS的精密轨道,Exp (Extrapolation)为轨道外推精度,Fit为轨道拟合精度.

由表2可以看出,各个分析中心的3维轨道拟合精度平均为2.6 mm; 其中GFZ最大,为2.93 mm; COD最小,为2.28 mm; SHA和JPL相当,分别为2.65 mm和2.63 mm;ESA为2.44 mm.轨道外推精度平均为4.6 mm,其中JPL最大,为6.04 mm; ESA最小,为3.20 mm; GFZ、COD和SHA依次为5.62 mm、3.71 mm和4.49 mm.轨道拟合和轨道外推的平均精度都小于5 mm,相比轨道拟合,轨道外推增加了大约2 mm的预报误差.

表2 各GNSS分析中心外推轨道3维误差(单位: 毫米)Table 2 Three-dimensional error of the orbits extrapolation of different GNSS analysis centers (unit: mm)

3.2 轨道日边界不连续性分析

以上分析表明,轨道15 min的预报误差平均为4.6 mm.进一步分析GNSS轨道日边界不连续性,根据图1所示方案,取Tb为A天00:00:00, Te为A天23:45:00,利用轨道外推方法获取该天24:00:00时刻的卫星轨道,并将外推获取的24:00:00时刻轨道与B天00:00:00时刻精密轨道的真实3维坐标进行比较,得到两者差值.利用该方法,对GFZ、COD、ESA、JPL以及SHA 5个分析中心2013—2017年5 yr的数据进行DBD分析.部分GPS/GLONASS卫星5 yr DBD值序列的RMS情况如图2–4所示.

图2 GPS/GLONASS卫星轨道径向跳变值的RMS值Fig.2 RMS values of the GPS/GLONASS satellites’ radial orbit jump

由图2–4可以看出,各个分析中心的轨道跳变均在厘米量级,远大于表2所统计出的平均为4.6 mm的轨道拟合和轨道外推残差,所以轨道拟合和外推对于分析轨道不连续性带来的误差可以忽略不计.对所有GPS卫星轨道跳变进行统计,各个分析中心R、T、N 3个方向的轨道跳变RMS平均值分别如下: GFZ为2.2 cm、2.7 cm、2.7 cm,ESA为2.1 cm、2.5 cm、2.1 cm,COD为0.7 cm、0.8 cm、0.7 cm,SHA为3.1 cm、4.5 cm、3.9 cm,JPL为1.5 cm、1.3 cm、1.5 cm.对所有GLONASS卫星轨道跳变进行统计,各个分析中心R、T、N 3个方向的轨道跳变RMS平均值分别如下: GFZ为5.3 cm、7.6 cm、5.9 cm,ESA为2.5 cm、9.1 cm、6.8 cm,COD为0.7 cm、1 cm、1.2 cm,SHA为7.9 cm、11.9 cm、8.7 cm.以上差异表明各GNSS分析中心在数据处理及软件策略方面仍存在一定差异.此外,径向轨道跳变量小于其他两个方向,这与轨道径向精度高于其他两个方向的情况一致.

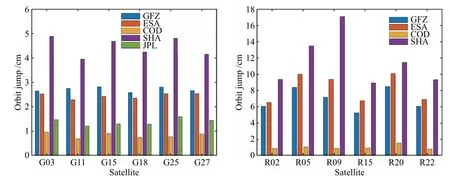
图3 GPS/GLONASS卫星轨道切向跳变值的RMS值Fig.3 RMS values of the GPS/GLONASS satellites’ tangential orbit jump

图4 GPS/GLONASS卫星轨道法向跳变值的RMS值Fig.4 RMS values of the GPS/GLONASS satellites’ normal orbit jump

将5个分析中心各颗卫星的3维轨道DBD进行RMS统计,如表3所示.对于GPS卫星轨道3维跳变值的RMS统计,GFZ为4.48 cm、ESA为3.90 cm、COD为1.27 cm、SHA为6.77 cm、JPL为2.51 cm.对于GLONASS卫星轨道跳变值的RMS统计,GFZ为11.11 cm、ESA为11.63 cm、COD为1.74 cm、SHA为16.72 cm.COD在生成精密轨道产品采用的软件为本文使用的BERNESE软件,这可能是COD的DBD最小的原因之一.这也表明目前国际上各GNSS分析中心在数据处理上还存在模型的差异.此外,GLONASS卫星的轨道跳变均大于GPS卫星,这与目前GLONASS卫星精密产品精度相对较低一致.

表3 GPS/GLONASS卫星轨道3维跳变值的平均RMS值(单位: 厘米)Table 3 Mean RMS values of the GPS/GLONASS satellites’ three-dimensional orbit jump (unit: cm)

图5为COD、GFZ分析中心G29和G05卫星2013—2017年5 yr的轨道跳变序列,其中STDR、STDT、STDN分别为R、T、N 3个方向轨道跳变的标准差(STD),RMSR、RMST、RMSN分别为R、T、N 3个方向轨道跳变的均方根.从中可以看出,两个分析中心的轨道跳变在各个分量方向上均存在明显的周期特性.采用最小二乘频谱分析(least square spectrum analysis,LSSA)对轨道跳变的周期特性进行分析,并在频谱图峰值附近搜索主要周期[12].图6给出了GFZ分析中心G29卫星和COD分析中心G05卫星精密轨道在R、T、N 3个分量上跳变的频谱图.从图6可以看出,较显著的周期约为90 d、120 d、175 d、340 d、352 d; 其中90 d、120 d和340 d的周期项对应海潮对地球自转的影响,其振幅为数毫米至1 cm左右,表明轨道确定中的潮汐改正模型需进一步改进; 而175 d和352 d则是与卫星星座相关的1/2和1个交点年周期项[13–14].对其他卫星分析,都存在与这两颗星相近的周期特性.

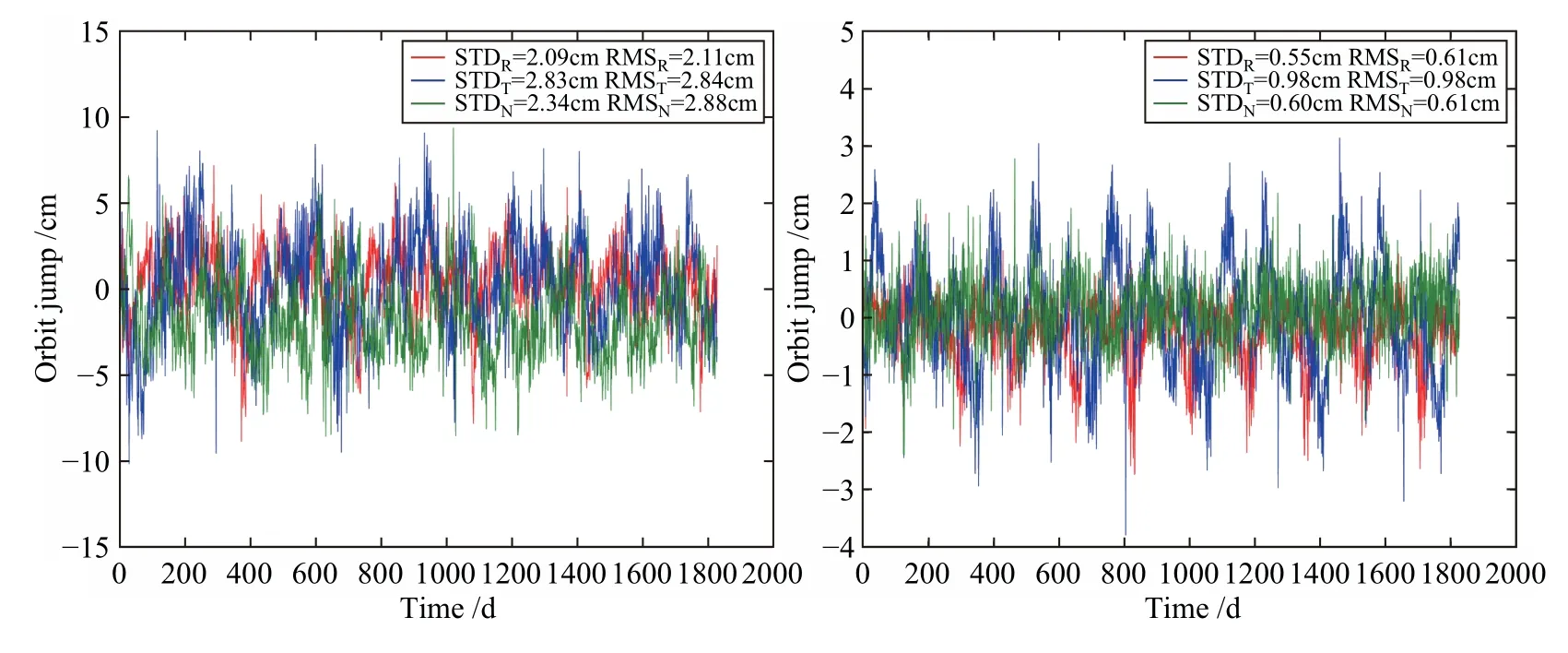
图5 GFZ/COD精密产品卫星G29 (左),G05 (右)轨道跳变Fig.5 The orbit jump in GFZ/COD precise products of satellites G29 (left),G05 (right)

图6 GFZ/COD精密产品卫星G29 (左),G05 (右)轨道跳变频谱分析Fig.6 The spectrum of the orbit jump in GFZ/COD precise products of satellites G29 (left),G05 (right)

4 力学模型对轨道外推精度的影响

分析DBD时采用的数据段2013—2017年5 yr,在此期间COD分析中心发生了两次比较大的力学模型的更新,分别是2013年7月14日(年积日195 d)地球反照辐射模型[15]的引入以及2015年1月4日(年积日4 d)太阳光压模型[16]的改变.其中,地球反照辐射是指太阳光照射至地表后部分反射回卫星处对卫星所引起的摄动.而导航卫星的太阳光压力是对轨道影响最大的非保守力,本文选取的数据时间段2013—2017年期间,COD采用的光压模型从2015年1月4日开始由ECOM1 (reduced ECOM)变更为ECOM2 (extended ECOM)[16–17].其中,ECOM1模型[17–18]为:

式中, D0、Y0、B0、B1,C和B1,S代表ECOM1模型的5个光压参数, u代表卫星在轨道平面上距升交点的角度.ECOM2模型[11,18]为:

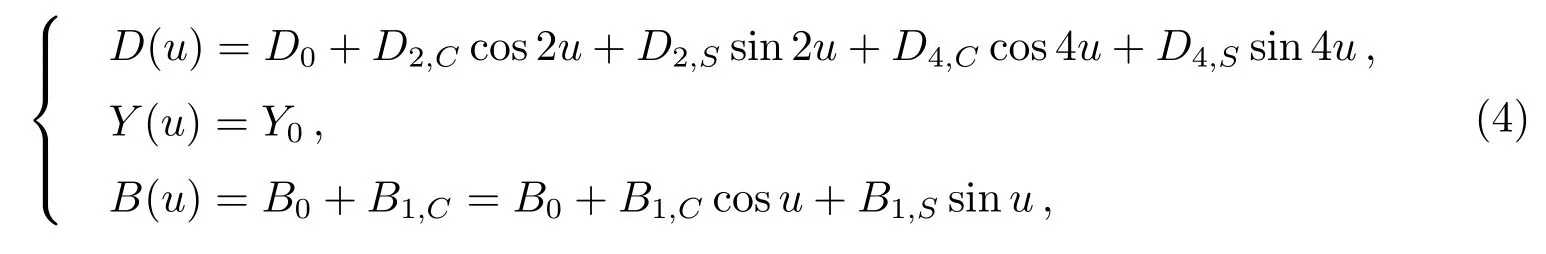
式中, D2,C、D2,S、D4,C和D4,S代表ECOM2模型中相较ECOM1模型多出的4个光压参数.两种光压模型的光压参数分别如表4所示.

表4 光压模型及参数[16−17]Table 4 Solar radiation pressure model and parameters[16−17]

可以看到ECOM2模型在ECOM1的基础上引入了包含2u和4u的周期项.为分析以上力学模型更新对轨道跳变分析的影响,对COD分析中心精密轨道的拟合和预报进行进一步分析.将表1中的太阳光压模型变为ECOM1重新进行轨道拟合及预报,重新分析COD中心2013—2017年轨道外推精度; 并与上述ECOM2模型的结果进行对比,结果如图7–8所示.

图7 COD分析中心G07卫星轨道外推精度,左图采用ECOM1,右图采用ECOM2.Fig.7 The precision of the orbits extrapolation of G07 satellite using ECOM1 (left) and ECOM2 (right)models.

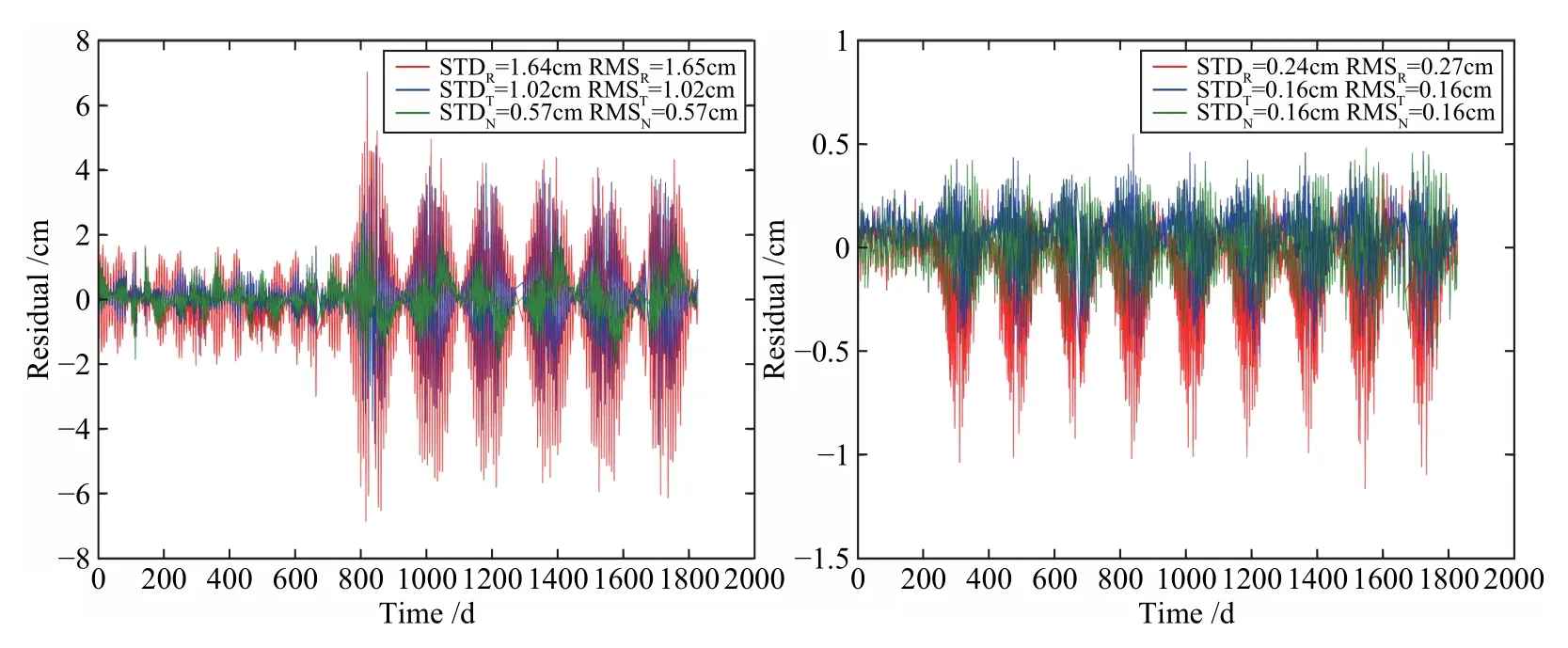
图8 COD分析中心R07卫星轨道外推精度,左图采用ECOM1,右图采用ECOM2.Fig.8 The precision of the orbits extrapolation of R07 satellite using ECOM1 (left) and ECOM2 (right)models.

图7和图8结果表明,采用ECOM1光压模型时,COD分析中心GPS/GLONASS卫星的外推轨道从第734日(即2015年1月4日)精度急剧降低,这与COD更新太阳光压模型的日期一致; 表明太阳光压模型的不一致,将使轨道外推精度劣化至厘米级.采用ECOM2光压模型时,COD分析中心GPS/GLONASS卫星的外推轨道在第195日,即2013年第195日精度迅速下降,这与COD引入地球反照辐射压的日期一致; 这表明,地球反照辐射压摄动同样会造成轨道外推的恶化; 并且可以看出卫星径向轨道存在系统偏差,表明地球反照辐射会引起GPS卫星径向轨道误差[15].

以上对比说明,地球反照辐射压、太阳光压模型等的差异会对轨道连续性产生较大影响.对ECOM1模型下G07卫星第734日后的3维外推轨道误差进行频谱分析,结果如图9所示.可以看到,光压模型的不一致,将为外推轨道引入1/4个交点年(即87 d左右)的周期误差,这与(3)–(4)式中4u项的周期一致; 而公式中2u项对轨道的影响不够显著,表明该项对轨道的影响有限.

图9 COD分析中心G07卫星外推轨道误差的频谱分析Fig.9 The spectrum of the 3D orbits extrapolation of G07 satellite

5 结论

本文计算了GFZ、COD、ESA、SHA和JPL这5个分析中心在2013—2017年5 yr间精密轨道产品天与天交界处的跳变,分析了其产品的连续性.计算结果表明:GFZ、COD、ESA、SHA和JPL的平均3维轨道跳变分别为7.79 cm、1.51 cm、7.77 cm、11.75 cm和2.51 cm,这些差异说明目前国际上各分析中心对这两个系统卫星的数据处理模型还存在一定的差异; 在此基础上,并对连续5 yr的轨道跳变序列进行最小二乘频谱分析,发现了与潮汐改正模型周期相近的周期为90 d、120 d、340 d左右的显著周期项误差,表明潮汐模型可能是影响GNSS轨道确定精度的因素; 此外,GPS轨道跳变序列呈现出与卫星星座相关的175 d和352 d左右的交点年显著周期项; 而地球反照辐射压和太阳光压模型等动力学模型不一致,也会引起轨道外推精度的下降,为外推轨道引入1/4个交点年(即87 d左右)的周期误差; 地球反照辐射压摄动还将引起卫星径向轨道的误差.