CRH5动车组车体底架的结构分析与轻量化研究
元艳玲,樊祺超,李汝楠,杜芮琪
(太原科技大学交通与物流学院,太原 030024)
20世纪60年代,Schmit[1]提出系统综合的概念,标志着结构优化思想的诞生和形成。在保证车体结构安全的前提下,对车体结构进行分析并进行轻量化设计是当前的研究热点。轻量化研究主要有三个方向:一是改变列车使用材料;二是使用新工艺[2];三是改变列车结构,从源头设计出发,通过对结构的优化设计来减轻车重[3]。前二者效果显著但成本过高。本文拟通过结构优化的方法探索轻量化途径,以CRH5动车组的M2S车体底架为对象,采用基于连续变量和离散变量的尺寸优化对比验证的方法,探索有效的轻量化途径。
刘丹丹等[4]基于尺寸优化理论,对城市客车车身模型选用SHELL单元进行网格划分,并选取工况对有限元模型进行优化,使得车身质量下降了22.81 kg.周文[5]对某运输车车架进行形状优化,在网格优化时使用变形区与控制炳的方法改变网格形状从而提高精确度,使得车架横梁的连接位置得到优化,改善应力集中现象,使最大应力值下降5.3%.胡志峰[6]采用网格参数化方法,通过网格变形控制改变参数变形体形状,从而找到车体侧墙筋板最合适的布置角度完成形状优化。周杭[7]采用加权组合处理分拣小车工况,并使用变密度法(SIMP)进行结构拓扑优化,轻量化效果明显,质量减少了29.8%.阎力[8]基于有限元理论,使用有限元软件对FSC赛车车架前舱进行局部拓扑优化,对车架管径进行尺寸优化,质量减少15.6%.
结构优化过程中每个步骤都可能用到不同的优化方法,在此使用Ansys对模型进行直接离散化的网格划分,保证一定的精确度。对于载荷工况选择参照欧洲标准考虑整体工况,确定几种主要载荷,然后通过组合计算方法选择组合工况,从而确定优化工况。在此主要对车体构件进行尺寸优化,优化时为了提高计算精度对变量进行分组对比研究。
1 基于有限元的车体结构分析
1.1 车体结构有限元模型的建立
由于车体的薄壳结构并且其主要承受弯曲变形载荷,在Ansys中建模时选择4节点6自由度的壳单元shell63.转向架支座采用实体单元solid45.在车体结构计算中,选用COMBIN14单元模拟转向架对车体的支撑作用。车下吊装设备,桌椅等地板附属设备采用质量单元mass21加在相应的位置上。然后按照车体原结构进行模型简化,步骤如下:
(1)采用壳单元shell63模拟车体截面形状,在离散结构时对其定义相应的厚度,从而保证计算精度,简化结果见图1;
(2)对整车结构变形及应力分布影响很小的非承载构件忽略不计;
(3)对结构强度影响较小、因制造工艺而增加的细小倒角和圆角简化为直角,从而降低网格划分的困难;
(4)构建表面光顺滑;
(5)对两个靠的近却不重合的交叉连接点简化为一个节点处理。

图1 简化后车体截面图Fig.1 Simplified cross section diagram
通过车体结构分析,采用节点耦合的形式模拟焊接结构,以质量块的方式施加在相应节点的方法进行附件质量的模拟,采用复合单元实现板单元与实体单元之间的过渡,将车体几何模型离散化,进行网格划分并施加约束及边界条件后,生成最终需要的有限元模型(见图2)。有限元仿真模型的节点总数为99 533,单元总数为150 115.

图2 车体有限元模型Fig.2 FE model of vehicle body
1.2 车体刚度、强度有限元仿真分析
参照《UIC566》与《EN12633》标准[9-10],对各种工况进行分析,车体所受约束和载荷通常在车钩连接处、车端部、转向架等位置。车体在各种工况下的约束位置用有限元分析表示如图3所示,载荷位置用有限元分析表示如图4所示(其中X轴沿车体横向,Y为垂直方向,Z轴沿车体纵向由一位端指向二位端)。

图3 车体有限元分析约束位置Fig.3 Constrain locations of M2S bodyshell FEA

图4 车体有限元分析载荷位置Fig.4 Load locations of M2S bodyshell FEA
1.2.1 载荷工况选取
参考欧洲标准EN12663考虑车体的载荷工况,文献[11]中对单一工况进行组合计算,考虑车体所受主要载荷,得到十种主要组合工况,然后根据有限元仿真结果分析,确定最终优化工况,即:工作载荷状态下,对车钩再施加水平方向的1 500 kN压缩载荷。该工况下的应力云图和位移云图见图5、图6.

图5 应力云图Fig.5 Maximum stress contour

图6 位移云图Fig.6 Displacement on body structure
分析可知,该工况下最大应力出现在二位端靠近内端墙的门角(见图5),应力值为184.3 MPa,底架边梁的最大垂向位移是4.26 mm.车体车钩水平位置承受压缩载荷,车体车钩区域承受纵向压缩载荷时,主要通过内外主筋板以及辅助筋板传递给车体,所以这些筋板是重要的承载部位,会产生比较大的应力。而受垂向载荷作用时,门和窗户对侧墙强度有较大削弱,所以会在附近产生应力集中。此时车体满足强度和刚度的设计,结构存在优化减重的潜力。
1.2.2 车体结构刚度分析
在确定的优化工况下,采用增大刚度的方法考察车顶、侧墙及车底对车体整体刚度的影响,从而通过有限元仿真结果确定优化对象。
(1)增大车顶刚度,由应力云图分析得最大应力出现在二位端靠近内端墙的门角处,应力值为171.616 MPa,底架边梁的最大垂向位移为3.348 mm.车体整体应力云图及其位移云图见图7、图8.

图7 应力云图Fig.7 Maximum stress contour

图8 位移云图Fig.8 Displacement on body structure
(2)增大侧墙刚度,由应力云图分析得最大应力出现在二位端靠近内端墙的门角处,应力值为230.209 MPa,底架边梁的最大垂向位移3.062 mm.车体整体应力云图及其位移云图见图9、图10.
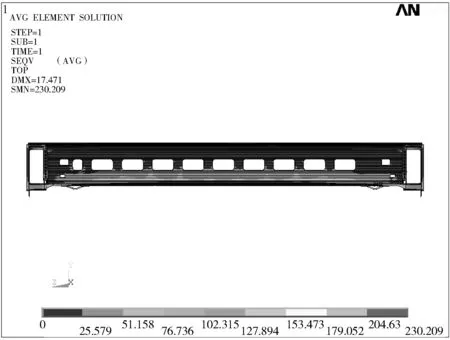
图9 应力云图Fig.9 Maximum stress contour
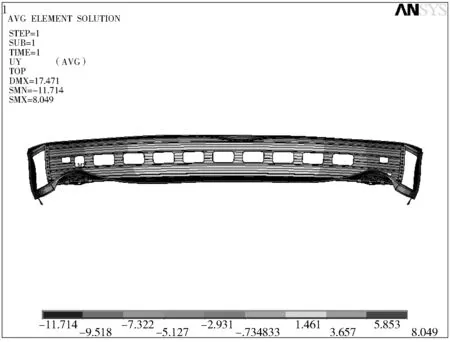
图10 位移云图Fig.10 Displacement on body structure
(3)增大底架刚度,由应力云图分析得最大应力出现在底板孔处,应力值为198.316 MPa,底架边梁的最大垂向位移1.914 mm.车体整体应力云图及其位移云图见图11、图12.

图11 应力云图Fig.11 Maximum stress contour
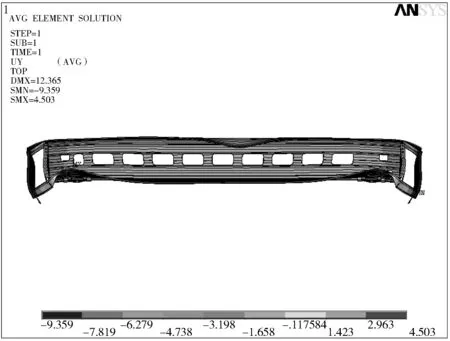
图12 位移云图Fig.12 Displacement on body structure
从以上分析及车体刚度评价标准可知,在增加相同刚度的条件下,底架刚度的变化对车体整体刚度的影响最为有效,而车顶和侧墙刚度的变化对车体整体强度的影响最为有效。综合考虑车体整体的应力和位移,以底架为结构优化对象。
2 车体底架的尺寸优化
2.1 数学模型
面对实际问题,我们需要将优化问题转化为数学问题,从而确定设计方案。
(1)设计变量:以底架上下盖板以及肋板的厚度作为设计变量。可以用矩阵表示为:
X={X1,X2,…,Xm]T
(1)
(2)约束条件:要根据强度和刚度的评价标准,充分考虑车体许用应力变化范围及其底架垂向位移大小等约束条件。
强度约束条件:
σmaxi≤σ,(i=1,2,…,n)
(2)
其中n为设计变量。
刚度约束条件:
(3)
其中L为底架边梁的最大垂向位移;a为车体定距为19 000 mm.
(3)目标函数:以车体重量为目标函数。
目标函数可以表示为:
Minf(X)=f(X1…X2,…,Xn)
(4)
因此,其数学模型表示如下:
Minf(X)=f(X1,X2,Xn)
S.t.σmaxi≤σ,(i=1,2,…,n)
2.2 优化对象
由前面分析可知,优化对象为车体底架,为方便设计,变量的分组大致分为3个板块(见图13中标记区域),优化工况为工作载荷状态下,对车钩再施加水平方向的1 500 kN压缩载荷,优化的目标函数为车体的重量,底架边梁的垂向位移和最大应力为约束条件。

图13 优化对象
Fig.13 Optimized object
2.3 变量的分组
使用OptiStruct软件对M2S车体底架进行尺寸优化,为了减少优化求解的计算量,采用分组的方法,把设计变量分成以下五组:
(1)上下盖板厚度为一个变量,每块肋板厚度为一个变量,共25个变量;
(2)上下盖板厚度为一个变量,成倒三角的相邻两块肋板厚度为一个变量,共13个变量;
(3)上下盖板厚度为一个变量,第一块板的肋板2组变量,第二、三块板的肋板每组3个变量,共9个变量;
(4)上下盖板厚度为一个变量,每块板的肋板2组变量,共7个变量;
(5)上下盖板厚度为一个变量,每块板的肋板为一个变量,共4个变量。
2.4 优化结果及分析
为了得到更精确的优化结果,分别进行基于连续变量和离散变量的尺寸优化,优化前的质量为4 212 kg,最大应力为184.3 MPa,底架边梁最大垂向位移为4.26 mm,优化后结果如表1、表2所示。
表1 基于连续变量的尺寸优化
Tab.1 Size optimization based on continuous variables

分组1Group1分组2Group2分组3Group3分组4Group4分组5Group5 质量/kg3 868.73 8703 870.83 871.23 873.4 最大应力/MPa197.67197.45190.37190.24190.21 底架边梁最大垂向位移/mm4.584.033.953.943.92
表2 基于离散变量的尺寸优化
Tab.2 Size optimization based on discrete variables

分组1Group1分组2Group2分组3Group3分组4Group4分组5Group5 质量/kg3 862.43 865.43 865.83 867.43 872.9 最大应力/MPa197.37197.03191.18191.68189.89 底架边梁最大垂向位移/mm4.584.034.504.503.89
由表2可知,基于离散变量的尺寸优化效果更好。理论上尺寸变量连续变化,取值范围大,优化效果好,但由于对连续变量的值做了向上的保守圆整,反而导致优化结果较差,此次优化说明基于离散变量尺寸优化是可行的。离散变量和连续变量从分组来看,变化趋势一致,但是使用离散变量的尺寸优化整体效果较好。
3 结论
通过对CRH5动车组M2S车体结构分析,对车体模型进行适当简化,根据各部件受力特点,选取合适的单元模型并进行网格划分等操作。参考欧洲标准对车体有限元模型施加约束和载荷,对单一工况进行组合计算后进行有限元仿真分析,综合分析结果确定最终优化对象和典型载荷工况,采用减少计算量的变量分组法分别进行基于连续变量和离散变量的尺寸优化。经分析对比,基于连续变量的尺寸优化使车身质量最高下降8%,基于离散变量尺寸优化使车身质量下降8.3%.本研究采用的轻量化途径证明是可行的。

