基于模糊-PID的油膜轴承试验台调速系统设计

侯定邦，王建梅，王 宁，王生龙

(太原科技大学重型机械教育部工程研究中心；太原重型机械装备协同创新中心，太原 030024)

我校自主研制的油膜轴承试验台可以在任意模拟工况下采集轴承中油膜的实时参数。保障模拟工况的精确性对提高测试数据的精度有着重大作用，因此对试验台电机转速的控制提出了要求。在工业过程控制应用中，超过95%的直流电机控制器是PID类型，但其在需要模拟突变工况时无法满足其高精度的控制需求。为了能够精确模拟轧制过程中出现的转速突变等情况，有必要设计性能更加优秀的控制系统。PID模糊逻辑控制器的最大优点正是其可以人为积累的工作经验固化为一套完整的控制规则，在工况突变时自动选取恰当的策略应对问题，从而满足本试验台对电机转速的要求[1-2]。

L.A.Zadeh教授提出了模糊数学[3]，模糊逻辑在工控领域得到普遍认可及应用[4]。模糊控制因其独特的构架常常拥有佳的控制效果，在应对复杂的机电系统时更游刃有余[5]。杨彪等应用模糊 PID 算法实现了对微波加热的控制[6]；Zhao Z Y等的研究论证了模糊PID控制器的优越性[7]；Li S和Liu Z.提出了一种自适应控制方案用以永磁同步电动机的调速系统[8]。

在结合已有研究方法和仿真结构的基础上，为了提高油膜轴承试验台直流电机的控制精度，本文提出在直流电机调速控制系统中采用模糊PID控制策略，依据试验台电机建立了数学模型，并通过仿真分析验证了该控制策略的科学性。同时进一步将模糊PID的控制方法通过SCL语言应用于以S7-300PLC为控制核心的油膜轴承试验台主电机的调速控制系统，得到了良好的控制精度，使试验台能够更好地模拟情况复杂的轧制工况。

1 试验台电机控制单元的数学模型

1.1 直流电机数学模型

现有设备的调速原理是以输入电枢电压为信号量控制输出转速[9,10]。考虑到设备上采用的主电机是他励模式，能够推出他对应的数学模型如下式。

(1)

其中：

式中:具体参数含义如表1

表1 参数表
Fig.1 Parameter list

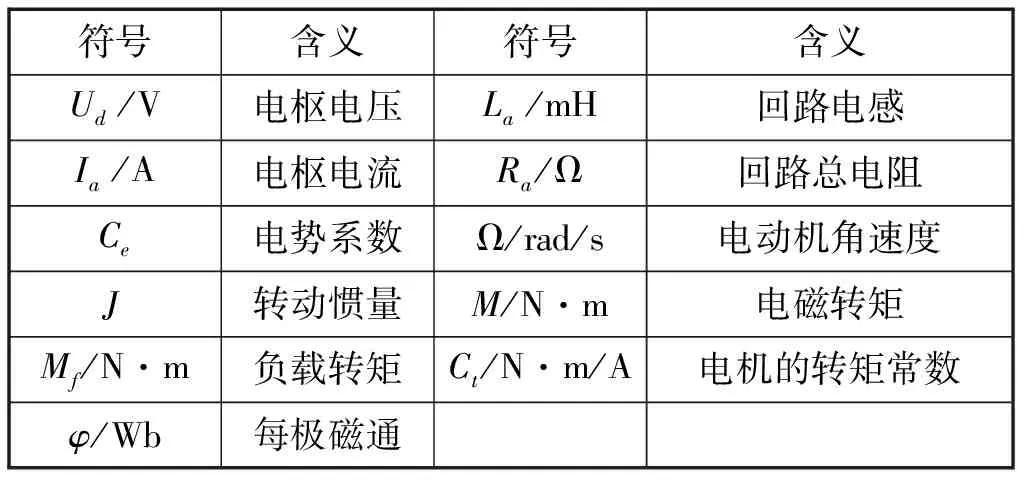
符号含义符号含义Ud/V电枢电压La/mH回路电感Ia/A电枢电流Ra/Ω回路总电阻Ce电势系数Ω/rad/s电动机角速度J转动惯量M/N·m电磁转矩Mf/N·m负载转矩Ct/N·m/A电机的转矩常数φ/Wb每极磁通

当外部空载时，Mf=0，且Ω=2πn，就能够推出电机转速的微分方程：

(2)

其中：Ta表示电磁时间参数；Tc表示时间参数；n表示转速。由此可以推出电压值与转速值的传递函数是：

(3)

1.2 整流器数学模型

如果不考虑晶闸管存在的压降，输出电压Uf可以由式(4)得到：

(4)

其中：U2表示交流侧的输入电压值，单位为V；β表示移相控制触发角。UG表示机端电压；nlc表示励磁变压器的变比。其中，U2=UG/nlc，这样可以推出：

Uf=(1.17/nlc)UG+(1.17/nlc)UGcosβ

(5)

ΔUf=KZ1ΔUG+KZ2Δβ

(6)

其中：

KZ1=[(1.17/nlc)+(1.17/nlc)cosβ]UG=UG0,β=β0

KZ2=[-(1.17/nlc)UGsinβ]UG=UG0,β=β0

式中：ΔUf是励磁电压Uf的增量；

Δβ和ΔUG分别表示对应变量的增量。再进一步进行拉氏变换可以推出：

Uf(S)=KZ1UG(S)+KZ2β(S)

(7)

励磁调节器中的输出信号与输入信号间存在滞后情况。其滞后TZ时间的最大可能值为：

TZ=1/(mf)

(8)

则其输出电压为：

Uf=KZβ(t-TZ)

(9)

式中：KZ是Uf与β之间的放大系数。

通过拉普拉斯变换可得：

Uf(S)=KZe-TZSβ(S)

(10)

整流器的传函得出：

UG(S)=Uf(S)/β(S)=KZe-TZS

(11)

根据实际中TZ数值很小，将上式中的e-TzS用泰勒展开式表达，可以得到：

(12)

不考虑展开式中的高次项，可以得到相应的传递函数为：

UG(S)=KZ/(1+TZS)

(13)

晶闸管移相触发装置的拟合方程[11]为：

Δβ=KXΔUg

(14)

式中，ΔUg表示Ug的增量，V；KX是对应的放大系数；

进一步求其拉氏变换：

β(S)=KXUg(S)

(15)

其相应的传递函数为：

β(S)/Ug(S)=KX

(16)

2 直流电机转速的模糊-PID控制器设计

2.1 模糊-PID控制策略

模糊-PID控制策略以偏差信号e以及偏差的变化速率ec作为输入，通过参与预设模糊规则表的分析比对，选出最佳控制参数，进而达到调节被控系统的控制性能的目的。图1是其原理示意。

图1 模糊-PID控制系统结构图Fig1 Fuzzy-PID control system structure diagram

2.2 试验台电机模糊-PID控制器设计

2.2.1 各变量隶属度函数的确定

输入偏差信号以及偏差变化率的模糊子集常用{DF，ZF，XF，O，XZ，ZZ，DZ}表示。依据现有设备使用情况，将论域设为(-3，-2，-1，0，1，2，3)。同步设计了对应控制参数KP，KI，KD的模糊子集。依据现有设备实际参数，输入与输出分别选择了高斯和三角型隶属函数，具体曲线见图2和3。

ΔKP、ΔKI和ΔKD在论域上的输出曲面如图4所示。

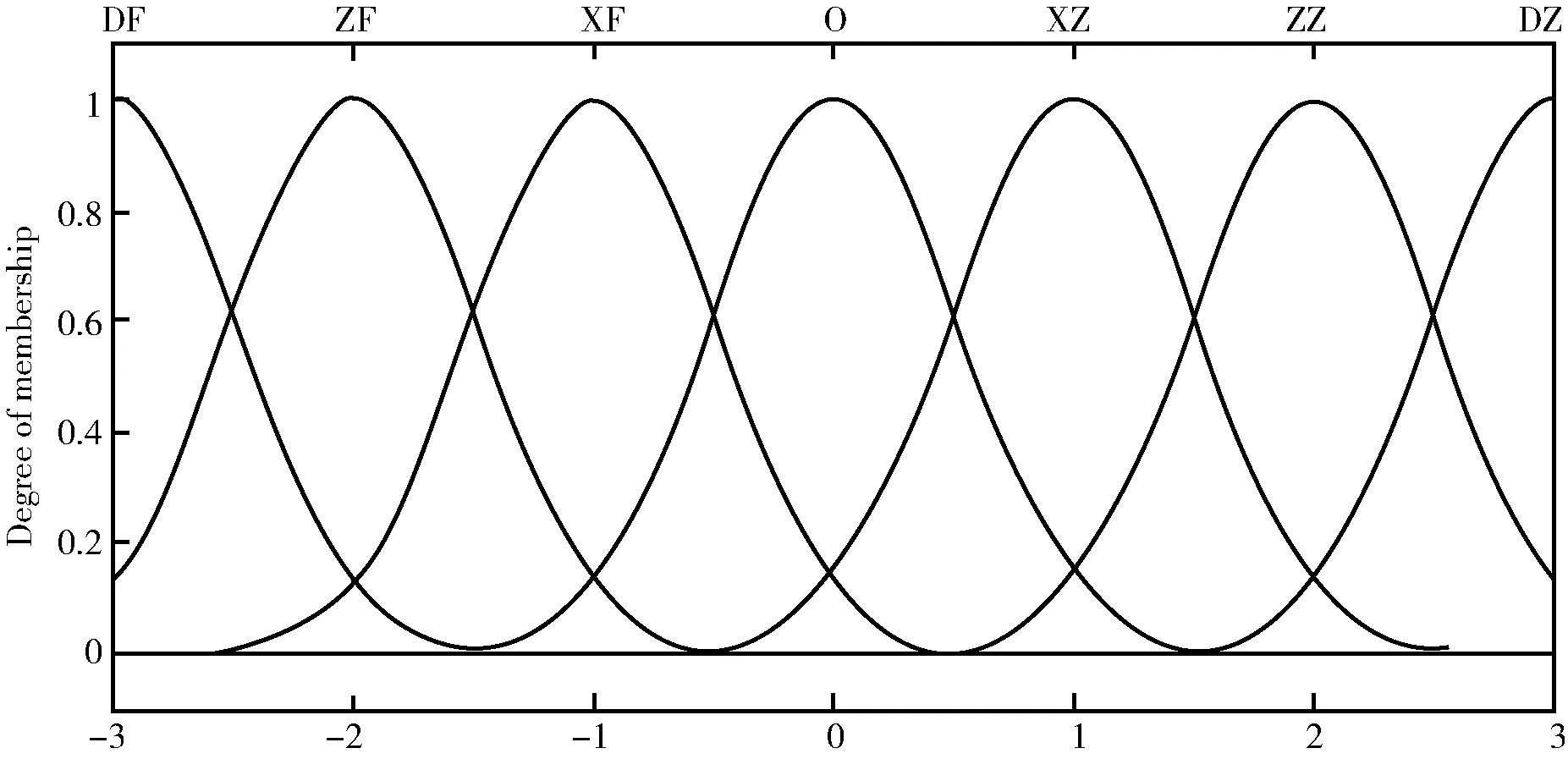
图2 输入的隶属函数图

Fig.2 Input membership function graph

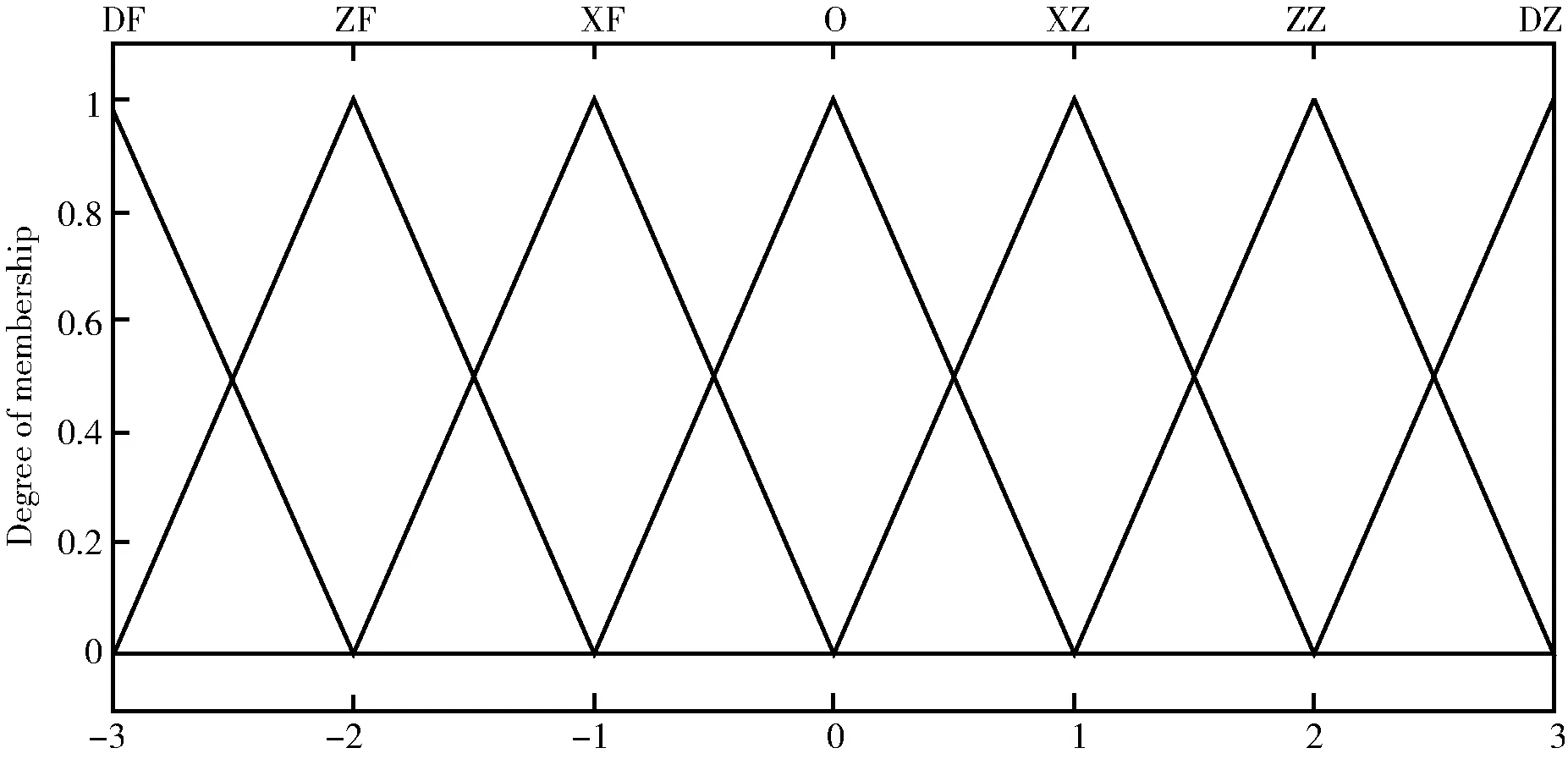
图3 输出的隶属函数图

Fig.3 Output membership function graph

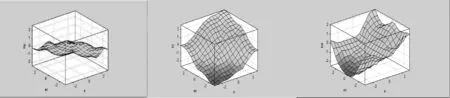
图4 ΔKP、ΔKI和ΔKD在论域上的输出曲面Fig.4 The output surface of ΔKP、ΔKIandΔKDon the universe

2.2.2 参数整定

结合文献、实际操作经验以及现有设备运行情况，总结出三个控制参数KP，KI，KD的规则表2-表3。

表2 ΔKP模糊控制规则表
Tab.2 Fuzzy control rules table of ΔKP

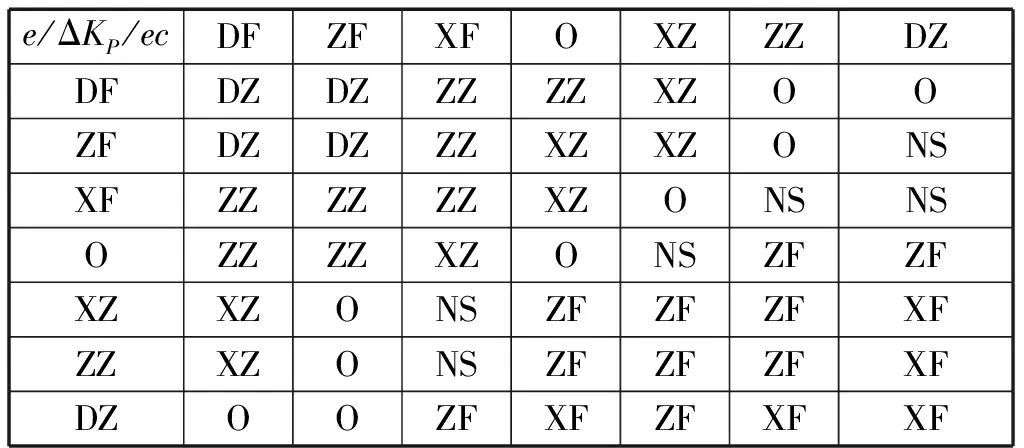
e/ΔKP/ecDFZFXFOXZZZDZDFDZDZZZZZXZOOZFDZDZZZXZXZONSXFZZZZZZXZONSNSOZZZZXZONSZFZFXZXZONSZFZFZFXFZZXZONSZFZFZFXFDZOOZFXFZFXFXF

表3 ΔKI模糊控制规则表
Tab.3 Fuzzy control rules table of ΔKI

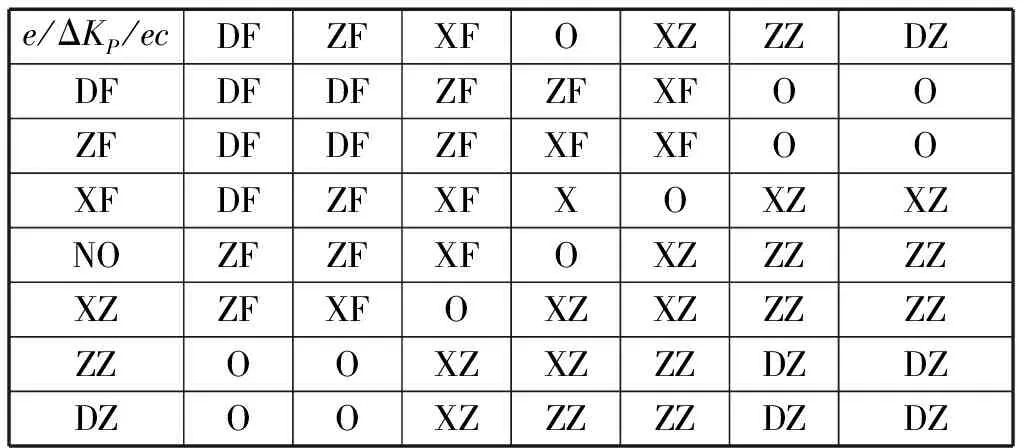
e/ΔKP/ecDFZFXFOXZZZDZDFDFDFZFZFXFOOZFDFDFZFXFXFOOXFDFZFXFXOXZXZNOZFZFXFOXZZZZZXZZFXFOXZXZZZZZZZOOXZXZZZDZDZDZOOXZZZZZDZDZ

表4 ΔKD模糊控制规则表
Tab.4 Fuzzy control rules table of ΔKD

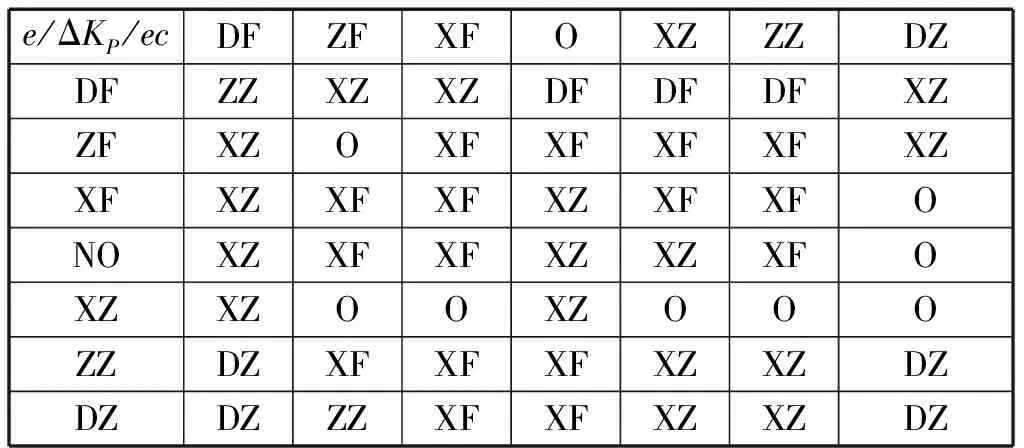
e/ΔKP/ecDFZFXFOXZZZDZDFZZXZXZDFDFDFXZZFXZOXFXFXFXFXZXFXZXFXFXZXFXFONOXZXFXFXZXZXFOXZXZOOXZOOOZZDZXFXFXFXZXZDZDZDZZZXFXFXZXZDZ

另外，PID参数调整公式如下：

*KP=KP+ΔKP

(17)

*KI=KI+ΔKI

(18)

*KD=KD+ΔKD

(19)

式(17)-(19)中，KP，KI，KD为PID参数的初始值。

3 MATLAB仿真分析

基于MATLAB/Simulink仿真平台搭建电机转速控制模型进行仿真分析。

3.1 直流电机PID调速系统仿真模型建立

如图5所示是转速控制系统的Simulink仿真框图。

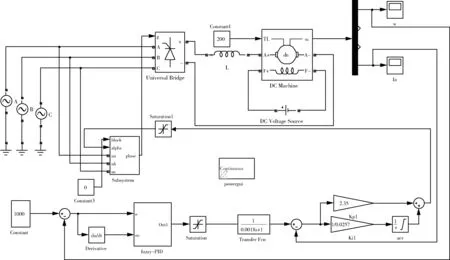
图5 模糊-PID转速控制系统仿真框图Fig.5 Fuzzy-PID control simulation block diagram on speed control system

3.2 仿真结果分析

试验台的电机和控制回路参数见表5：

表5 参数取值
Tab.5 Parameter selection

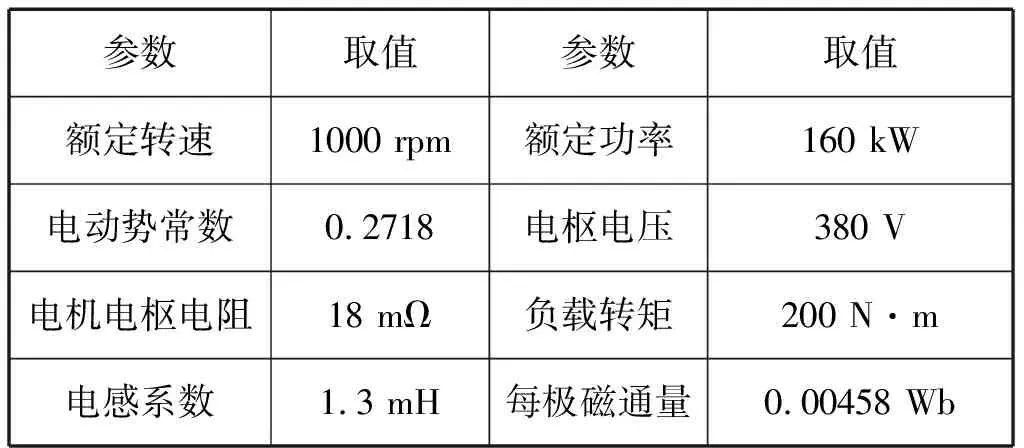
参数取值参数取值额定转速1000 rpm额定功率160 kW电动势常数0.2718电枢电压380 V电机电枢电阻18 mΩ负载转矩200 N·m电感系数1.3 mH每极磁通量0.00458 Wb

根据工程整定方法确定PID相关调节参数并设为初始参数进行仿真。选取两种不同的速度设定值100、300，研究其速度由零初始的阶跃响应情况。PID与模糊PID的控制策略仿真结果如图6-图7所示。其中，左侧为PID控制，右侧为模糊PID控制。

由图6和7可知，在高速以及低速情况两种情况下，模糊-PID控制器较经典PID都有较快的响应速度和较低的超调量，所以应用模糊-PID控制策略可以提高设备的控制精度。

图6 100 rpm系统仿真结果对比Fig.6 Comparison of system simulation results at 100 rpm

图7 300 rpm系统仿真结果Fig.7 Comparison of system simulation results at 300 rpm

4 电机转速模糊-PID控制系统的PLC实现

4.1 试验台调速系统组成

试验台调速系统包括120KW的直流电机、直流调速设备、西门子S7-300PLC、工控机及相应的手动操作台。工作过程为PLC控制调节直流电机进而驱动试验台三组油膜轴承运转模拟轧制过程实际工况。油膜轴承调速控制系统如图8所示。

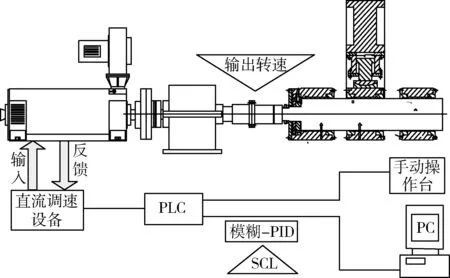
图8 调速系统组成Fig.8 Speed control system

5 WinCC界面

在直流电机转速的模糊-PID控制过程中，监控画面利用WinCC组态功能进行开发，在工控机上对电机转速的设定值和过程值进行了采集归档，并通过历史曲线进行记录分析。

其相应的控制曲线如图9和10。其中红线为设定值，蓝线为实际转速。由这两幅图分析可得，模糊-PID控制和常规PID控制电机转速相比，前者响应时间短，超调量小。

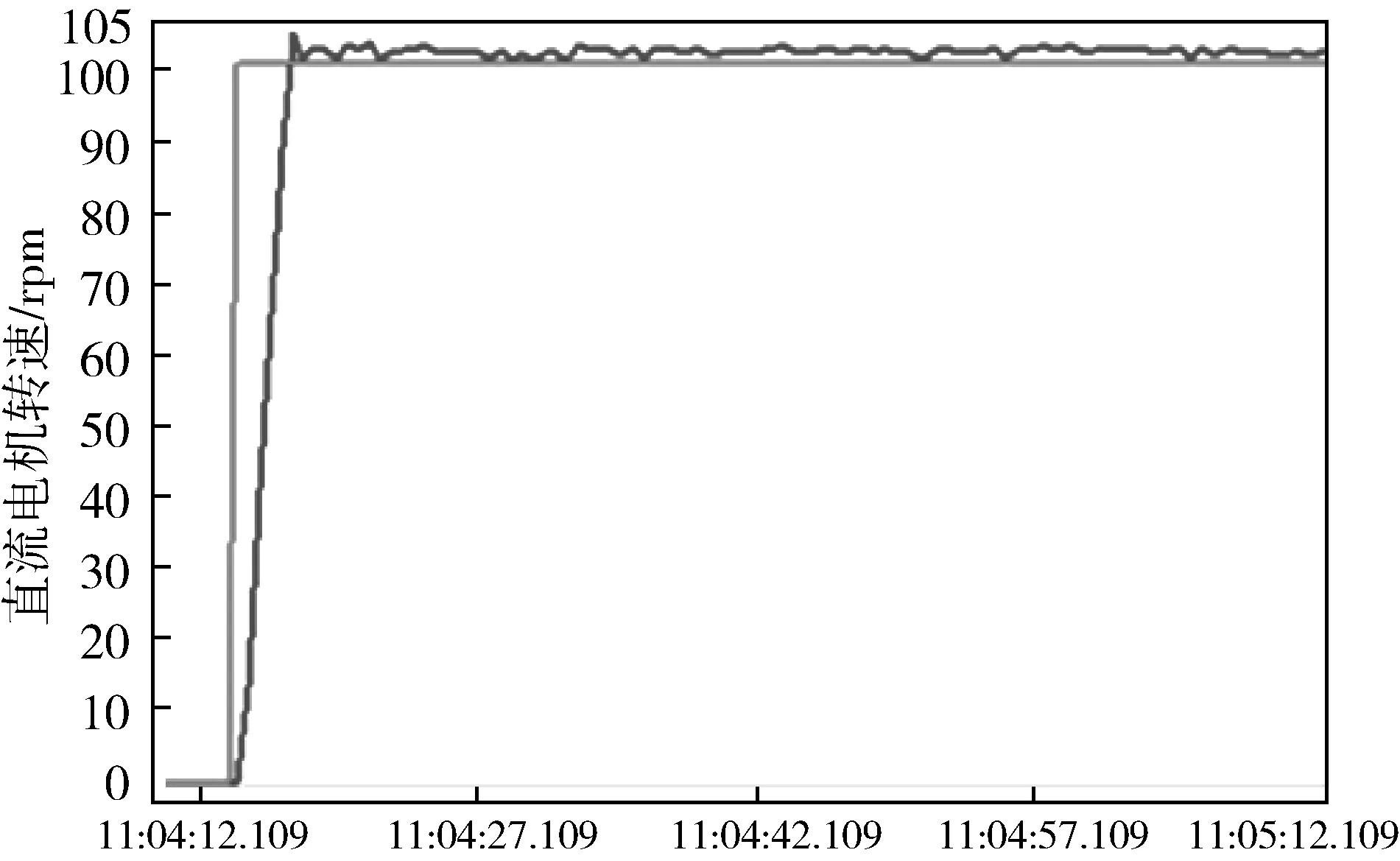
图9 常规PID转速响应曲线Fig.9 Speed response curve for traditional PID control

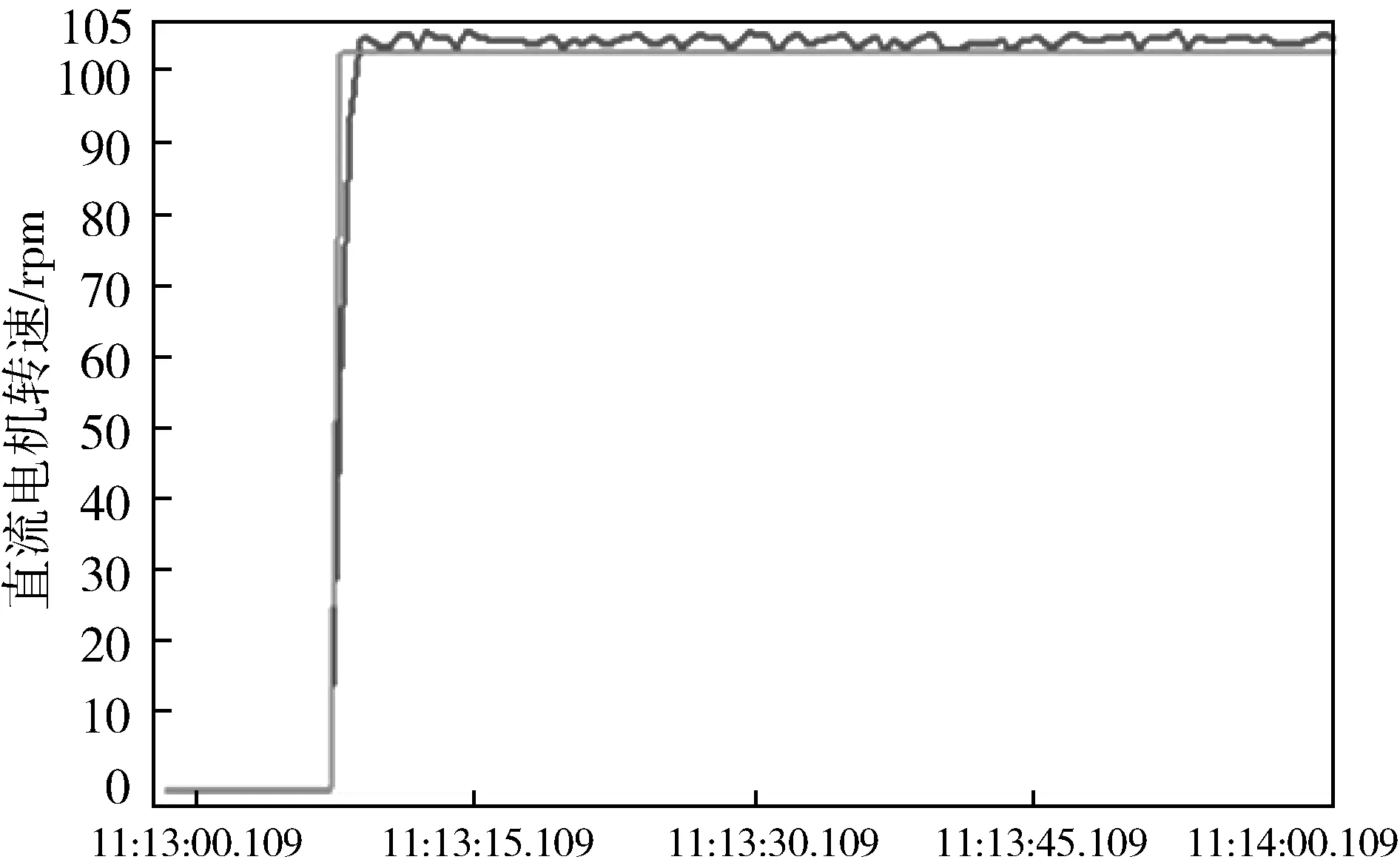
图10 模糊-PID转速响应曲线Fig.10 Speed response curve for Fuzzy-PID control

6 结 论

(1)通过对传统PID控制方法与模糊-PID控制方法进行仿真分析，得出在不同的启动速度下，基于模糊-PID控制方法的系统响应速度比传统控制快，并且具有更小的超调量，即模糊-PID控制器能够提高转速控制精度。

(2)基于高级编程语言SCL设计了模糊-PID控制功能的PLC程序，并利用组态软件WinCC设计了试验台电机转速的曲线监测画面。通过对比模糊-PID控制策略下与传统PID控制策略下的电机速度响应曲线，研究发现，前者的控制效果与仿真结果吻合，能够有效地提高试验台电机的转速控制精度，

(3)通过引进模糊-PID控制方法，使油膜轴承试验台的电机控制精度大幅提高，综合性能得到进一步改进。