一种改进的公路事故多发路段处机动车安全风险评价方法

徐 鹏, 刘 昊

(天津市公安局网安总队， 天津 300384)

0 引言

交通事故多发路段是指受交通条件、道路条件和气候环境等因素的影响，在一段时间内发生的交通事故数量明显多于其他正常路段[1]。对公路事故多发路段的鉴别可以用于研究事故发生的主要影响因素，从而采取相应的措施以降低公路交通事故的发生。

目前国内外事故多发路段鉴别方法以累计频率曲线法[2-3]为代表的等距离划分方法为主，该类方法存在密集路段被人为拆分和短距离路段被强制扩散等问题。文献[4-5]提出了一种基于密度的DBSCAN聚类方法可以弥补上述不足，它根据数据对象周围密度的不断增长聚类，将密度足够高的区域内数据对象划分为簇，具有快速识别任意形状簇、处理数据对象中的噪声点的优点,但是单独基于密度聚类不能完全将事故严重程度考虑在计算范围内。现有的文献中对事故的研究大多仅限于事故多发路段的识别，很少对造成事故的因素进行分析，文献[6-7]分别从道路结构、道路线型、交通条件、路侧环境和驾驶员心理等角度对事故成因进行了分析。

针对上述问题，本文将提出一种改进的公路事故多发路段处机动车安全风险评价方法，文中对基于密度的DBSCAN聚类算法进行改进，将事故严重程度作为加权项考虑在内，算法聚类得出的事故多发路段不论是从事故数量上还是从事故严重程度上都体现出了事故的危害性。在识别出事故多发路段的基础上，进一步对车辆因素进行分析，提出一种基于重设阈值的累积逻辑回归算法来对事故多发路段中的车辆风险指数进行预测。

1 基本算法介绍

本文在分析过程中，主要使用DBSCAN聚类算法、KPrototype聚类算法和累积逻辑回归算法，以下分别对几种基本算法进行介绍。

1.1 DBSCAN和KPrototype聚类算法

DBSCAN和KPrototype是两类聚类算法，是无监督学习算法，训练样本的标记信息是未知的，其目标是通过对无标记训练样本的学习来揭示数据的内在性质和规律。DBSCAN算法是基于密度的聚类，该算法基于一组邻域参数来刻画样本分布的紧密程度[8]。KPrototype算法适用于混合数据，是基于原型的聚类，聚类结构能够通过一组原型刻画，然后对原型进行迭代更新求解，其中比较重要的一点就是需要预先指定聚类的簇数[9]。

1.2 累积逻辑回归算法

2 适应W-DBSCAN事故多发路段识别

本文对事故多发路段的识别主要从DBSCAN算法展开进行，从参数自适应和权重两方面分别进行了改进，使用累积频率曲线法中的事故阈值对Minpts进行初始化，使用事故严重程度对算法进行加权。

公安部《全面排查交通事故多发点段工作方案》中鉴定事故多发路段的标准为在一年内500米范围内发生3次以上交通事故的地点。因此，首先使用累积频率法以500米为步长划分路段进行分析，对数据进行归一化以后，建立双指数函数(y=abx+cdx+e)拟合累积频率曲线，使用已知事故频率数据对曲线中的参数进行计算，对得出的累积频率曲线进行曲率计算，找到曲率最大点并进行归一化还原得出事故数量阈值点。

图1 事故多发路段识别流程图

使用累积频率曲线法中的事故数量阈值点初始化密度阈值Minpts,使用500初始化领域半径ε，进行参数自适应DBSCAN。为了使模型能更高效、集中、足量地反映事故多发路段，现通过减少ε半径来降低事故多发路段总长度dblack占全部路段长度dall的比例和提高事故阈值Minpts来降低簇数C。于是对ε在[500,200]内以步长-50进行逐步遍历，当事故多发路段占比dblack/dall小于等于n时，进而对Minpts在[3,20]内以步长1进行逐步遍历，当簇数C小于等于m时，此时参数组合(ε，Minpts)满足条件，以此参数组合输出DBSCAN聚类识别的事故多发路段。

传统上，公安部按照人身伤亡或财产损失的程度和数额，将道路交通事故分为轻微事故、一般事故、重大事故和特大事故，如，轻微事故，是指一次造成轻伤1～2人，或者财产损失机动车事故不足1 000元，非机动车事故不足200元的事故。由于财产损失的估算存在主观性，本文中使用轻伤人数(QSRS)、重伤人数(ZSRS)和7日内死亡人数(SWRS7)3项指标对事故严重程度进行评价，并根据事故类型划分标准中指标间的对应关系计算指标权重，QSRS、ZSRS、SWRS7的权重分别为K1、K2、K2。例如一般事故指一次造成重伤1～2人，或者轻伤3人以上的事故，可得K2≥3K1；同样可根据重大、特大事故划分标准确定K3≥4K2，因此以K1=1为基础，得到一起事故的严重程度为y=1+QSRS+3ZSRS+12SWRS7，其中常数项1为事故次数。

3 基于RT-CLR算法的事故多发路段机动车风险评估

在识别出事故多发路段之后，一方面可以通过对事故多发路段的路况进行完善，设置警告标志等降低事故率；另一方面，可对进入事故多发路段的车辆根据车辆特征进行风险评估，对事故风险高的车辆进行重点观察并在警务通上进行风险提示，以此降低事故概率。根据车辆特征进行风险评估的方法可采用逻辑回归，一方面逻辑回归不要求自变量和因变量之间线性相关，另一方面，逻辑回归的输出为0～1之间的小数，可作为预测的概率直接输出。

图2 机动车安全风险评估流程

因为事故量最多的事故多发路段的事故量也不足以进行回归分析。同时，由于道路间不同的物理属性，在不同道路类型上事故易发的车辆可能具有不同的特征，若对所有事故样本一视同仁，放在同一个回归模型中进行拟合也会影响最终的结果。因此，首选需要对全部的事故多发路段进行聚类，将具有相同属性的路段聚类到一起，再对同类路段中的车辆进行风险评估，模型的具体实现流程如图2所示。

3.1 事故多发路段聚类

因为在回归分析时仅有事故样本还不够，所以需要卡口数据来构建非事故样本，因此智能选择全部路段中的带卡口的事故多发路段作为样本进行分析，其中带卡口路段是指该路段5 km范围内有卡口。

由于路段聚类是在识别出事故多发路段的基础上进行的，已经确定路段事故风险较高，因此聚类特征只需关注路段本身属性，可用的数据有事故录入数据和卡口过车数据。事故录入数据中与路段相关的字段有横断面位置、道路安全属性、路侧防护设施、道路物理隔离、路面状况、路面结构、路口路段类型、道路线型和地形共9个。可取上述9个字段作为描述事故多发路段静态信息的特征，同时从卡口过车数据中提取路段的年车流量和大车混入率作为描述事故路段动态信息的特征，如表1所示。

表1 路段聚类特征说明

使用KPrototype算法基于上述特征将带卡口的事故多发路段聚类为类，其中取值为1到9，最后使用肘部法则确认值，找到特征相同的路段。

3.2 机动车安全风险评判

以标记过的事故数据作为累积逻辑回归中的正例，同时结合卡口信息，对未发生交通事故的车辆信息进行“无事故”的标记。交通事故因素主要为人员、车辆、道路、环境因素。其中由于对车辆的风险评估是基于卡口摄像头采集到的信息实时进行的，很难捕捉到具体的驾驶人信息，同时由于已经对道路特征做了聚类，因此回归模型是在道路特征相近的样本上进行的，也就不需对道路特征进行建模，因此主要考虑车辆因素、环境因素。

从环境因素看，Kwon等在其道路安全风险因素分类算法应用研究中，使用了时间、天气等指标[11]。从车辆因素看，吴剑在行车风险评价研究中采用车辆类型、车辆性能、车辆技术状况等作为机动车与非机动车对交通安全的影响因素[12]。因此基于前人研究基础，具体选取样本特征如表2，共11类：

表2 机动车安全风险评价特征

由于事故样本和无事故样本数量严重失衡，因此采用重设阈值的方式进行样本均衡。在样本标记中，0为未发生交通事故，1为轻微事故，2为一般事故，4为重大事故，8为特大事故，由于重大事故和特大事故样本量小，不具有一般性，因此不再对他们在累积回归模型中单独划分正例。分别以y>0，y=1和y≥2为正例构建累积逻辑回归模型，对训练集进行训练。使用10折交叉验证对每次训练的结果进行平均得出风险机动车。

4 算法实验

统计境内某公路一年内的路段事故信息，归一化后得到如表3所示的累积事故信息，使用双指数函数(y=abx+cdx+e)拟合累积频率曲线，得到如图3所示的公路事故累积频率曲线图，拟合度R2=0.999 36，拟合曲线方程为：

y=-262.081×1.000 3x+0.937×(3.35e-6)x+262.142

表3 境内某公路事故路段累计频率表

将归一化事故次数0.23乘以路段最大事故数换算成路段事故次数即0.23×11=2.53，得到该道路事故多发路段的事故阈值Minpts=3。根据事故路段累计频率表，可以得出事故次数大于等于3的路段为事故多发路段，共124个路段，占比8.01%，事故多发路段发生的事故总数为561起，占比51.71%。将相邻的事故多发路段连接，得到拼接后的事故多发路段共91簇，最终结果如图4所示。

图3 路段累计频率曲线拟合效果

图4 累计频率法鉴别出的事故多发路段

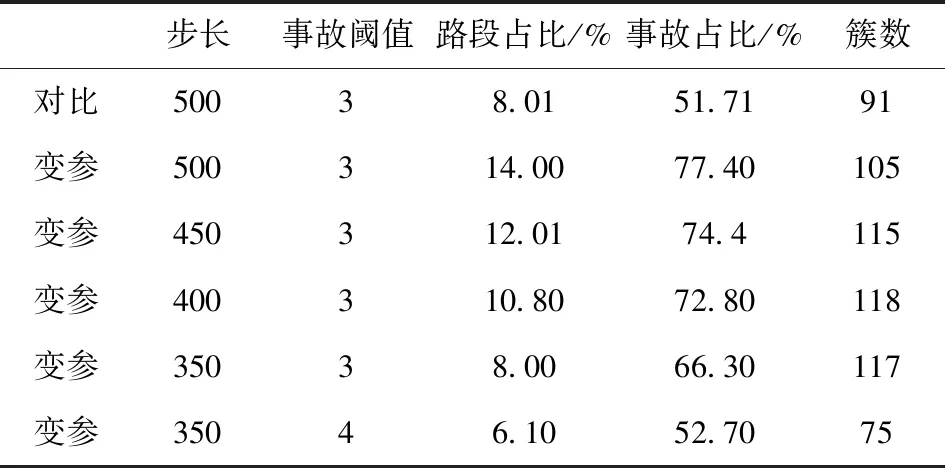
表4 DBSCAN变参过程

如表4所示，当参数组合调整为(ε=350，Minpts=4)时：DBSCAN的路段占比为6.1%，小于累计频率曲线识别结果的路段占比8.01%；事故占比为52.70%，大于累计频率曲线识别结果的事故占比51.71%；同时路段簇数为75，小于累计频率曲线识别结果的91簇。可见参数组合(ε=350，Minpts=4)的DBSCAN聚类结果满足“高效，集中，足量”的三个目标，因此采用这一参数组合作为最终参数进行聚类，得到最终的结果如图5所示。

图5 DBSCAN鉴别出的事故多发路段

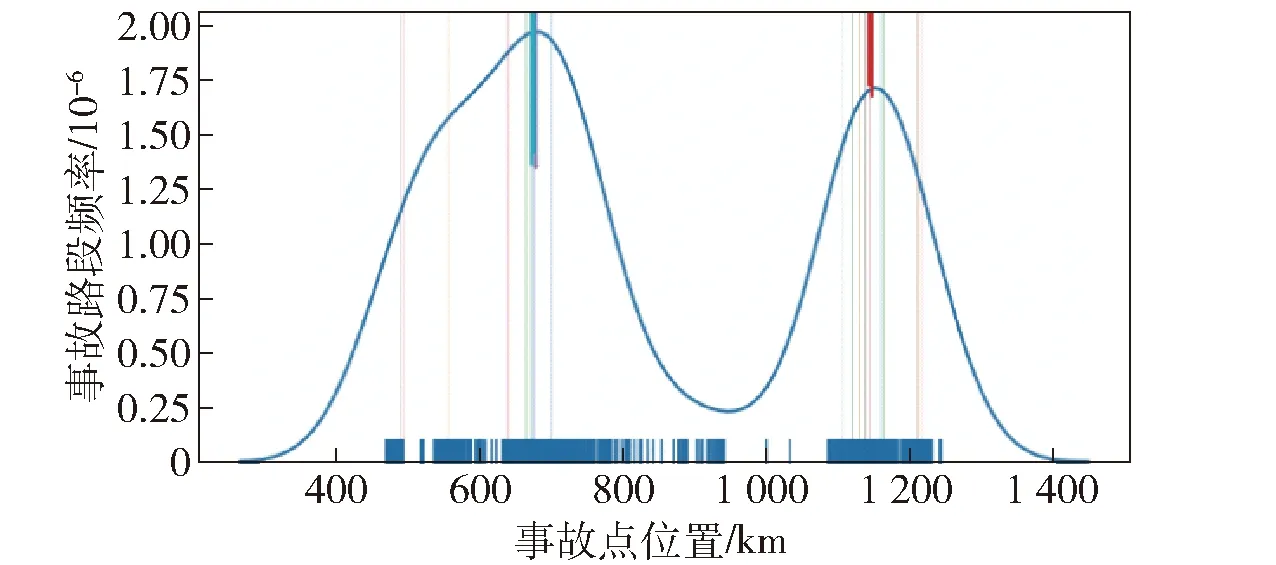
图6 加权DBSCAN鉴别出的事故多发路段

基于DBSCAN的事故多发路段鉴别法在事故数量的鉴别上更为高效，鉴别出的事故多发路段的每公里事故量为12.11，大于用累计频率曲线法得到的9.05，用了更短的事故多发路段反映了更多的事故量；另外DBSCAN聚成的多发路段簇数为75，小于累计频率法的91簇，反映出的事故多发路段更为集中；基于事故加权的DBSCAN算法把事故的严重程度也考虑在内，能够更加客观的对事故多发路段的危害进行评价。

图7 不同聚类簇数的平均畸变程度

对境内某区域各条公路分别进行事故多发路段识别，共得到事故多发路段1 651个，从中选取5 km范围内有卡口的552个路段作为样本进行分析，分别取聚类簇数为1～9的聚类效果如图7所示，由肘部法则得到聚类簇数k=2时，推荐的结果最好，观察两类事故多发路段中相差最大的特征分别是道路物理隔离、路面结构和地形。其中类别簇数标记为0的事故地点道路物理隔离为中心隔离、路面结构为沥青、地形为平原，标记为1簇数的事故地点物理隔离为无隔离、路面结构为水泥、地形为山区，其余特征在两个簇中较为一致，具体两类簇中的属性信息如表5所示，其中连续变量取均值，类别变量取众值。

表5 两类路段特征分布

因为地形为平原的地区更具有普遍性，本文只针对两类路段中的第一类进行分析。得到第一类路段中发生事故，轻微事故和伤亡事故的累积Logistic概率模型分别为：

其中的logit(P1)为不发生事故对发生事故的优势比，logit(P2)为发生轻微事故对发生一般及以上事故的优势比，logit(R2)为发生轻微或一般事故对发生重大事故的优势比。在10折交叉验证中，依次以上述累积回归模型对测试集进行检验，以0-1错误率作为指标衡量模型的精确度：

其中n为测试样本量，y′为对样本类别的估计值，y为样本类别的真实值，由于y的输出为0或1。进行10次测试，对比普通累积逻辑回归算法和重设阈值的累积逻辑回归算法的预测结果的平均值如表6所示。

可见重设阈值的累计逻辑回归模型对各个分类的识别精确率都在70%以上，对于样本车辆是否发生事故的预测精确度在95%以上，比普通的累积逻辑回归算法准确率平均提升4.9个百分点，可以用来有效识别事故多发路段处车辆的事故发生情况，做出及时预警。

表6 逻辑回归预测结果

5 结论

(1)与传统累计频率曲线法相比，使用DBSCAN聚类法鉴别事故多发路段能更集中有效地反映多发路段，表现为事故多发路段长度占比更少，事故数量占比更高。

(2)使用正则化目标函数下的参数自适应能实现最优参数的自调整，有效解决了密度聚类中参数难以定值的问题，可使聚类结果簇数更少，事故多发反映更集中。

(3)对事故严重程度进行加权而识别出的事故多发路段能淡化事故数量多但严重程度不高的路段，强化事故严重程度高的路段，聚类效果更优。

(4)采用累积逻辑回归对事故多发路段的通行车辆进行预警能有对车辆是否发生事故进行有效预测，模型精度达到了95.6%。