打破砂锅问到底——一道习题的追问与变式

文刘玉兵

例［苏科版八（上）第一章第31页习题1.3第8题］已知：如图1，在△ABC中，AB=AC，BD、CE为高，求证：BD=CE。

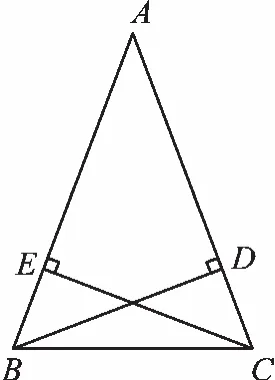
图1

【分析一】由三角形面积的两种不同表示方法可以得到：当三角形的面积和底边分别相等时，高一定相等。

【分析二】把BD、CE分别放到两个三角形中，证明三角形全等，再由全等三角形的对应边相等推出BD=CE。

【小结】在几何学习中，由于惯性思维，很多同学不易想到分析一，其实面积法往往更简洁、高效。分析二关键在于把BD、CE分别放到哪两个全等的三角形中去，选择何种全等三角形的证明方法，这里要注意公共角∠A的作用。

【追问一】如图2，在例题的基础上，试问△BDC和△CEB是否全等？

【分析】要证△BDC和△CEB全等，首先要判断这是两个直角三角形，其次看它是否可以用特殊方法（HL）来证明，最后再看一般方法是否也可以证明。

解法1：用“HL”证明Rt△BDC≌Rt△CEB。

解法2：用“SAS”证明△BDC≌△CEB。

解法3：用“AAS”证明△BDC≌△CEB。

【追问二】如图2，在例题的基础上，试证明△BOE≌△COD。

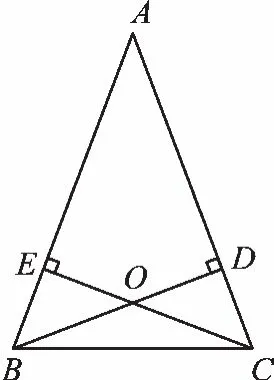
图2

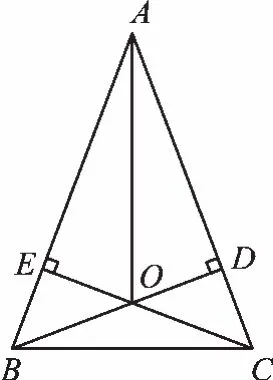
图 3

解法说明：在例题已证明结论的基础上，可用“AAS”证明△BOE≌△COD。

【追问三】如图3，在例题的基础上，试证明AO平分∠BAC。

【分析】要证明AO平分∠BAC，就是要证明∠BAO=∠CAO。我们既可以把这两个角放在△EAO、△DAO中，也可以放在△BAO、△CAO中。

证法1：用“HL”证明Rt△EAO≌Rt△DAO，推出AO平分∠BAC。

证法2：用“SSS”证明△BOA≌△COA，推出AO平分∠BAC。

【追问四】如图4，在例题的基础上，试证明AF⊥BC。

图4

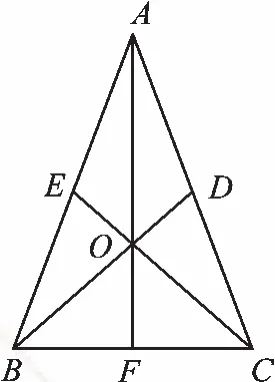
图5

证明：在△BAF和△CAF中，

【变式一】如图5，在△ABC中，AB=AC，BD、CE是中线，请问图中有几对全等三角形？如何证明？

【分析】本题应先用“SAS”证明△AEC≌△ADB，再去证明其他三角形全等。

答：七对。

【变式二】如图6，在△ABC中，AD、CE是高，AD、CE交于点O，AE=CE，试证明：AO=BC。

图6

图7

【分析】要证明结论，我们需要把问题“AO=BC”和条件“AE=CE”结合起来看，由此可以判断应该证明△AEO≌△CEB。

解法说明：应该用“同角（或等角）的余角相等”先证出∠EAO=∠ECB，然后用“ASA”证明△AEO≌△CEB，最后推出AO=BC。

【小结】本题在形式上与前面几题有所区别。我们运用“分析法”把结论和条件结合起来找出全等的两个三角形，进而运用“综合法”证明。

【变式三】如图7，∠A=∠D=90°，AB=DC，AC、BD相交于点E，找出图中相等的锐角，并加以证明。

【分析】此题是教材P36复习巩固中的第9题。从形状看，本题似乎与例题关系不大，但当延长BA、CD时，“形”就相同了。（解略）

【小结】针对一个图形，条件相同时，问题可能不同；改变条件后，结论也有可能不会改变。不同的问题起初图形不尽相同，当把它补充完整时，就会给人“神似形也似”的感觉。方法上，此题与变式一又是相同的。

【变式四】如图8，AC=BC，∠ACB=90°，D是AC上一点，AE⊥BD交BD的延长线于E，且求证：BD是∠ABC的角平分线。

图8

【分析】所给图形有点“残缺”，若延长BC、AE相交于点F，问题就变得明晰起来。

证明：在△BCD与△ACF中，

∵∠DCB=∠ACF=90°，∠F=∠BDC，AC=BC，

∴△BCD≌△ACF，∴BD=AF。

再由BE=BE，∠AEB=∠FEB，

∴△AEB≌△FEB，

∴BD平分∠ABC。

【小结】解答本题的关键是把“残缺”图形进行“完善”，使图形又与例题相类似，问题转化为寻找全等三角形。