基于PCA的数据相关性分析方法
2019-10-21 13:29徐涛
科技风 2019年19期
摘 要:主元分析(Principal component analysis,PCA)是一種经典的数据分析方法。本文将PCA方法应用于数据相关性分析中,以提取数据集变量的相关性信息。通过两个仿真实验验证了PCA方法提取数据相关性有效性。
关键词:主元分析;数据相关性
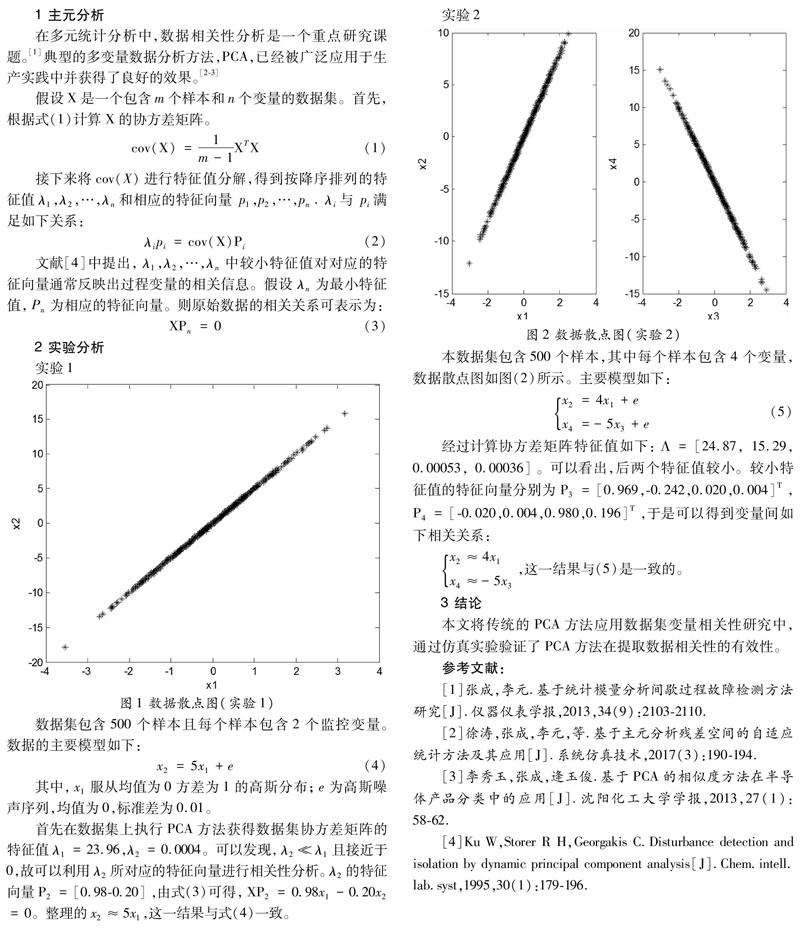
1 主元分析
在多元统计分析中,数据相关性分析是一个重点研究课题。[1]典型的多变量数据分析方法,PCA,已经被广泛应用于生产实践中并获得了良好的效果。[2-3]
3 结论
本文将传统的PCA方法应用数据集变量相关性研究中,通过仿真实验验证了PCA方法在提取数据相关性的有效性。
参考文献:
[1]张成,李元.基于统计模量分析间歇过程故障检测方法研究[J].仪器仪表学报,2013,34(9):2103-2110.
[2]徐涛,张成,李元,等.基于主元分析残差空间的自适应统计方法及其应用[J].系统仿真技术,2017(3):190-194.
[3]李秀玉,张成,逄玉俊.基于PCA的相似度方法在半导体产品分类中的应用[J].沈阳化工大学学报,2013,27(1):58-62.
[4]Ku W,Storer R H,Georgakis C.Disturbance detection and isolation by dynamic principal component analysis[J].Chem.intell.lab.syst,1995,30(1):179-196.
猜你喜欢
阅读(低年级)(2021年4期)2021-06-15
智富时代(2018年4期)2018-07-10
智富时代(2018年4期)2018-07-10
校园英语·上旬(2016年6期)2016-05-14
校园英语·上旬(2016年5期)2016-05-14
故事会(2016年4期)2016-02-19
新高考·高二数学(2014年7期)2014-09-18
福建中学数学(2011年9期)2011-11-03
三月三(2009年8期)2009-12-16
新闻爱好者(2009年14期)2009-09-18

