库水位骤降边坡渗透稳定敏感性分析

李茜莎　谭雅文

摘要：为定量研究不同非饱和参数（进气值α、土水特征曲线斜率δ、残余含水率ε、渗透系数k）对边坡渗流特性及稳定性的影响规律，利用Ceo-slope软件，基于Fredlund&Xing非饱和理论，采用灰关联度法对某土质边坡不同非饱和参数对边坡渗透稳定性的影响进行了敏感性分析。结果表明：参数α、k与浸润线高程成负相关，与位移及稳定系数成正相关;参数δ、ε与浸润线高程成正相关，而与位移及稳定系数成负相关;位移与稳定系数在库水位下降前期变化较大，而在库水位下降后期变化较小;边坡上部监测点的位移大于下部监测点的位移：对边坡稳定影响较大的参数为α与k，而参数δ与ε对边坡稳定性影响相对较小;采用灰关联度方法可直观准确地获取主要因素和次要因素，為量化研究非饱和参数对边坡稳定性的影响提供了一种方法。

关键词：灰关联度理论：非饱和参数;库水位骤降;边坡;渗透稳定;敏感性分析

中图分类号：TU432

文献标志码：A

doi：10.3969/j.issn. 1000- 1379.2019.03.029

引起库岸边坡失稳的原因主要有以下几个方面：库水位上升导致土体内部浸水引起土体强度降低、有效应力减小：库水位骤降导致边坡水压突然卸载，从而引发滑坡灾害：库水位骤降导致边坡内部水位线出现“滞后”效应[1-2]，指向边坡体外部的渗流力加剧边坡失稳。

国内外针对库水位升降情况下的边坡稳定性研究较多，如：赵瑞欣等[3]以三峡库区凉水井滑坡为例，对不同库水位升降速率以及不同饱和渗透系数下边坡稳定性进行了评价：鲁芃等[4]对白家包滑坡不同库水位日降幅条件下滑坡渗流场及应力应变进行了数值模拟：刘艺梁等[5]研究了谭家湾滑坡在不同库水位下降速率下的渗流特性以及稳定性：钟启明等[6]基于非饱和理论，计算了某黏土心墙坝在库水位骤降情况下的上游坝坡稳定系数。前人对于此类问题的研究主要集中在库水位变动速率以及饱和渗透系数大小上，而对于边坡土体本身的非饱和特性的研究较少，如刘博等[7]对某边坡非饱和特性在库水位骤降工况下的渗流特性以及边坡稳定性进行了研究，但是缺乏边坡稳定性对土体各项非饱和参数敏感性的定量研究。

边坡稳定性影响因素具有复杂性、不确定性和模糊性，通过敏感性分析，可以得到各因素影响程度排序。灰关联度法是敏感性分析方法之一，因其原理成熟、计算过程简便而被广泛应用于边坡稳定性影响因素分析[8]。笔者基于Fredlund&Xing非饱和理论[9]，选取进气值α、土水特征曲线斜率6、残余含水率ε、渗透系数k等4个土体非饱和参数，利用Geo - Slope软件中的Seep/w和Slope/w模块，采用灰关联度法对某库岸边坡的渗流特性及稳定性进行敏感性分析，以期为类似工程边坡稳定性定量化研究提供参考。

1 计算理论

1.3 边坡稳定性理论

边坡稳定性分析采用极限平衡法。传统的极限平衡法有瑞典圆弧法、Bishop法、剩余推力法以及Mor-genstern-Price法（简称M-P法）等。M-P法能够很好地揭示土条之间的相互作用力而没有作任何的简化，因此本研究采用M-P法进行滑坡体的稳定性分析。

1.4 灰关联度理论

灰关联度[14]属于灰色系统理论，在资料相对有限的情况下，可较为准确地找到影响因素值与目标影响值的联系。灰关联度分析的具体步骤如下。

1.4.1 构造比较矩阵与参考矩阵

对于边坡稳定性评价，可以选取Fredlund&Xing参数中的非饱和参数构造比较矩阵：

关联度D_i值变动区间为[0，1]。D_i值越大，表示影响因素的关联度越大，即敏感性越强。

2 实例分析

2.1 计算模型及边界条件

选择文献[7]中的计算模型进行实例分析，如图1所示，H= 14 m，h=7 m.坡比为1：2。模型初始条件为左边界obcd以及右边界gl均为13 m水头下的稳定渗流场。边界条件如下：obcd为库水位变动边界，cb边界上每一节点的水头随时间不断变化，软件每运行一步便判断节点水头是否小于节点高程，若条件成立则该节点的流量Q便被赋于0[14];ol、defg为不透水边界;gl为13 m定水头边界。模型网格如图2所示，计算全局网格尺寸约为Im，共剖分为470个节点、423个单元。

2.2 材料参数及计算工况

材料基础参数根据文献[7]取值：黏聚力c'=10kPa，内摩擦角φ'=20°，土体密度p=2 t/m3，弹性模量E=0.1 GPa，泊松比μ=0.3，库水位下降速率为1m/d，从正常蓄水位13 m下降到死水位7m，计算时间为20d，相应工况见表1。

2.3 渗流场分析

为比较库水位骤降情况下边坡土体非饱和参数变动对边坡内部浸润线的影响，图3绘出了A、B、C、D四种计算工况下库水位由13 m下降到7m时浸润线的位置。

由图3可知：不同非饱和参数对边坡内部浸润线位置有较大影响：对浸润线影响最大的参数是进气值αα值越大浸润线位置越低：其次是土体的饱和渗透系数k，k值越大浸润线位置越低，但是浸润线下降的幅度较小;参数δ与参数ε对浸润线位置影响较小，δ越大浸润线位置越高，ε越大浸润线位置也越高，但是变化幅度较小。

2.4 监测点位移分析

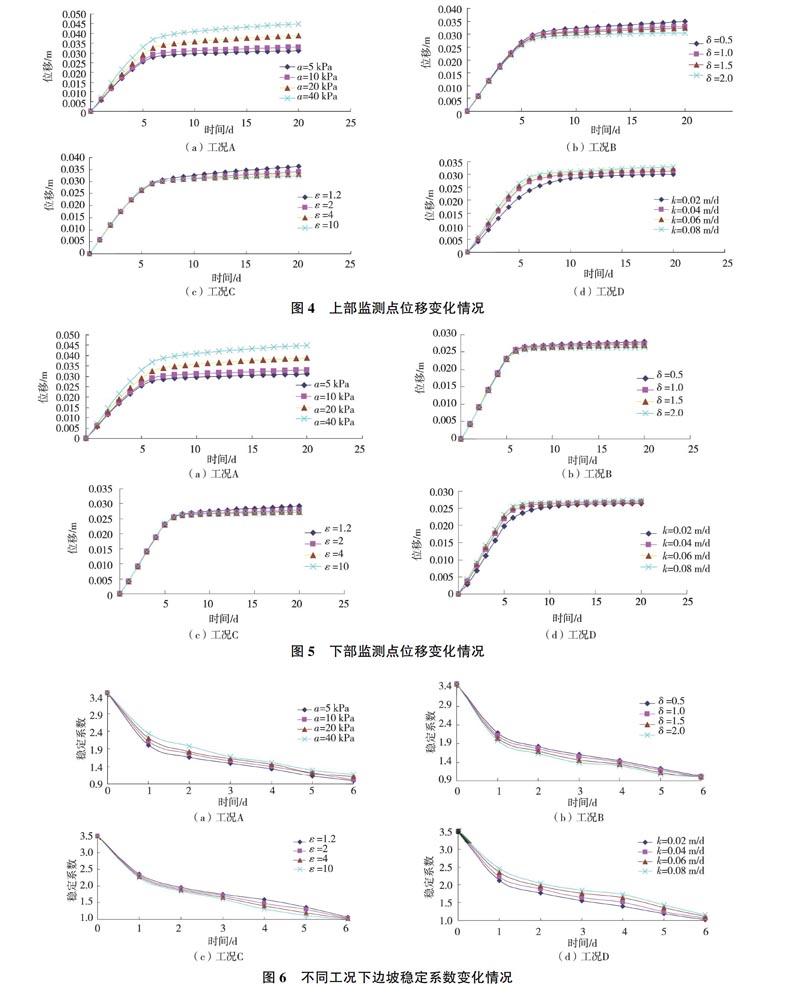
为比较不同工况下边坡上部与下部位移变化情况，选取图1所示两个监测点进行分析，不同工况下不同监测点位移变化情况见图4、图5。

总体上来看，边坡上部监测点与下部监测点的位移变化趋势类似，在库水位下降过程中位移变化较大，而在库水位下降后仍然存在一定的位移，但是位移较小。在库水位骤降情况下，参数α对边坡位移的影响最大，α取不同值时上部监测点的最大位移为3.11 -4.48 cm，下部监测点的最大位移为2.67 -4.34 cm;参数δ、ε、k对边坡位移影响相对较小，在工况B、C、D情况下上部监测点的位移为3.01-3.63 cm.而下部监测点的位移在2.63 -2.92 cm之间。可见参数α对边坡稳定性的影响大于参数δ、ε、k对边坡稳定性的影响。同时还可以看出，在库水位骤降工况下，边坡上部监测点的位移大于下部监测点的位移。