数学“难题”解答过程中的思路引领

姜仁玲

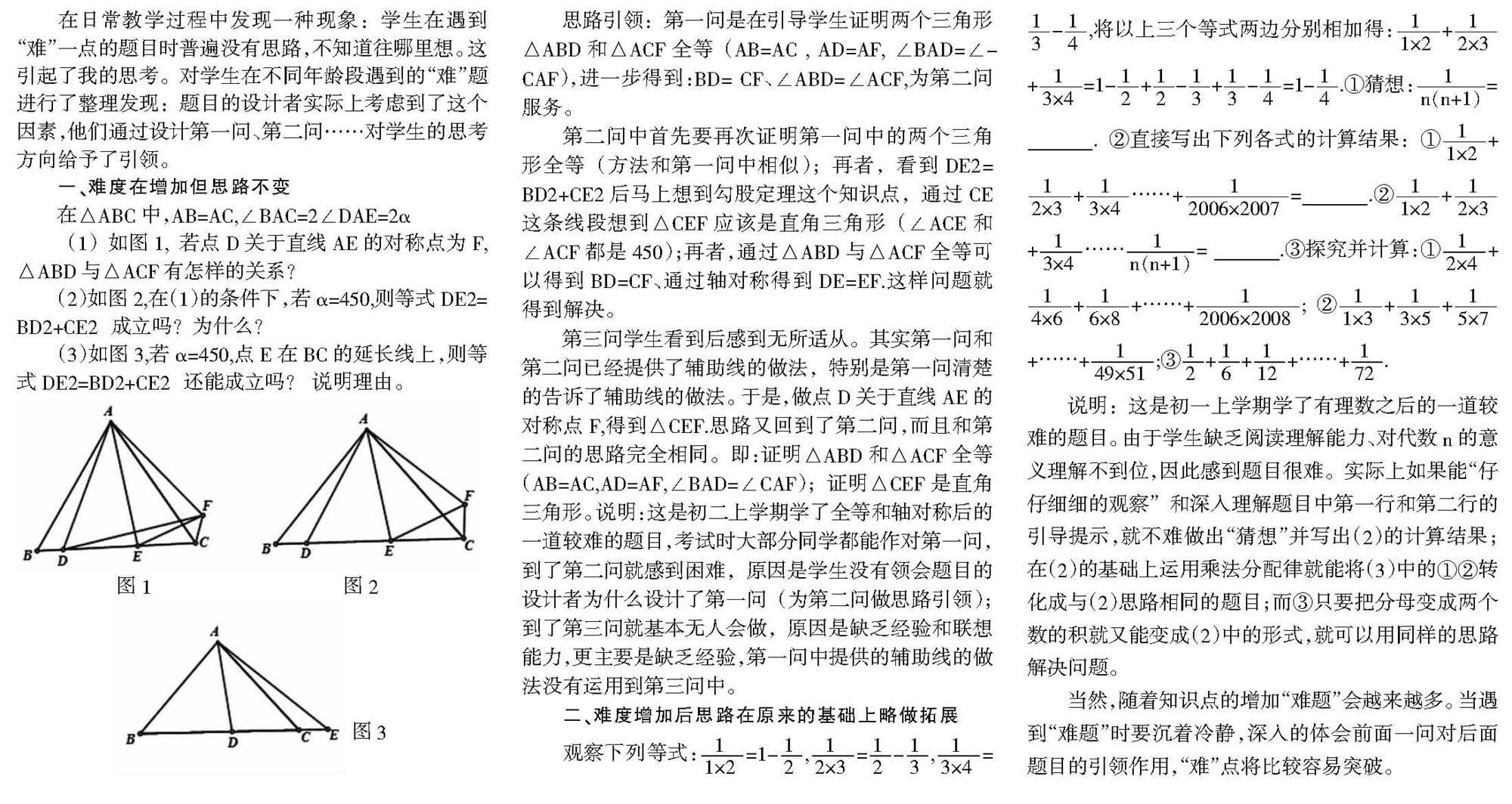
在日常教学过程中发现一种现象：学生在遇到“难”一点的题目时普遍没有思路，不知道往哪里想。这引起了我的思考。对学生在不同年龄段遇到的“难”题进行了整理发现：题目的设计者实际上考虑到了这个因素，他们通过设计第一问、第二问……对学生的思考方向给予了引领。

一、难度在增加但思路不变

在△ABC中，AB=AC，∠BAC=2∠DAE=2α

（1）如图1，若点D关于直线AE的对称点为F，△ABD与△ACF有怎样的关系？

（2）如图2，在（1）的条件下，若α=45⁰，则等式DE²=BD²+CE²成立吗？为什么？

（3）如图3，若α=45⁰，点E在BC的延长线上，则等式DE²=BD²+CE²还能成立吗？ 说明理由。

思路引领：第一问是在引导学生证明两个三角形△ABD和△ACF全等（AB=AC ， AD=AF， ∠BAD=∠CAF），进一步得到：BD= CF、∠ABD=∠ACF，为第二问服务。

第二问中首先要再次证明第一问中的两个三角形全等（方法和第一问中相似）;再者，看到DE²=BD²+CE²后马上想到勾股定理这个知识点，通过CE这条线段想到△CEF应该是直角三角形（∠ACE和∠ACF都是45⁰）;再者，通过△ABD与△ACF全等可以得到BD=CF、通过轴对称得到DE=EF。这样问题就得到解決。

第三问学生看到后感到无所适从。其实第一问和第二问已经提供了辅助线的做法，特别是第一问清楚的告诉了辅助线的做法。于是，做点D关于直线AE的对称点F，得到△CEF。思路又回到了第二问，而且和第二问的思路完全相同。即：证明△ABD和△ACF全等（AB=AC，AD=AF，∠BAD=∠CAF）;证明△CEF是直角三角形。说明：这是初二上学期学了全等和轴对称后的一道较难的题目，考试时大部分同学都能作对第一问，到了第二问就感到困难，原因是学生没有领会题目的设计者为什么设计了第一问（为第二问做思路引领）;到了第三问就基本无人会做，原因是缺乏经验和联想能力，更主要是缺乏经验，第一问中提供的辅助线的做法没有运用到第三问中。

二、难度增加后思路在原来的基础上略做拓展

说明：这是初一上学期学了有理数之后的一道较难的题目。由于学生缺乏阅读理解能力、对代数n的意义理解不到位，因此感到题目很难。实际上如果能“仔仔细细的观察”和深入理解题目中第一行和第二行的引导提示，就不难做出“猜想”并写出（2）的计算结果;在（2）的基础上运用乘法分配律就能将（3）中的①②转化成与（2）思路相同的题目;而③只要把分母变成两个数的积就又能变成（2）中的形式，就可以用同样的思路解决问题。

当然，随着知识点的增加“难题”会越来越多。当遇到“难题”时要沉着冷静，深入的体会前面一问对后面题目的引领作用，“难”点将比较容易突破。