关于区间数绝对值运算的几个结果

覃小莉,KHALIL Ahmed,张 琛,李生刚

(1.陕西师范大学 数学与信息科学学院,陕西 西安 710062;2.成都师范学院 德阳高级中学,四川 德阳 618000;3.陇东学院 数学与统计学院,甘肃 庆阳 745000)

1 引言及预备知识

区间数的理论和应用在建立区间值微分方程理论[1], 区间值最优化理论[2]以及模糊值函数的微分理论[3]中有着重要地位, 所以清楚区间数的性质有很重要的意义。 一些学者对区间数做了不少的研究, 丰富了区间数的理论知识[4-6]。区间数理论的基本思想是应用区间数变量代替点变量进行计算,所以在应用问题[4-10]中区间数经常被使用。 文献[11]研究了区间数绝对值的性质, 但是对于区间数的四则运算没有进行仔细的讨论。文献[12-13]研究了区间数的特殊值-模糊值相关问题, 但是对于区间数的一般值没有研究。本文借助数的四则运算和一元运算的一般概念, 讨论了区间数相关性质并定义一种新的区间数绝对值运算。

(1) 加法

(2) 减法

减法也可以定义为

(3) 乘法

乘法也可以定义为

(4) 除法

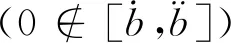
除法也可以定义为

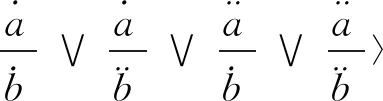
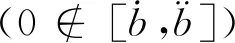
文献[11]定义了区间数的一种绝对值运算:

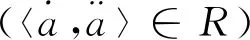
该作者证明了这种绝对值运算具有许多良好性质。 本文将定义区间数的另一种绝对值运算:

2 主要结果

定理1R上的绝对值运算(|·|和‖·‖)及四则运算有下列性质:

成立；在其余情形,即(ⅴ)～(ⅷ)之一时不等式

成立。

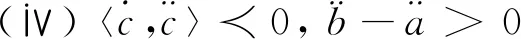
(11) |[a*⊖b*]c|≤[‖a*⊖b*‖]c。

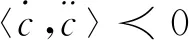
(16) [(a*⊙b*)⊕(a*⊙c*)]c=[a*⊙(b*⊕c*)]c。

(17) 当a*,b*,c*同号时, 有a*⊙(b*⊕c*)=(a*⊙b*)⊕(a*⊙c*)。

其余结论显然成立。

(2) 考虑以下4种情形。

(3) 由(2)和(1)知

(4) 由(1)知，k1k2=0时等式成立。当k1>0且k2>0时，

同理可证当k1<0且k2<0时等式成立。

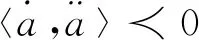
(7)k1k2=0时,等式显然成立。设k1k2≠0,分4种情形讨论。

即等式是成立的。

即等式是成立的。

若k1>0且k2<0,则

即k1<0且k2>0时等式也是成立的。

若k1>0且k2<0,则

即k1<0且k2>0时等式也是成立的。

(10) 由减法和绝对值的定义可以得到等式

及

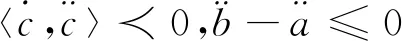
(11) 事实上,由定义得

[‖a*⊖b*‖]c

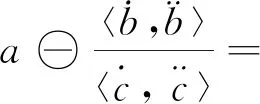
(16) 由

[(a*⊙b*)⊕(a*⊙c*)]c=

和

[a*⊙(b*⊕c*)]c=

知

[(a*⊙b*)⊕(a*⊙c*)]c=[a*⊙(b*⊕c*)]c

(17) 当a*≻0,b*≻0,c*≻0 时,有

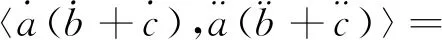
而

即

a*⊙(b*⊕c*)=a*⊙b*⊕a*⊙c*

当a*0,b*0,c*0 时, 有

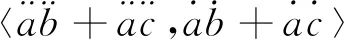
而

即

a*⊙(b*⊕c*)=a*⊙b*⊕a*⊙c*

注1等式

和