厚板坯连铸中间包流场优化

张立夫，王鲁毅，崔福祥，吕春风，张宏亮，张晓光

（1.鞍钢股份有限公司鲅鱼圈钢铁分公司，辽宁 营口 115007；2.鞍钢集团钢铁研究院，辽宁 鞍山 114009）

中间包内流体流动状态及速度分布对流体成分和温度的均匀性、夹杂物的上浮与排除有着重要的影响，而中间包及其控流装置的结构决定了中间包内流体的流动状态与速度分布[1]。因此，深入了解和控制钢液在中间包内的流动行为是保证中间包冶金效果和提高钢液质量的关键。鞍钢股份有限公司鲅鱼圈炼钢部在生产过程中出现部分钢种探伤合格率低的问题，分析后认为是夹杂物导致，夹杂物组分分析表明疑似中包渣，而中间包流场不合理容易导致卷渣事件发生。为降低并控制由中间包流场原因导致的夹杂物缺陷风险，利用数值模拟和水模实验，对比分析了4种中间包控流装置方案的特点，以确定合理的中间包控流装置，有效控制中间包内钢水的夹杂物。

1 数学模型计算

以2 300 mm×300 mm的单流大断面板坯中间包为研究对象，设计了4种控流装置方案，图1为控流装置方案示意图，表1为方案说明。模拟工艺参数见表2。为保证计算的完整和真实，以整个中间包流场区域作为建模范围,而且全部采用六面体结构化网格以保证计算精度。

1.1 模型基本假设

模型基本假设如下：

（1）中间包内钢液流动为粘性不可压缩流动；

图1 控流装置方案示意图

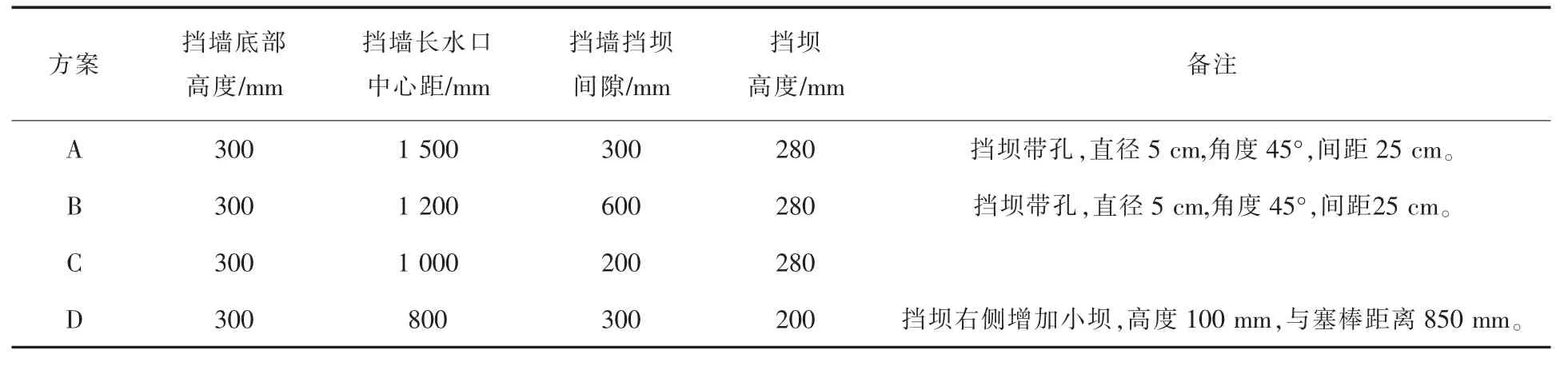
表1 方案说明

表2 模拟工艺参数

（2）中间包内钢液为湍流流动；

（3）中间包内钢液为稳态过程；

（4）忽略表面渣层和液面波动的影响；

（5）计算出稳态流场后，在非稳态下求解示踪剂扩散方程，计算示踪剂浓度随时间的变化规律，得到RTD（钢水在中间包内停留时间）曲线。

1.2 控制方程

中间包内钢水流动行为可用连续性方程、动量方程（N-S方程）及标准k-ε双方程来描述。其中，标准k-ε双方程模型由湍流动能k方程及其耗散率ε方程描述。各方程的具体形式如下所述：

（1）连续性方程：

（2） 动量方程（N-S 方程）:

（3）湍流动能k方程：

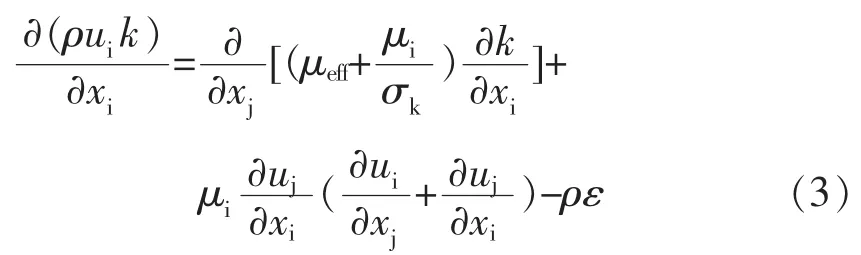
（4）湍流动能耗散率ε方程：

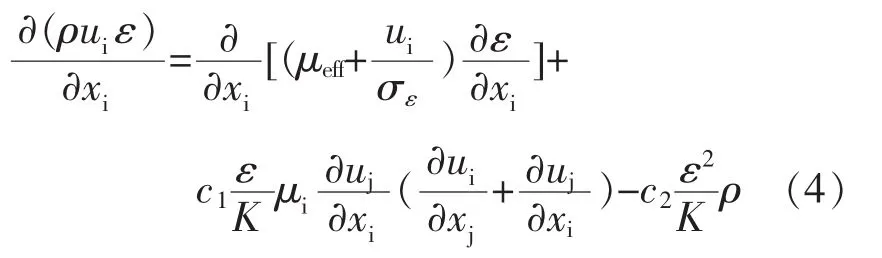
以上各式中,ui、uj为速度矢量，m/s； μ 为层流粘度，Pa·s;k 为湍动能，m2/s2;xi、xj为方向矢量，m;μi为湍流粘度，Pa·s；ε 为湍动能耗散率，m2/s2;ρ为流体密度，kg/m3;μeff为有效粘度，Pa·s。

表3为k-ε模型中常数值。为得到RTD曲线，根据刺激—响应原理，从某时刻起向中间包内注入示踪剂1 s，并在出口实时监控示踪剂的浓度变化规律。示踪剂扩散方程为：

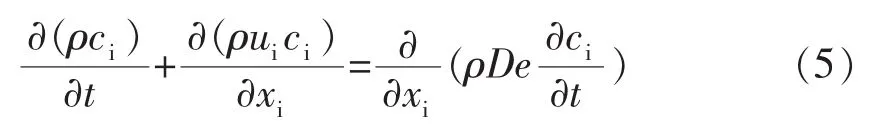
表3 模型中常数值

1.3 边界条件

边界条件如下：

（1）自由表面：忽略表面渣层影响，所有变量的垂直梯度均为零，垂直于自由表面的速度分量为零。

（2）入口：入口边界设置为流量入口，假设入口截面上速度分布相同且垂直向下，速度大小根据实际中间包通钢量计算。

（3）出口：出口设定为自由流出边界条件。

（4）壁面：采用无滑移边界条件，壁面附近流场采用标准壁面函数计算。各壁面散热量取Sahai推荐值[2]，即自由液面、中间包底部、中间包纵向壁面和横向包壁的热通量分别取 15、1.4、3.2和3.8 kW/m3。

2 结果与分析

本研究对中间包三维流场进行数值模拟计算，得到稳态的流场后，在钢液入口处加入示踪剂1 s，求解示踪剂三维湍流传质扩散方程，进行瞬态解2 000 s，得到钢液在中间包出口的浓度随时间的分布情况。

2.1 不同方案下的流场对比分析

控流方案A、B、C、D条件下中间包内流线轨迹图如图2，流线单位为m/s。

图2 中间包内流线轨迹图

从图2中可以看出，在A方案的条件下，由于挡墙离塞棒比较近，钢水过挡墙后在浇注区行程比较短，而且容易造成中间包钢水液面的扰动，按B、C、D的顺序，挡墙和坝不断向长水口侧移动，冲击区不断变小，浇注区不断变大，钢水在浇注区的行程不断增加，主流股倾向于在中间包中上层，有利于夹杂物的排除。

2.2 不同方案下的RTD曲线分析

中间包流体流动的体积可划分为活塞流体积、死区体积和混合流体积，死区体积越小，越有利于中间包冶金作用的发挥。中间包内钢液平均停留时间越长，越有利于夹杂物的上浮[4]。图3为各方案的RTD曲线，根据RTD曲线计算平均停留时间、死区比例、混合流比例及活塞流比例，表4为数模中RTD曲线计算及分析结果。

对比4个方案发现，RTD曲线趋势大致相似，但计算结果有所差异。从钢水平均停留时间角度看，方案D与方案A相当；从死区比例来看，B、C、D方案比方案A均有所减小，其中方案B最小。综合结果认为，方案D明显优于方案A。

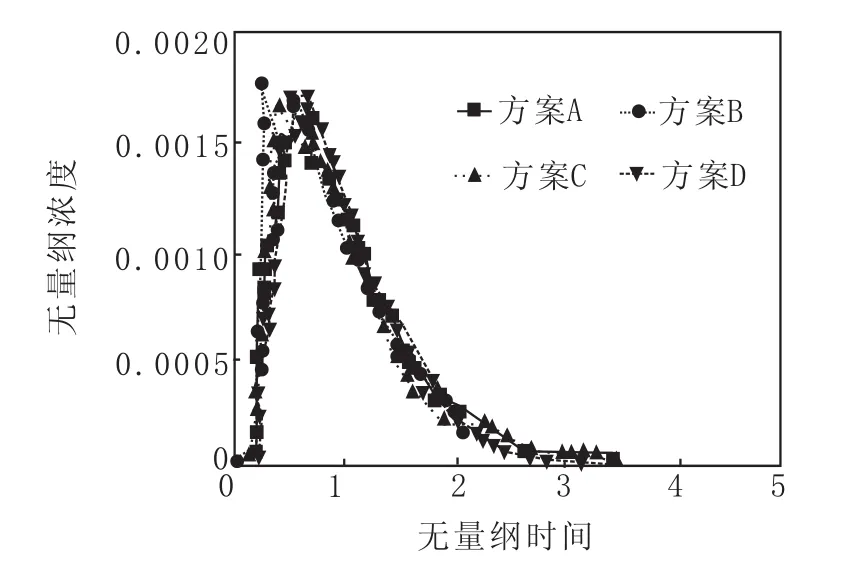
图3 各方案RTD曲线

表4 RTD曲线计算及分析结果

3 水模实验分析

为验证数模计算结论的准确性，以中间包为原型，进行水模验证实验。模型按与实物1∶3的比例采用有机玻璃制成，以水代替钢液，中间包水模试验流程简图见图4。

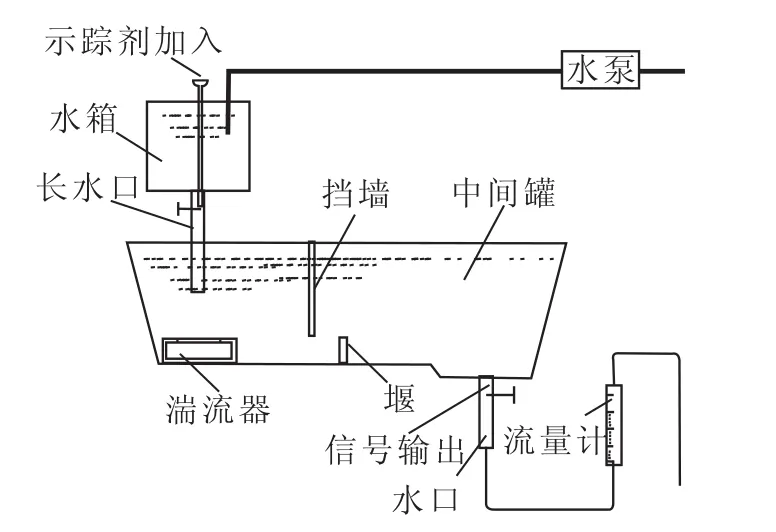
图4 中间包水模试验流程简图

中间包内钢液的流动一般可视为粘性不可压缩稳态等温流动。模拟实验选用水作为介质。要保证与重力有关的弗鲁德数相等即可。相应的模型与原型的关系为：

以上各式中,Lm为模型特征长度，m；Ls为原型特征长度，m；um为模型流体速度，m/s；us为原型流体速度，m/s；Qm为模型的流量，m3/h；Qs为原型的流量，m3/h；tm为模型的时间，s；ts为原型的时间，s。

本实验用电导率仪测定中间包内液体停留时间分布。选择饱和浓度的KCl溶液300 ml加入钢包至中间包的流股中，在中间包下出口处用电导仪测量液体中KCl浓度随时间的变化情况，用记录仪绘出其变化的函数曲线，记录示踪剂在中间包出口处响应的时间、浓度达到最大时的时间，通过计算得出平均停留时间ta，计算公式如下：

式中，C为KCl溶液浓度，t为时间。

表5为水模实验RTD曲线计算及分析结果。从表5可看出，方案D条件下，死区比例有所减小，活塞区比例显著增大。

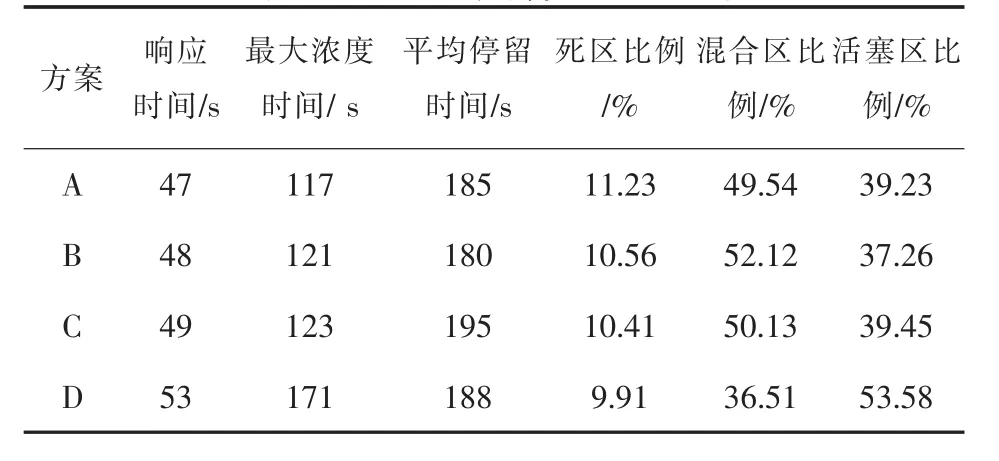
表5 RTD曲线计算及分析结果

为测量中间包液面流速情况，在中间包液面播撒聚苯乙烯塑料粒子，对不同工况的中间包液面流动情况进行了录像。经对录像截图分析，计算液面某点的流动速度，以此反映中间包挡墙设置对液面的影响，表6为中间包液面测速结果。

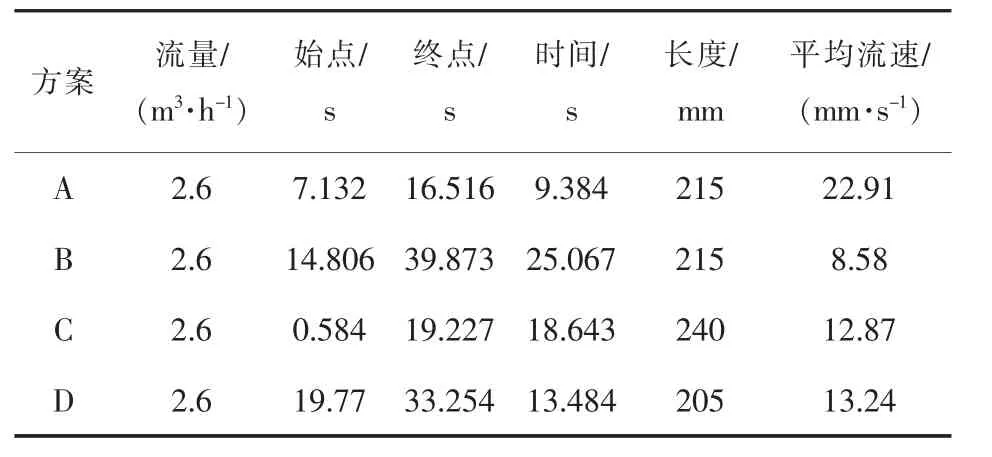
表6 中间包液面测速结果

由表6看出，A挡墙设置方案平均速度最大，表明出口区钢液流动对液面冲击激烈，不利于结晶器的稳定浇注。其余3种方案条件下液面流速均显著减小。

4 方案实施情况

根据计算和水模实验评价结果选择方案D作为实施方案，应用于管线钢生产中，共11个浇次。抽取铸坯试样进行夹杂物扫描和统计，结果是夹杂物尺寸多分布在0～3 μm，经计算比例为68.76%，其余为 3～10 μm，没发现大于 10 μm 的夹杂物。典型夹杂物形貌及能谱图见图5。由图5看出，夹杂为精炼处理常见夹杂类型，不是卷渣产物。方案实施后的管线钢探伤合格率为98.6%，比原来提高了0.9%，夹杂物控制得到改善。

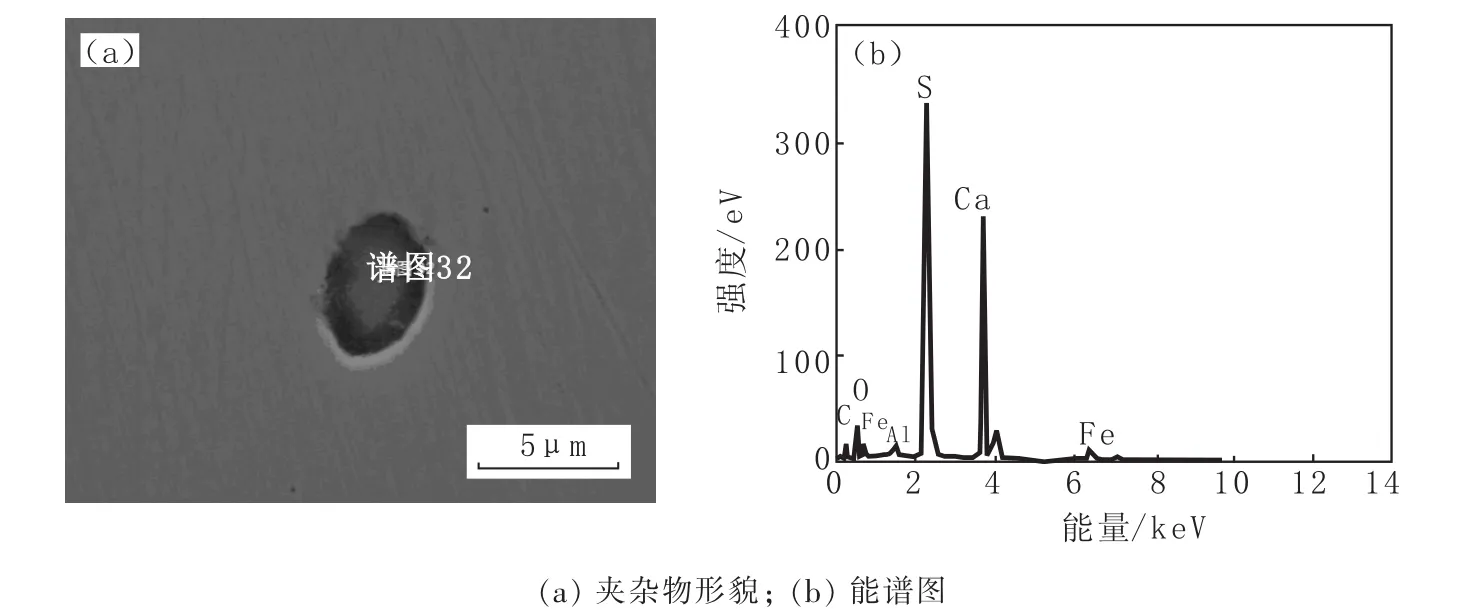
图5 典型夹杂物形貌及能谱图

5 结论

（1） 对 4 种中间包挡墙设置方案（A、B、C、D）的数值模拟和水模实验结果表明，方案D的中间包挡墙和挡坝向长水口侧移动后，钢水冲击区显著减小，浇注区显著增大，钢水在浇注区的行程不断增加，主流股倾向于在中间包中上层，死区比例小、钢液平均停留时间长，有利于夹杂物的排除。

（2）方案D应用于管线钢生产后，管线钢探伤合格率比原来提高了0.9%，夹杂物缺陷得到改善。