变频空调器最大APF指标的快速求解方法
(上海交通大学制冷与低温工程研究所 上海 200240)
变频空调器具有高效、节能和舒适的优点,已发展成家用空调器市场的主导产品[1]。变频空调器能效采用APF指标衡量,其计算式由GB/T 7725—2004规定[2]。变频空调器APF由额定制冷、中间制冷、额定制热、中间制热和低温制热5个工况下的能力、能效值计算得到,是一个具有10个自变量的函数[3-4]。APF定义式由国家标准中的隐式表达式给出。APF各个变量之间存在相互关系,使APF最大值无法直接从APF定义式中获得[5]。
目前主要采用多次重复实验的方法来获得空调器最大APF[6-7],进行多次空调器的整机实验,直至APF达到最大值[8-9]。获得一个APF需要实验测得5个工况的能力和能效数据,所以通过多次重复实验获得最大APF的方法所需的总实验次数极大。此外,该方法得到的最大APF是有限工况点下的最大APF,并非理论上的APF全局最大值。
采用系统仿真方法获得最大APF可以减少实验次数,但仍需大量实验数据进行精度验证[10-11]。系统仿真方法是通过国标性能约束和几何尺寸约束建立空调整机模型,并进行多次空调器的系统仿真,直至APF达到最大值。空调器在APF 5个测试工况下的运行特性差异很大,如环境温度、蒸发温度、冷凝温度、压缩机的压缩比[12-13],导致空调器整机模型精度验证十分复杂。
目前还没有一种简单快速地求解变频空调器最大APF的方法。快速求解空调器的最大APF存在两个困难:1)国标中APF定义式是隐式的,无法直接用优化算法求解最大APF;2)空调器5个工况之间存在相互联系,能力和能效的值也受到约束,将每个工况单独匹配到最优并不能使APF最大[14-15]。
本文提出一种多约束条件下的寻优方法,可快速求解出最大APF。
1 快速求解最大APF的方法
快速求解APF最大值的思路是以APF公式作为目标函数,以国标性能约束和几何尺寸约束作为约束方程,采用多约束条件寻优法求解。
快速求解APF最大值的步骤如下:1)将国标中复杂的APF隐式定义式转化为简单的APF显示计算公式;2)根据国标中的限制和空调器几何尺寸的约束,推导APF各个自变量的相互约束方程;3)联立目标函数与约束条件,采用多约束条件寻优法求解得到APF最大值,如式(1)、式(2)所示。
APFmax=f(φcr,φcm,φhr,φhm,φdef,EERcr,EERcm,COPhr,COPhm,COPdef)
(1)
(2)
2 APF目标函数显式公式推导
为提升APF的计算速度,首先需要解决隐式方程迭代计算速度过慢的问题,需要将APF的原始隐式定义式转化为显式公式;其次应尽可能简化表达式,以进一步提升计算速度。
2.1 国标中的APF隐式定义式
APF是指空调器在制冷季节和制热季节期间,从室内空气中除去的冷量与送入室内热量的总和与同期间内消耗电量的总和之比,定义式由GB/T 7725—2004给出,如式(3)所示。CSTL为制冷季节总负荷,Wh;HSTL为制热季节总负荷,Wh;CSTE为制冷季节耗电量,Wh;HSTE为制热季节耗电量,Wh。这4个变量的定义分别由式(4)~式(7)确定,计算过程中的其余变量由GB/T 7725—2004给出。
(3)
(4)
(5)
(6)
(7)
式中:tj为室外温度,℃;nj为各个室外温度的小时数,h;φcr2(tj)为空调器的制冷能力,W;Pc2为额定耗电量,W;BLc(tj)为建筑冷负荷,W;BLh(tj)为建筑热负荷,W;Ph(tj)为制热运行耗电量,W;PRH(tj)为辅助电加热量,W。
2.2 APF隐式公式的显式化推导
根据国家标准定义的APF计算方法,需要利用大量公式,非常繁杂。其中CSTL、HSTL、CSTE和HSTE的表达式是隐式的,计算中需要反复迭代,增加了计算量。因此需要将APF的隐式定义式转化为显式计算式。
转换成显式计算式的思路是,先通过消元将APF计算式中的隐式变量CSTL、HSTL、CSTE和HSTL分别推导为显式表达式,然后将这些显式表达式带入APF定义式。
转换过程主要步骤为:将国标中φcr2(tj)和BLc(tj)的公式代入式(4),得到CSTE关于额定制冷量的函数,如式(8)所示;将国标中BLh(tj)的公式代入式(5),得到HSTL关于额定制冷量的函数,如式(9)所示;将国标中Pclm(tj)、Pcm2(tj)和Pc2(tj)的公式代入式(6),得到CSTE的显式公式,如式(10)所示;将国标中Ph(tj)、PRH(tj)的公式代入式(7),得到HSTE的显式公式,如式(11)所示。
CSTL=626.67φcr
(8)
HSTL=368.29φcr
(9)

(10)
(11)
最后将式(8)~式(11)带入式(3),得到APF的显式表达式,如式(12)所示。
APF=991.29φcr2/(CSTE+HSTE)
(12)
2.3 APF显式计算式简化
由式(12)给出的APF显式计算式,虽然比式(3)~式(7)组成的隐式计算式简单,但其中CSTE和HSTE的表达式仍较复杂,还需进一步简化。
2.3.1 APF显式计算简化的思路
简化的思路是首先将形式复杂的变量CSTE和HSTE进行拟合,得到形式简单的CSTEfit和HSTEfit,然后将CSTEfit和HSTEfit代入APF显式计算式,得到简单的APF计算式。
2.3.2 变量CSTE的拟合
变量CSTE的拟合步骤如下:
1)根据CSTE的自变量的形式确定CSTEfit的拟合形式。CSTE的自变量包括EERcr2/EERcrm和Pc2。CSTE与Pc2成正比,且与EERcr2/EERcrm的关系接近线性,如图1所示,即CSTE/Pc2可以拟合成EERcr2/EERcrm的线性函数。
2)确定空调器各个自变量的变化范围。通过调研常用机型空调器的参数,EERcr2/EERcrm的变化范围为0.6~1.0[16]。
3)利用数据点进行拟合,确定公式中的拟合系数,拟合结果如式(13)所示。

(13)

图1 CSTE/Pc2在不同自变量下的取值Fig.1 Variation of CSTE/Pc2 with EERcr/EERcm
2.3.3 变量HSTE的拟合
变量HSTE的拟合步骤如下:
1)根据HSTE自变量的形式确定HSTEfit拟合形式。HSTE的自变量包括Phr、Phm、Pdef、φhr/φcr2、φdef/φcr2。HSTE是关于变量Phr、Phm、Pdef的线性函数;Pdef的系数可用φhr/φcr2、φdef/φcr2的二次多项式进行拟合;Phr和Phm的系数可用φhr/φcr2的二次多项式进行拟合。
2)确定空调器各个自变量的变化范围。通过调研常用机型空调器的参数,φdef/φcr2的变化范围为1.0~1.4,φhr/φcr2的变化范围为1.0~1.4,Phr的变化范围为600~1 400 W,Pdef的变化范围为1 300~1 600 W[16]。
3)利用数据点进行拟合,确定公式中的拟合系数,拟合结果如式(14)所示。
2.3.4 显式计算的APF简化公式
最后将CSTEfit和HSTEfit的计算式(13)和(14)代入式(12),得到APF显式计算的简化公式(15)。

(14)
(15)
2.4 APF显式计算公式误差分析
简化后的APF显式计算式的误差来源于变量CSTEfit和HSTEfit的近似拟合。
变量CSTEfit最大拟合误差由式(16)计算。在常用空调器参数范围内[16],计算出当EERcr2/EERcrm=0.6时,CSTEfit的误差最大,最大误差为0.45%。
(16)
HSTEfit的最大拟合误差由式(17)计算。在常用空调器的参数范围内[16],计算可得,在φdef/φcr2=1.18,φhr/φcr2=1.31,Phr=1 323 W,Phm=461 W,Pdef=1 538 W时,误差最大,最大误差为0.2%。
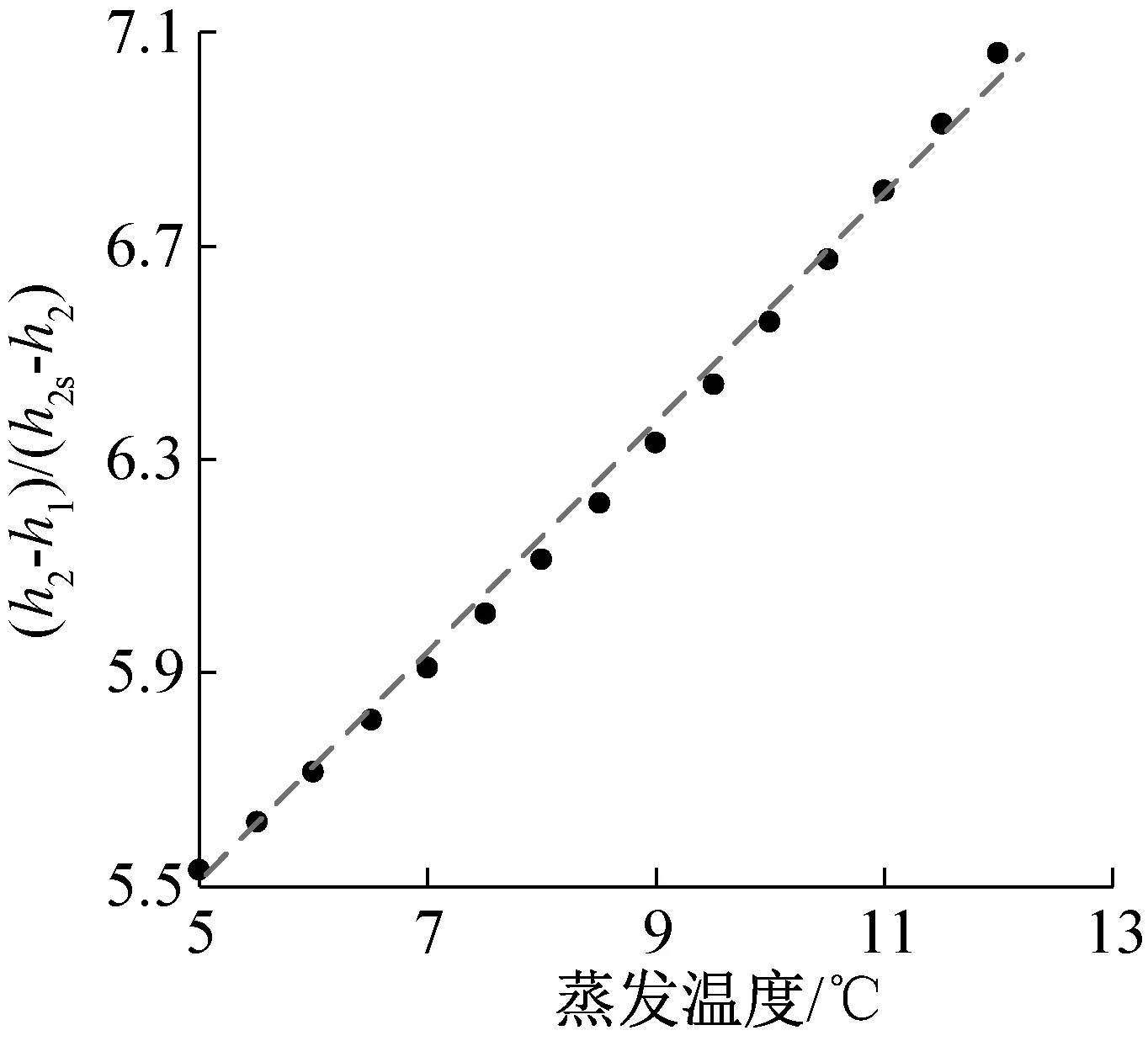
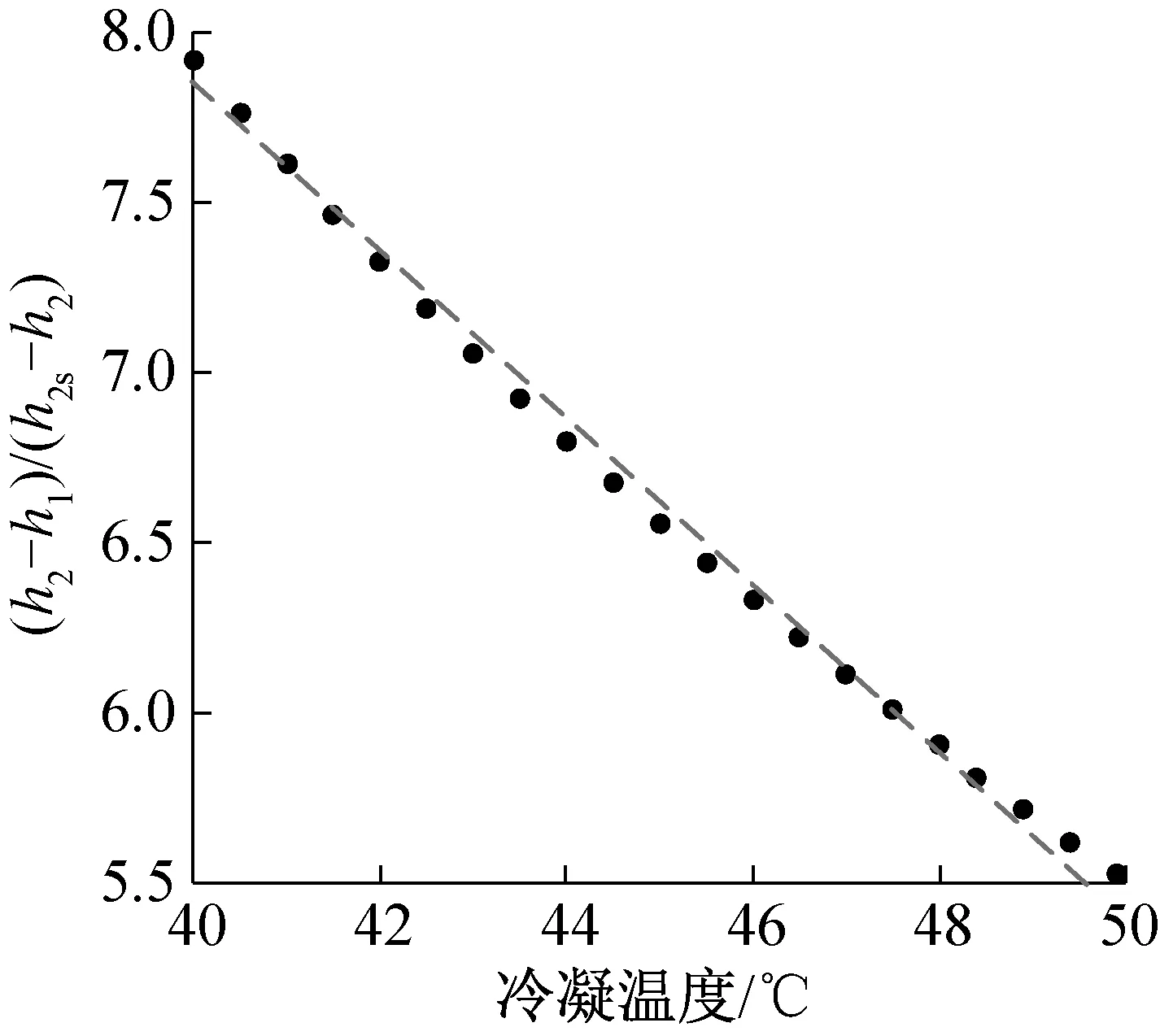
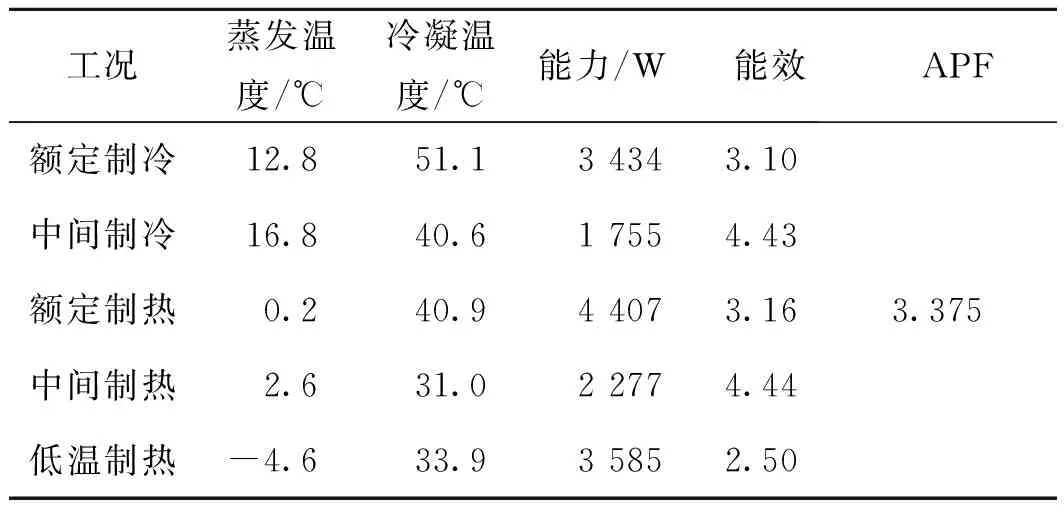
APF显式计算式的误差由式(18)计算,变量CSTEfit和HSTEfit是APFfit分母的一部分,APF近似计算误差 (17) (18) APF有两类约束方程,分别为能力约束方程和能效约束方程;能力约束方程来自国标性能约束,能效约束方程来自几何尺寸约束。GB/T 7725—2004规定了关于额定工况能力和半工况能力的约束关系。空调换热器的几何尺寸约束了空调器在5个测试工况下的能效。 为了满足国标的规定和空调器结构参数的要求,需要将上述两类约束条件转化成约束方程,作为APF目标函数优化求解的约束条件。 能力约束方程来自国标性能约束。GB/T 7725—2004规定,中间制冷能力是额定制冷能力的一半,如式(19)所示;中间制热能力是额定制热能力的一半,如式(20)所示。 φcm=0.5φcr (19) φhm=0.5φhr (20) 3.3.1 理论推导 空调器在APF 5个测试工况下运行时,空调换热器的几何尺寸是不变的,所以空调器在5个测试工况下的能效值是受到约束的。 能效约束方程就是通过换热器的几何尺寸约束推导得到的。理论循环示意图如图2所示,能效值可表示为室内机进出口的制冷剂焓差与压缩机进出口制冷剂焓差的比值,如式(21)所示。式中(h2-h1)/(h2s-h2)的值只与蒸发温度Te、冷凝温度Tc有关,且与Te和Tc的关系接近线性,运用数据拟合的方法可将变量(h2-h1)/(h2s-h2)简化为Te和Tc的线性函数,如图3、图4所示。蒸发温度或冷凝温度可表示为室内机的UA与换热量的函数,如式(22)所示。其中UA主要由空气侧的热阻决定,可近似视为定值。UA的值可通过实验测得的蒸发温度或冷凝温度和对应的能力值计算,如式(23)所示。将式(22)、式(23)带入式(21),得到测试工况能效的约束方程,如式(24)所示。 图2 理论循环示意图Fig.2 Diagram of the theoretical cycle 图3 不同蒸发温度下变量(h2-h1)/(h2s-h2)的值Fig.3 Variation of (h2-h1)/(h2s-h2)with evaporating temperature 图4 不同冷凝温度下变量(h2-h1)/(h2s-h2)的值Fig.4 Variation of (h2-h1)/(h2s-h2)with condensing temperature (21) Tindoor=Tair,indoor-φ/UA (22) (23) EER=k[a+b(Tair,indoor- (24) 式中:k为压缩机等熵压缩效率;EER为理论循环的能效;h1、h2、h2s为循环各点的焓,kJ/kg;Te为蒸发温度,℃;Tc为冷凝温度,℃;a、b、c为拟合系数;Tair,indoor为室内空气干球温度,℃;Tindoor为室内机的蒸发或冷凝温度,℃;UA为室内机的换热系数,kJ/K;φ为制冷量或制热量,W;Texp为实验测得的蒸发或冷凝温度,℃;φexp为实验测得的能力值,W。 采用上述方法,可以分别得到额定制冷、中间制冷、额定制热、中间制热和低温制热5个工况能效的约束方程,分别如式(25a)~式(25e)所示。 (25) 3.3.2 误差分析 能效约束方程的误差由能效与蒸发温度和冷凝温度之间的近似拟合导致,由式(26)计算。对于制冷剂R410A,拟合系数a=13.121 2、b=0.189 0、c=-0.194 9,常用空调器蒸发温度范围为5~12 ℃,冷凝温度范围为40~50 ℃。根据式(26)计算可得,在蒸发温度为12 ℃,冷凝温度为45 ℃时误差最大,最大误差为0.42%。 (26) APF最大值采用多约束条件寻优进行求解。多约束条件寻优以APF显式公式为目标函数,基于能力约束方程和能效约束方程,运用遗传算法求解最优值。多约束条件寻优过程如下: 1)将额定制冷、额定制热和低温制热能力组合作为个体初始化种群G0。 2)根据APF约束方程计算个体特征参数。 3)利用APF目标函数计算每个个体的APF,若个体APF增大,转至第4步;否则选取APF最大的个体参数作为最终求解结果,迭代终止。 4)在Gn代种群中挑选出适应度高的个体组成下一代种群Gn+1,Gn+1代种群发生遗传变异产生子代Pn+1,转至步骤2。 5)重复步骤2~4,直到产生APF的最大值和各个测试工况性能值。 本文选择了一款常用的变频空调器进行APF最大值求解。空调器的输入参数包括一组实验数据,包括额定制冷、中间制冷、额定制热、中间制热和低温制热5个工况点的蒸发温度、冷凝温度、能力和能效值,如表1所示。 表1 常用房间空调器各工况点测试数据Tab.1 Testing data of a commonly used room air conditioner 采用多约束寻优方法求解APF最大值,目标函数是APF显式计算式,如式(15)所示;约束方程由式(19)、式(20)和式(25)给出,式中参数由表1中的数据确定;寻优算法是遗传算法,可以直接使用MATLAB optimtool工具箱中提供的遗传算法。具体步骤如下: 目标函数:APF显式计算公式,式(15); 约束条件: 求解工具:MATLAB optimal工具箱中遗传算法。 APF最大值的求解结果如表2所示。通过计算结果可知,该型号变频空调器需要适当降低额定制冷和中间制冷工况的能力以提高能效,而额定制热、中间制热和低温制热工况需要提升能力,能效可以适当降低。优化后该变频空调器的APF与原测试值相比提升了6.37%。 表2 房间空调器最大APF及各工况性能Tab.2 Maximum APF and detailed capacities and powers of air conditioner 1)本文提出一种快速求解变频空调器最大APF的方法。该方法首先将国标中复杂的APF隐式定义转化为简单的APF显式计算式,作为优化计算的目标函数;根据国标规定和空调器结构参数的限制,得到优化计算的约束方程;通过优化计算得到变频空调APF的最大值和对应5个工况能力能效组合。 2)根据GB/T 7725—2004中APF的隐式定义式,推导了APF的显式公式并进行了简化,得到了形式简单的APF显式公式,其计算误差在常用空调器性能数值范围内<0.65%。 3)根据本文提供的最大APF求解方法,对一款常用变频空调器的运行工况进行了优化,得到的APF比原有值提升了6.37%。3 APF约束方程组的推导
3.1 约束方程的类别
3.2 能力的约束方程推导
3.3 能效的约束方程推导

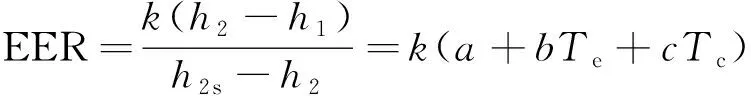
4 多约束寻优求解APF最大值
5 案例分析

6 结论

