一种基于分支条件混淆的代码加密技术
耿 普 祝跃飞
(战略支援部队信息工程大学 郑州 450002)
代码加密[1-7]和代码混淆都是重要的代码保护技术,传统的代码加密技术在加密代码的粒度上越来越细,从文件、程序节区粒度到函数[7-8]、基本块粒度,甚至到单个机器指令[5]的粒度;另外在解密函数上也引入了多态[4]的方法,加密代码每次解密执行后的再次加密会通过秘钥变化和解密函数变化来增加逆向分析的难度;但是在隐藏解密秘钥方面还缺少相关研究.分支条件混淆[9-13]是代码混淆[14]研究的一个新方向,通过混淆分支条件,能够隐藏程序执行逻辑、对抗符号执行[11,15-16],特别是在对触发条件的保护上具有较好的效果,能够阻碍生成满足触发条件的程序输入.
虽然分支条件混淆能够保护程序的触发条件,但是无法保护基于触发条件的程序代码.于是Sharif等人[9]结合分支条件混淆和代码加密,提出了一种基于分支条件混淆的条件代码加密技术,使用满足分支条件的输入作为代码加解密秘钥对条件代码进行加密,因此在程序内存中不需要存储秘钥,而是在运行时直接获取分支条件的输入作为秘钥;另外由于混淆使得逆向分析者难以获取满足分支条件的输入,也就无法获取加解密秘钥,因此结合分支条件混淆的代码加密实现了解密秘钥的隐藏.然而该分支混淆方法均只能应用于等于条件;另外,受限于解密秘钥唯一性要求,基于分支条件混淆的代码加密技术只能应用于单个等于条件的分支;这些限制极大阻碍了基于分支条件混淆的代码加密技术的应用.
王志等人[11]在Sharif[9]分支条件混淆方法的基础上,提出了一种基于保留前缀加密的分支混淆技术,把分支条件混淆从等于判断的条件扩展到大小判断的条件.然而在非等条件下,分支条件为真的输入不具备唯一性要求,因此不能使用分支输入作为秘钥对条件代码进行加密.在分支条件取值为真的输入不唯一的条件下,为解决使用分支输入产生唯一性秘钥的要求,在多输入分支条件下,结合分支条件混淆,本文提出了一种基于拉格朗日插值法的秘钥生成技术,实现了解密秘钥和分支条件混淆的结合,隐藏了代码解密秘钥.
本文的主要贡献有4个方面:
1) 基于拉格朗日插值法,在分支条件取值为真的输入不唯一的条件下,提出了一种使用分支条件输入生成代码加解密秘钥的方法;
2) 通过对多个等于条件取或形成的复合条件的分支输入进行处理,完成了多输入条件下的秘钥生成,实现条件代码加密,避免了代码复制和复合条件拆分带来的空间损耗;
3) 完成了基于分支混淆的条件代码加密方法从等于条件分支到区间条件分支的扩展;
4) 针对等于条件和区间条件通过逻辑运行形成的复杂条件,实现了分支混淆和复杂条件代码加密的结合,实现了复杂条件分支下的基于分支混淆的代码加密.
1 基础知识
1.1 前缀算法
前缀算法是一种把一个整数区间转变为一个前缀集合的算法,并且保证区间中的每一个整数均在前缀集合能找到一个与之匹配的前缀,反之在集合中没有匹配到前缀的整数一定不属于该区间.并且前缀算法得到的前缀集合元素个数有2个特点,其中n表示整数的二进制位数:
1) 区间前缀集合元素个数最大值为2n-2;
2) 区间前缀集合元素个数平均值为((n-2)×22n-1+(n+1)2n+1)(22n-1+2n-1),在32 b或者64 b程序中,该值都接近为n-2.
前缀算法伪代码如算法1所示:
算法1.一个整数区间到前缀集合的转换算法.
输入:区间起始值的二进制表示a1a2…an;区间结束值的二进制表示b1b2…bn;
输出:区间的前缀集合Prefix.
PrefixSearch_Prefix(a1a2…an,b1b2…bn)
{
for (intk=1;(k≤n) && (ak=bk);
k++)
if (k=n+1)
return {a1a2…an};
endif
endfor
if((akak+1…an=00…0) && (bkbk+1…bn=11…1))
if (k=1)
return {*};
else
return{a1a2…ak-1};
endif
endif
PrefixA=Search_Prefix(ak+1ak+2…an,11…1);
PrefixB=Search_Prefix(00…0,bk+1bk+2…bn)
return{a1a2…ak-10+PrefixA,a1a2…ak-11+PrefixB};
}
1.2 保留前缀Hash加密
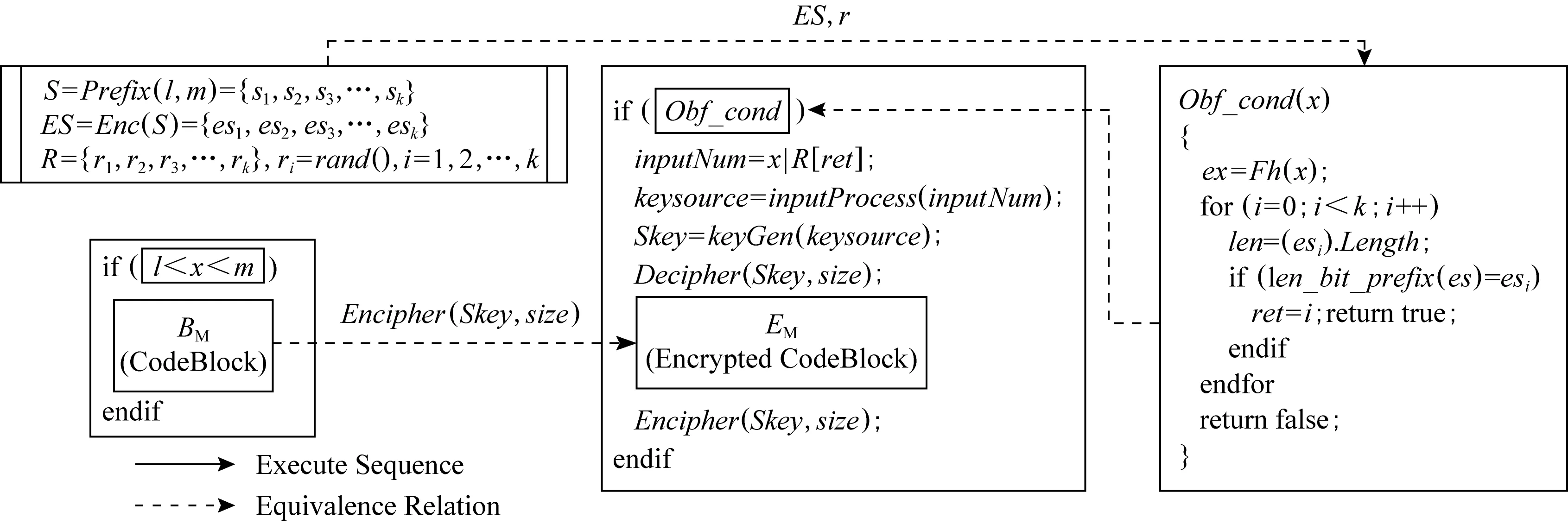
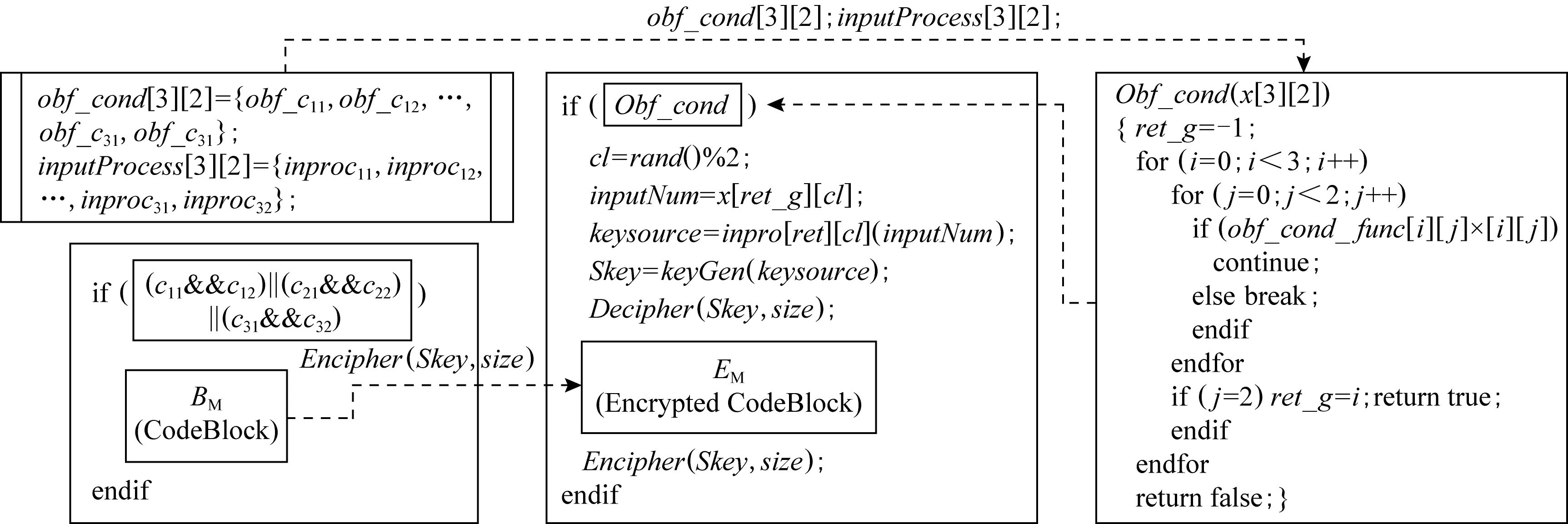
保留前缀加密[17].假设a=a1a2…an,b=b1b2…bn为2个n位整数,如果a1a2…ak=b1b2…bk,其中k 标准形式定理(canonical form theorem)[17].假设fi是一个从{0,1}i到{0,1}上的函数,其中i=1,2,…,n-1,并且f0是一个常量函数,F是一个{0,1}n上的函数,其定义对任意给定的整数a=a1a2…an,令: (1) 其中,⊕表示异或运算,i=1,2,…,n,f0为常数,可以得出结论:1)F是一个保留前缀加密函数;2)任意保留前缀加密函数必定有F的表示形式.定理的证明参见文献[6],此处省略. 保留前缀Hash加密[11]是一种把Hash函数引入到保留前缀加密计算的加密算法,表示为Fh(a)其中fi-1(a1a2…ai-1)=T(Hash(a1a2…ai-1)),其中T为取位函数,即选择Hash结果的某一位. Sharif提出的基于分支条件混淆的条件代码加密如图1所示,主要是通过分支输入生成条件代码的加解密秘钥,从而保证程序中不需要存储秘钥,实现了解密秘钥隐藏和分支条件混淆的结合.逆向攻击者解密代码的难度等同于找到使得分支条件取值为真的输入的难度,而分支条件混淆的目的正是阻碍攻击者获取使得分支条件取值为真的输入. Fig. 1 Example of conditional code encryption图1 条件代码加密示意图 Fig. 2 The process of duplicate condition and compound condition图2 重复条件代码和复合条件代码的复制处理 Fig. 3 The example of branch obfuscation based on prefix-preserving algorithm图3 基于保留前缀Hash加密的分支条件混淆示意图 另外,本文把形如a≤x≤b的条件称为区间条件,把单个的等于比较条件、单个的区间条件成为基本条件.多个基本条件通过逻辑运算组合成的条件成为复合条件. 在Sharif提出的基于分支条件混淆的代码加密方法中,对重复条件和多个等于条件取或的复合条件,需要使用条件代码复制的方法,把复合条件拆分为多个简单条件,然后再对各个简单条件的代码进行加解密,增加了混淆的损耗,同时降低了混淆的隐蔽性.如图3所示: Sharif等人[9]提出的分支条件混淆仅针对等于条件,通过使用Hash值比较代替明文比较,使得攻击者难以从Hash值比较中恢复出明文比较关系,达到分支条件混淆的目的.如对分支条件if(x=a),其中x是任意类型的值,实质就是一片内存的内容,通过分支条件混淆后变为if(Hash(x)=Hash(a)). 王志等人[11]提出了基于保留前缀加密和Hash函数的路径分支混淆技术,使用加密前缀匹配替代分支条件,实现分支条件混淆.例如分支条件if(9≤x≤15),首先把条件转换为整数区间[9,15];然后使用前缀算法获取区间的前缀集合S={1001,101*,11*};接下来使用保留前缀Hash加密算法对S进行加密得到ES;最后使用加密前缀匹配函数替换分支条件,即if(9≤x≤15)变为if(isMatch(x,ES)),其中isMatch(x,ES)如算法2所示. 算法2.isMatch算法. 输入:整数x、加密前缀集合ES; 输出:true或者false,true表示x满足分支条件,false表示x不满足分支条件. boolisMatch(x,HS) {intencPrefixofInput=encInput(x); inttmpFlag[32]={0};tmpFlag[0]=1≪31; for(inti=1;i<32;i++){tmpFlag[i]=tmpFlag[i-1]|(1≪(31-i));} for(intj=0;j {tmpLen=ES[j].prefixLen; tmpPrefix=encPrefixofinput&tmpFlag[tmpLen]; if(tmpPrefix=ES[j].prefix){return true;} } return fasle; } 基于分支条件混淆的条件代码加密,由于使用分支条件的输入作为加解密秘钥,导致该加密方法仅能用于单个等于条件的分支.对于具有多个输入值使得分支条件取值为真的分支,由于输入不具有唯一性,导致秘钥不能直接使用分支输入.因此需要对输入进行处理,使得多个输入x1,x2,x3,…输入经过处理后得到相同的输出y,使用y作为解密秘钥,从而保证秘钥的唯一性. 拉格朗日插值法是18世纪法国数学家约瑟夫·拉格朗日发明的一种多项式插值方法.用于寻找二维平面上经过n+1个点的n次多项式,使得多项式在给定的n+1个观测点能取到给定的值.经过n+1个点的次数不超过n的多项式只有一个,即拉格朗日多项式.本文使用拉格朗日插值保证多输入条件下的输出唯一性. 对给定的n+1个点(x0,y0),(x1,y1),(x2,y2),…,(xn,yn),首先根据每个点得出n+1个拉格朗日基本多项式,其中第i个点(xi,yi) 的拉格朗日基本多项式为 一方面,拉格朗日多项式的系数不是整数,即存在除法,因此在使用计算机计算的过程中可能会出现实际值与计算值有出入的问题;另外一方面,拉格朗日多项式具备鲜明的特征,给攻击者从拉格朗日多项式中获取分支输入提供了便利;最后,如果多项式的次数过低,则在某个分支输入已知的情况下会导致其他分支输入泄露,从而会导致分支条件混淆被还原.因此需要对拉格朗日多项式进行变换,以实现多项式系数的整数化、消除拉格朗日多项式的特征和提高多项式次数. 首先,通过对插值多项式L(x)进行去分母和模运算变化,使得多项式的系数整数化,同时消除拉格朗日多项式的特征.即取 使用拉格朗日多项式进行多输入分支的条件代码加密密钥生成,解决了大小比较分支的输入不唯一问题,使得条件代码加密和分支混淆紧密结合在一起,对条件代码进行更好的混淆保护.同时通过密钥构造解决Sharif条件代码加密方法中的代码复制问题,提升混淆的效率和隐蔽性. 重复条件和复合条件需要使用代码复制变转换为多个简单条件,根本原因在于能够执行到条件代码的分支输入不唯一,因此不能直接使用分支输入作为秘钥.通过对输入进行处理,使得多个输入生成相同的输出,则不需要使用代码复制的手段,减少了加密导致的空间占用.在Sharif分支条件混淆的基础上,对多输入进行处理的步骤如图4所示. 1) 判断等于条件的输入x,y是否为整数,若不是整数,则对输入进行加盐的Hash计算,然后取Hash值的前4个字节作为拉格朗日插值法的插值点的横坐标;若x,y为整数,则直接取x,y作为插值点横坐标;然后取一个随机整数作为多项式在插值点x和y处的取值,生成拉格朗日多项式. 2) 使用拉格朗日多项式变换,得到输入预处理函数inputProcess. 3) 在使用Hash值比较替代整数比较的过程中,依次判断输入x,y是否使得分支条件取值为真,使用第一个使分支条件取值为真的输入作为inputProcess函数的参数计算该分支的输出值keysource,使用keysource生成解密秘钥,最后进行条件代码的解密和再次加密. Fig. 4 The process of compound condition and duplicate condition图4 复合条件和重复条件处理示意图 对分支条件if(a≤x≤b),应用基于保留前缀加密Hash算法的分支条件混淆技术混淆后,分支条件为if(isMatch(x,ES)),其中ES={es1,es2,…,esm}为区间[a,b]对应前缀集合应用保留前缀Hash加密算法Fh计算后得到加密前缀数据.对区间条件在基于保留前缀Hash加密的分支混淆后,条件代码加密过程如图5所示,加密步骤如下: Fig. 5 Example of interval condition process图5 区间条件分支处理示意图 1) 对n位整数区间[a,b],计算其前缀集合S={s1,s2,…,sk},对j位前缀元素si,取随机数ri的尾部n-j比特与si一起组合成n位整数ti,使用t1,t2,…,tk作为拉格朗日插值点的横坐标,取随机数tmp作为所有插值点的纵坐标,计算输入预处理函数inputProcess.保存随机数数组R={r1,r2,…,rk}. 2) 在算法2中,若x使得isMatch返回true,则在isMatch中记录与x相匹配的加密前缀esi的下标i,获取esi对应前缀的位长,假设为m;然后取x的前m位和ri的后n-m位组合成inputProcess函数的输入inputNum,计算得到分支的输出keysource,然后使用keysource生成解密秘钥key,使用key进行条件代码的解密和再次加密. 由等于条件和区间条件通过逻辑运算形成的复杂条件中,复杂条件的混淆是通过对构成复杂条件的每个基本条件进行混淆而完成;秘钥生成则是通过对每个基本条件进行单独的输入处理,但是需要保证每个基本条件在其输入使得条件取值为真时的输出都是相等的.为统一表示,令等于条件if(x=a)混淆后为if(isMatch(x,ES)),但是在等于条件下,isMatch算法变为{returnmemcmp(Hash(x),ES,hashLen);},其中ES为a的Hash值;令等于条件if(x=a)的输入处理函数为inputProcess(x),等于条件下的inputProcess函数伪代码如下: inputProcess(x) { if (xis interger){returnx;} else {inttmp=Hash(x); returnfirstFourBytes(tmp);} } 下面介绍复杂分支条件下的代码加密过程,加密示意图如图6所示. 1) 根据与运算和或运算的结合律:(c11)&&(c12‖c13)=(c11&&c12)‖(c11&&c13),把复杂条件转换为基本条件与运算结合成的复合条件的或运算式,即形如(c11&&c12)‖(c21&&c22)‖(c31&&c32),其中cij表示基本条件;记无或运算相隔的与运算条件为一组,即group[0]={c11,c12},group[1]={c21,c22},group[2]={c31,c32}共3组. 2) 对分支条件if((c11&&c12)‖(c21&&c22)‖(c31&&c32))的每个基本条件进行混淆,混淆后的分支条件为if(isMatch(x11,ES11) &&isMatch(x12,ES12))‖(isMatch(x21,ES21) &&isMatch(x22,ES22))‖(isMatch(x31,ES31) &&isMatch(x32,ES32))). 3) 对每个基本条件cij分别计算输入其输入处理函数,并记为inputPrecess[i][j];设函数inputPrecess[i][j]的分支输出为为Yij,randA为一随机整数数,并令Rij=randA-Yij,修改inputPrecess[i][j]=inputPrecess[i][j]+Rij,则修改后所有基本条件的预处理函数inputProcess[i][j],在其输入为使得条件Cij取值为真的分支输入值时,预处理函数的取值均为randA. 4) 在混淆后复杂条件执行时,按照顺序计算每组条件与运算的取值,找到第1组取值为true的条件.假设第i组条件与运算的取值为true,则随机选择第i组条件中的任意一个条件代表该复杂分支条件进行分支输出计算,假设选中条件为Cij,则选取inputProcess[i][j]为复杂分支条件的输出计算函数,选取x[i][j]为inputProcess[i][j]的计算参数,计算结果则为randA,使用randA计算秘钥,然后对条件代码进行解密和2次加密. Fig. 6 Example of complicated condition process图6 复杂条件分支处理示意图 Fig. 7 The encipher and decipher example of multi-thread code图7 多线程代码加解密示意图 如果需要加密的代码是一段多个线程共用的代码,则在解密和2次加密的过程中需要进行加解密的操作同步,否则会导致加解密错乱,程序执行出现不可控错误.本文采用临界区对加加解密操作进行同步,解密操作在进入临界区后首先判断加密代码是否在使用中.如果否,则解密;如果是,则不需要解密、直接返回,退出临界区. 同样,在2次加密的过程中,进入临界区后首先判断需要加密的代码是否在使用中.如果否,则对代码进行2次加密;如果是,则加密函数直接返回,退出临界区.处理过程如图7所示. 由于本文提出的代码加密是基于分支条件混淆,因此时间和空间的消耗都是基于分支条件已经被混淆的程序来计算的. 首先是加密算法消耗的存储空间,本文采用AES-128加密算法对条件代码进行加密,AES算法源代码通过编译得到的obj文件占用空间为58 807 B;其次inputProcess函数通过把系数和最高次数记为参数后,该函数的算法占用416 B.上述算法是所有的分支条件代码加密所共用的代码,因此随着被选择加密的分支条件越多,每个分支占用的共用空间就越少.另外由于每个分支条件需要存储自己的多项式系数,需要增加加密和解密的外包函数,因此每个分支条件单独占用的空间平均是30×4+83+83=283 B.即对单个区间条件构成的分支,对m个分支条件的代码进行加密,平均每个分支条件的代码加密需要消耗283+(416+58 807)m字节的空间.如果是m个复杂条件,且每个复杂条件由k个基本条件构成,则每个复杂分支平均消耗120×k+(416+58 807)m字节的空间用于代码加密. 其次是时间消耗,时间消耗主要在于AES128一次加密和解密的时间,即平均每个分支多消耗0.003 3 ms(由10 000次AES加密和解密消耗32.8 ms时间计算得到单次加解密时间). Table 1 Consumption Data of Time and Space表1 加密消耗的时间和空间数据 Sharif第1次提出了基于分支条件混淆的代码解密方法,通过分支条件混淆实现了秘钥隐藏;通过逆向分析获取加解密秘钥的的难度,等同于找到使得被混淆分支条件取值为真的程序输入的难度.即相比其他的加密方法,基于分支条件混淆的代码加密方法能更好的对抗解密秘钥获取攻击. 在基于分支条件混淆的代码加密研究方面,除了Sharif在基于等于条件混淆的代码加密研究外,还没有相关的研究.与Sharif的加密方法相比,本文提出的方法在2个方面具有优势: 1) 把Sharif的方法从等于条件扩展到了区间条件和复杂条件,具有更好的通用性; 2) 对多个等于条件取或的分支,本文提出的方法不需要代码复制,从而节省了代码占用的空间. 综上所述,本文提出的代码加密方法在时间和空间消耗上是可接受的;由于解密秘钥通过分支混淆隐藏,使得加密后代码能较好对抗逆向分析,因此该加密方法能够实际使用,且具有比较好的代码保护功能. Table 2 Comparison of Different Methods表2 加密方法优势对比 基于分支条件混淆的条件代码加密,通过满足分支条件的输入产生秘钥,同时利用分支混淆隐藏分支条件,从而隔离秘钥和程序,极大地提高了解密难度.由于秘钥生成和分支条件紧密联系在一起,只有在加密的条件代码所在分支因正确的输入而得到执行时,通过分支输入可以计算出秘钥,实现解密,否则就会导致解密错误,产生不可预测的错误导致程序运行终止.虽然基于分支条件混淆的条件代码解密具有较好的抗程序分析效果,但是当前研究仅能在等于条件分支上实现该类加密方式,极大地限制了该方法的使用.本文通过构建输入预处理函数,对具有多个正确输入的分支进行处理,完成了多输入分支下利用分支输入产生具有唯一性秘钥的方法.利用该方法,对多个等于条件取或的分支和重复条件代码分支的条件代码加密进行了优化,减少了加密对空间的消耗;区间条件分支使用基于保留前缀加密和Hash函数的分支混淆方法进行分支条件混淆,本文使用整数区间对应的前缀集合生成输入预处理函数,实现了区间条件分支下基于分支输入产生唯一性秘钥的方法,从而对区间条件分支的条件代码进行加密.最后对等于和区间条件复合而成的复杂条件分支进行处理,对该分支同样实现了基于分支输入产生唯一性秘钥的方法,进而对条件代码进行加密.通过以上处理完成了基于分支条件混淆的条件代码加密从等于条件分支到区间条件分支和复杂条件分支的扩展,提高了代码保护的范围,增强了代码安全性.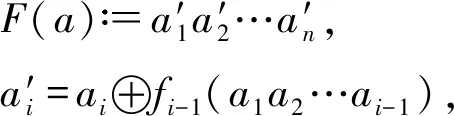
1.3 Sharif提出的条件代码加密方法介绍
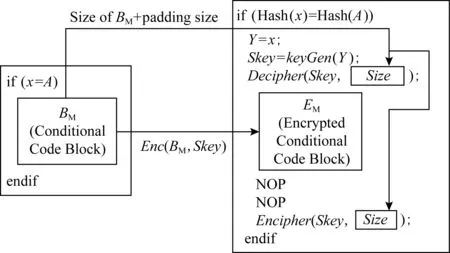
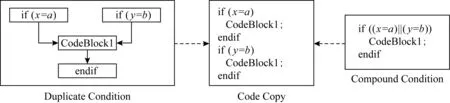

1.4 基于保留前缀加密的分支混淆方法介绍
2 多输入条件下的秘钥生成
2.1 拉格朗日插值法
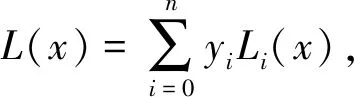
2.2 输入处理多项式生成
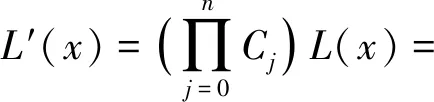
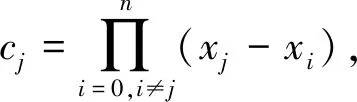
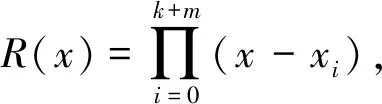
3 基于分支条件混淆的条件代码加密
3.1 Sharif条件代码加密方法的改进
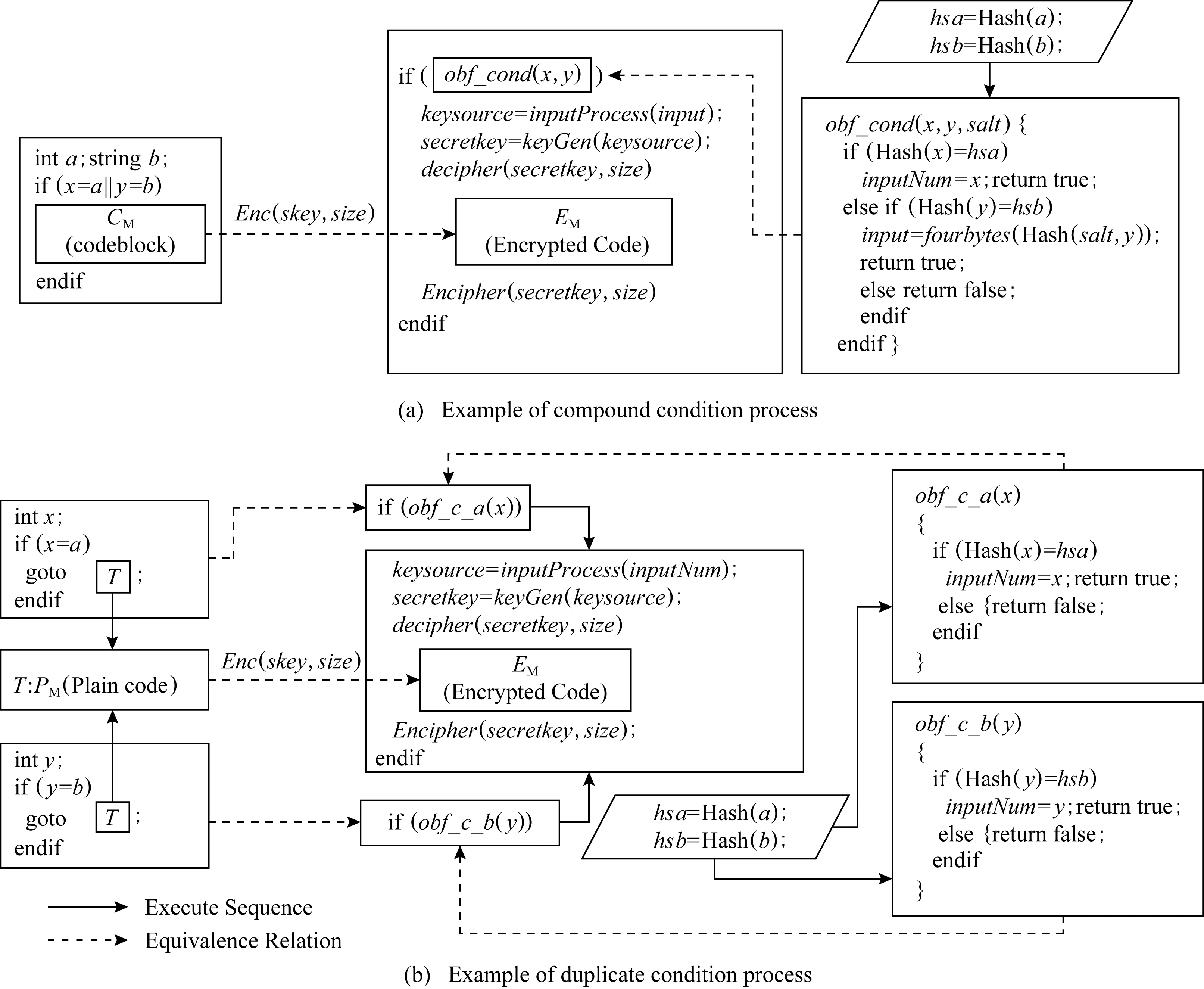
3.2 大小比较分支的条件代码加密
3.3 复杂条件分支的条件代码加密

3.4 多线程处理
4 分析与评估
4.1 条件代码加密的时间和空间消耗

4.2 与其他加密方法的比较

5 结 论

