支持属性撤销的可追踪外包属性加密方案

高嘉昕 孙加萌 秦 静

(山东大学数学学院 济南 250100)

随着社会发展，数据呈现爆炸性增长，用户对计算机的存储和计算能力有了更高要求，由于资源和成本的限制，用户往往拥有有限的计算和存储能力，难以达到数据处理所需要的条件.在这种背景下，云服务器的概念就产生了.服务商平台陆续为用户提供云服务器来解决用户的资源受限问题，如华为云、阿里云、百度云等.信息上传到云服务器存储和加密，为用户带来便利的同时也出现了安全问题，即云服务器并不是完全可信的.用户的敏感信息上传到云服务器后，一方面信息脱离了用户的物理掌控，用户不能确保信息的隐私性和正确性；另一方面用户的敏感信息未经处理上传到云服务器，云服务器的管理者可以访问数据并窃取敏感信息，数据的隐私性遭到破坏.2011～2014年间约有11.4亿人遭遇隐私数据被泄露的危机.2012年苹果ICloud的访问控制出现问题，导致大量用户存储在ICloud的数据被盗，不仅给用户造成了巨大的损失，也给苹果公司的股价和形象带来了负面影响[1-2].随着技术的发展，访问控制在云计算中拥有越来越高的地位.而在云计算中，目前应用较为广泛的访问控制是基于属性加密技术.

基于属性的加密(attribute-based encryption, ABE)[3]是一种新型加密原语，在云计算中有着广泛的应用.在ABE体制中用户的私钥和密文分别用一组描述属性和访问策略标记，当描述的属性与访问策略相关联时，即私钥与密文相关联时才能正确解密.ABE有2种形式：密钥策略ABE(key-policy ABE,KP-ABE)和密文策略ABE(ciphertext-policy ABE,CP-ABE).KP-ABE是指密文由属性标记，私钥由访问策略标记.而在CP-ABE中私钥由属性标记，密文由访问策略标记，由数据发送方决定访问策略.ABE体制中用户可以设置访问策略，并决定与访问策略相关联的属性，即哪些属性可以解开密文，因此用户对数据具有灵活的访问控制权.基于属性的加密技术可以在云服务器不完全可信的情况下，通过访问控制保障云服务器中的数据安全.但是属性加密中密钥分配和解密计算的巨大开销和存储量，使得计算能力不足的用户很难应用属性加密技术保障信息安全.

为了解决这个问题，Green等人[4]和Zhou等人[5]提出在不泄露隐私数据和密钥的前提下将ABE体制中的解密阶段外包给云服务器计算.即将属性加密中计算成本大的部分外包给云服务器计算，解决了用户计算负担过重的问题，也加快了方案的运行效率.文中所构造的方案在不受信任的云服务器环境下，虽然减少了用户的计算和存储开销，但是用户无法对服务器返回的结果进行验证.2014年Li等人[6]提出了引用计算委托(refered delegation of computation, RDoC)的模型，首先方案支持密钥委托生成，将部分密钥生成过程外包给k个服务器，在权限端进行验证并生成转化密钥，既加快了方案运行效率，又完善了部分外包计算的可验证性，解决了用户不能对返回结果验证的问题，这是第1次考虑部分外包ABE的可验证性；其次将部分解密工作外包给服务器计算，减少了用户的计算负担，通过盲化密钥保护解密密钥的安全性.但是该方案中数据消息未经处理直接发送给云服务器，不能有效保护数据的隐私性，同时也不支持属性撤销和可追踪性.

本文基于Li等人[6]的ABE方案构造了一个可验证的外包KP-ABE方案，本文方案使用具有高表达性的树形访问策略，提供了更细粒度的访问控制，丰富了属性之间的逻辑关系；将加密阶段分为线上、线下2部分进行，线下加密指将部分只需要公钥进行的计算转移至线下进行，既减少用户计算存储量，又有效保护用户数据的隐私性；面对不可避免的用户访问权限变更问题，本文通过重加密的方法生成重加密密钥更新属性与密文，间接撤销单个属性，达到细粒度属性撤销，实现用户的动态加入及退出；最后将用户身份嵌入到用户私钥中，通过泄露的密钥即可追踪到用户身份，有效解决了密钥的泄露问题，防止合谋攻击.

1 相关工作

1.1 基于属性的加密

ABE体制最初由Sahai和Waters[3]于2005年提出，正式提出了满足可容忍误差性和防止串谋攻击性的生物识别技术与基于属性加密技术.文中首次将身份与一组属性相关联，并正式给出了基于多项式插值的ABE具体构造方案.随后2006年Goyal等人[7]提出了由数据接收方规定访问策略的KP-ABE，解决了基于属性加密技术无法支持灵活的访问控制问题.2007年Bethencourt等人[8]首次详细描述了CP-ABE方案以及CP-ABE的特性，文中所构造的CP-ABE方案的访问控制由更为灵活的树形访问结构描述，在典型的访问控制树中，非叶子节点为陷门，叶子节点为属性值.树形访问结构也是ABE方案中应用较为广泛的访问控制.

在实际应用中，ABE系统也难免面临着用户权限的改变、用户的删除与更新等问题，在2010年Yu等人[9]提出了CP-ABE的属性撤销方案.在这篇文章中采用了半可信的代理服务器进行代理重加密技术，在撤销属性时只需生成重加密密钥即可，并在文中提出了KP-ABE的大属性空间撤销方案.但是ABE中关于访问结构中关联的一系列属性以及其他运算的高额运算量依旧没有得到解决，Hohenberger和Waters在2014年提出了线上线下ABE[10]，通过将部分计算转移到线下减少线上的计算量，有效地提高计算效率，减少用户的计算量.

随着互联网的快速发展，移动终端与云存储的结合成为未来趋势，但是移动终端的计算资源受限，传统的属性加密技术往往需要大量的计算，给属性授权机构和移动终端带来严重的计算负担，相关学者提出将外包计算与属性加密技术相结合达到减少用户计算负担的目的.2017年，Zhao等人[11]提出了面向移动云计算的外包ABE方案.该方案支持加密外包和解密外包，解决了基于属性加密的高效性带来的解密计算中的高额计算量.Fan等人[12]提出了一种多授权中心的可验外包计算.Zhang等人[13]提出一种完全外包ABE方案，即将密钥生成、加密和解密都外包给云服务商，并且完成了方案的安全性证明.但该方案无法完成外包计算正确性的验证，而可验证性对于正确计算至关重要.Li等人[14]提出一种新的可验证外包解密计算，该方案只实现了解密外包，而数据拥有者仍然需要大量计算完成数据加密任务.2014年Li等人[6]提出了一个同时支持密钥生成和解密外包的属性加密方案，将密钥生成和部分解密工作外包给不同的服务器计算，使得资源受限的用户也可以进行计算繁重的任务.该方案不仅减轻了用户的计算负担，也对返回结果的正确性进行验证，但是方案中用户上传到云服务器的数据隐私性等问题仍没有解决.

2019年Zhao等人[15]提出一种可验证的完全外包的CP-ABE方案，即将密钥产生、加密和解密都外包给云服务商，并完善了完全外包方案的可验证性，并且给出了该方案的选择明文攻击下的不可区分性安全和可验证安全性证明.

1.2 外包计算

外包计算是一项新兴技术，它有效地解决了计算能力及存储空间不足等问题.Chaum等人[16]在1995年提出了外包密码运算的雏形，即通过在用户的设备上安装安全的硬件来帮助用户完成复杂的计算.随后在2005年Hohenberger等人[17]给出外包计算的安全定义,并且提出了一个全新的外包计算方案，文中具体算法是基于模指数运算提出的.2010年Gennaro等人[18]首次提出了非交互式可验证计算的概念，并且基于混淆电路和全同态加密提出一个适用于任意运算的可验证的外包计算，将待计算的函数转化成相对的电路函数.2011年Green等人[4]给出了支持解密运算外包的基于属性加密方案，但是方案没有考虑到用户对于返回结果的验证问题.随后Lai等人[19]通过增加密文冗余的方法改善了之前不支持外包计算结果的正确性验证.

Dong等人[20]提出了基于双线性对的完全可验证安全外包.2014年Li等人[6]提出了一个同时支持密钥生成和解密外包的属性加密方案，既能达到将计算外包的目的，也可以对返回结果的正确性进行验证.随后出现了大量以数学运算为基础的安全外包，2015年Chen等人[21]利用稀疏矩阵提出一个安全的矩阵外包方案.2016年Yu等人[22]对大规模线性方程组求解的安全外包进行了深入研究，2017年Kumar等人[23]提出了对于恶意的云服务器如何利用矩阵乘法安全外包.

1.3 线上线下技术

最初在1989年Even等人[24]提出了线上线下签名的概念，作者在线下进行签名的高计算率部分，将轻量级的计算在线上进行，虽然有效减少了计算量，但是增加了签名的长度.随后，2001年Shamir等人[25]提出了一个更高效的线上线下签名方案，所提出的线上线下签名无需将签名的长度增加一个二次因子.

2008年Guo等人[26]正式提出基于身份的线上线下加密方案，在这个方案中将加密过程分成线上加密和线下加密2个部分，线下完成大部分加密计算，但不知道消息与接收方的身份，保存部分密文，线上只需要进行少量的加密计算即可得到密文.线上线下加密既有效保护信息安全性，又减少存储空间和计算成本的浪费.

2 预备知识

2.1 符 号

本文所用到的缩略词如表1所示:

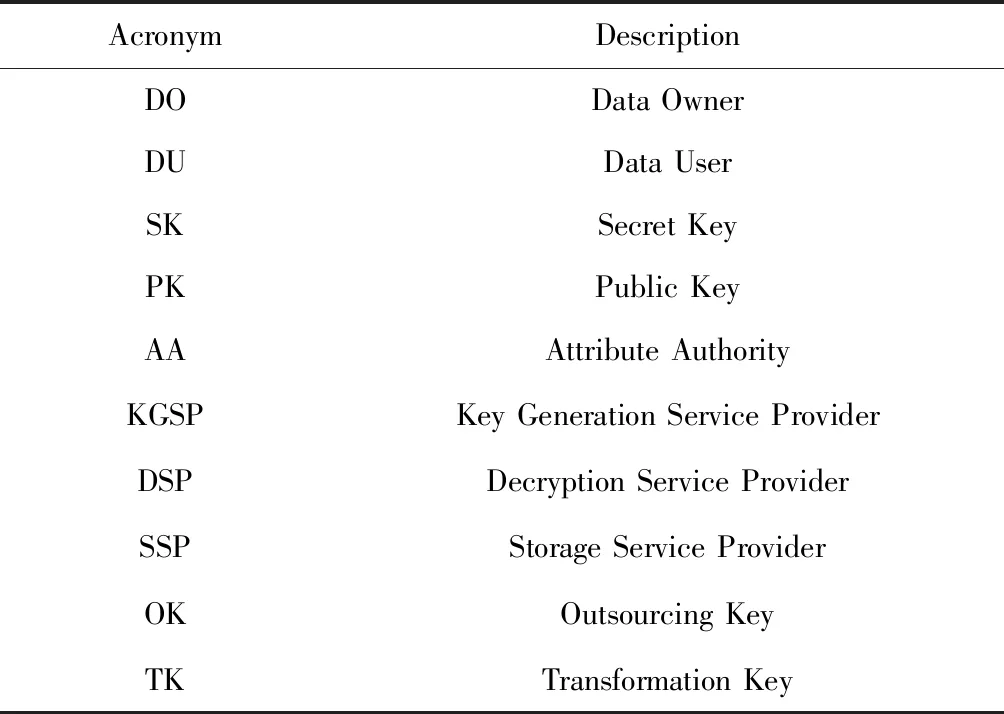
Table 1 Related Terms and Their Acronyms

其中，本文中属性机构AA是可信任的，但密钥生成服务商KGSP、云存储服务商SSP和解密服务商DSP是“诚实且好奇”(honest but curious)的，即云服务器会遵守协议，但是会试图获取更多的隐私信息.

2.2 相关定义

定义1.访问结构.设{P1,P2,…,Pn}为n个参与者的集合，如果∀B,C满足B∈A,B⊆C,则C∈A,集合A⊆2{P1,P2,…,Pn}是单调的.其中属于A的集合称为认证集.此外本文定义γ(·，·)，

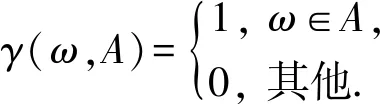
定义2.访问树.在一棵访问树中，其根节点为r，所有的叶子节点m均为输入的属性值，每一个节点关联一个dm阶多项式qm(·)，其中dm=km-1，km为该节点的门限值.所有的非叶子结点m则是门限值为km的陷门，其中非叶子节点m拥有numm个孩子节点.在访问树中，定义操作：

parent(m)表示节点m的父节点，children(m)表示节点m的子节点，index(m)表示兄弟节点中的序号，att(m)表示叶子节点所关联的属性.

定义3.双线性映射.设置2个阶为素数q的乘法循环群G和GT，g是G的一个生成元.存在一个双线性映射e:G×G|→GT，满足3个属性：

2) 非退化性.∃g1,g2∈G满足e(g1,g2)≠1.

3) 可计算性.∀g1,g2∈G，计算e(g1,g2)是有效函数.

2.3 困难假设

定义4.判定双线性Diffie-Hellman问题(decision bilinear Diffie -Hellman problem, DBDH).假设给定一个四元组(g,ga,gb,gc)，其中g是阶为q的乘法循环群G的生成元，a,b,c,z∈Zq，区分2个四元组(ga,gb,gc,e(g,g)abc)和(ga,gb,gc,e(g,g)z).如果对于多项式时间内解决DBDH的概率是可以忽略的，就说DBDH问题是困难的.

3 模型定义

3.1 VDC-KP-ABE方案模型

图1给出本文所提VDC-KP-ABE(delegation of computation KP-ABE with verifiability)方案模型.

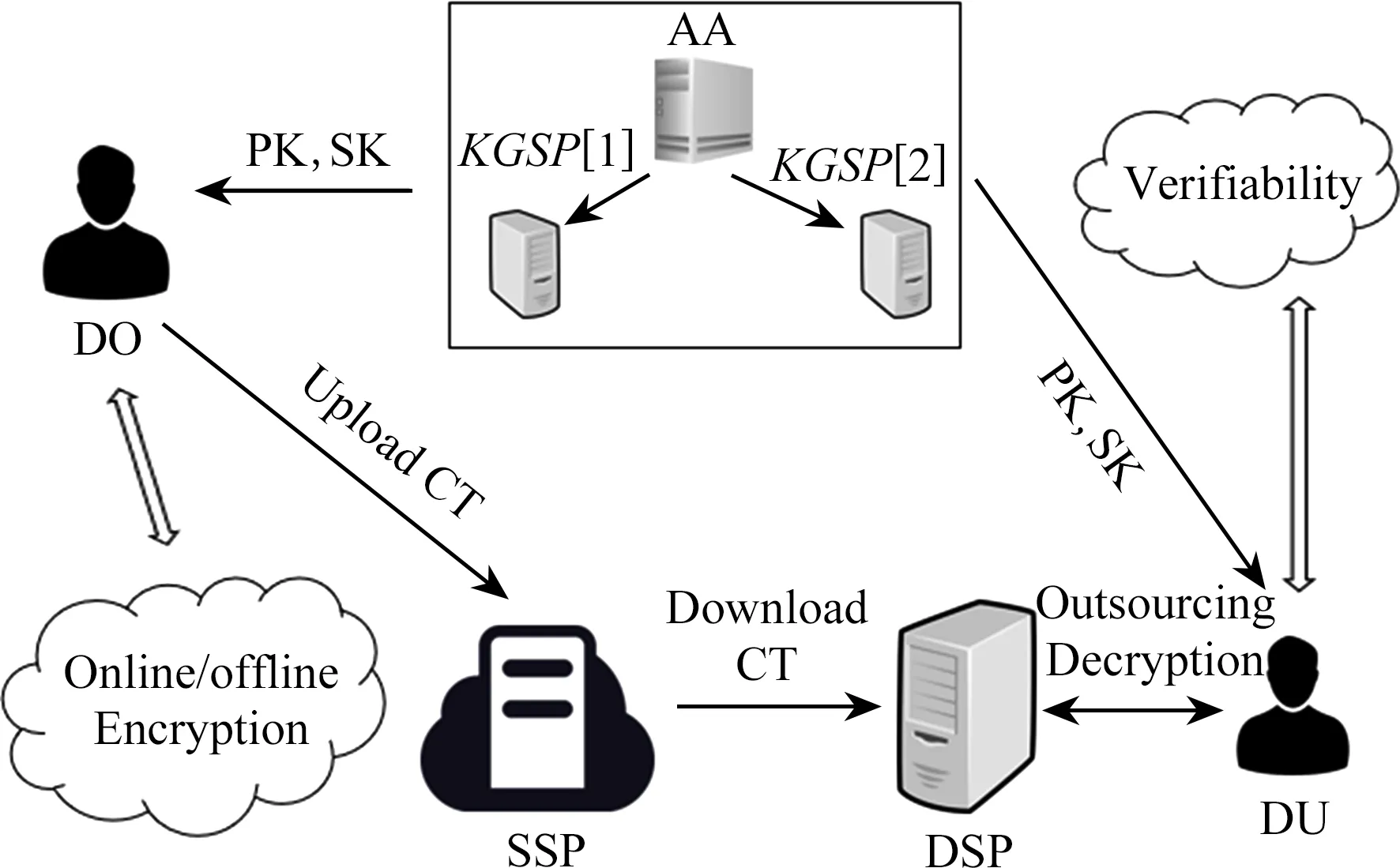
Fig.1 System model for this paper图1 本文方案的模型

用户向AA请求密钥，AA将密钥生成阶段外包给KGSP[i]进行，对返回结果进行检验后将密钥发送给用户.用户将密文发送到SSP存储，解密过程中，用户从SSP中搜索下载密文，并将解密工作外包给DSP进行，用户可以对返回结果进行验证.

在密钥分配过程中，为了防止KGSP与DSP串通下的不诚实行为，利用AA生成的d-1阶随机多项式gRG(·)，将gRG(·)与另一个多项式以随机的顺序发送给KGSP[i].KGSP利用多项式生成部分转化密钥，AA只需要检验由gRG(·)计算的部分转化密钥即可.

记A为访问策略，ω为属性集合.

根据系统模型，算法定义：

1) 初始化算法

Setup(λ)→(PK,MK)：AA运行该算法，输入为系统的安全参数λ.输出为公钥PK和主密钥MK.

2) 密钥生成

KeyGeninit(A，MK,ID)→(S[i]REAL,SRG)：AA运行密钥生成初始化算法，输入属性访问策略A和主密钥MK，输出一对外包密钥集(OKKGSP[i],OKAA)和一组基于外包密钥OKKGSP[i]生成的数对(S[i]REAL,SRG).

KeyGenout(S[i]REAL,SRG)→(TKKGSP[i],TKRGi)：KGSP[i]被委托计算部分转化密钥，即运行密钥生成算法.算法中的输入为(S[i]REAL,SRG)，最终输出部分转化密钥对(TKKGSP[i],TKRGi).

KeyGenin(A,OKAA)→TKAA：由AA运行内部密钥生成算法，输入为树形访问策略A和AA的外包密钥OKAA，输出另一个部分转化密钥TKAA.

KeyCheck(TKKGSP[i],TKRGi,ID)→TK：AA对KGSP发回的结果进行检验，通过验证后输出转化密钥TK.

KeyBlind(TK)→(SK,TK′)：由AA计算，输入转化密钥TK，输出私钥SK和盲化密钥TK′.

3) 加密算法

Encryptoff(PK)→CToff：线下执行加密算法，输入公钥PK，输出部分密文CToff.

EncryptU(M,CToff,γ)→(CT,VK)：用户进行加密计算，输入消息M、加密属性γ和部分密文CToff，输出密文CT和验证密钥VK.

4) 解密算法

Decryptin(CTpart,SK,VK)→M⊥：用户执行最后解密算法，输入部分解密密文CTpart、私钥SK和验证密钥VK，首先对DSP返回结果进行验证，若通过验证，输出明文M，否则输出⊥.

5) 属性撤销

ReKeyGen(θ,MK)→rk：由AA计算，输入更新的属性集θ，和主密钥MK生成重加密密钥rk.

ReEnc(E,rk,β)→CT′：输入属性集β、密文CT和重加密密钥rk，输出更新后的密文CT′.

ReKey(SK,rk)→SK′：输入密钥SK和重加密密钥rk，输出更新后的密钥SK′.

6) 追踪算法

单JSON 格式也存在诸多问题，保密性不高，缺少专用的加密技术框架，导致JSON 存在泄密的可能。JSON 数据和XML 数据功能结构的相似性,且有成熟的加密技术框架。因此，采用XML 的加密传输技术对JSON 数据进行出加密传输。XML 通常的加密方式是加构建在PKI 体系结构上。但PKI 体系存在认证效率低，数字证书管理复杂等问题[3]。

Trace(SK)→ID：输入密钥SK，对密钥进行验证是否为正常，如果通过验证，则可以得知密钥所属用户的ID.

3.2 安全模型

1) 选择安全性游戏

考虑未授权和授权已撤销2种攻击者，重加密密文与原始密文分布相同，因此只讨论原始密文的安全性.本文针对所提出的VDC-KP-ABE方案描述攻击者A与挑战者B之间的游戏如下：

初始化.攻击者A选择要挑战的一个属性集合和撤销的属性列表发送给挑战者B.

系统建立.挑战者B运行本文方案的Setup阶段，将公钥发送给攻击者.

询问阶段1.攻击者可以询问关于访问策略属性的私钥，其中属性不属于访问策略，或者属性属于撤销属性列表中.

挑战：挑战者对于攻击者发送的消息M0,M1，挑战者随机投掷一枚硬币v∈{0,1}，在属性集和撤销的属性列表下对Mv进行加密，并将结果返回给攻击者A.

询问阶段2.重复询问阶段1的步骤.

猜测.攻击者输出对v的猜测v′，若v′=v，则攻击者赢得游戏.

2) 可验证性游戏

可验证性可以验证外包阶段的算法是否有被正确执行.通过攻击者A与挑战者B之间的交互描述VDC-KP-ABE方案的可验证性.

初始化.攻击者A选择要挑战的2个Hash函数.

系统建立.挑战者B运行本文方案的Setup阶段，将公钥发送给攻击者，自己保留主私钥.

询问阶段1.挑战者B按照方案算法生成方式适应性回答攻击者A的询问

挑战.攻击者A提交一个密文M*和一个访问策略A*，挑战者B运行Enc算法获得密文CT*和验证密钥VK*.

询问阶段2.重复询问阶段1的步骤，但是攻击者不可以询问属于访问策略A*的属性.

猜测阶段.A输出转换密文CT*part.若Decryptin(CT*part,RK*,VK*)∉(m*,⊥),则攻击者A赢得了游戏.

定义6.可验证性安全.若无多项式时间攻击者以不可忽略的优势攻破上述安全模型，那么我们就说本文提出的方案具有可验证性.

4 本文方案

在密钥委托生成过程，本文利用一个混合密钥策略Policy=PolicyKGSP∧PolicyAA,其中∧是连接2个子策略的和门，PolicyKGSP是用于用户请求的属性集，PolicyAA是用于一个“不重要”的属性.称之为“不重要”属性的原因是每个请求的属性集都附加一个对整个访问控制策略没有影响的“不重要”属性θ.利用这个技巧可以随机生成一个外包密钥OKKGSP，无需主密钥和私钥的前提下，将密钥生成阶段外包给KGSP进行.

4.1 VDC-KP-ABE方案构造

1) 初始化算法

Setup(1λ)：定义属性全集U和身份全集I.首先，将全集U和I中的属性定义为Zq中的元素.简单起见取Zq中前n个元素为全集.定义Hash函数H:{0,1}*→Zp，H0:{0,1}*→{0,1}λ，H1:{0,1}2λ→{0,1}*.选择一个生成元g∈RG，整数x,a,w,w1,w2,…,wn∈RZq，并设g1=gx，W=gw,Wi=gwi，选择元素g2∈RG.最终输出公钥PK=(g,g1,g2,W,W1,…,Wn,H,H0,H1)和主私钥MK=(x,a,w,w1,…,wn).

2) 密钥生成

KeyGeninit：AA选择x11,x12∈RZq，并设OKAA=x2=x-x11-x12modq.接下来随机选取dm阶多项式fm(·)，pm(·).满足：

①i=att(m)时，fm(i)=pm(i)；

②fm(0)=x11；

③pm(0)=x12；

④fm(i)+pm(i)=qm(i)，其中i=att(m)，att(m)表示叶子节点所关联的属性.

选择一个随机多项式gRG(·).此外，选取rKGSP[1],i,rKGSP[2],i,rRG,i∈Zp，满足rKGSP[1],i=rKGSP[2],i，ri=rKGSP[1],i+rKGSP[2],i，i=att(m).最后，AA将(S[1]REAL,SRG),(S[2]REAL,SRG)分别发送给KGSP[1],KGSP[2].其中:

S[1]REAL=(fm(0)H(ID),{rKGSP[1],i}i=att(m))，
S[2]REAL=(pm(0)H(ID),{rKGSP[2],i}i=att(m))，
SRG=(gRG(·),{rRG,i}i=att(m)).

KeyGenout:KGSP[j]计算部分转化密钥，即TKKGSP[j]=({d[j]i0,d[j]i1}i=att(m))和TKRGj=({d[RGj]i0,d[RGj]i1})，并将(TKKGSP[j],TKRGj)发送给AA.其中:

KeyCheck：AA检查所有的KGSP都是正确的输出，也就是检验

d[1]i0=d[2]i0，d[1]i1=d[2]i1；

d[RG1]i0=d[RG2]i0，d[RG1]i1=d[RG2]i1；

其中，i=att(m).

通过计算di0=d[1]i0·d[2]i0，di1=d[1]i1×d[2]i1，i=att(x)将部分转化密钥合并,并输出转化密钥TK=({di0,di1}i∈A∪θ).

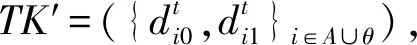
3) 加密算法

Encryptoff：选择一个随机数s∈RZq，然后计算K=e(g1,g2)s，C0=gs，Ci=(g1Wi)s，生成部分密文CToff=(K,C0,{Ci}i∈U).

EncryptU：用户在明文后附加一串冗余，即MT=M‖0k，用来在解密后检验DSP是否有不诚实行为；计算C1=MT×KH(ID)，VK=H1(H0(KH(ID))‖C1)，生成密文CTS=(γ∪θ,C1,C0,{Ci}i∈γ∪{θ})和验证标志.

4) 解密算法

Dncryptout：首先定义一个递归算法DecryNode(E,D,m)，记i=att(m).

① 若m是叶子节点，则:

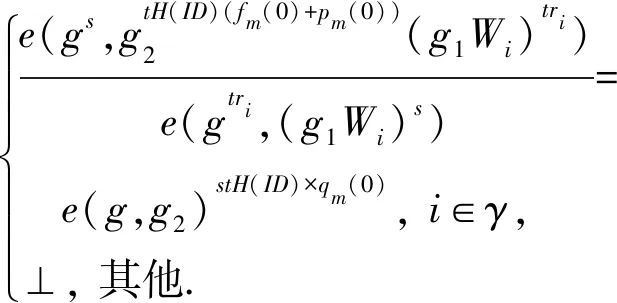
② 若m非叶子节点，那么对于m的任意孩子节点z调用递归算法DecryNode(E,D,m)，并将输出记为Fz.Sm是任意numm个子节点的集合，则:

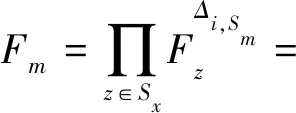
若密文满足访问策略树，则该递归算法将返回计算结果:

e(g,g2)xtsH(ID)=e(g1,g2)tsH(ID).

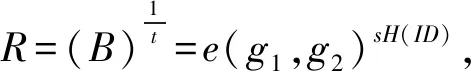
用户检查是否附有一个冗余0k.如果是，则可以得到M；否则DSP则存在不诚实的行为，输出终止符⊥.

5) 属性撤销

6) 追踪算法

验证用户身份密钥是否满足e(D0,g)=e(D1,g)e(g1,g)，当通过密钥检查时，可直接通过D2查询拥有密钥的用户身份.

4.2 分 析

4.2.1 安全性分析

4.2.1.1 选择性安全

定理1.在DBDH的假设下本文所构造的VDC-KP-ABE方案具有不可区分选择明文攻击(indistinguishable chosen-plaintext attack, IND-CPA)安全.

证明. 若攻击者可以在一个概率多项式时间内以不可忽略的优势ε在IND-CPA安全模型下攻破本文方案，那我们就能创建一个挑战者B能够以不可忽略的优势解决DBDH问题.因此在分析中我们主要的任务是提供一个挑战者和攻击者之间的真实方案的正确模拟.

假设挑战者随机翻转一个二进制硬币μ.当μ=0时，四元组为(X=gx，Y=gy，Z=gz，T=e(g,g)xyz)；否则，四元组为(X=gx，Y=gy，Z=gz，T=e(g,g)v).其中x,y,z,v∈Zq，挑战者B输出μ′作为μ的猜测值.

1) 初始化

挑战者B运行身份为ID的攻击者A，并且接受挑战属性集ω和撤销列表R.

2) 系统建立

3) 查询阶段1

grKGSP[b],i}i∈U-R),

挑战者B设置

① 当询问的属性满足访问结构，但询问的属性属于撤销列表时，

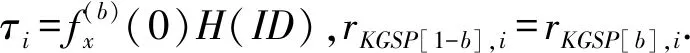
② 不满足访问结构时，

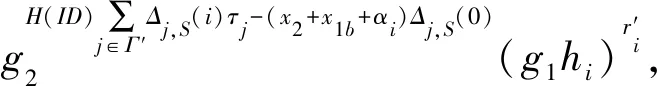
此外，di0=d[b]i0×d[1-b]i0，di1=d[b]i1×d[1-b]i1，其中i∈U，挑战者B将计算TK=({di0,di1}i∈(U-R)∪θ)，并设置j=j+1，将(j,ω,·,x1b,x1(1-b),·)加入T后，返回x1b.

挑战者B验证(i,ω,·,x1b,x1(1-b),·)是否存在T中，若存在，则返回私钥SK；否则返回终止符⊥.

4) 挑战

攻击者A向挑战者B提交2个明文M0,M1.挑战者B随机投掷硬币v，选择随机数r∈RZP,并返回明文Mv加密后的结果，密文被模拟为

CT*=(ω∪θ,rMvTH(ID),gz,g-zα,{gzαi}i∈ω∪θ).

注意：

① 如果μ=0，则T=e(g,g)xyz.如果s=z，则:

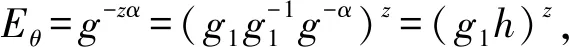
其中,i∈ω∪θ.

② 如果μ=1，则T=e(g,g)v，那么C0=rMve(g,g)v.因为v是随机的，在攻击者A的视图里C0也是随机的，因此加密后的消息不包含Mv的任何信息.

5) 查询阶段2

重复查询阶段1.

6) 猜测

攻击者A提供一个v的猜想v′.如果v′=v，挑战者B会输出μ′=0表示它是一个DBDH四元组.否则，它是一个随机四元组.

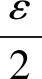
证毕.

4.2.1.2 可验证性安全

定理2.假设H0和H1抵抗合谋攻击的Hash函数，那么VDC-KP-ABE方案具有可验证性.

证明.

假设：若攻击者A可以攻破本文方案的可验证性，那我们就能创建一个挑战者B能够以不可忽略的优势攻破Hash函数的抵抗合谋攻击特性.

初始化：攻击者提交2个Hash函数(H*0,H*1).

系统建立：挑战者执行Setup阶段，然后用(H*0,H*1)替换公钥中的(H0,H1).

阶段1：B按照方案算法生成方式适应性回答攻击者A的询问.

挑战阶段：攻击者A提交一个密文M*和一个访问策略A*，挑战者运行Enc算法获得密文CT*和验证VK*.

阶段2：B按照方案算法生成方式适应性回答攻击者A的询问，攻击者不可以询问属于访问策略A*的属性.

猜测阶段：攻击者A输出转换密文CT*part=(C1,B).

若攻击者A攻破可验证性，则挑战者B可以从Decryptin(CT*part,RK*,VK*)恢复出明文.

计算攻击者A成功的概率，只需考虑2种情况：

① (H0(R),C1)≠(H0(R)*,C*1)，因为B知道(H0(R)*,C*1)，则B得到Hash函数H*1的碰撞值.

② (H0(R),C1)=(H0(R)*,C*1)，但R≠R*，因为H*0(R)≠H*0(R*)，则H*0抗合谋性将被攻破.

综上所述，完成定理2的证明.

证毕.

4.2.2 效率

本节从理论上分析密钥生成、加密过程和解密过程的计算开销，将本文构造方案与文献[3,6,13]中方案进行计算效率对比.其中，E表示G中指数计算，P表示对计算，M表示群乘法计算.另外W表示属性集的大小，d表示陷门值，l表示线性秘密共享(LSSS)中生成矩阵的行数.指数、群乘法运算和双线性对的计算量相对于其他计算需要更多的计算时间，因此本文忽略了次要因素.

本文方案和文献[3,6,13]中方案的效率对比如表2所示.文献[3]中是原始ABE方案，与文献[3]中方案对比，本文方案将密钥分配和解密工作外包，并且可验证外包结果正确性，同时用户计算量减少，缓解了资源受限用户的计算负担问题，加快了方案运行效率，且支持属性撤销与用户追踪.与文献[13]方案相比，本文方案支持外包计算的可验证性，且计算效率更高.与文献[6]中ABE方案相比，本文构造的方案使用线下加密，既减少线上加密时间、加快方案效率，又有效保护用户数据的安全性，同时支持属性撤销和用户可追踪.

Table 2 Comparison of Efficiency

Note: The tick indicates that this function is supported in the article, and the cross indicates that this function is not supported in the article.

5 总 结

为了满足计算、存储能力不足用户的访问需求，本文构造了将密钥分配和解密过程外包的属性加密方案，并且能够验证外包计算的正确性.该方案支持属性撤销，并且可追踪泄露密钥的用户.本文方案应用树形访问策略，达到更细粒度的访问控制；其次方案将加密过程分为在线阶段和离线阶段，离线阶段利用已知的公钥进行部分加密，既有效保护用户数据的隐私性，又减轻了用户的计算负担；针对实际应用中用户访问权限的变更，本文方案通过使用重加密的方法更新密文与密钥，支持基于访问树的细粒度属性撤销，并将用户身份嵌入到用户密钥中，既防止合谋攻击，又可以通过密钥追踪到用户身份.最后，在标准模型下基于DBDH假设证明了本文方案是IND-CPA安全的.