云南省水安全区域类型识别TSA-PP模型及应用

李杰 崔东文

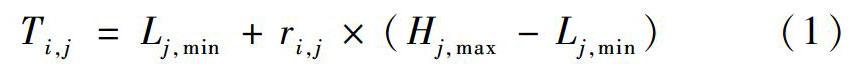
摘要：为科学识别云南省16个州市的水安全区域类型，提出了树-种算法（TSA）-投影寻踪（PP）识别模型。选取了4个典型测试函数对TSA进行仿真验证，并将验证结果与人工蜂群（ABC）算法、布谷鸟搜索（CS）算法等6种算法的仿真结果进行了对比。以云南省为研究对象从水资源条件、经济社会条件和水环境条件中遴选出了27个指标构建区域水安全类型识别指标体系和分级标准，在各分级标准阈值间采用随机内插的方法生成样本;同时，构建了基于水资源、经济社会和水环境条件的投影指标函数，并分别采用TSA搜索最优投影向量，计算云南省内各州市的综合投影值以及各分级标准阈值的投影值，然后利用分级标准阈值投影值对各行政区的水安全区域类型进行识别。结果表明：TSA寻优精度优于ABC、CS等6种算法，具有较好的收敛精度、极值寻优能力和收敛稳健性能。TSA-PP模型对云南省各州市的水安全类型识别结果为：昆明市、玉溪市为“中度缺水-较发达-中等”型;楚雄州、大理州为“严重缺水-中度发达-较差”型;西双版纳、迪庆州为“中度缺水-中度发达-中等”型;丽江市为“严重缺水-中度发达-中等”型;德宏州为“轻度缺水-中度发达-中等”型;怒江州为“轻度缺水-中度发达-较差”型;其他州市被识别为“中度缺水-中度发达-较差”型。

关键词：水安全; 区域类型; 指标体系; 树-种算法; 投影寻踪; 云南省

中图法分类号：P33文献标志码： ADOI：10.16232/j.cnki.1001-4179.2019.02.011

1研究背景

水安全是指一个国家或区域在一定时期、一定技术水平和经济社会发展条件下，水资源、水环境能够支撑其经济社会的持续发展、维护生态系统良性循环的状态。从水资源角度上来说，水安全是指区域水资源量及其供给能力能否满足人类生存与社会发展所需的稳定、持续、及时与足量的水量与供给能力;从经济社会可持续发展的角度上来说，水安全是指区域水资源量能够保障该区域的社会经济当前的需求，同时又不影响当地可持续发展的状态和能力;从水环境水生态角度上来说，水安全是指水环境与水生态质量支撑区域经济社会发展的综合承载能力[1]。

云南省地处祖国的西南边陲，下辖昆明、曲靖等16个州（市），国土面积为39万km 分属长江、珠江等六大水系;多年平均降水量为1 279 mm，水資源总量为2 222亿m 3，仅次于西藏、四川两省区，居全国第三位。由于横断山脉深度切割，高差悬殊，地形地貌复杂，云南省水资源总量虽然丰富，但其开发利难度大、成本高、边际效益低，加之特殊的地形环境和气候条件，降水时空分布极不均匀，从而造成了区域间经济社会发展不平衡，水资源、水环境状况差异明显。近些年来，随着云南省经济社会的飞速发展、城镇化和工业化进程的加快，水资源短缺、水环境污染等问题日益突出，水安全问题面临着严峻的挑战。

水安全评价研究起步于20世纪70年代，主要评价方法有层次分析法[2-3]、物元分析法[4]、水贫困指数法[5]、逻辑斯蒂曲线法[6]、概率神经网络法[7]、支持向量机法[8]、模糊集对分析法[9-10]，以及最大熵投影寻踪法[11]等。为了进一步拓展水安全评价方法，本文融合树-种算法（tree–seed algorithm，TSA）与投影寻踪（projection pursuit，PP）技术，构建了TSA-PP区域水安全评价模型，并将其用于对云南省16个州（市）的水安全进行评价。本文主要研究内容包括：

（1） 介绍一种新型群体智能算法——树-种算法（TSA），选取4个标准测试函数对TSA进行仿真测试，并与人工蜂群（ABC）算法、布谷鸟搜索（CS）算法、混合蛙跳算法（SFLA）、文化算法（CA）、粒子群优化（PSO）算法和蚁群优化（ACO）算法的性能进行对比。

（2） 基于水资源条件、经济社会条件和水环境条，遴选出了27个指标来构建水安全区域类型识别指标体系和分级标准。

（3） 利用TSA优化PP技术最佳投影方向，构建TSA-PP水安全区域类型识别模型，来对云南省所辖州（市）的水安全进行评价分析。

2树-种算法及验证

2.1树-种算法

树-种算法（TSA）是K1ran M. S.于2015年通过模仿大自然中的树-种子繁衍行为而提出的一种新型的群体启发式搜索算法[9]，该算法具有模型简单、调节参数少、收敛精度高等优点，参见参考文献[12]。TSA的数学描述如下。

（1） 初始化。在自然界中，树通过种子传播到地上，种子随着时间而生长成新树，新树又通过种子传播进行繁衍生息。假设将树群地面范围作为待优化问题的搜索空间，则树和种子的空间位置可被视为待优化问题的候选解（这里将产生种子的树称为父树）。文献[13] 利用式（1）获得了待优化问题候选解的初始化树空间位置。

Ti，j=Lj，min+ri，j×（Hj，max-Lj，min）（1）

式中，Ti，j表示第i棵树的第j维;Hj，max，Lj，min分别表示搜索空间的上、下限;ri，j表示[0，1]范围内的每个维度和位置随机数。

（2） 更新机制。TSA中每棵树产生种子的数量完全是随机的，文献[14]分析表明，每棵树产生种子数量的上限和下限在树群的10%～25%之间具有较好的搜索效果。TSA利用式（2）和式（3）对种子进行更新。

Si，j=Ti，j+i，j×（Bj-Tr，j）（2）

Si，j=Ti，j+i，j×（Ti，j-Tr，j）（3）

式中，Si，j表示将要成长成父树的第i个种子的第j维;Ti，j表示第i棵树的第j维;Bj表示当前获得的最佳树的个体空间位置的第j维;Tr，j表示从树群中随机选择的第r棵树的第j维;表示[-1，1]范围内随机生成的缩放因子。

（3） 控制参数ST。TSA探索和开发能力由[0，1]范围内的ST参数进行控制。较大的ST可以使TSA获得较好的局部搜索能力和收敛速度;较小的ST会导致TSA收敛缓慢但可获得较好的全局搜索能力。

（4） 适应度值计算。对于最小值优化问题，利用式（4）可从群体中获得最优解。

B=min{f（Ti）}i=1，2，…，N（4）

式中，N表示树群的数量。

2.2仿真验证

为了验证TSA优化性能，实验选取了4个典型测试函数进行仿真测试，并与ABC，CS，SFLA，CA，PSO和ACO算法进行性能对比。实验标准测试函数如表1所示，其中，f1为单峰连续优化函数，用于测试算法的收敛速度和寻优精度;f2～f4为多峰连续函数，存在许多局部极值，用于测试算法逃离局部极值和全局探索能力。

算法参数设置为：TSA最大迭代次数L=1 000，种群规模算法N=50，控制参数ST=0.1;ABC算法最大迭代次数L=1 000，种群规模N=50，局部循环次数lc=60;CS算法最大迭代次数L=1 000，鸟窝位置数n=25，发现概率pa=0.25;SLFA最大迭代次数L=1 000，青蛙群体规模N=50，子群数K=5，子群内青蛙个数Np=10;子群数局部进化次数T1=10;CA迭代次数L=1 000，群体规模N=50，根据标准知识产生的群体规模N′=50;PSO算法最大迭代次数L=1 000，种群规模N=50，ω=0.729，局部学习因子、全局学习因子c1=c2=2.0;ACO算法最大迭代次数L=1 000，群体规模N=50，常量Q=1，信息素挥发系数ρ=0.4。

基于Matlab 2010a，7种算法用M语言实现，对表1中的每个测试函数独立运行20次，并统计平均最优适应度值（MBF）和标准差（SD）的结果，详见表2。其中，MBF反映的是算法在运行至最大迭代次数时可以达到的求解精度，SD则是反映算法的收敛稳定性。

从表2可以得出：对于函数f1，TSA和SFLA均获得了较好的收敛精度，精度高于其他5种算法的71个数量级以上，其中，TSA收敛精度略优于SFLA。对于函数f2，TSA收敛到全局最优解0，寻优精度远远高于其他6种算法。对于函数f3，TSA、ACO和CS算法均获得了较好的寻优效果，精度高于其他4种算法的5個数量级以上，其中，TSA寻优精度高于ACO和CS算法。对于函数f4，TSA和ACO算法寻优精度相同，精度高于其他5种算法的9个数量级以上。整体比较而言，7种算法对于4个标准测试函数的优化性能的寻优效果从优至劣依次是：TSA、ACO、CS、SFLA、ABC、CA和PSO。

可见，对于单峰或多峰函数，TSA均表现出了较好的寻优精度、逃离局部极值能力和收敛稳健性能。

3水安全区域类型识别指标体系

笔者以云南省16个州市的水安全区域类型识别为例，在充分考虑区域水资源条件、经济社会发展水平和水环境条件3个方面的前提下，参考了文献[5，7-8，15]并构建了具有云南省区域特征的水安全类型识别指标体系和分级标准，如表3所示。同时，综合考虑到云南省现阶段的水资源、经济社会以及水环境现状等因素，拟定了现状条件下的水安全区域类型识别指标在各分级的范围，并依据各州市及分级阈值的最大值、最小值上下浮动20%来确定各指标的上下限值，对于C20～C22指标，则以“100”作为其上限值。

4TSA-PP水安全类型识别模型

4.1投影寻踪模型

PP技术是通过数学方法将高维数据投影到低维空间，在低维空间进行数据分析以获取评价指标最优空间投影向量，目前已在水量分配[14]、洪旱灾害评估[13]、水资源利用效率[15-16]、水土保持效益评价[17]、洪水分类[18-19]以及水污染物分配[20]等方面得到了应用。PP技术简要算法如下[15，21]。

（1） 数据预处理。对于正向、负向指标，分别采用式（5）和式（6）进行处理。

x（i，j）=[x（i，j）-xmin（j）]/[xmax（j）-xmin（j）]（5）

x（i，j）=[xmax（j）-x（i，j）]/[xmax（j）-xmin（j）]（6）

式中，x（i，j）为指标特征值归一化序列;xmax（j），xmin（j）分别为第j个指标值的上、下限值。

（2） 构建投影值指标函数。

z（i）=mj=1a（j）x（i，j）（7）

式中，a为单位长度向量。

（3） 模型求解。将搜寻最优投影向量问题转化为单目标非线性最优求解问题，即：

max：Q（a）=SzDz

s.t：mj=1a 2（j）=1a∈[-1，1]（8）

式中，SZ为投影值z（i）的标准差;DZ为投影值z（i）的局部密度。SZ，DZ表达式参见文献[14];Q（a）即本文待优化目标函数QW（a），QS（a）和QE（a）。

4.2 TSA-PP模型识别实现步骤

Step 1。依据表3，在评价指标标准阈值间随机生成10组数据样本，共随机生成了50组数据样本，利用式（5）和式（6）对样本进行一致性处理。

Step 2。利用一致性处理后的样本，分别构建基于水资源条件、经济社会条件、水环境条件的投影指标函数QW（a），QS（a）和QE（a）。利用TSA对QW（a），QS（a）和QE（a）投影向量进行优化求解。

Step 3。设置树群规模N、问题维度D、最大迭代次数L、当前迭代次数l、控制参数ST，利用式（1）初始化树群D维空间位置，确定随机产生每棵树的种子数量。

Step 4。利用适应度函数计算树群中每棵树的适应度值并进行比较，根据适应度值确定当前最佳父树空间位置。

Step 5。利用适应度函数计算种子个体的适应度值。若当前最佳种子适应度值优于父树适应度值，则将父树从树群中移除，当前种子保存成父树，并保留当前位置为最优个体空间位置;否则保留前代父树位置为最优个体空间位置。

Step 6。若[0，1]范围内随机产生的数字小于控制参数ST，则利用式（2）更新维度，否则利用式（3）更新维度。

Step 7。令l=l+1，判断算法是否达到终止条件，若是，输出最佳树个体空间位置，算法结束;否则重复Step5～Step5。

Step 8。分别输出最佳树个体空间位置，即最佳投影向量aW，aS，aE。

Step 9。利用式（5）和式（6）对云南省各州市指标数据及分级标准阈值进行一致性处理，利用最佳投影向量aW，aS，aE分别计算各州市的综合投影值zW（i），zS（i），zE（i）以及各分级标准阈值的投影值zW（k），zS（k），zE（k）（k=5，为水安全区域类型识别分级数）;同时，利用zW（k），zS（k），zE（k）对各州市的水安全区域类型进行识别。

5实例应用

5.1模型构建与求解

（1）数据来源。本文研究数据来源于《2015年云南省水资源公报》《2015年云南省统计年鉴》等，限于篇幅从略。

（2）优化目标函数构建。基于表3，并依据TSA-PP水安全区域类型识别模型实现步骤，利用随机生成并经过一致性处理的样本，分别构建水安全区域类型识别投影目标函数QW（a），QS（a）和QE（a）;借助于TSA，对最佳投影向量aW，aS，aP分别进行优化求解。TSA参数的设置，除了最大迭代次数L=100外，其余参数的设置同上。

（3）模型求解。本文TSA采用Matlab 2010a以

M语言实现，分别对投影目标函数QW（a），QS（a）和QE（a）独立运行20次，并分别统计平均适应度值Q（a）、标准差（SD）以及平均投影向量a，如表4所示。TSA在目标函数QW（a），QS（a）和QE（a）上的前5次进化过程图如图1所示。

从表4及图1可以看出，TSA在投影目标函数QW（a），QS（a）和QE（a）上连续运行20次的SD精度均在4.02×10-4以上，表明TSA具有较好的求解精度和稳健性能。

5.2评价结果与分析

依据TSA-PP水安全区域类型识别模型实现步骤，將云南省16个州市的指标数据按照公式（5）和公式（6）进行一致性处理;利用aW，aS，aE分别计算水资源条件、经济社会条件和水环境条件下的水安全区域类型识别分级标准zW（k），zS（k），zE（k）以及综合投影值zW（i），zS（i），zE（i）。详见表5～6和图2所示。由表6和图2可以得出以下结论。

（1） 从水资源条件方面来看，怒江州、德宏州识别为轻度缺水地区。怒江州虽然在16个州市中水资源利用率极低（仅为1.18%），降水量、人均水资源量最大，但是在单位面积水利实施供水能力和水库总库容占供水总量之比两个方面表现较差，识别为轻度缺水较合理。德宏州在降水量等水资源量方面表现突出，同时在供水量模数和单位面积水利实施供水能力两方面表现也较好，识别为轻度缺水较合理。丽江市、楚雄州和大理州水资源开发初具规模，同时在降水量、产水量模数等自然水资源量方面表现较差，识别为严重缺水地区较合理。将其他11个州市识别为中度缺水地区，或在天然水资源量方面表现较差，比如昆明市和玉溪市等;或在人工水资源量方面表现较差，比如迪庆、普洱等。从图2可以直观看出，德宏州的水资源条件投影值最大，为1.597 6，楚雄州最小，为0.721 7。

（2） 从经济社会条件方面来看，昆明市、玉溪市被识别为较发达;其他14个州市被识别为中度发达。从图2可以直观看出，昆明市的经济社会条件投影值最大，为2.290 0，怒江州的投影值最小，为1.261 4。

（3）从水环境条件方面来看，16个州市的水环境质量状况表现均不容乐观，识别等级在中等-较差之间。其中，昆明市、玉溪市、丽江市、西双版纳州、德宏州、迪庆州被识别为中等，其他10个州市被识别为较差。从图2可以直观看出，德宏州的水环境条件投影值最大，为1.768 2，昭通市的最小，为0.834 8。

（4）从水安全区域类型综合识别结果来看，昆明市和玉溪市的水安全区域类型被识别为“中度缺水-较发达-中等”型。昆明市是云南省的经济、政治和文化中心，经济社会较发达，玉溪市的人均GDP、城镇化率和人均纯收入仅次于昆明市，两市均属于较发达地区，但是在水资源、水环境两方面表现一般。通过加大水环境污染整治力度、提高城市污水处理及再生水的利用率，两市的水安全可以得到进一步提升，但是受限于天然水资源量，比如，降水量、人均水资源量及产水量模数等方面的制约，两市的水安全提升空间有限。

怒江州、德宏州的水安全区域类型分别被识别为“轻度缺水-中度发达-较差”型、“轻度缺水-中度发达-中等”型。通过发展经济，提高工业、农业用水效率，改善水环境质量等，水安全水平可以得到有效提升。尤其是怒江州，其城市污水处理率仅为36.1%，通过加大水环境污染整治力度、改造城市污水处理设施等，水安全水平将会得到大幅提升。

楚雄州、大理州的水安全区域类型被识别为“严重缺水-中度发达-较差”型，在水资源、水环境两方面均表现较差。通过加大水污染防治力度，提高污水处理率，改善水环境质量，其水安全水平可以得到进一步提升;但是受制于天然降水量、人均水资源量等的制约，其水安全水平提升程度有限。

丽江市的水安全区域类型被识别为“严重缺水-中度发达-中等”型，主要是在水资源方面表现较差。通过新建水利工程，提高供水量模数和水库总库容占供水总量之比，其水安全水平可以得到提升。

西双版纳州、迪庆州的水安全区域类型均被识别为“中度缺水-中度发达-中等”型，就是在水资源、经济社会和水环境3个方面均表现一般。通过改善民生和发展经济，加大水源开发力度，提高供水能力和水资源利用效率，进一步改善城市环境质量，两个州的水安全水平将会得到较大提高。

其他州市，比如曲靖市、保山市等7个州市的水安全区域类型被识别为“中度缺水-中度发达-较差”型，均是在水环境方面表现最差。通过发展经济，加大水源开发力度，提高供水量模数及单位面积水利实施供水能力，尤其是通过加大水环境治理力度，改善水环境质量，则上述7个州市的水安全状况将会得到较大改善。

6结 论

（1） 介绍了一种新型群体智能算法——树-种算法（TSA），选取了4个标准测试函数对TSA进行仿真验证，并与ABC，CS，SFLA，CA，PSO和ACO算法进行性能对比，结果表明，TSA具有较好的寻优精度、逃离局部极值的能力和收敛稳健性能。

（2） 综合考虑到云南省区域水资源、经济社会和水环境条件，提出了具有区域特征的水安全区域类型识别指标体系和分级标准。在各识别指标标准阈值间随机生成数据样本，构造了基于水资源、经济社会和水环境条件的投影目标函数;同时，利用TSA搜索各目标函数的最佳投影向量。指标体系、分级标准、数据样本生成方法及目标函数的构建方法，对区域水安全类型的识别或评价研究均具有一定的参考价值。

（3） 提出了TSA与PP相融合的TSA-PP水安全区域类型识别模型，以云南省16个州市的水安全区域类型识别为例进行验证。验证结果表明，TSA-PP模型用于水安全区域类型的识别是可行的也是有效的。

（4） 从实例水安全区域类型识别结果来看：① 昆明市、玉溪市为“中度缺水-较发达-中等”型;② 楚雄州、大理州为“严重缺水-中度发达-较差”型;③ 西双版纳州、迪庆州为“中度缺水-中度发达-中等”型;④ 丽江市为“严重缺水-中度发达-中等”型;⑤ 德宏州为“轻度缺水-中度发达-中等”型;⑥ 怒江州为“轻度缺水-中度发达-较差”型;⑦ 其他州市被识别为“中度缺水-中度发达-较差”型。

针对不同的水安全区域类型，通过分析，提出了水安全水平提升及改善的措施方法。

参考文献：

[1]刘斌涛，陶和平，孔博，等.云南省水资源时空分布格局及综合评价[J].自然资源学报，2014，29（3）：454-465.

[2]王彦威，邓海利，王永成.层次分析法在水安全评价中的应用[J].黑龙江水利科技，2007（3）：117-119.

[3]崔艳强，范弢，杨佳.云南省城市饮用水安全评价研究[J].人民長江，2011，42（7）：51-55.

[4]刘传旺，吴建平，任胜伟，等.基于层次分析法与物元分析法的水安全评价[J].水资源保护，2015，31（3）：27-32.

[5]贡力，靳春玲.基于水贫困指数的城市水安全评价研究[J].水力发电学报，2014，33（6）：84-90.

[6]宋培争，汪嘉杨，刘伟，等.基于PSO优化逻辑斯蒂曲线的水资源安全评价模型[J].自然资源学报，2016，31（5）：886-893.

[7]汪嘉杨，刘韵，李祚泳，等.基于指标规范化概率神经网络的水安全评价模型[J].水力发电学报，2014，33（6）：78-83.

[8]汪嘉杨，王文圣，李祚泳，等.基于TS-SVM模型的水安全评价[J].水资源保护，2010（2）：1-4.

[9]沈俊源，吴凤平，于倩雯.基于模糊集对分析的最严格水安全综合评价[J].水资源与水工程学报，2016，27（2）：92-97.

[10]王子茹.基于可变模糊集对立统一定理的水安全评价研究[J].人民长江，2011，42（9）：1-3.

[11]苏敏杰，白栩嘉.NBA-MEPP模型在区域水资源安全评价中的应用[J].人民长江，2017，48（13）：36-42.

[12]Klran M S.TSA：Tree-seed algorithm for continuous optimization[J].Expert Systems with Applications，2015，42（19）：6686-6698.

[13]崔东文.鸡群优化算法投影寻踪洪旱灾害评估模型[J].水利水电科技进展，2016，36（2）：16-23.

[14]崔东文，金波.基于新型蝙蝠算法-投影寻踪模型的文山州水量分配方法[J].水利水电科技进展，2017，37（2）：55-62.

[15]白栩嘉 苏敏杰.基于改进PSO-PP模型的区域水资源利用效率评价[J].人民长江，2016，47（23）：38-43.

[16]崔东文.文山州近10年水资源利用效率评价SLC-PP模型及应用[J].河海大学学报：自然科学版，2017，45（2）：129-136.

[17]徐昕，李杰，陈芳，等.基于WPAPP模型的水土保持综合效益研究[J].人民长江，2017，48（12）：79-83.

[18]张雅琦，李妍清，戴明龙，等.基于投影寻踪法的三峡入库洪水与坝址洪水分类[J].人民长江，2016，47（9）：25-28.

[19]汪丽娜，陈晓宏，李粤安.投影寻踪和人工鱼群算法的洪水分类[J].人民长江，2008，39（24）：34-37.

[20]崔东文.正弦余弦算法-投影寻踪水污染物总量分配模型[J].水资源保护，2016，32（6）：75-81.

[21]崔东文，郭荣.SSO-PP模型在水源地安全保障达标评价中的应用[J].水利经济，2015，33（5）：8-13.

引用本文：李杰， 崔东文.云南省水安全区域类型识别TSA-PP模型及应用[J].人民长江，2019，50（2）：58-64.

TAS-PP model and its applications in identifying water security zone type in Yunnan Province

LI Jie ，CUI Dongwen 2

（1.Yunnan Water Conservancy and Hydropower Survey and Design Institute， Kunming 650021， China;2.Wenshan Water Bureau of Yunnan Province， Wenshan 663000，China）

Abstract： TSA-PP identification model （tree-seed algorithm and projection pursuit） was proposed to scientifically identify the water security zone of sixteen prefectures in Yunnan Province. We selected four typical test functions to simulate TSA， and compared it with the results obtained by other six algorithms including ABC algorithm and CS algorithm. We chose twenty-seven indicators from water resources condition， economic and social conditions and water environment condition to construct the regional water safety type identification index system and grading standard. Random interpolation method was used to get samples between the thresholds of each classification standards; meanwhile， based on the three aforementioned conditions， projection indicator function was constructed. TSA was used to search the optimal projection vector. The comprehensive projection value of each prefecture and the threshold value of each grading standard were calculated. The graded standard threshold projection value was employed to identify the water area of each prefecture. The results show that TSA is superior to ABC and CS algorithm， and it has good abilities in convergence accuracy， extreme value search and convergence performance. The results （denoted by “water stress condition- economic/social condition- water environment condition） obtained by TSA-PP model are as follows： Kumming and Yuxi are “moderate-developed-moderate” type; Chuxiong and Dali prefectures are “severe-moderate developed-poor” type; Xishuangbanna and Diqing prefectures are identified as “moderate-moderate developed-moderate” type; Lijiang is “severe-moderate-moderate” type; Dehong prefecture is “mild-moderate developed-moderate” type; Nujiang prefecture is “mild-moderate-poor” type; other prefectures are “moderate-moderate developed-poor” type.

Key words：water safety; water security zone type; index system; tree-seed algorithm; projection pursuit; Yunnan Province