水平轴潮流能水轮机叶片变桨角度研究

摘要：利用Flow-3D软件建立了单桩型水平轴潮流能发电机的三维数值模型。采用该模型对不同叶片变桨角度时的水动力过程进行了模拟计算，并根据计算结果从叶轮转速、叶轮动能、叶轮受力、水位和流速变化的角度进行了分析和讨论。数值模拟结果表明：当叶片变桨角度增大时，来流方向的叶轮受力和叶轮动能也都随之增大;变桨角度对于与来流垂直的y和z方向的叶轮受力影响较小;叶片变桨角度越大、水轮机下游附近流速降低的越快，流速就越小，而在水轮机下游较远处，叶片变桨角度越大，尾流场恢复得越快，其流速也越大。

关键词：潮流能;三维数值模拟;叶片变桨角度;水轮机;水动力特性

中图法分类号：TV734

文献标志码：A

DOI：l0.16232/j.cnki.1001-4179.2019.03.036

1研究背景

能源是人类赖以生存和经济发展的重要物质基础，近年来，随着我国社会经济的快速发展，对能源的需求也日益增长。潮流能由于具有能量密度大、储量丰富、规律性强以及载荷稳定等特点而越来越受到世界各科技强国的关注和重视[1-5]。潮流能发电系统的核心组成部分是潮流能发电机组，目前由于其能量提取率高、技术成熟稳定，水平轴潮流能发电机组成为了应用较广的机型[6-9]。对于水平轴潮流能机组而言，开展潮流能水轮机叶轮变桨角度对叶轮水动力响应影响方面的研究，可以为水轮机控制系统设计提供重要的参考依据。

李志川等人[10]对CFD技术在潮流能发电中的应用情况进行了介绍，并指出：随着计算机技术及计算数学技术的发展，CFD必将逐步成为研究潮流能发电的主要手段。袁金雄[11]借助于数值模型，对不同推力系数条件下的尾流场的变化规律进行了模拟分析，结果表明：推力系数对尾流场具有显著的影响，随着推力系数的逐渐增大，尾流流速和尾流流速的恢复速度都随之减小。Li等[12]对单台单桩式水平轴潮流能机组周边的流场分布特性進行了研究。辛小鹏等人[13]采用数值模拟开展了研究，模拟结果表明：当上下游水轮机纵向间距在5D（5倍叶轮直径）以内时，上游机组的尾流对下游机组发电效率的影响较大;当纵向间距增大到30D时，尾流对发电效率的影响能显著减小到可忽略的程度。谭俊哲等人[14]采用数值模型，研究了海底地形变化对潮流能水轮机水动力响应的影响。Mal-kiR等[15]借助于数值模型，对潮流能水轮机发电效率与间距之间的关系进行了模拟分析。StallardT等人[16]通过采用模型试验的方法，对潮流能水轮机组尾流场的空间分布特点和尾流影响区域等进行了研究。MacLeodAJ等人[17]采用数值模型，分析了潮流能水轮机叶轮安装高度和叶轮轴向推力系数等因素对尾流场的影响。安佰娜[18]采用数学模型，对0～35D范围内逐渐增加上下游潮流能水轮机间的纵向间距进行了模拟分析，从而得到了不同纵向间距下水轮机间的影响规律;同时，还对潮流能水轮机不同布置形式时的流速、压强和紊流等水动力要素的分布规律进行了对比分析。

目前，国内外对于水平轴潮流能机组的研究，主要还是集中在潮流能机组尾流场空间的分布及多机组相互影响规律的研究上，而对于叶片变桨角度方面的研究则相对较少。对于上述问题，本文采用三维计算流体动力学软件Flow-3D，针对单桩式水平轴潮流能发电机组，模拟分析了叶片变桨角度对叶轮受力、叶轮获能效率和尾流场等产生的影响。

2数学模型

在进行数值模拟时，是以N-S方程为控制方程进行水动力模拟的。运用GMO模块来模拟刚体在流体内的运动状况，即刚体与流体间的流固耦合运动;采用FAVOR方法，利用简单的矩形网格来表示叶轮复杂的几何形状。

2.1水流控制方程

以N-S方程作为流体运动控制方程，应用流体体积法（VOF）[19]，来跟踪处理自由水面;采用大涡模拟（LES）方法来模拟紊流运动。质量连续方程为

公式

式中，VF为流体在网格单元内所占的体积百分，%;t为时间，s;p为流体密度，kg/m3;RSOR为质量源项;RDIF为扩散项;Ax，Ay，Az分别为流体在x，y，z方向所占的面积百分比，%;u，v，w分别为流体在x，y，z方向的速度分量。

x，y，z方向上的动量守恒方程可以分别以如下形式表示：

公式

式中，Gx，Gy，Gz分别为重力加速度在x，y，z方向的分量;uw，vw，Ww。分别为与运动物体有关的速度源项;fx，fy，fz分别为黏性力在x，y，z方向的分量;us，vs，ws分别为与运动物体有关的相对质量源项界面的流体速度，m/s;δ为质量源的压力类型，本文中δ取1，表示为静态压力类型的质量源，此时根据质量源的表面积和流量来计算流体的速度，而不需要提供额外的压力使流体从质量源中流出。

2.2FAVOR方法

FAVOR方法[20]是GMO模块的核心组成部分。

它利用简单的矩形网格来表示潮流能机组，特别是叶片的几何外形、运动和位置，以及机组与黏性流体间的流固耦合。其控制方程如下：

公式

式中，Vf为流体在网格单元内所占的体积百分比，%;A为流体在网格单元内所占的面积百分比，%;Sm为流体质量源项。

2.3模型验证

目前，该模型已被成功地应用于单桩式水平轴潮流能水轮机水动力性能的数值模拟研究[21]。本文将使用该模型，针对不同叶片变桨角度对水平轴潮流能水轮机的水动力特性的影响开展分析研究，研究结果可为潮流能水轮机叶片变桨控制系统的开发提供一定的科学依据。

2.4模型建立

潮流能水轮机叶轮的初始旋转速度为0，将初始水深设置为50m，水体的上边界取自由表面，不考虑其表面张力，水槽两侧为光滑的固体壁面边界，以表面粗糙度为5的固定海床为底边界。

当使用Flow-3D热启动功能的时候，首先需要利用Flow-3D软件建立一个与目标工况水深和宽度相同且足够长的数值水槽，将通过足够长的时间获得边界层充分发展的水流作为目标工况水槽中水的初始状态;然后结合“GridOverlay"边界提供一个稳定的进口流速条件。在本文模拟中，数值水槽长、宽和水深分别为300，100m和50m。根据具体算例，对x，y，z方向上的网格尺寸进行调试，网格整体布局原则是：在研究者关注的桩基础和叶轮等重要位置进行局部加密，而在其他位置则可以适当调大尺寸。总体上而言，所选网格尺寸需要既能保证精确反映叶轮的几何外形以及潮流能机组附近流场的分布，又要能保证计算效率网格不能太密。

在选择水轮机型号的时候，本文参照了舟山潮流能示范工程的实际情况，在本文三维数值模拟中：将叶輪叶片直径选为19m，扇叶倾角（叶片平面与叶轮旋转轴的夹角）分别为50°，60°和70°，将叶轮密度选为2700kg/m3，采用直径3m的圆柱为桩基础。

3叶片变桨角度的影响效应

为了研究叶片变桨角度对水轮机周边流场和水轮机水动力响应的影响，在三维数值模型中（如图1和图2所示），考虑了3种不同的叶片变桨角度（如图1所示，叶片变桨角指扇叶与旋转轴的夹角，图中为70°），分别为50°，60°，70°，在3种不同的变桨角度下，水轮机安装高度不变，均设为30m，水深均为50m。

3.1对叶轮转速和动能的影响

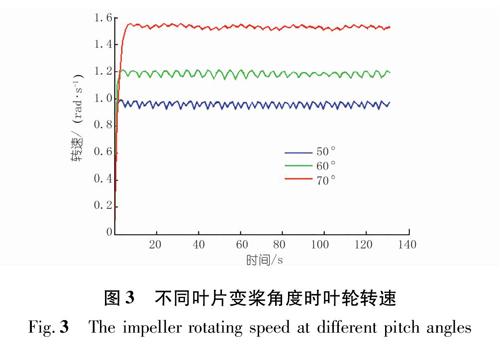
如图3所示，图中横纵坐标分别表示时间和叶轮转速，在来流作用下，潮流能水轮机叶轮转速在很短的时间内均由静止达到了相对平衡的状态。在不同叶片变桨角度时，水轮机从静止到相对平衡状态所需时间有微小差别，变桨角度增大时，叶轮达到平衡状态所需时间也略有增加。当变桨角度分别为50°，60°和70°时，对应的叶轮平均转速分别为0.96，1.18，1.51rad/s。变桨角度越大，叶轮转速越快，相应地从流场中获取的平均动能也越大。

如图4所示，图中横纵坐标分别表示时间和叶轮转动的动能，当变桨角度为50°时，其平均转动动能约为1.08x106J。而当变桨角度增大到60°时，其平均动能增大到1.66x106J，增幅为53.7%。随着变桨角度的进一步增大，当变桨角度为70°时，其平均动能约为2.63x106J，增幅为58.4%。

模拟结果表明：叶片变桨角度对叶轮可获取的最大能量有着显著影响。在本文模拟的叶片变桨角度范围内，叶片变桨角度每增加10°，叶轮动能约增加55%。

3.2对水轮机各向受力的影响

如图5所示，图中横纵坐标分别表示时间和叶轮的受力，叶片变桨角度对潮流能机组叶轮受力具有显著影响。增加变桨角度会增加叶轮在来流方向（x轴方向）的投影面积，从而增加叶轮在来流方向（x轴方向）受到的水流作用力。由图5可以看出，当变桨角度分别为50°，60°和70°的时候，叶轮在x方向的受力平均值分别为7.88x105，1.22x106N和2.00x106N。变桨角度从50°增加到60°时，叶轮x方向受力的平均值增加了54.8%;从60°增加到70°时，该力增加了63.9%。在y方向和z方向上，变桨角度的增加对叶轮受力影响较小。

在对叶轮进行受力分析时，从工程的实际角度考虑，表1中分析了整个模拟过程中各向最大的水流作用力。

随着变桨角度的增大，x方向最大的水流作用力显著增大，而y方向和z方向的最大水流作用力均减小了，可能的原因是随着变桨角度的增加，叶轮在x方向的投影面积增大，而在y和z方向的投影面积减小了。在x方向，当变桨角度由50°逐渐增加到60°和70°时，Fx则由9.38x106N逐渐增加到1.43x106N和2.25x106N，增幅分别为52.5%和57.3%。在y和z方向上，F，值总为负数，即沿y轴负方向，这是由于叶轮转动的不对称性而引起的。随着变桨角度的增大，y和z方向的最大水流作用力均减小了，这是由于叶轮在y和z方向的投影面积减小了，从而导致这两个方向的总水流作用力减小。

3.3对水轮机尾流场和自由液面的影响

本章节将针对叶片变桨角度对潮流能水轮机附近自由液面和流速分布形态的影响展开分析。

为了清晰地对比叶片变桨角度对自由水面的水位线沿程变化规律的影响，图6给出了水轮机中心z剖面水位线变化图，图中横坐标为x坐标与叶轮直径D的比值，水轮机位于X/D等于零处;纵坐标表示水轮机放入前后水面变化的程度：相对于水位为正值时，表示水位壅高，为负时表示水位下跌。

从图6中可以看出，对于不同的叶片变桨角度，水位线沿程变化规律总体，上是相同的，即水轮机上游（X/D为负值时）水位总是上升的，而下游（X/D为正值时）水位总是下降的。产生这种现象的原因是由于水轮机阻碍了水流的运动，从而造成了.上游水位壅高，下游水位下跌。

同时，由图6和表2还可以看出，叶片变桨角度对水轮机上下游水位的升降程度有着显著的影响。

（1）当叶片变桨角度为70°时，水轮机上游0.278D处（X/D=-0.278）有最大水位升高值为0.187m，水轮机下游0.995D处（X/D=0.995）的水位达最小值-0.112m。

（2）当叶片变桨角度为60°时，水轮机上游0.235D处的最大水位升高值为0.103m，水轮机下游0.517D处的水位最小值为-0.043m。

（3）当叶片变桨角度为50°时，水轮机上游0.235D处的最大水位升高值为0.060m，水轮机下游0.493D处的水位最小值为-0.030m。

由表2可以看出，当叶片变桨角度分别从50°增加到60°和从60°增加到70°时，水轮机上游的最大水位值分别增加了71%和82%。同时，水轮机下游的最小水位值分别下降了43%和160%。总体而言，叶片变桨角度越大，上下游水位升高和降低的程度就越显著，而且发生最高和最低水位值的位置距水轮机也越远。

图7所示为3种叶片变桨角度（50°，60°，70°）下的尾流场中沿水流方向水轮机中心线上流速的沿程分布曲线图。图中的横坐标为x坐标与叶轮直径D的比值，水轮机位于X/D等于零处，因此，在X/D等于零处流速曲线不存在。纵坐标λ表示流速时均值与来流速度的比值（无量纲值），入为正（负）时，表示流速方向与来流方向相同（相反）。

由图7可以看出，不同的叶片变桨角度时流速沿程变化的规律类似，上游来流流向水轮机时流速迅速减小，在水流通过水轮机后，尾流场中距离水轮机下游5D范围以内的流速有着显著的改变，在水轮机下游1D附近时，相对流速λ值为负，这表明水流会向与来流相反的方向流动而形成漩涡;此后，当水流逐渐远离水轮机时，尾流场的流速逐渐恢复。

同时，通过对图7及表3中不同叶片变桨角度时的流速沿程变化情况进行对比，还可以看出：叶片变桨角度越大，水轮机下游附近流速减小的程度越大;但是，当逐渐远离水轮机时，流速恢复得却越快。具体模拟分析数据如下：

（1）在水轮机下游1D处，λ分别为0.21，-0.13和-0.25（分别对应50°，60°和70°的变桨角度）。

（2）水轮机下游2D处，λ分别为0.53，0.30和0.27（对应的变桨角度同上），在水轮机下游2D范围内最大叶片变桨角度为70°时，流速减小的程度最大，流速最小。

（3）水轮机下游3D处，λ分别为0.61，0.45和0.50（对应角度同上）。

（4）水轮机下游4D处，λ分别为0.64，0.53和0.62（对应角度同上），在水轮机下游3D至4D范围附近，最大叶片变桨角度70°对应的流速大于60°，同时小于50°

（5）水轮机下游5D处，λ分别为0.67，0.60和0.73（对应角度同上）。

（6）水轮机下游10D处，λ分别为0.77，0.82和0.88（对应角度同上）。

（7）水轮机下游15D处，λ分别为0.86，0.92和0.92（对应的角度同上），在水轮机下游距离大于5D处，最大叶片变桨角度70°对应的流速最大。

4结论

本文借助于三维水动力软件Flow-3D建立了数值模型，并运用该数值模型对于在均匀来流作用下的水平轴潮流能水轮机的水动力响应进行了模拟分析;同时，也对叶片变桨角度对水轮机转速和动能、水流作用力和尾流场的影响开展了研究。基于数值分析结果，可以得出如下结论。

（1）叶片变桨角度对叶轮转速和叶轮可获取的最大能量有着显著的影响。在本文模拟分析中，叶片变桨角度每增加10°，叶轮动能约增加55%。

（2）叶片变桨角度对叶轮x方向（来流方向）受力有着显著的影响。在本文模拟分析中，叶片变桨角度每增加10°，叶轮x方向的受力平均值约增加60%，最大值约增加55%;在y和z方向，变桨角度的增加对叶轮受力的影响较小。总体而言，随着变桨角度的增大，y和z方向的最大水流作用力略有减小。

（3）叶片变桨角度越大，水轮机下游附近（约2D范围内）的流速减小程度越大，尾流流速越小;同时，当水流逐渐远离水轮机时（约5D以外），较大的叶片变桨角度所对应的尾流恢复速度更快，而且尾流流速更大。

参考文献：

[1]Khan M J，Bhuyan G，lqbal M T，et al.Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines forriver and tidal applications：A technology status review[J].AppliedEnergy，2009，86（10）：1823-1835.

[2]Schonborn A，Chantzidakis M.Development of a hydraulic controlmechanism for cyclic pitch marine current turbines[J].RenewableEnergy，2007，32（4）：662-679.

[3]吴亚楠，武贺，封哲.普陀山-葫芦岛水道潮流能资源评估[J].可再生能源，2017，35（10）：1566-1573.

[4]阳婷.潮流发电试验场水动力特性数学模型研究[D].天津：天津大学，2015.

[5]姜宽舒，郭建斌，王江.波浪能发电装置液固耦合流体增频特性研究[J].人民长江，2014，45（4）：80-84.

[6]Haydar F H，Ahmed E S，Othman A K.Tidal current turbines glanceat the past and look into future prospects in Malaysia.Renewable andSustainable Energy Reviews[J].2012，16（8）：5707-5717.

[7]魏東泽，吴国荣，郭欣，等.潮流能开发技术研究进展[J].可再生能源，2014，32（7）：1067-1074.

[8]吴百公，朱挽强，陈健梅，等.水平轴潮流能发电机扭曲叶片和平直叶片的对比实验研究[J].太阳能学报，2018，39（1）：272-278.

[9]方海鹏，吴跃亮，张磊.波流作用下环行桩群结构局部冲刷试验研究[J].人民长江，2017，48（s1）：30-33.

[10]李志川，肖钢，张理，等.CFD技术在潮流能发电装置设计中的应用[J].应用能源技术，2013，36（1）：36-39.

[11]袁金雄.基于Fluent的潮流能提取水动力影响数值研究[J].人民黄河，2013，35（2）：125-127.

[12]LI Linjuan，ZHENG Jinhai，PENG Yuxuan，et al.Numerical investigation of flow motion and performance of a horizontal axis tidal turbine subjected to a steady current[J].China Ocean Engineering，2015，29（2）：209-222.

[13]辛小鵬，邵雪明，邓见，等，串列布置双转子海流机水动力性能预测[J].浙江大学学报：工学版，2011，45（7）：1227-1231.

[14]谭俊哲，李仁军，司先才，等.海底地形对潮流能水轮机水动力学性能影响数值模拟研究[J].海洋技术学报，2018，37（1）：94-101.

[15]Malki R，Masters I，Williams A J，et al.The influence of tidalstream turbine spacing on performance[C]// 9th European Waveand Tidal Energy Conference（EWTEC）.2011：3-9.

[16]Stallard T，Collings R，Feng T，et al.Interactions between tidal turbine wakes：experimental study of a group of3-bladed rotors[C]//Proceedings of 9th European Wave and Tidal Energy Conference（EWTEC），2011.

[17]MacLeod A J，Barnes S，Rados K C，et al.Wake effects in tidalcurrent turbine farms[C]// International conference on marine renewable energy-conference proceedings，2002：49-53.

[18]安佰娜.潮流能发电厂尾流场数值模拟及其多机组影响规律研究[D].青岛：中国海洋大学，2012.

[19]Barkhudarov M R.Lagrangian VOF Advection method for FLOW-3D[J].Flow Science Inc，2004，1（7）：1-11.

[20]Hirt C W，Sicilian J M.A porosity technique for the definition of obstacles in rectangular cell meshes[C]// Proceedings of Fourth Int.Conf.Ship Hydrodynamics，1985.

[21]Haydar F H，Ahmed E S，Othman A K.Tidal current turbinesglance at the past and look into future prospects in Malaysia[J].Renewable and Sustainable Energy Reviews，2012，16（8）：5707-5717.

引用本文：顾振华.水平轴潮流能水轮机叶片变桨角度研究[J].人民长江，2019，50（3）：205-210.

Study on influence of blade pitch angle on response of horizontal-axis tidal stream turbine

GU Zhenhua

（Shanghai Investigation，Design & Research Institute，Shanghai 200434，China）

Abstract：A 3D hydrodynamic model based on Flow-3D is developed in this paper for single pile horizontal-axis tidalstream turbine and the influences of the blade pitch angle on the impeller rotation rate，the impeller kinetic energy，the fluidforce，the water level and the flow velocity of the horizontal-axis tidal stream turbine are investigated by the model.Numericalanalysis results showed that：when the blade pitch angle increases，the fluid force on the impeller in the direction of the incomingflow and the impeller kinetic energy increases;the pitch angle has little effect on the impeller force perpendicular to the incomingflow direction;the larger the blade pitch angle is，the flow velocity in the downstream of the turbine declines more quickly andthe flow velocity is smaller;in far downstream of the turbine，the larger the blade pitch angle is，the faster the wake field recoversand the larger the flow velocity is.

Key words：tidal stream energy;3D numerical simulation;blade pitch angle;hydro turbine;hydrodynamic characteristic