高温作业专业服装设计

胡洋 陈程 韩书楠

摘   要：高温作业服是高温环境下工作的人们所必须穿着的服装。它主要由三层构成，每层都有隔热效果。高温作业服每层的厚度影响着它的性能。为了降低研发成本，缩短研发周期，每一层的最优厚度需要确定，这是本文所要研究的问题。对高温作业服的四层进行分析，建立每层的偏微分方程形式的热传导模型，求解温度分分布。引进确定决策变量，目标函数（衣服重量），约束条件，建立优化模型。运用Matlab软件，使用遗传算法找到满足约束条件的厚度的最优解。

关键词：高温作业专用服装  热传导模型  微分方程

中图分类号：TM-9                                 文献标识码：A                        文章编号：1674-098X（2019）04（c）-0139-02

在高温环境下工作时，人们需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，III层与皮肤之间还存在空隙，将此空隙记为IV层。为设计专用服装，将体内温度控制在37℃的假人放置在实验室的高温环境中，測量假人皮肤外侧的温度。由此来计算人体温度分布情况。

1  假人外侧温度随时间变化模型的建立

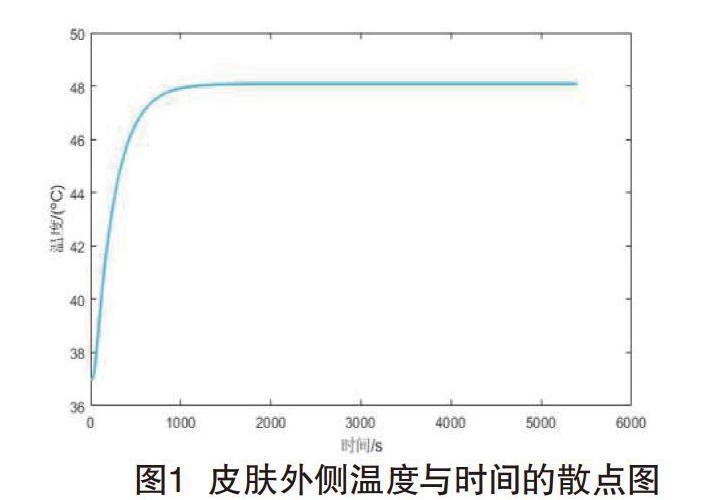
根据调查的数据绘制假人皮肤外侧温度与时间的散点图。如图1所示。

由图1可知：大约在0～1644s之间温度随着时间的增长呈现增长趋势，在1644s后，温度是一个定值，在0～1644s之间，时间与温度呈曲线关系。由于数据的变化趋势有明显变化，所以把数据分为2段进行处理。对0～1644s的数据用非线性回归的方法进行预测，后3600s的温度恒定。

为了更好的研究0～1644s的关系，运用SPSS对0～1644s的数据进行曲线拟合得到的拟合方程为：

由此可以得到环境温度为75℃的回归方程为：

当0

当t>1644时

2  温度分布模型的建立

在高温工作时环境向人体的传热过程简化为三步：

（1）环境向服装的第Ⅰ层传热。

（2）服装第Ⅰ层依次向第Ⅱ、第Ⅲ层传递。

（3）服装第Ⅲ层通过第Ⅳ层向人体传热。

以假人外侧某一点为原点，以该点的法线为y轴建立直角坐标系。在环境温度为75℃的情况下，建立热传导模型对各层进行分析[1]。

对于Ⅰ层，建立如下热传导模型：

其中：ρ1为Ⅰ层材料的密度，C1为Ⅰ层材料的比热容，T=（X，t）是t时刻坐标为x处的温度。t为处在高温环境下的时间，X为坐标。

引入过余温度：

因此，上式可整理为：

又因为初始条件为：

边界条件为：

通过以上公式，对于Ⅱ层建立热传导模型：

同理，对于Ⅳ层，建立热传导模型：

其中：

由以上各模型可得温度分布如图2所示。

3  热传导模型的建立

采用与1.2同样的方法，在环境温度为65℃的情况下，建立热传导模型对服装的各层进行分析。

对于Ⅰ层，建立如下热传导模型

其中：ρ1为Ⅰ层材料的密度，C1Ⅰ层材料的比热容，T2=T2（X，t）表示t时刻坐标为x处的温度，t为处在高温环境下的时间。

引入过余温度：

则上式可写为：

初始条件为：

边界条件为：

对于Ⅱ层，建立热传导模型

对于Ⅲ层，建立热传导模型

对于Ⅳ层，建立热传导模型：

其中：

，，。m为II层的厚度，单位为m。

4  建立II层厚度的优化模型

选取m为决策变量，且有：

根据题目中对高温作业专用服装的具体要求，要确保工作60min时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5min，由此建立约束条件。

为节省资源及提高服装的轻便性，将高温作业专用服装总重量作为目标函数。在单位表面积上II层的重量为：

（16）

所以，目标函数为：

由分析可知，满足约束条件

m的取值范围包含于[4，25]。引入遗传算法可得。

参考文献

[1] 卢琳珍，徐定华，徐映红.应用三层热防护服热传递改进模型的皮肤烧伤度预测[J].纺织学报，2018，39（1）：111-118，125.

[2] 苏云，王云仪，李俊.消防服衣下空气层热传递机制研究进展[J].纺织学报，2016，37（1）：167-172.

[3] 李志华，喻军，杨红光.偏微分方程与微分代数方程的一致求解方法[J].中国机械工程，2015，26（4）：441-445.

[4] 卢琳珍.多层热防护服装的热传递模型及参数最优决定[D].浙江理工大学，2018.

[5] 冯桂莲.偏微分方程的MATLAB数值解法及可视化[J].计算机技术与发展，2013，23（12）：120-123.