路堤荷载作用下软土硬壳层地基沉降计算

毛成琦，安泰莹，毛艳蕾

(1.山西省交通建设工程质量检测中心(有限公司) 太原市 030006； 2.北部战区海军保障部直属保障队 青岛市 266001； 3.人民解放军91206部队 青岛市 266108)

软土地基表面在光照和降水作用下，一般是非饱和的，压缩性低，强度高，在多次干湿循环作用下变得越来越“硬”，通常称之为软土硬壳层。

高等级公路对路基不均匀沉降要求严格，当公路穿越软土地区时，通常都是进行软基处理，忽略了硬壳层的整体性，增加施工成本和延长工期，如果能通过精确的地质勘查和理论计算，不对地基进行处理而又能保证在软土硬壳层上直接填筑路基的稳定性，将对工程设计有指导性意义。

1 研究背景及工程简介

在软土地区高等级公路建设中积累了大量的数据、资料，其中在软土硬壳层地区，有部分试验段路堤是直接填筑在原地面上的，其沉降观测数据统计见表1：

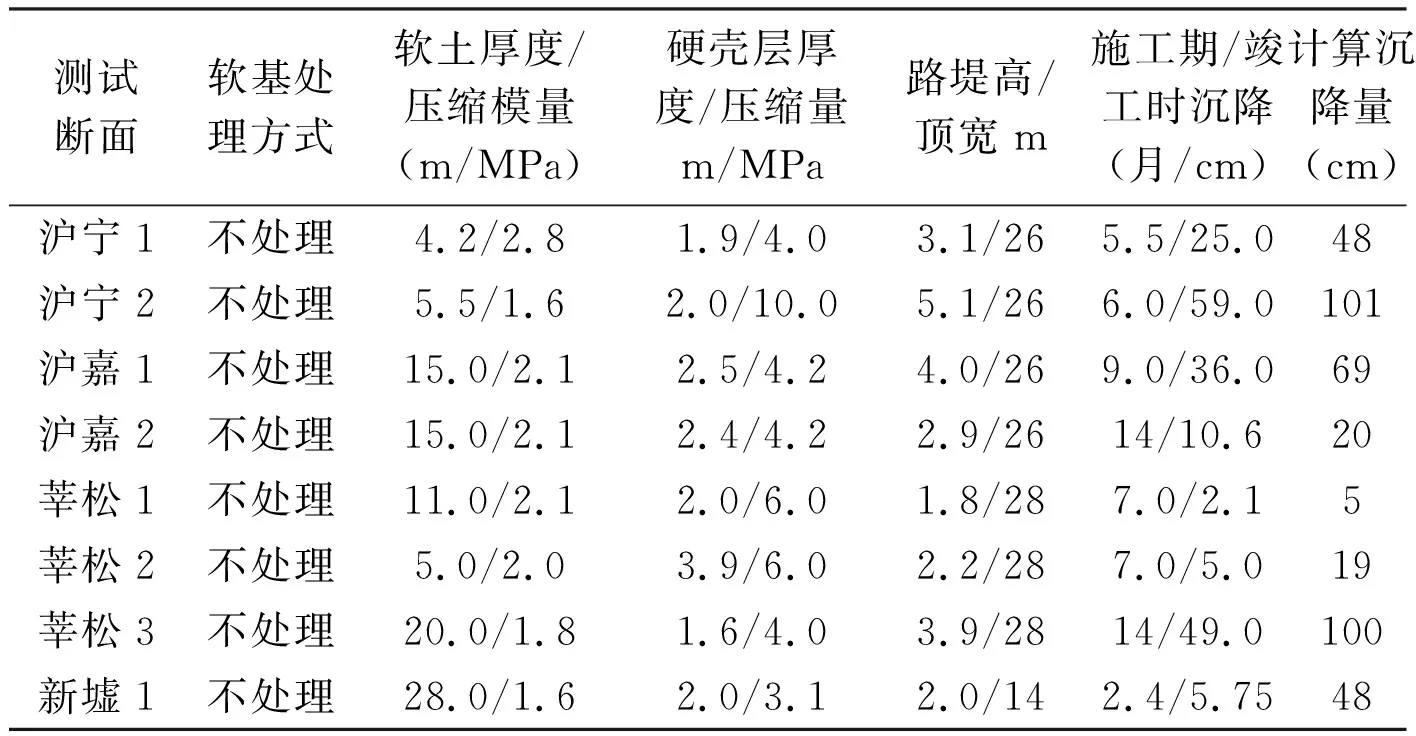
表1 软土硬壳层地区路基观测数据

研究者认为对软土硬壳层地基可以不进行处理的条件是：软土表层有1.5～3.0m的硬壳层，路堤高度为2.5m左右。研究人员将低路堤沉降较小的原因归结为：

(1)硬壳使得基底处的附加压力向下传播时，将应力扩散到下卧软土层上，称为应力扩散作用；

(2)硬壳层像板体一样覆盖在软土层上，当荷载作用于硬壳层并向下传递时，由于表层硬壳层的约束，限制了软土的自由位移，从而改变了软土地基中的应力分布，称为封闭作用。

沿海高速公路海丰段至沧州歧口位于河北省沧州市东部，为主要依托工程。为了明确路基下软土硬壳层地基中的位移变化规律，在该试验段选择断面进行了沉降监测,各断面的监测设备布置情况见图1。

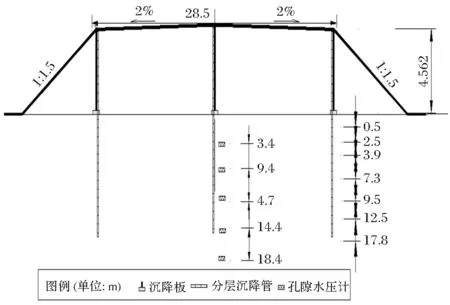
图1 设备布置平面图

2 地表硬壳层对地基沉降的影响

2.1 硬壳层地基竖向附加应力系数

路堤填筑在硬壳层上时，将出现应力扩散现象，竖向附加应力迅速减小，如图2中曲线3所示。图中曲线1表示均质地基情况，曲线2则表示上软下硬地基。应力扩散与土层厚度、泊松比、软土变形模量有关。

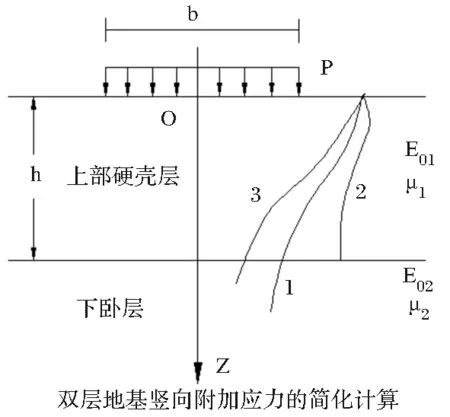
图2 地基应力分布

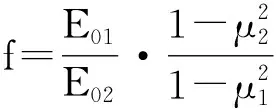
(1)

式中： E01—变形模量(硬壳层，kPa)；

E02—变形模量(软土地基，kPa)；

μ1—泊松比(硬壳层)；

μ2—泊松比(软土地基)。

叶果洛夫对条形荷载作用在软土硬壳层上时，硬壳层与软土分界面上的一点的附加应力求解方法：

σz=αEP0

(2)

式中：αE—软硬分界面上竖向附加应力系数。

叶果洛夫计算公式针对的是条形均布荷载的情况，只能计算出中心线与硬壳层底交点的应力。为了计算路堤荷载作用下任一点的附加应力，需要先将路堤梯形荷载转化为条形均布荷载，以便用叶果洛夫方法计算出中心线与硬壳层底面交点处的附加应力。

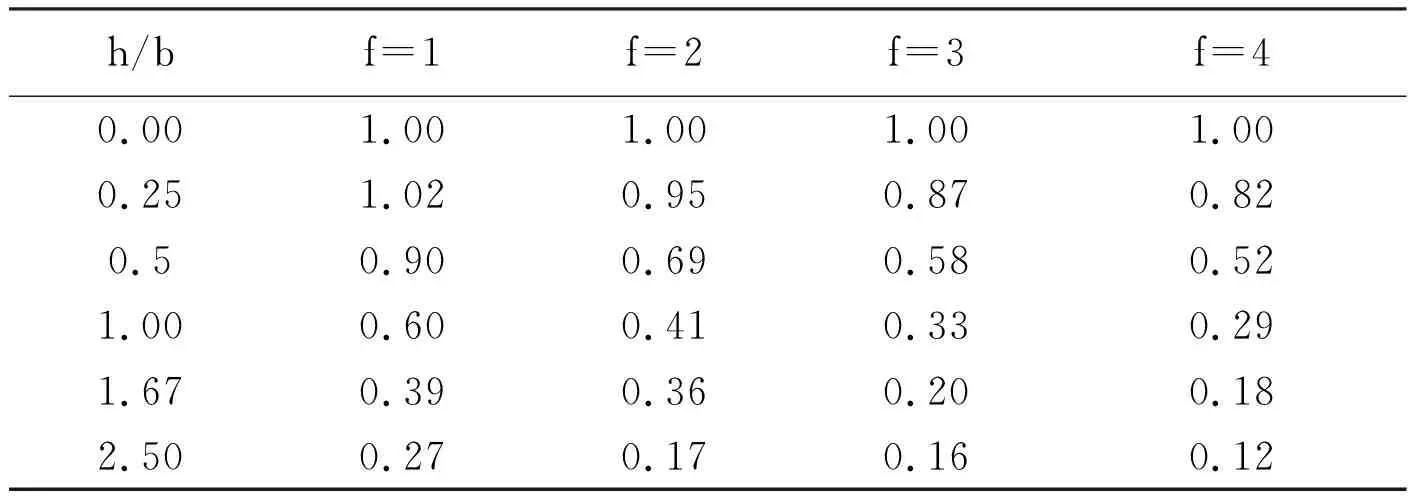
表2 竖向附加应力系数αE

2.2 梯形荷载等价宽度的确定

为了准确地计算出地基的沉降量，本节借助于ABAQUS有限元分析找到均布荷载与梯形荷载的等价关系。

图3 均布荷载有限元模型

两个模型唯一的区别是荷载形状，计算参数、加载方式完全一样，模拟分析时，保持某一个模型不变(梯形荷载)，通过调整矩形荷载的宽度使两种荷载下地基的附加应力基本一致，从而找到与梯形荷载对应的矩形荷载的宽度。

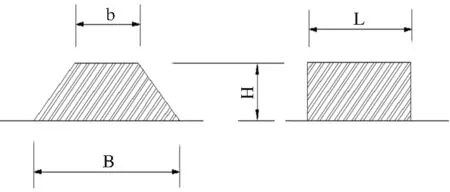
图5 等价模型

为了找到梯形荷载与条形均布荷载的等效宽度，对两种荷载进行模拟，计算分析可知：

ES1/ES2<3时，L=b+(B-b)/3

(3)

ES1/ES2>3时，L=b+(B-b)/4

(4)

式中：ES1—硬壳层压缩模量(kPa)；

ES2—软土层压缩模量(kPa)；

H—路堤高度(m)；

B—梯形荷载下底宽度(m)；

L—条形均布荷载宽度(m)；

b—梯形荷载上底宽度(m)。

3 路堤荷载作用下软土硬壳层地基沉降计算方法

(1)根据式(3)或式(4)将需要计算沉降的路堤荷载转化成条形均布荷载。

(2)根据式(1)计算上硬下软地基路堤中心线与软硬交界面交点的竖向附加应力。

(3)利用线弹性理论，计算硬壳层内竖向附加应力。

(4)等效深度确定：原理是将软土硬壳层地基转化为均质地基，使均质地基Z(图6)深度处M点的竖向附加应力与软土硬壳层地基M点的竖向附加应力相同。主要方法就是比较第二步与第三步的计算结果，找到等效深度。

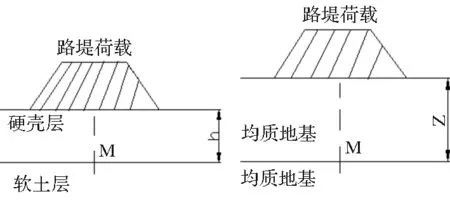
图6 等效深度确定

(5)求得Z值后，按照线弹性理论计算地基中各点的竖向附加应力系数，硬壳层中的应力则近似按照线性分布来计算。建筑规范中地基沉降公式如下：

S=ΦSS′=ΦS∑P0/ES1(Ziαi-Zi1αi1)

(5)

式中：s—基础总沉降，mm；

S′—地基沉降量(分层总和法)；

ΦS—变异系数；

n—计算深度内划分的土层数量；

ES1—第i层土的压缩模量(MPa)；

P0—附加压力(kPa)；

Zi—划分土层的厚度(m)；

αi—第i层土的附加应力系数。

4 现场监控结果与理论计算结果比较

沿海高速公路沧州试验段K42+400、K42+500、K42+600三个试验断面的路堤填土高度分别为5.5m、4.1m、3.4m。路堤顶宽28m，边坡坡度1∶1.5，填土容重18.5kN/m，对地基未作处理。

分别计算k42+400～k42+600的总沉降量，将最终计算结果列于表3：

表3 计算结果

从计算结果可以看出，分层总和法的计算结果远大于现场检测结果，修正后理论计算结果略大于现场检测结果，这说明修正的计算公式还是起到了一定作用。当不进行软基处理地段与软基加固地段想衔接时，需要考虑地基的不均匀沉降，这就需要考虑硬壳层的加筋作用以满足地基工后沉降的要求。

5 结论

(1)在软基处理路段与直接填筑路段，要注意沉降不均匀性，因为直接填筑路段软土固结较慢，因此必须要有足够的时间使直接填筑路段充分沉降。

(2)若不考虑硬壳层的应力扩散作用，设计中很可能会因为总沉降计算偏大导致计算出的工后沉降过大而达不到设计要求，因此有必要对传统的地基沉降计算方法进行改进，提出了修正后的软土硬壳层地基沉降计算方法。