初中数学教学中如何训练学生的发散性思维

摘 要：发散性思维培养是初中数学教学的重要目标，其不仅有助于积极、活跃的课堂环境营造，还对教学效果及学生学习能力提升具有重大影响。文章在阐述初中数学教学发散思维培养必要性的基础上，就发散思维培养中的制约因素进行分析，并系统性地指出发散思维的培养策略，以期有利于学生发散思维的培养，进而在提升教学水平的同时，实现学生的全面发展。

关键词：发散性思维;初中数学;思维创新

中图分类号：G633.6      文章编号：2095-624X（2019）18-0116-02

一、初中数学教学发散性思维培养的必要性

其一，初中数学教学中，发散性思维的培养使得学生能够从多个角度思考问题，从教学实施过程来看，发散性思维的应用使得学生在课堂上的表现更加活跃，其在刺激学生思维能力的同时，实现了有意学习与无意学习的高度耦合，对良好教学氛围的营造具有重大影响。其二，发散性思维的培养、应用使得学生对数学知识的掌控更加全面。具体而言，学生思维的发散以现有知识为基础，其在新问题解决的基础上，实现了已掌握知识的有效调动，从而在多角度、多方式思考问题的基础上，实现了基础知识的系统性和连贯性掌握。其三，现代教学理念下，人们对数学教学实践提出了较高的培养目标，教学实践中必须注重学生“数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析”的六大核心素养培养[1]。从实践效果来看，发散性思维是对学生思维能力创新的具体实践，其对学生数学核心素养培养和全面发展具有重大影响。由此可见，教学实践中，进行发散性思维的培养势在必行。

二、发散性思维培养的制约因素

其一，步入初中以来，数学知识内容更加丰富，概念性更强，大量理论化、抽象化的知识理解使得学生学习难度明显增加，与其他学习科目相比，其趣味性明显降低，由此降低了学生的学习兴趣，制约了数学发散性思维能力的培养。其二，善于思维创新、乐于问题探索是发散性思维培养的最初动力。然而在实践中，部分学生还处于被动接受知识的状态，其不能积极主动地进行问题思考和解决，这是制约学生数学发散性思维培养的根本原因。其三，已掌握知识是学生进行思维发散与创新的基础，数学教学中，模块化是基础知识学习的重要特征，要实现学生思维发散能力的有效培养，其还应注重知识模块的耦合，实现抽象化概念知识的具象表达。其四，注重思维广阔性与联想性的把控是初中数学教学发散思维培养的关键。实践过程中，学生要从多个层面、多个角度进行问题的解答，实现一题多解，然而从实践过程来看，学生在一题多解把控中尚显不足。新时期，要实现学生发散性思维的高效培养，实现学生学习能力的提升，教学实践中，教师就必须注重这些问题的系统解决。

三、初中数学教学中发散性思维的培养策略

层次性是发散性思维培养的重要特征。就初中数学教学实践而言，“思维广阔、富于想象、擅于分解结合和引申推理、敢于创新”是初中数学教学中学生发散性思维培养的集中表现[2]。具体而言，其培养策略表现如下。

1.注重数学趣味训练

“有趣的材料容易记、记得牢”是人们记忆心理的重要特征。对于初中数学教学而言，数学教师就应在教学实践中贯彻趣味性理念，实现教学过程、发散思维培养的趣味化。设置一些找规律类的题目是数学趣味性训练的有效手段。譬如，在题目13+23+…+103计算过程中，教师也引导学生进行13+23=9，（1+2）2=9;13+23+33=36，（1+2+3）2=36等式的计算，使学生发现13+23+…+n3=（1+2+…+n）2这一规律，从而在增强数学趣味性、实现问题解决的同时，实现学生发散思维的有效培养。

2.实现数学设问引导

发散性思维是从不同方向考虑解决问题的多种可能性的思维过程。数学教学实践中，要实现多元性思维的有效培养，教师就应注重数学设问的有效引导，在学生富于想象的基础上，实现多种问题解决途径的思考，促进学生发散思维培养。数学公式是学生进行数学问题解答的重要依据，在教学实践中，教师就应以公式为基础，对学生进行公式转化、问题解决的有效引导。譬如，教师可引导学生对一元二次方程ax2+bx+c=0（a≠0）进行根式转化，从而确保根式x1，2=—的获得。然后在问题（x-4）2=0;x2+4=0等问题解答的同时，对一元二次方程的解法进行探索;并帮助学生推导罗列各种算法的正确性。通过各种问题的引导，学生可以试下基础知识的高效理解和准确记忆，从而在问题引申、推进习惯养成的基础上，实现发散思维的培养和认知水平的提升。

3.发挥数形结合作用

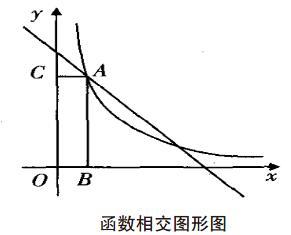
初中數学学习中，数学概念的抽象性对学生的学习造成了较大困扰，其在影响学生学习兴趣的同时，制约了他们发散性思维的培养。基于此，在教学实践中，教师应注重数形结合方法的合理应用，在数形结合的基础上，实现抽象数学问题的具象化表达，从而省却烦琐的计算过程，实现问题解答过程简化、问题思维模式的拓展。譬如，一次函数y=-x+3与反比例函数y=—相交于坐标轴第一象限，且相交点为A，若依据条件“AB垂直X轴”和“AC垂直Y轴”进行矩形ABOC的面积和周长求取，则教师也引导学生进行两者相交图形的构建（如下图）然后在图形的具象指引下，实现矩形ABOC面积=AC×AB = xy=2;矩形ABOC周长=2（AC+AB ）=6的有效计算。

4.注重一题多解应用

发散性思维的培养要求学生具备灵活的思维，实现解题过程的创新。教学实践中，要确保学生思维创新能力得到有效训练，实现发散性思维培养，教师就应注重一题多解策略的有效应用。具体而言，针对较为典型的数学题目，教师可引导学生从多个角度进行思考，譬如，在三角函数解答过程中融入方程理念、数形结合理念等，实现课本知识的有效延伸，并在问题解答过程中，实现思维过程的有效拓展。

四、结语

发散性思维培养对初中数学教学实践开展具有重大影响。教学实践中，教育工作人员只有充分认识到发散性思维培养的必要性，并在分析数学问题的基础上，进行发散性思维培养策略的高效应用，才能确保学生发散性思维的有效培养，进而在提升教学水平的同时，实现学生的全面发展。

参考文献：

[1]朱丽芳.初中数学教学中学生发散性思维培养探析[J].中学教学参考，2017（2）：34-35.

[2]胡会.试析初中数学教学中学生数学思维能力的培养[J].决策与信息（下旬刊），2016（12）：161.

作者简介：刘妍（1978—），女，湖南衡阳人，中学一级教师，硕士。