数学教学，以核心素养为纲

龙立芬

《中学数学教学参考》2018年中旬刊1-2期，刊发了裴亚光老师就“第四届初中数学名师创新型课堂研修会”的点评稿《课堂创新：以数学的核心素养为纲》.裴老师对教学案例的分析鞭辟入里，对教学实践的指导高瞻远瞩，读裴老师的文章，获得的不仅是教学技能的提升，教学智慧的丰富，更多的是教学思想的引领，教学热情的激发，顿有醍醐灌顶之感，教学视野倍加开阔，心情随之豁然开朗.本文就自己执教的人教版“19.1.1变量与函数”，谈谈自己的学习心得.

一、教学内容分析

函数是重要的数学概念，它有广泛的应用，在义务教育阶段的数学课程中占有重要地位，学生初中数学认识的第一次飞跃是代数式的学习，由具体的数到具有普遍意义的式.第二次飞跃是函数的学习，由静止不变的数到运动变化的数.本节课是学生学习函数的入门课，目标任务是准确认识变量与常量的特征，初步感受现实世界各种变量之间互相联系的復杂性，同时感受到数学研究方法的化繁为简，知道在初中阶段主要研究两个变量之间的特殊对应关系.之前教材是把变量与函数分成两节课安排的，2016年春季教材将变量与函数合并成一节课内容，素材也略有调整，很显然教材的这个调整更加科学合理.现行教材首先通过4个含有变量之间单值对应关系的问题，引出常量与变量的概念，也为随后引出变量之间单值对应关系进而学习函数的定义做好铺垫.接着，从具体到抽象，认识变量之间单值对应关系，即当一个变量取定一个值时，另一个变量有唯一确定的值与之对应，从而揭示函数、函数值的概念.函数的一般概念，即变化与对应意义下的函数定义是本课的重点，也是难点.最后，通过一个例题和两个练习巩固对函数、函数值概念的理解，引发自变量取值范围的思考.

二、教学过程及注意事项

（一）我自学，我明白

1.自学教材P71内容，思考下列问题：

（1）汽车以60千米/时的速度匀速行驶，行驶里程为s km，行驶时间为t h，填写下表，s的值随着t的值的变化而变化吗？

（2）每张电影票的售价为10元，如果早场售出票150张，午场售出205张，晚场售出310张，三场电影票的票房收入各多少元？若设一场电影售出票x张，票房收入为y元，y的值随着x的值的变化而变化吗？

（3）圆的半径r分别为10 cm，20 cm，30 cm时，圆的面积S分别是多少？S的值随着r的值的变化而变化吗？

（4）用10米长的绳子围一个矩形.当矩形的一边长x分别为3 cm，3.5 cm，4 cm，4.5 cm时，它的邻边长y分别是多少？y的值随着x的值的变化而变化吗？

2.什么是变量？什么是常量？

3.试列举生活中变量与常量的实例.

【注意事项】围绕学生比较熟悉的例子（2个生活问题、2个几何问题），有助于学习兴趣的激发.常量是不发生变化的量，变量是变化的量，都是针对某个变化过程而言的.本节不宜过早提及常量可做特殊的变量的情况，以免造成常量和变量的混淆.

（二）我思考，我辨析

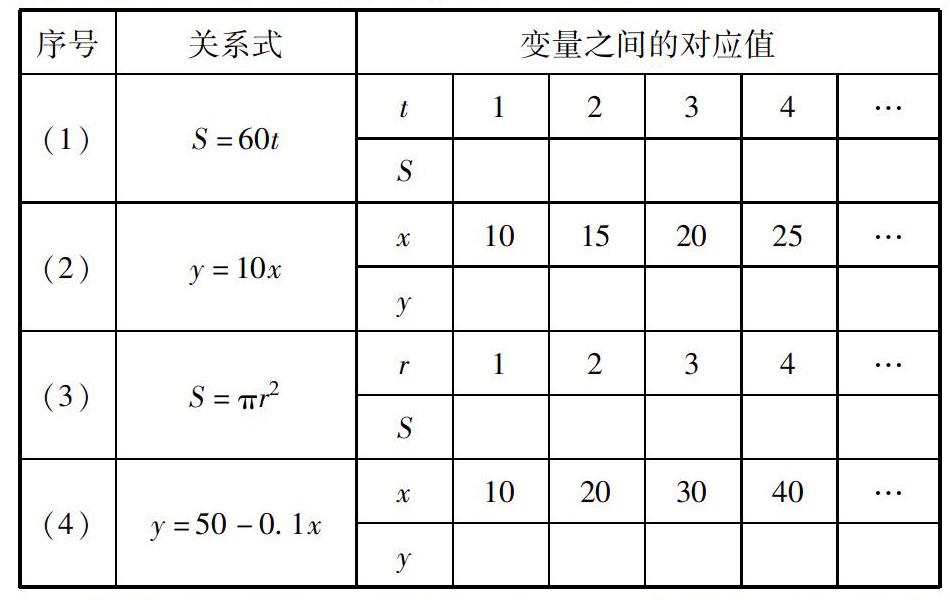
1.试用数学式子表示上述（1）-（4）变化过程中变量和常量间的关系.

2.思考：（1）-（4）中是否各有两个变量？（是）同一个问题中的变量之间有什么联系？填表说明.

序号关系式变量之间的对应值

归纳：上面每个问题中有两个变量，当其中一个变量取定一个值时，另一个变量就有唯一确定的值与其对应.

3.下面问题中的两个变量之间还有上述关系吗？

（5）李明的数学单元测验成绩m与单元数n之间的关系.

（6）北京市某日8时到次日5时，气温T/℃与时间t/时之间的关系.

【注意事项】教材是通过学生探索实际问题中存在的大量的变量之间关系，抽象出函数的概念的，它让学生在分析问题的过程中，感受两个变量之间存在一定的关系，它们的表示方式是多样的，如可以通过列表的方法表示，可以通过画图像的方法表示，还可以通过列解析式的方法表示，但都有着共性：其中一个变量依赖于另一个变量，从而使学生能更好地理解函数的概念，为后面学习各种函数打好基础.这样的素材很多，教学中尽可能选择学生身边的实例，更有利于调动学生的思维参与和情感参与.

（三）我归纳，我增长

如上述问题，在一个变化过程中，如果有两个变量x与y，并且对x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.如果当x=a时，y=b，那么b叫作自变量x=a时的函数值.

【注意事项】引例（3）和（5）中y对x是单值对应，因此，y是x的函数;但x对y不是单值对应，因此，x不是y的函数.本节教学问题暗示了哪个变量是自变量，不需要着重讨论两个变量是否都可以作为自变量的问题，根据学生在课堂的表现而定.函数概念的表述比较抽象，学生往往不能一下子从其定义理解其内涵，教学中注意由具体例子逐步过渡到抽象定义，有了定义后，还需要适当用具体例子对定义中的文字加以解释.另外，函数与函数值学生也易混淆，需要适当结合实例引导学生认识到一个函数可能有多个不同的函数值，函数是变量，函数值是常量，结合函数定义，进一步认识y唯一确定，但x不一定唯一.

（四）我练习，我提高

1.指出上述（1）—（6）问题中，谁是自变量？谁是自变量的函数？自变量可以任意取值吗？它们的取值范围分别是什么？

2.判断下面两个变量之间是否是函数关系？

【注意事项】练习是思考探究的自然延续，环环相扣的问题设置，让课堂教学递进攀升、相互融合，实现“有意而为，无意而成”的意境，达到“真水无香，教育无痕”的效果.练习1中自变量的取值范围，不仅要考虑函数关系式有意义，而且要使实际问题有意义，教学中不做过多过深的延伸.学生对练习2并不陌生，特别是小学阶段，这样暗含程序性运算的例子很多，却不曾关注过其中隐藏的函数关系，这个问题可以引导学生注意函数存在于许多数学问题之中，以函数的观点可以重新认识已学过的数学内容.练习3的难度提升了一个层次，再次将问题聚焦到“y是否是对x的单值对应？”，加强函数定义的理解，作为机动练习根据学生的学习情况而定.

（五）我小结，我收获

1.学生小结：通过本节课的学习，你有什么收获？（学生畅谈）

2.教师小结：

（1）知识总结：

函数概念的要素：

① 两个变量x与y;

② x的值确定后，y有唯一确定的值与其对应.

函数值的概念：如果当x=a时，y=b，那么b叫作自变量x=a时的函数值.

x=a時，y=b（b是唯一的）;y=b时，x=a（a可能不唯一）.

函数的表达形式：数学式子、列表格、画图形.

（2）学法指导：

【注意事项】课堂小结并不是知识的简单重复和罗列，小结须立足“四基”，强调知识技能的同时，积累思想方法和活动经验.学生的小结往往具有“漫谈”的色彩，需要教师引导梳理，重难点问题着重强调，让学生更加明晰本节知识脉络，感受到自己的进步，激励学生不断进步.

（六）我作业，我发展

必做题：1.列举几个身边函数的实例;

2.习题19.1复习巩固1、2题.

选做题：习题19.1综合运用10、11题.

【注意事项】尊重学生的个体差异，为不同学生的发展创造条件，作业分层推荐，以满足不同层次学生的需求.及时搜集掌握学生的学习效果，及时回授评定，以便有针对性地组织质疑和讲解，帮助学生克服思维障碍，补救知识或方法方面的漏洞.

（七）板书设计

【注意事项】板书力求内容精当，线索清晰，布局合理，书写工整，体现数学学科的特征.

三、教学感悟与思考

函数教学是中学数学的一条主线，变量与函数的教学就是这条主线的转折点.本节课的核心知识是函数的概念，它融数学抽象、建模思想、逻辑想象为一体，承载着发展学生核心素养和数学核心素养的重要作用，学生学习函数之旅也是发展学生数学抽象、逻辑推理、数学建模、数学运算、直观想象的必经之路.函数概念很抽象，因此，教学中不可一蹴而就.突破重难点的策略是突出“变化”和“对应”的思想.从概念的起源来看，函数是随着数学研究事物的运动、变化而出现的，它刻画了客观世界事物间的动态变化和相互依存的关系，这种关系反映了运动变化过程中的两个变量之间的制约关系.因此，变化是函数概念产生的源头，是制约概念学习的关键点，同时也是概念教学的一个重要突破口.通过大量的、典型的生活实例，让学生反复观察、反复比较、反复分析每个具体问题的量与量之间的变化关系，把静止的表达式看成动态的变化过程，让他们从原来的常量、代数式、方程式和算式的静态的关系中，逐步过渡到变量、函数这些表示量与量之间的动态的关系上，使学生初步感知“大千世界，万物皆变”，函数就是研究这种变化的数学模型.今后，学生通过进一步对“函数的图像”“一次函数”“二次函数”“反比例函数”的学习，对函数概念的认知也会随之呈现螺旋式上升.

总之，数学教学活动是学科核心素养培养的主要途径，知识不是目的，能力也不是全部目的，学生素养提升才是最终目的.在众多素养中，只有抓住了核心素养，才可能实现教学的全部目的.