基于小波神经网络的污水厂总磷预测模型
郭宗敏 徐冰峰 山丕斌

摘 要:污水厂进水污染物与出水总磷的变化规律呈高度非线性,而传统机理预测模型需要依据经验设定大量参数,预测精度较低,预测相对误差处于15%~25%之间。为提高预测精度,以进水化学需氧量、总氮、氨氮、总磷、进水量5个进水指标与出水总磷浓度的映射关系建立小波神经网络预测模型。结果表明,小波神经网络模型模拟相对误差为9.87%,相较于机理模型,预测误差降低了5%~15%;同时模型收敛速度快,具有强大的非线性拟合能力,运行稳定性強,对污水厂实际运行中出水总磷预测有一定参考作用。
关键词:进水污染物;总磷出水浓度;小波神经网络
DOI:10. 11907/rjdk. 191715 开放科学(资源服务)标识码(OSID):
中图分类号:TP302文献标识码:A 文章编号:1672-7800(2019)009-0038-04
Research of TP Prediction Model in Wastewater Treatment Plant
Based on Wavelet Neural Network
GUO Zong-min,XU Bing-feng,SHAN Pi-bin,ZHOU Ya-lin
(Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China)
Abstract: The variation of influent pollutants and effluent TP in wastewater treatment plant is highly non-linear. The traditional mechanism prediction model needs to set a large number of parameters based on experience, so that its prediction accuracy is low,the predicted relative error is between 15%-25%. In order to solve this problem,this paper establishes a wavelet neural network prediction model based on the mapping relationship between COD, TN, NH3-N, TP, influent volume and effluent TP. The results show that the relative error of the wavelet neural network model simulation is 9.87%, and the prediction error is reduced by 5%-15% compared with the mechanism model. In summary,the wavelet neural network model has fast convergence speed, strong non-linear fitting ability, strong operational stability, and higher prediction accuracy than the mechanism model, which can provide reference for predicting effluent TP in actual operation of wastewater treatment plant.
Key Words: influent pollutants;effluent TP concentration;wavelet neural network
0 引言
影响污水厂除磷效果的因素较多,而污水厂进水水质中的化学需氧量(COD)、总氮(TN)、氨氮(NH3-N)、总磷(TP)等污染物含量均与TP去除效果有关,因此污水厂进水水质在很大程度上与出水TP浓度相关[1-2]。由于污水厂在实际运行中进行出水TP浓度预测较为困难,所以通过运用数学模型进行模拟,分析和掌握污水厂进水水质与TP出水浓度的规律,对于提高污水厂除磷效果具有重要现实意义。
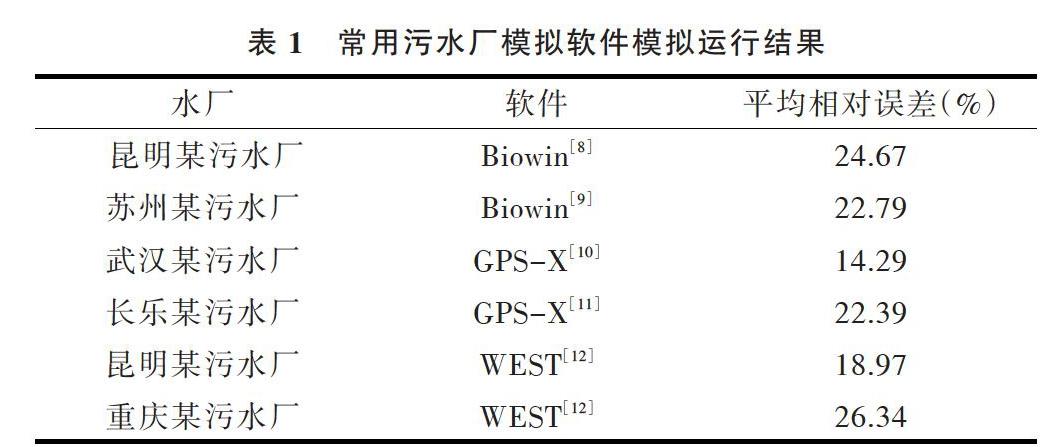
目前国内外污水厂除磷模拟数学模型主要采用机理模型,应用较多的主要有Biowin[3-4]、GPS-X[5-6]、WEST[7]等软件。李帅帅[8]、杭晨等[9]利用Biowin软件建立了污水厂除磷机理模型,周国强[10]、陈钰林[11]利用GPS-X软件建立了污水厂除磷机理模型,张蓉[12]利用WEST软件建立了污水厂除磷机理模型。如表1所示,机理模型模拟相对误差在10%~25%之间。
由于污水厂生物除磷过程涉及的机理过于复杂和不确定,使得机理模型参数过多,且很多参数都是凭借经验或根据预设值设定的,使其在实际污水厂除磷运行中的模拟精度不高,从而降低了机理模型在污水厂除磷中的应用价值。人工神经网络具有良好的非线性处理能力,针对机理模型在污水厂除磷预测中的局限性,本文利用小波神经网络模型这一非机理模型,实现对出水TP浓度的动态预测,克服机理模型构建复杂的缺点,可提高模型预测精度,为污水厂提高除磷效率提供参考。
1 小波神经网络
1.1 小波神经网络概述
小波神经网络是将BP神经网络隐含层传递函数用小波函数替换的一种优化神经网络,采用有监督学习的模式,通过误差反向传递的最速下降法逐步修改权值达到训练目的。小波神经网络能较好地解决非线性、高维数等实际问题,具有良好的泛化能力,在众多非线性模拟预测领域有很好的应用价值[13-15]。
1.2 小波神经网络构建
1.2.1 影响因子确定
污水厂出水TP浓度与进水水质中各组分存在高度非线性关系。研究表明进水指标中影响微生物去除总氮的因素主要有进水COD、TN、NH3-N、TP、进水量等[16-17],因此本文选取这5个进水指标作为影响因子。
1.2.2 小波神经网络结构
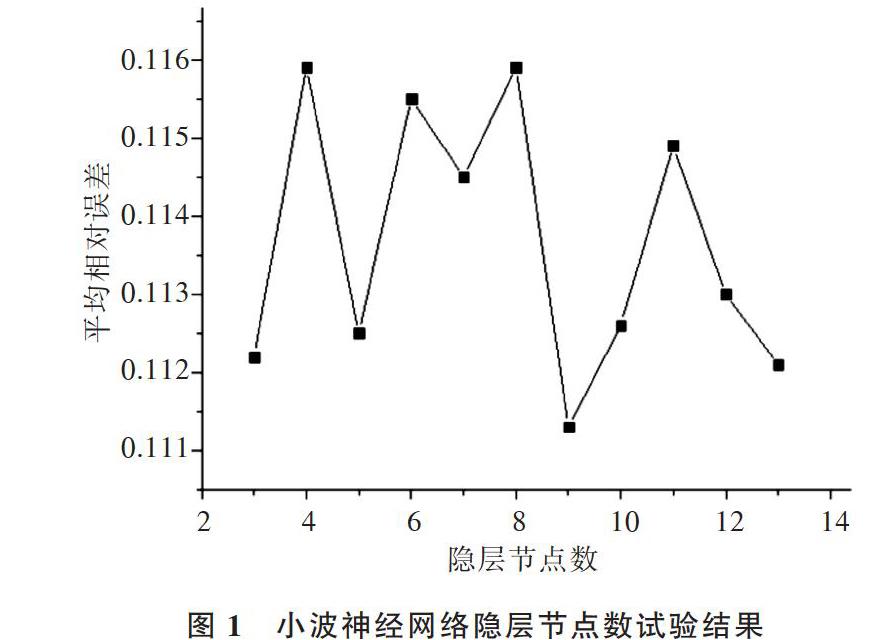
小波神经网络通常包括输入层I、隐含层J、输出层K。本文将5个进水指标作为5个输入层节点,出水TP浓度作为输出层节点。目前并没有一个理想的解析式确定合理的隐层节点数,通常根据经验在[log2m,log2m+10]范围内选取(m为输入节点数)[18]。本文面向隐层节点数从3到13时的网络测试误差进行试验,如图1可见,试验结果表明测试最小误差发生在隐含层节点数为9时,因此本研究选取隐层节点数为9。综上所述,本模型采用5-9-1的3层网络结构。
1.2.3 小波神经网络训练
(1)数据处理。在小波神经网络训练前,需对数据进行处理。本文数据来源于云南省滇南某CASS工艺污水厂2017年1月至6月进出水指标数据,共169组。根据已有研究发现,通常将数据样本中的70%~90%作为训练样本,10%~30%作为测试样本较为合适[19-21],可保证BP神经网络有足够的训练样本。本文将169组数据分为3组分别进行检验,每组训练样本和测试样本数分别分为159/10、149/20、139/30,结果显示3种分组方案结果相似。综上所述,本文最終以149/20的分组方案对模型模拟预测效果进行检测。由于各指标数量级不同,需要对数据进行归一化处理,使所有数据在[-1,1]范围内。
(2)正向传播过程。正向传播的目的是将149组训练输入数据中,将5项进水指标数据批量加权计算至各隐含层,各隐含层通过传递函数将数据映射到[-1,1]区间后,再通过加权计算输出为出水TP浓度,其过程如图2所示。
首先计算隐含层输入,将149组训练数据中每一组的5个影响因子分别作为含149个元素的行向量X1、X2、X3、X4、X5,构建5×149的输入矩阵X=[X1,X2,X3,X4,X5]T。将9个隐含层与5个输入层之间的连接权值ω1依次排列构建权值矩阵W1,其中第j行第i列元素ωji表示第i个输入节点与第j个隐含层节点的连接权值。连接权值ω的初始值一般是随机给定,通常将初始权值设定为较小的非零随机值。因此本文初始权值亦采用经验值随机选取,经验值为(-2.4/F,2.4/F)之间,其中F为输入层节点数。在Matlab中利用矩阵进行计算,得到9×149的隐含层输入矩阵U,其中第j行第n列元素标志第n组输入数据在第j个隐层节点的输入值:
Ω值影响小波函数正弦波的频率和波峰,本文在[0,3]范围内选取多组Ω值进行试验,发现在[1.25,2.25]范围内正弦波波峰处于[1,2]内。考虑到隐含层经过加权到输出层后所有输出数据分散保持在[-1,1]内,运算小波函数输出应留有一定余量,本文在[1.25,2.25]范围内选取了3个不同值Ω进行试验,如图3可知,Ω参数选择1.75。
此外,小波函数应加入平移伸缩参数ah和平移参数bh。ah影响小波函数宽度,本文在[0,3]范围内选取了多组ah值进行试验,发现ah在[0.5,1.5]范围内完整正弦波在[-2,2]内,因此本文在[0.5,1.5]范围内选取3个ah值进行试验,如图4所见,为使[-1,1]范围内尽量包含完整正弦波,ah选择0.5为宜。bh影响小波函数的位置,而由于输入数据在[-1,1]内对称,无需平移,故本文bh取0。
将输出层与9个隐含层之间的连接权值ω2依次排列构建1×9权值矩阵W2,其中第j个元素wj表示第j个隐含层和输出层之间的连接权值。在Matlab中利用矩阵计算得到1×149的输出矩阵Y,其中第n个元素表示第n组数据的网络输出值。
(3)反向误差传递过程。其目的是运用梯度下降法根据网络输出值和期望输出值之间的误差不断调整各节点权值,从而不断减小误差,直到权值能准确反映5项进水指标与出水TP浓度的映射关系,其过程如图5所示。
其中,η为学习率。η控制小波神经网络误差反向传播调整权值时的调节力度,是保证网络能够收敛且收敛速度较快的关键。若学习率太小,则使网络收敛过慢,增加网络训练次数,从而降低网络建立的速度;若学习率太大,则造成权值调整量过大,使训练不收敛。本文选取[0.000 1,0.1]范围内的10个η值进行试验,发现η=0.003时网络收敛且收敛速度最快,最终确定网络学习率η=0.003。
若Error仍在减小,则再次迭代计算反向误差传递过程和正向传播过程,直到Error减小量很小或不再改变时停止迭代,此时网络收敛,训练完成。小波神经网络训练流程如图6所示。
2 网络测试与结果分析
利用20组测试数据分别对传统BP神经网络和小波神经网络进行测试,对比分析两种网络的收敛速度和模拟精度。
2.1 收敛速度
由图7、图8可知,BP神经网络前300次迭代Error减小幅度较大,在300次迭代后Error趋于平稳,网络收敛,而小波神经网络迭代100次后网络就已收敛,可见对BP神经网络进行优化的小波神经网络收敛速度明显快于优化前的BP神经网络。
2.2 模拟精度
结果如图9和表2所示,相较于BP神经网络,小波神经网络对于出水TP浓度预测平均相对误差降低了2.44%,决定系数提高了0.052 7,均方根误差降低了0.004 8,可见,小波神经网络相较于BP神经网络模拟精度更高。
3 结语
本文利用小波神经网络综合多个进水水质因素预测出水TP浓度。利用机理模型软件进行建模预测精度较低,平均相对误差在10%~25%之间,而利用优化BP神经网络得到的小波神经网络建立的非机理模型收敛速度快,且平均相对误差为9.87%。对比分析发现,相较于机理模型,非机理模型能够明显提高预测精度。结果表明该小波神经网络模型具有良好的模拟性能,可为模拟污水厂预测出水TP浓度提供有效参考。

