施工期48 h内锚下有效预应力时间及温度效应修正

樊见维，胡光明，高华睿，常晓娟

(1.陕西高速公路工程咨询有限公司，陕西 西安 710061； 2.山东大学 岩土与结构工程研究中心，山东 济南 250061)

0 引 言

随着中国公路桥梁建设的快速发展，预应力混凝土桥梁结构因其在经济性、耐久性、安全性等方面的优势，在桥梁施工领域中得以大量应用。但是，已有研究表明预应力混凝土梁桥会随其服役时间的增长而产生一系列的病害及下挠问题[1-2]。预应力张拉质量是影响预应力混凝土梁服役性能的关键因素，而外界环境以及材料自身特性的共同作用容易导致预应力混凝土梁桥有效预应力不断衰减[3-4]。

由于在桥梁施工期内存在施工误差等不确定性因素，以及在运营服役期内混凝土材料的劣化、汽车荷载的反复作用、超载造成混凝土的开裂及下挠等，会使有效预应力计算值与实际值之间存在较大偏差，影响到桥梁结构的使用性能和使用年限，严重时还会导致桥梁垮塌。Roller[5]研究得到1年半的预应力损失为11.4%；Chouman[6-7]研究得到后张法预应力混凝土梁1年的预应力损失为4.04%～20.32%；Barr[8]研究得到3年的预应力损失为27.5%；Natio等[9-10]研究得到三跨预应力混凝土连续梁桥12年的预应力损失为32.7%。根据已有研究可以看出，预应力损失变化量差异较大。

本文依托现场试验得到20 m预应力混凝土箱梁钢绞线48 h内锚下有效预应力的变化测试值，通过有限元模拟施工阶段预应力混凝土梁有效预应力损失变化的规律，通过对比分析确认实测数据和理论计算值的有效性，进行锚下预应力时间效应及温度效应修正。

1 锚下有效预应力时间松弛效应和温度效应测试方案

1.1 测试梁

选取陕西省某高海拔地区在建高速公路预制梁场中20 m预制箱梁6片，其截面尺寸相同，其中箱梁的预应力束形式有2种类型，A类和B类。预制主梁混凝土采用C50混凝土，钢绞线直径为15.2 mm，抗拉强度标准值为1 860 MPa，张拉控制应力为1 395 MPa。预制混凝土梁抗压强度达到设计混凝土强度等级的90%后张拉预应力钢束。箱梁张拉顺序为N1、N2、N3，具体梁体规格见表1及图1。

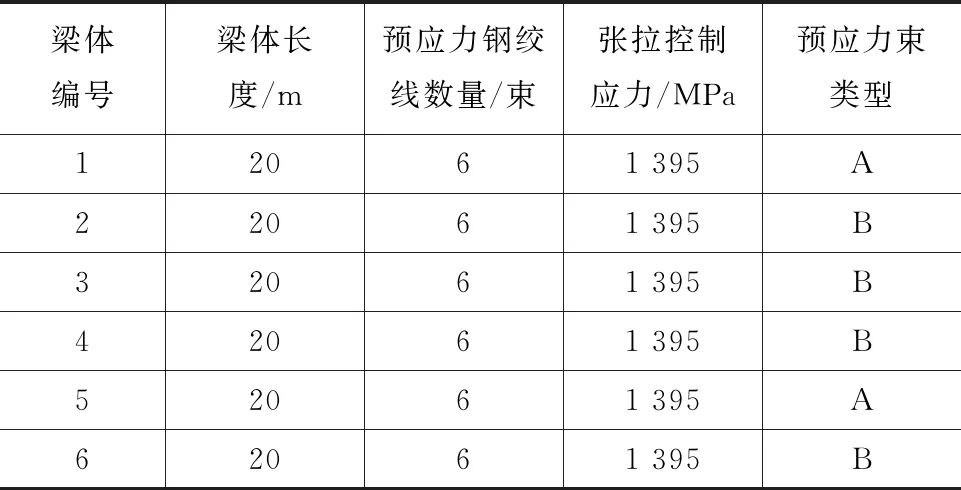
表1 梁体规格

注：A类预应力钢绞线N1、N2、N3均为4根；B类预应力钢绞线为N1、N2各5根，N3为4根。

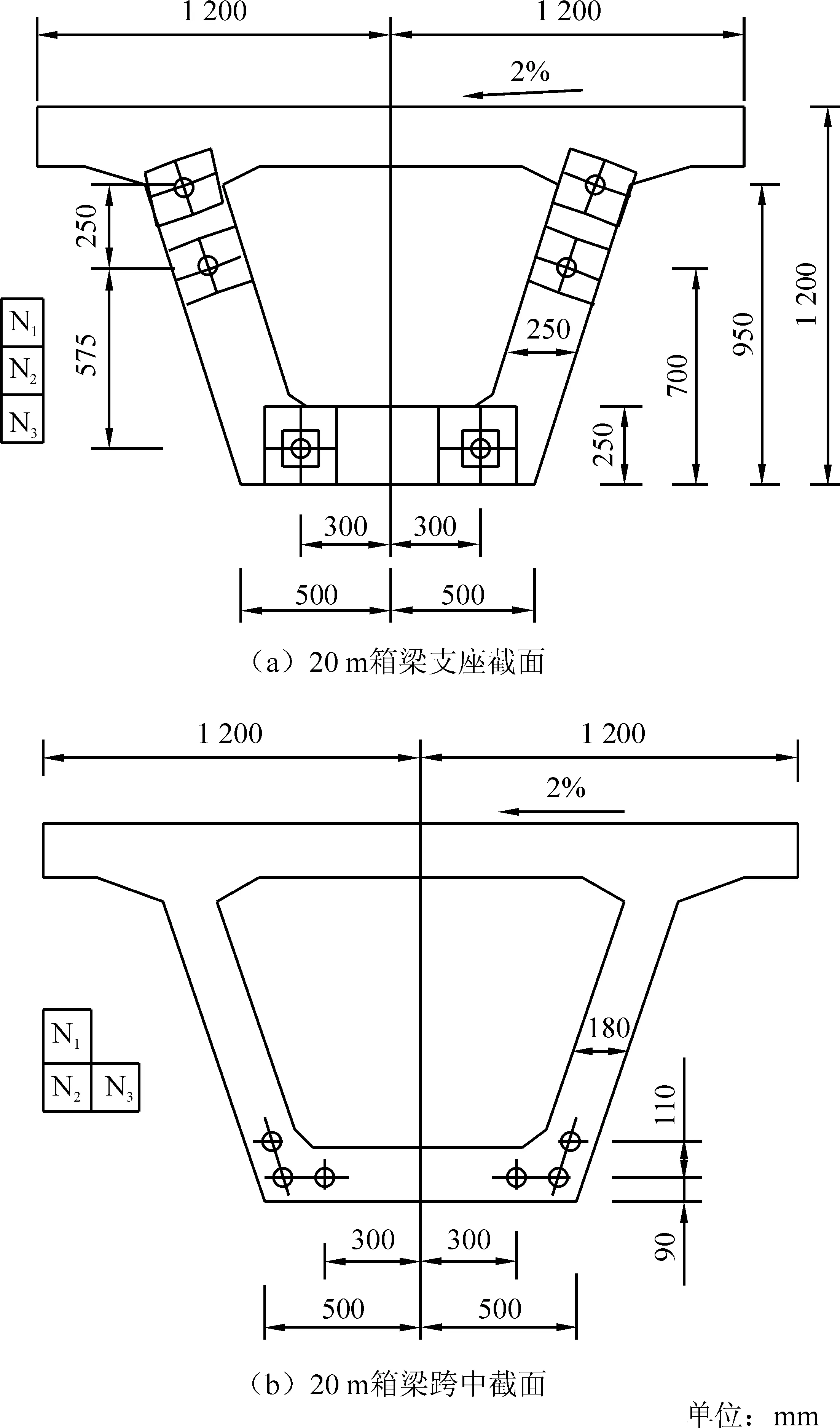
图1 试验梁截面形式

1.2 试验设备

自动化综合测试系统是一种功能强大的分布式全自动静态网络数据采集系统，由上位机、采集模块(MCU)、系统软件及相关配件组成[11-12]。采集模块(MCU)是本系统的二次仪表，由穿心式压力传感器、温度传感器及相关配件组成。现场测试设备如图2所示。

图2 现场试验设备

1.3 测试过程

在梁体混凝土浇筑并养生7～8 d后，进入预应力钢束的张拉施工阶段。在预应力钢束未张拉前，将压力传感器安装至锚具与梁端之间(仅在梁体单侧放置)，进入张拉阶段；在张拉过程中，每分钟采集一次锚下预应力数值和环境温度数值，实时监控锚下预应力变化过程。待张拉结束3 h后，将设备调成自动采集模式，采样频率为每10 min一次。试验过程如图3所示。

图3 现场试验过程

2 锚下有效预应力测试结果及时间修正

2.1 测试结果

48 h内各束钢绞线有效预应力随时间及温度的变化曲线如图4所示。

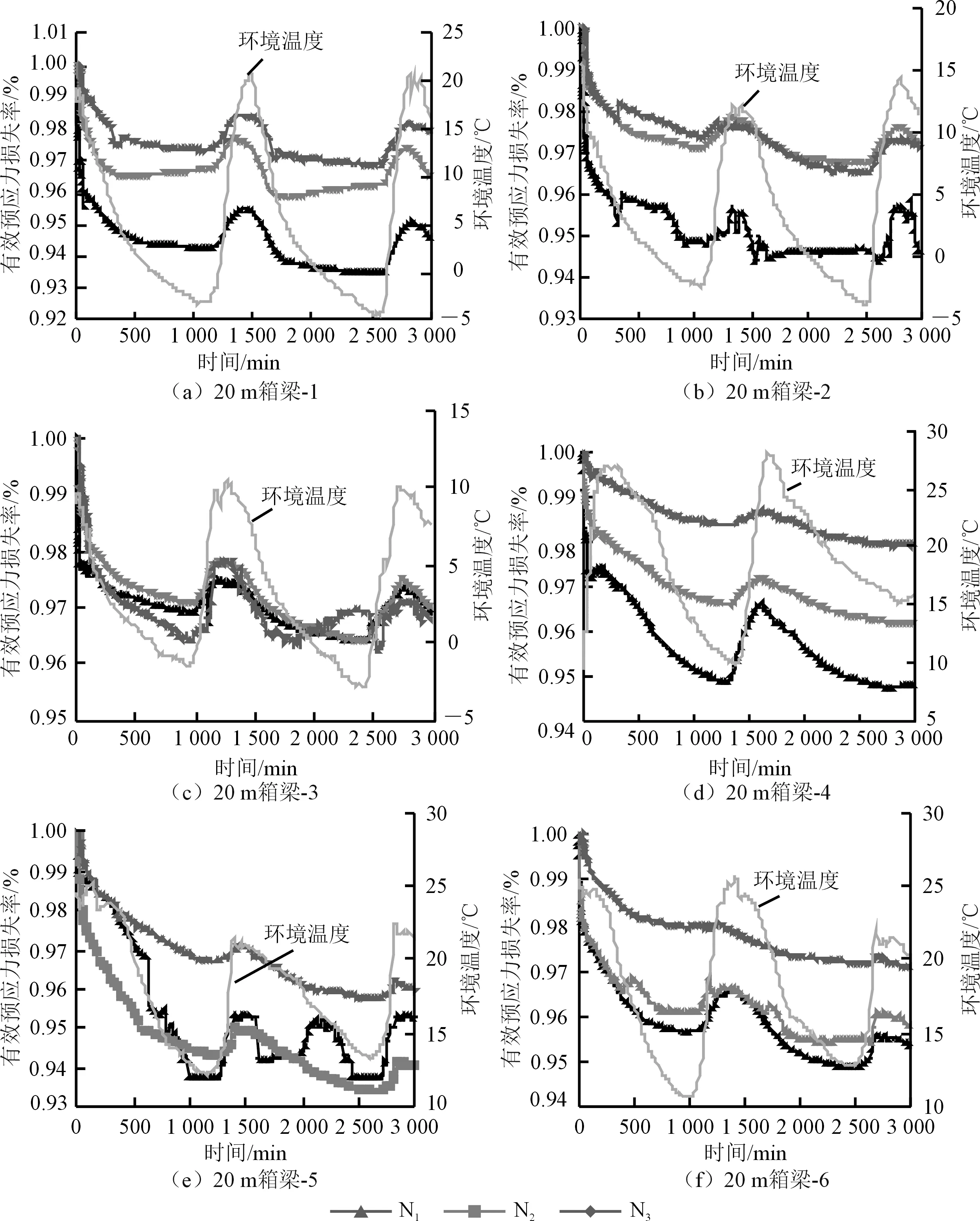
图4 测试数据统计

从图4可以看出：48 h内，预应力混凝土结构受一天内环境温度循环作用发生明显的波动，因此每束钢绞线内有效预应力值呈周期性正弦波形曲线衰减；先张拉完成的钢束的损失率比后张拉的钢束大。这是由于张拉钢束使梁体产生缩短变形，当后张拉的钢束对梁体施加预应力后，梁体进一步上拱变形，导致先张拉的钢束产生微小回缩，使其张拉力减小，其损失率比后张拉的钢束大。

基于现场测试结果，梁体内钢绞线锚下有效预应力损失率基本呈对数函数形式增长，前500 min损失较大，后期逐渐趋于平缓。

2.2 施工阶段预应力损失变化有限元模拟

考虑混凝土收缩徐变、钢绞线低松弛效应、夹片回缩量、混凝土弹性变形及孔道摩阻损失等影响因素，将48 h分为10个施工阶段，每个施工阶段时长为0.2 d；考虑系统初始温度为10 ℃，最终温度为25 ℃，建立计算模型(图5)，数值模拟计算结果如图6所示。

图5 有限元模型

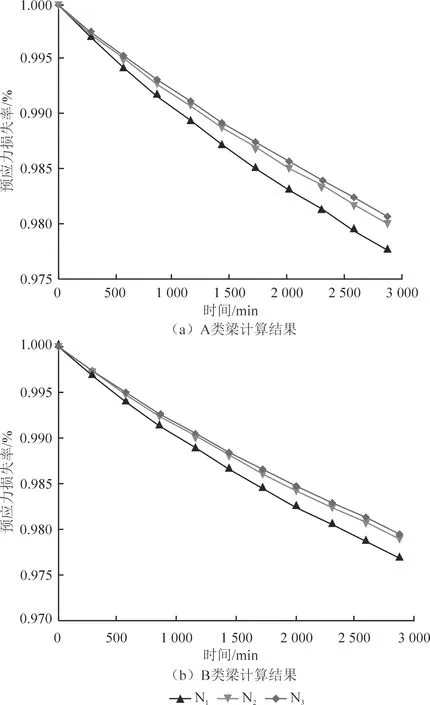
图6 有限元计算结果

将2种类型的梁体有限元计算结果取均值，同试验测试拟合结果进行对比，取0.2 d(即288 min)为一个时间节点，将48 h试验过程的结果整理成表2。

从表2可以看出：预应力损失率的实测值比数值分析结果大，最大相差3.43%。由统计数据可知，在目前预应力张拉施工过程中，规范规定的理论损失值偏小，需引起注意。

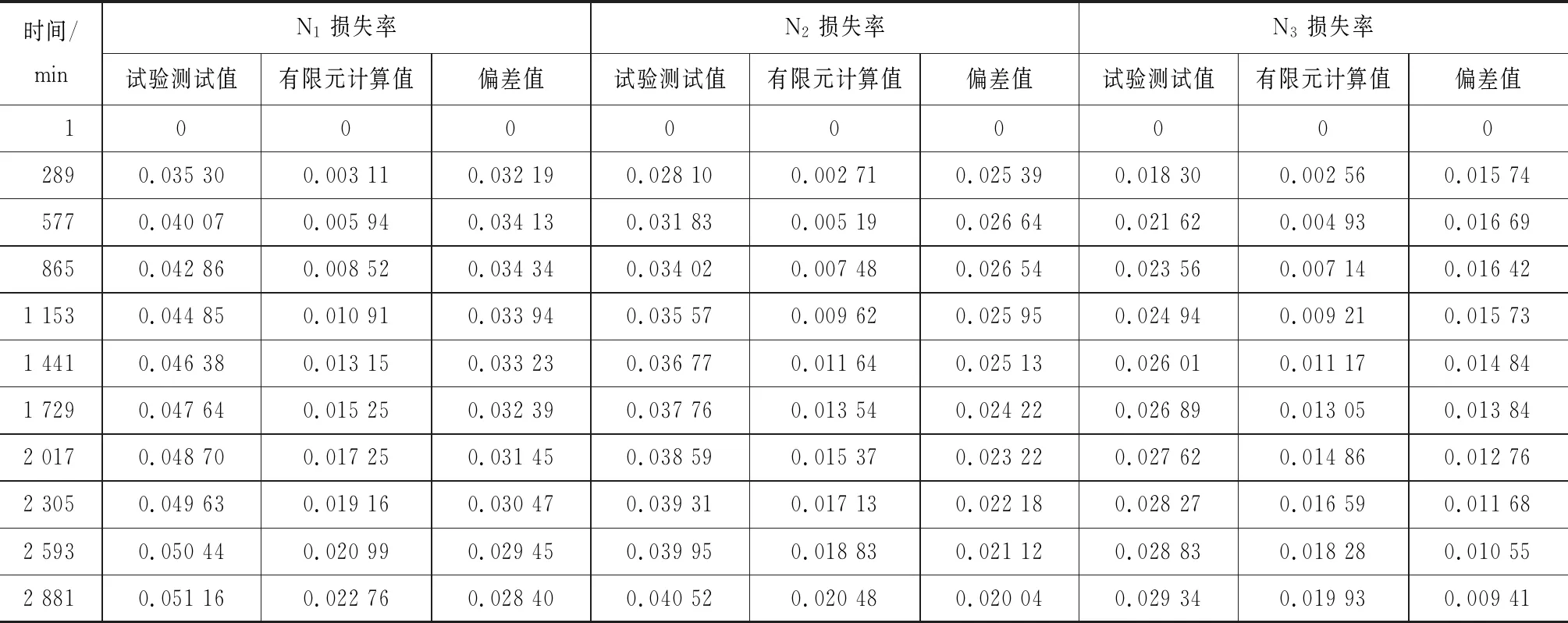
表2 试验测试值与有限元模拟损失率变化对比

2.3 张拉结束后48 h内时间效应修正

提取每个时间点的18根钢绞线的损失率数据，通过统计分析得到损失率的95%保证率的上、下限值，见图7。

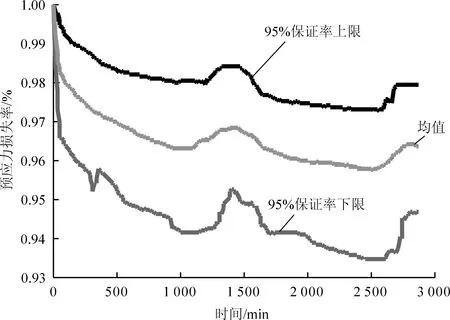
图7 48 h预应力损失率随时间变化的趋势

分别提取N1、N2、N3钢绞线损失率，建立各束钢绞线预应力损失变化数学回归模型，如图8所示。

拟合得到的N1～N3各束预应力损失率的数学模型表达式为

式中：k1～k3为各钢绞线预应力损失率；t为张拉后经过的时间(t>1 min)。

3 有效预应力的温度效应修正

预应力混凝土结构受一天内环境温度循环的作用会发生明显的波动，对于昼夜温差较大的地区，环境温度对于预应力值的影响程度也会更大，考虑环境温度效应的修正就具有十分重要的现实意义[13-17]。

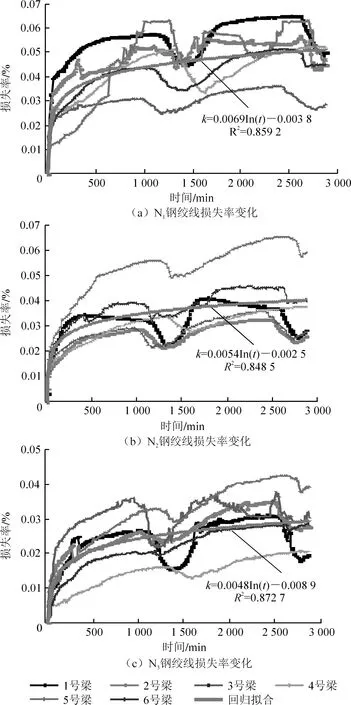
图8 钢绞线预应力损失率变化及线性拟合结果

选取试验梁张拉结束24 h后环境温度最高的13点至次日13点之间的一个温度循环(24 h)的锚下有效预应力值数据与温度值数据，分析相关变化关系，如图9所示。

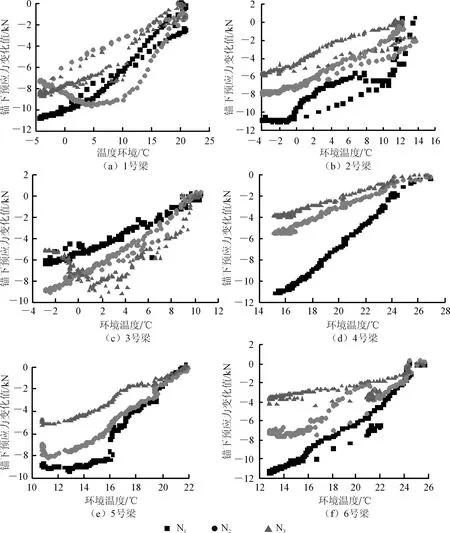
图9 24 h后的预应力与温度的关系

分析图9可以看出：在环境温度最高时，锚下有效预应力最大；当温度降低时，锚下有效预应力随之减少，基本呈线性关系；锚下有效预应力变化量ΔF与温度变化值ΔT的关系见图10。

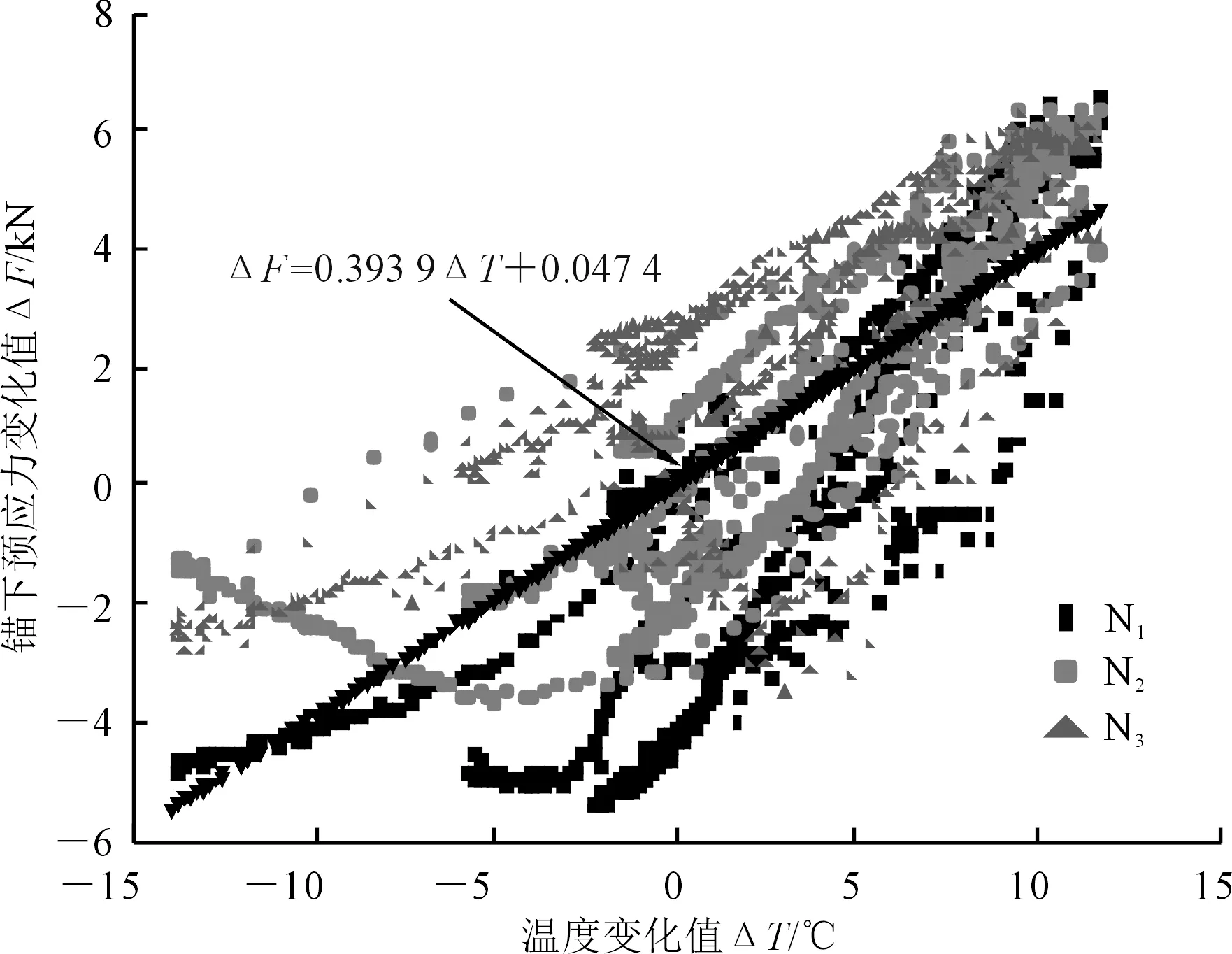
图10 张拉力随温度变化的模型

拟合得到考虑温度效应的锚下有效张拉力修正模型为

ΔF=0.393 9ΔT+0.047 4

(4)

4 结 语

(1)基于现场测试结果，通过拟合回归得到3种类型钢绞线预应力损失率数学模型表达式，该损失率模型呈对数函数形式变化，前500 min损失较大；分析48 h内的不考虑温度的预应力损失衰减规律，发现各钢束间预应力值离散性随时间的增加而增大。

(2)通过数值模拟施工阶段预应力钢绞线的变化规律，对比分析现场测试值和数值计算结果，发现实际测试中初期预应力损失较理论值明显偏大，随着时间增加，损失率均有放缓增长的趋势。

(3)损失率曲线存在周期性正弦波变化，该变化是由环境温度变化引起的，相比时间效应对锚下预应力的影响程度，温度对锚下有效预应力的影响较小；通过回归拟合得到了考虑温度效应修正的预应力变化值数学模型，可进一步对每时刻下的锚下预应力进行准确修正。