含运动副间隙的涡旋压缩机驱动轴承动力学仿真分析

赵 嫚，张 强，闫鹏举

（兰州理工大学石油化工学院，甘肃兰州730050）

1 引言

“节能降耗”是中国可持续发展的基本国策，涡旋压缩机作为一种新型容积式压缩机械，具有经久耐用、节能高效等优点，已被广泛应用于制冷与空调、各种气体压缩、增压泵等领域[1]。

转子系统良好的动力学特性是保障涡旋压缩机高效、可靠运行的关键[2]。从结构及承载方面的综合考虑，涡旋压缩机曲柄销与动涡盘轮毂处多采用滚针轴承联接。实际生产中转子系统构件的加工误差、装配误差以及磨损会导致转子系统的运动副产生大小不同的间隙；压缩机在运行过程中动涡盘受气体倾覆力矩的作用，使轴承随其发生倾斜，从而加剧了轴承的冲击碰撞及过摩擦损耗，导致转子系统机构动力学特性恶化[3]，因此对含运动副间隙涡旋压缩机动涡盘倾覆特性下，驱动轴承的动力学特性研究具有重要的工程应用价值。

国内外学者对含运动副间隙涡旋压缩机的动力学展开了多年的研究，并取得了一定的成果。文献 [4]基于虚拟样机技术对涡旋压缩机转子系统进行了动力学特性及有限元研究，施加气体力研究曲柄销与驱动轴承之间的单个间隙对压缩机动力学特性的影响，但其仅采用5个主轴转角下的气体力计算结果模拟压缩腔气体力变化，且未考虑动涡盘与防自转机构之间的间隙以及轴承与曲柄销之间不同间隙值大小的影响；文献 [5]针对小轴防自转机构涡旋压缩机进行了动平衡仿真，研究运动副间隙对涡旋压缩机动平衡的影响，但未考虑气体力作用下动涡盘倾覆所带来的影响。

本文基于虚拟样机技术以某卧式涡旋压缩机转子系统为研究对象，建立起含运动副间隙的涡旋压缩机转子系统动力学模型，根据计算结果在ADAMS软件添加气体力进行仿真，分析动涡盘倾覆下不同运动副间隙对驱动轴承动力学参数变化规律的影响，并根据仿真结果得出动盘倾覆下轴承的偏磨区域，为涡旋压缩机的优化提供了重要的理论参考。

2 涡旋压缩机转子系统的结构

图1 涡旋压缩机转子系统的结构

不同类型涡旋压缩机的转子机构会有一定差异，但大致结构组成相同。本文采用的某卧式涡旋压缩机转子系统如图1所示，主要由动涡盘、滚针轴承、十字滑环、大小平衡铁、曲轴等零件组成。当皮带轮带动曲轴旋转时，动涡盘在曲柄销的驱动下以及十字滑环防自转机构的限制下，相对静涡盘作公转平动使得压缩腔容积发生变化，完成压缩机的吸气、压缩和排气[6]。

3 含运动副间隙转子系统动力学建模

3.1 运动副间隙的矢量模型

首先应对运动副间隙进行正确的描述，本文引入一个间隙矢量eij来描述含间隙转动副中轴承和曲柄销的相对运动关系，即轴承和曲柄销之间连接点的相对位置可通过间隙矢量来表示，如图2所示，OXY为惯性坐标系。模型中间隙矢量的变化可以反映出动涡盘倾覆时，轴承与曲柄销之间是否发生接触[7]。

矢量模型中间隙大小可以用轴承内圈半径与曲柄销半径之差描述，则间隙为

式中rj——轴承内圈的半径

ri——曲柄销的半径

3.2 运动副间隙的接触碰撞力模型

国内外学者对含间隙机构动力学进行了广泛的研究并建立了许多运动模型，相比其他模型，二状态运动模型的仿真结果更贴近实验结果，这里采用二状态运动模型。

二状态运动模型中的非线性弹簧阻尼模型常应用于旋转铰的描述，这里选用该模型建立轴承与曲柄销的间隙接触碰撞模型，如图3所示，其广义形式可表示为

图2 运动副间隙矢量模型示意图

图3 非线性弹簧阻尼模型

式中Fn——法向接触力

Fk——弹簧恢复力

Fd——等效阻尼力

Kn——等效接触刚度

δ——法向穿透深度

δ˙——为法向相对速度

C（δ）——与δ有关的阻尼因子

m——指数，且m≥1

多体动力学软件ADAMS中Impact函数模型采用非线性弹簧阻尼器模型计算碰撞接触力。Impact函数的接触力计算公式为

式中K——接触刚度系数

δ——两构件之间的穿透深度

dδ/dt——构件的相对碰撞速度

n——≥1的力指数

Cmax——最大阻尼系数

dmax——使用Cmax计算出来的穿透边界的的深度

3.3 运动副间隙的摩擦力模型

这里选用修正的库伦摩擦力模型描述间隙铰处的摩擦力，其较为广泛地应用于碰撞模型的摩擦行为中，切向摩擦力计算公式为

式中 μd——铰接处滑动摩擦系数

cd——动态修正系数

υt——两构件的相对切向速度含间隙运动副处的轴承与曲柄销发生碰撞时，产生了接触碰撞力，该约束力可定义为Fc，并根据碰撞过程加入阶跃函数

则间隙处的约束力为

当轴承与曲柄销发生接触时，含运动副间隙转子系统的动力学方程为

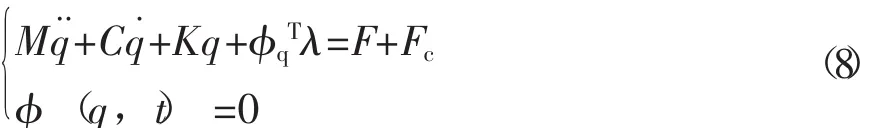
式中q——转子系统的广义坐标列阵

M——广义质量阵

C——广义阻尼阵

K——广义为刚度阵

φq——约束方程的雅克比矩阵

F——广义速度二次项以及力阵

λ——拉格朗日乘子

t——时间

4 含运动副间隙转子系统仿真模型的建立

4.1 转子系统三维实体模型的建立

ADAMS软件建模能力相对较弱，这里选用SolidWorks软件建立转子系统的实体模型。建立模型时应尽可能简单，以减少建模过程和转配过程中的工作量，比如去掉螺栓、油道、开孔等。样机干涉检查合格后，装配好的样机以x_t格式进行保存。该转子系统已通过理论平衡配平，达到动、静平衡，动涡盘质心理论上处于滚针轴承中心轴线上。滚针轴承与曲柄销连接处为含间隙的转动副，动涡盘与十字滑环配合处为含间隙的点线副。

4.2 转子系统动力学模型的建立

保存好的模型导入ADAMS中，根据模型设置恰当的单位、重力以及栅格大小，对机构中的每一个构件分别进行颜色设置、重命名、材料属性定义，各构件参数如表1所示。

根据转子系统实际工作情况对各构件施加驱动、约束和测量，其中理想旋转副采用转动副进行定义，含间隙的运动副采用接触副（Contact）进行定义。仿真时建立一个刚体圆环等效替代静涡盘，它起到限位作用，ADAMS/view里ground相当于机架体，转子系统各部件之间的约束关系见表2。

由动涡盘的受力分析可知，压缩机运行过程当中动涡盘会受到倾覆力作用，使滚针轴承随动涡盘出现倾斜趋势。根据计算结果，在动涡盘1/2齿高的基圆半径处添加气体倾覆力，使其动涡盘产生实际工况下的倾覆效果。在ADAMS中根据SPLINE函数定义单向力，并根据计算结果设置其大小和方向，其中力函数公式中的SPLINE样条拟合曲线根据气体力变化规律建立且随曲轴转角变化而变化，在SPLINE拟合方法对话框中选择Cubic Fitting Method选项[9]。

忽略压缩机启动阶段，设置皮带轮转速为2900 r/min，仿真步数定为5000步，仿真时间为0.1s。样机建模完成后进行自检以达到仿真要求[10]。参数设置完成后的转子系统虚拟样机模型如图4所示。

分析过程中所有部件假设均为刚体，为了保证滚针轴承模型在动力学分析中部件的几何结构不失真，避免发生零件接触穿透，在零件接触时采用Solid to Solid的接触形式。在接触卡片设置时采用Impact接触函数的算法，参数设置如表3所示。

表1 主要运动部件相关参数

表2 各部件之间的约束关系

5 动力学仿真结果与分析

根据曲轴机构加工等级，曲柄销公差范围为0.01～0.05 mm，则最终选取间隙值为0 mm（理想约束）、0.01 mm、0.03 mm、0.05 mm进行仿真和分析。十字滑环与动涡盘配合键槽处间隙取最大公差0.09 mm，动涡盘和十字滑环Contact接触，十字滑环另一侧凸键与机架体为理想点线约束。主轴承、副轴承与主轴铰接不含间隙。气体力随曲轴旋转发生周期性变化，仿真结果选择一个周期进行分析，图5所示为滚针轴承运动参数，图6所示为运动副接触碰撞力，图7所示为滚针轴承质心轨迹。

由图5（a） 可知，理想模型与含间隙模型中的滚针轴承位移曲线几乎重合，这表明动涡盘倾覆下间隙对滚针轴承的位移几乎没有影响。图5（b） 与图5（d） 可知，间隙的存在使得轴承的速度与角速度相对理想状态出现小的波动，间隙值越大，速度波动峰值越大，间隙值0.05 mm模型的速度最大峰值相对理想状态下偏差约为4.85%，但速度曲线整体的趋势相同，所以间隙对滚针轴承的速度与角速度的影响也比较小。但由图5（c）与图5（e） 可知，理想模型滚针轴承的加速度和角加速度曲线很光滑，但含间隙模型的加速度与角加速度出现脉冲式波动且瞬时峰值很大，当间隙尺寸增加到0.05 mm时，加速度曲线相比理想模型出现明显偏差，最大幅值约为理想模型的1.76倍。整体而言，无论是幅值还是波动相比理想模型都相当大，说明间隙对滚针轴承的加速度与角加速度的影响非常大，对转子系统的运行精度和可靠性影响较为显著[11]。

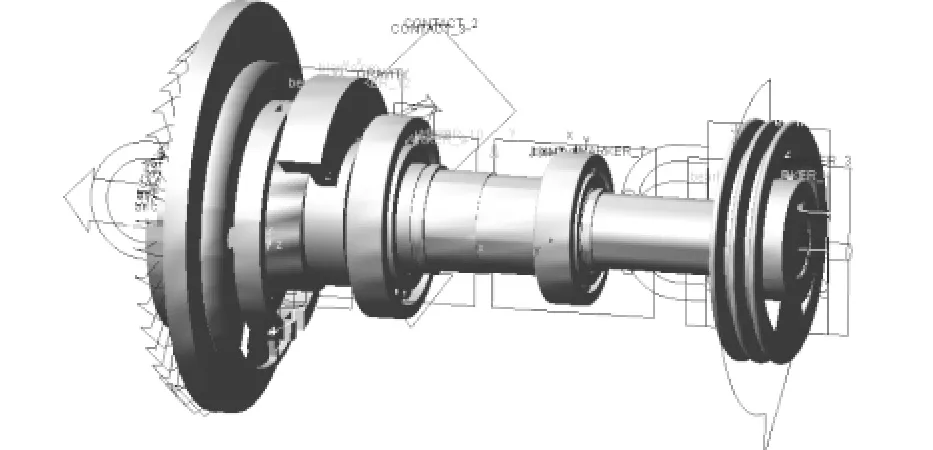
图4 转子系统连接关系

表3 仿真参数

由图6可知，含间隙模型中的接触碰撞力频次和数值力明显大于理想模型，对比图5（c）可发现间隙铰处接触碰撞力的变化规律与加速度的变化类似，间隙大小变化的对滚针轴承的动态特性影响很大。具体表现为：随间隙值的增加，曲柄销与滚针轴承接触碰撞力力的波动幅度增大但波动频率相对减小。间隙值0.05 mm的模型的碰撞力相对理想模型明显变大，同一时刻下二者最大差值约1684N，是理想状态接触力的2.53倍。一个曲轴旋转周期内，倾覆力大小在689.57～811.48N区间内变化，接触碰撞力在排气角的位置出现峰值，受力呈现波浪形趋势，即需要关注波峰值时轴承运动位置以及其受力情况，可以对轴承动力学做出预测。

由图5和图6可知，运动副的间隙对滚针轴承的位移和速度的变化影响相对较小，对滚针轴承加速度和接触碰撞力的影响较大，且间隙值越大影响越明显。这是由于运动副间隙值较小时，曲柄销在滚针轴承发生碰撞前自由运动的时间相对较短，发生碰撞的时间也相对较短，而轴承位移和速度的改变需要时间，因此间隙模型的位移和速度相比理想模型变化不明显，但间隙铰处的接触碰撞在极短时间内完成，因此轴承加速度和间隙铰处碰撞力的曲线图走势类似，二者均呈现出脉冲式波动且数值大小不断变化。但是运动副间隙增大时，轴承与曲柄销发生碰撞前的运动时间会相对增加，则二者碰撞的次数会降低但碰撞前的速度会增大，导致运动副间隙处的加速度和接触碰撞力增大[12]。

图5 滚针轴承运动参数曲线图

图中7（a） 加粗实线表理想模型轴承质心运动轨迹，在不同间隙模型下间隙越大轨迹偏离距离越大；图7（b） 可以很清楚看到间隙模型的质心轨迹在理想轨迹圆内发生碰撞，在轨迹圆外未发生碰撞。图7（b） 中横坐标-50.0041 mm至-50.6475 mm范围内，间隙模型下轴承运动轨迹明显进入理想运动轨迹，即该处发生较为严重的碰撞。计算发现，以该模型动涡盘涡齿正面建立平面二维坐标系，该碰撞区域为-136.5°至-155.46°范围内。该卧式涡旋压缩机的排气角为坐标系-126°的位置，此处压缩机开始排气，压缩腔中气体力最大。即滚针轴承发生偏磨区域在排气后19.11°范围内，间隙与运动惯性使得磨损区域滞后于最大气体力位置，此时碰撞力也处于峰值状态加速了磨损，与实际情况相符具有指导意义。

6 结论

（1） 间隙的存在对滚针轴承位移几乎没有产生影响；对滚针轴承速度的影响较小；对滚针轴承加速度的影响较大，曲线出现脉冲式的波动；间隙的存在使轴承与曲柄销的碰撞次数较频繁，并且碰撞力幅值随着间隙值的增大而增大。

（2） 滚针轴承存在固定偏磨区，为排气角后19.11°范围内。间隙值越大，滚针轴承质心运动轨迹的偏差越大，滚针轴承的磨损加剧，转子系统的可靠性和运行稳定性变差。

（3）动涡盘倾覆的计入更真实地反映了涡旋压缩机转子系的动力特性，仿真结果表明压缩机设计时应严格选用滚针轴承处的配合公差，以减少动涡盘倾覆造成的偏磨影响，提高轴承使用寿命。