基于改进多元线性回归的股票价格预测模型

李俊豪

摘 要：当前股票市场价格波动剧烈，不论是专业股票投资者以及相关从业人员还是二级市场中的散户都希望找到一条行之有效的路径进行股票价格预测，这不仅能帮助投资者控制风险，也可以帮助其减少不必要的损失。本文以当前比较流行的多元线性回归法为基础，并使用因子分析将这一方法进行改进对贵州茅台（SHSE. 600519）这一支股票进行股价预测，最终通过比较预测效果，推行出适用于该股票的股价预测模型。

关键词：量化投资;多元线性回归;因子分析;股价预测;数学建模

0 引言

事实上，量化投资就是使用数学的方法与手段在经济现象中找到数据存在的内在联系，通过K线图的观察，可以看到当前某些股票有明显的时间序列上的线性关系，那么进而可以大胆的假设，实际上股票价本身是否与自身的各个指标之间有着较强的线性关系。本文建立了多元线性回归模型，把股价作为被解释变量，其他影响因素作为解释变量，进行模型模拟。[1]

我们在对该模型进行共线性诊断时会发现，开盘价、最高价、最低价、收盘价、总手数、次日开盘价这些自变量间存在严重的多重共线性，影响了模型的预测效果。事实上，计量经济学理论给出了多种消除多重共线性有多种处理方式，本文选择使用较为简便的方式，即因子分析来消除多重共线性。在进行因子分析后，我们将多个解释变量最终分为两个因子，分别是价格因子和数量因子，以这两个因子为自变量，次日收盘价为因变量进行多元线性回归，得到的回归方程模型进行预测的结果远远优于之前的回归模型。[2]

本文最终使用东方财富软件上的日K线图上的数据作为数据来源，选取贵州茅台（SHSE.600519）这只绩优的白马股作为目标股票，把2018.10.30-2019.4.17共计114个交易日作为模型建立的训练集，把2019.4.18-2019.4.30共计9个交易日作为模型检验回测期。

1 多元线性回归

1.1 模型建立

多元线性回归使用当日开盘价、最高价、最低价、总手数，次日开盘价为自变量，次日收盘价为因变量作出多元线性方程进行求解预测。

设次日收盘价为Y，当日开盘价为X1，最高价为X2，最低价为X3，收盘价为X4，总手数为X5，次日开盘价为X6，可以得到多元回归方程为：

Y=-8.099-0.082X1+0.296X2+0.412X3-0.724X4+

3.722*10-7X5+1.112X6

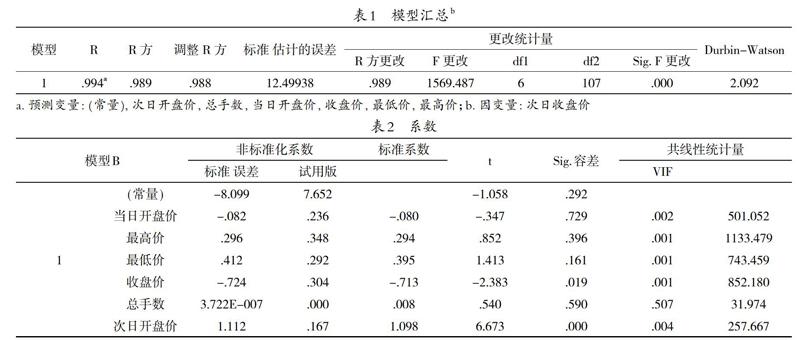
其中R2为0.988，说明数据的拟合程度相当好，并且根据DW检验数值显示，由于DW值在2左右，该模型不具有自相关性。

1.2 模型预测

将各解释变量的数值代入多元线性回归方程中有：

Y=-8.099-0.082X1+0.296X2+0.412X3-0.724X4+3.722*10-7X5+1.112X6

次日收盘价（2019.04.18-2019.04.30）的预测值是：

942.59，948.55，961.15，962.3，981.01，973.27，956.91，956.03，967.04

与观察值的绝对误差分别为：2.91，4.01，11.95，12.65，11.01，20.9，11.91，15.94，9.96

平均绝对误差为：11.22

平均绝对误差百分比：1.18%

可以看到所得到的模型的预测效果非常好，绝对误差的百分比只有1.18%，估计值几乎已经无限接近于实际观察值。

2 模型改进

2.1 模型建立

由表2可以看到该模型具有非常強的多重共线性，VIF值远远大于10，所以本文采用因子分析法来减少多重共线性对模型的冲击，首先要进行因子分析的前提条件假设。

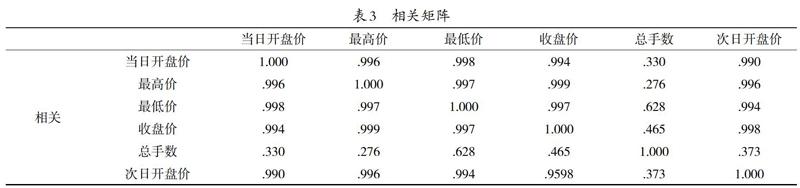
可以看到绝大多数的相关系数均超过了0.6，并且由接近70%的相关系数在0.9以上说明当前各变量之间有较强的相关性。基于这样的强相关性，可以看出当前各组数据比较适合进行因子分析，但是本文还对该组数据进行了其他相关检验保证数据的合理性。

根据检验结果可以看出由表知巴特利特球度检验的检验统计量为2604.772，该观测值较大，且对应的概率P值小于给定的显著性水平，且KM0值为0.812，表明原有变量适合作因子分析。

在基于该模型适合做因子分析的情况下，本文使用spss软件进行了数据的因子分析：

两个因子对总变量的解释程度达到了99.762%，解释效果良好，可以形成两个因子。

由此就得到了两个因子，第一个因子的方差贡献率是5.013，第二个因子的方差贡献率是0.973。从而可

以对两个因子进行命名，因子一：价格因子，因子二：数量因子。

F1=0.996X1+0.999X2+0.997X3+0.999X4+0.192X5+0.997X6

F2=-0.063X1-0.016X2-0.065X3-0.027X4+0.981X5-0.018X6

2.2 改进模型回测

根据下表可以看到调整后的R方为0.984，说明模型拟合程度相当好，并且significant-F值为0.000<0.05。该模型经过DW检验后，DW值为1.761在2附近，可以认为不存在自相关性。

根据所提供的系数可以得到回归方程：

Y=683.963+113.327F1+11.08F2

将所得数据带入上述回归方程，并与原股价进行对比，最终得到相应的股票价格变动只有平均绝对误差百分比：0.277%。

这一结果可以说非常贴近于现实的股票价格，预测模型基本通过检验并且模型的计量经济学检验，统计检验上都显著性通过，模型建立效果比较好。

3 模型缺陷与总结

本文模型采用了经典的多元线性回归模型，在得到较好的回归模型拟合结果后，充分考虑了多重共线性这一问题，使用因子分析极大程度的解决了模型的多重共线性，保证了模型的VIF<10，所得到的最终模型回测比较成功，成功的预测了贵州茅台（SHSE.600519）的股价，具有一定的实战意义，给广大投资者以及基金管理人员提供了预测股票价格的新思路。

但是本次模型依然不够完善，因为股票市场是充满变化的市场，本文所预测的股价时间段是贵州茅台股价处于上涨阶段的突破行情，不一定适用于震荡行情，或是连续下跌行情，并且本文只是从纯粹的技术面进行股价分析，没有考虑公司的基本面变化以及消息面、资金面对于模型的冲击，所以模型依旧不够完善，希望各位同仁批评指正，完善股价预测模型。

参考文献：

[1]郭伟杰.卖空机制对股价收益率波动性的影响——基于AH股公司股价收益率的实证研究[J].现代商业，2009.

[2]贾宗英.区域林业社会化服务体系评价研究[D]. 南京：南京林业大学，2010.