Asymptotic Dynamics of Non-Autonomous Modified Swift-Hohenberg Equations with Multiplicative Noise on Unbounded Domains

Mohamed Yagoub Abaker(巴吉),LIU Tingting(刘亭亭),MA Qiaozhen(马巧珍)

( 1.College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,china;2.Department of Mathematics,College of Education,Rumbek University of Science and Technology,Rumbek,South Sudan)

Abstract: We investigate the dynamical behavior of the stochastic non-autonomous modified Swift-Hohenberg equation with time-dependent forcing term and multiplicative noise on R2.In order to overcome the difficulty that Sobolev embedding are not compact in the unbounded domain,we first define a continuous cocycle associated with the problem in L2(R2),and make some uniform estimates on the tails of solutions for large space variables.With the aid of uniform estimates of solution,we verify the pullback asymptotic compactness of the random dynamical system,and further obtain the existence of random attractors.

Key words: Random attractor;Swift-Hohenberg equation;Non-autonomous random dynamical system;Continuous cocycle

1.Introduction

We consider the following modified Swift-Hohenberg equation on R2perturbed by a wiener-type multiplicative noise.

whereu=u(x,t) is a real function on R2,∆is the laplacian operator with respect to the variablex∈R2,aandbare arbitrary constants.The functionf(x,t)∈L2loc(R;L2(R2)) is an external force.W(t) is an independent two sided real-valued wiener processes on probability space (Ω,F,P),whereΩ={ω∈C(R,R):ω(0)=0},Fis the Borelσ-algebra induced by the compact-open topology ofΩ,P is the corresponding wiener measure onF,and◦denotes the Stratonovich sense in the stochastic term.In case ofb,f=0,and we omit the noise term,then (1.1) is the usual Swift-Hohenberg equation.

The Swift-Hohenberg equation[18]is a partial differential equation,and it takes the form

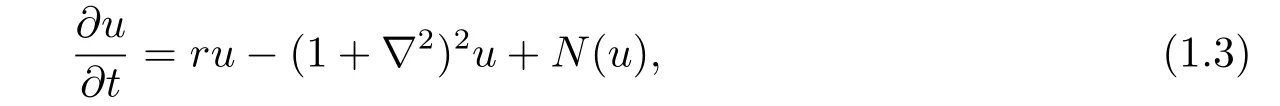
whereu(x,t) is a scalar function defined on the line or the plane,ris a real bifurcation parameter andN(u) is smooth nonlinearity.Swift and Hohenberg proposed this model for the convective instability in the Rayleigh-Bénard convection.This equation plays a central role in studying of a pattern formation.It’s an important equation in different branches of physics,spatially in thermal dynamics[12,15−16].Doelman and Stanstede[6]proposed the following modified Swift-Hohenberg equation for a pattern formation system

whereaandbare arbitrary constants.In case ofb=0,(1.4) becomes the usual Swift-Hohenberg equation,and the additional termb|∇u|2aries in the study of various pattern formation phenomena involving some kind of phase turbulence of phase transition that breaks the symmetryu→−u.Both theb|∇u|2andu3terms are nonlinearities,andbis the parameter controlling the strength of the quadratic nonlinearity.A detailed analysis of a pattern formation systems reveals that pattern formation is governed by order parameters,whose spatiotemporal behaviour is determined by nonlinear partial differential equation.As the effect of thermal fluctuation on the onset of the convective motion in the Bénard system is considered in [18],the stochastic local Swift-Hohenberg equation with additive noise is proposed by Swift and Hohenberg as

SONG et al.[17]used an iteration procedure,regularity estimates for the linear semigroups and a classical existence theorem of global attractor,to prove that a modified Swift-Hohenberg equationut=−∆2u+g(u) possesses a global attractor in Sobolev spaceHkfor allk≥0 which attracts any bounded subsets ofHkin theHk-norm.

Furthermore,a local stochastic Swift-Hohenberg equation driven by multiplicative noise when the effects of small possible noise fromµis consider by Blmker[2]

whereσ >0 andξ=is the generalized derivative of a real-value Brownian motion.For more physics background,see [1-7]and the references therein.

Recently,non-autonomous Swift-Hohenberg equation was studied by many researchers(see [9,11,13-14,20-21]).WANG and DU[21]obtained the existence of pullback attractor for modified Swift-Hohenberg equation on unbounded domain with forcing term and additive noise.GUO[10]investigated the dynamical behaviour of modified Swift-Hohenberg equation with multiplicative noise but without any external force.In this paper we will study the existence of random attractors for the non-autonomous stochastic equation with the timedependent external force and multiplicative noise.

We try to organize this paper as follows.In Section 2,we give some basic definitions concerning the random attractors for dynamical system which are important to get our main result.In Section 3,we transform the stochastic equation into deterministic one with random parameter and come into being a continuous cocycle.In Section 4,we show the uniform estimates of the solution.Finally,in Section 5,we prove the existence of random attractors.

2.Preliminaries and Abstract Results

In this section,we recall some basic concepts related to RDS and a random attractor for RDS in [4-5,8,19],which are important for getting our main results.Let (Ω,F,P)be a probability space and (X,d) be a polish space with the Borelσ-algebraB(X).The distance betweenx∈XandB⊆Xis denoted byd(x,B).IfB⊆XandC⊆X,the Hausdorff semi-distance fromBtoCis denoted byd(B,C)=supx∈B d(x,C).

Definition 2.1(Ω,F,P,(θt)t∈R)is called a metric dynamical system ifθ:R×Ω→Ωis (B(R)×F,F)-measurable,θ0is the identity onΩ,θs+t=θt ◦θsfor all s,t∈R andθ0P=P for all t∈R.

Definition 2.2A mappingΦ(t,τ,ω,x):R+×R×Ω×X→Xis called continuous cocycle onXover R and(Ω,F,P,(θt)t∈R),if for allτ∈R,ω∈Ωandt,s∈R+,the following conditions are satisfied:

i)Φ(t,τ,ω,x):R+×R×Ω×X→Xis a (B(R+)×F,B(R)) measurable mapping;

ii)Φ(0,τ,ω,x) is identity on X;

iii)Φ(t+s,τ,ω,x)=Φ(t,τ+s,θsω,,x)◦Φ(s,τ,ω,,x);

iv)Φ(t,τ,ω,x):X→Xis continuous.

Definition 2.3Let 2Xbe the collection of all subsets ofX,a set valued mappingis called measurable with respect toFinΩifD(t ω) is a(usually closed) nonempty subset ofXand the mapping(X,B(τ,ω)) is (F,B(R))-measurable for every fixedx∈Xandτ∈R.LetB={B(t,ω)∈D(t,ω):τ∈R,ω∈Ω} is called a random set.

Definition 2.4A random bounded setB={B(τ,ω):τ∈R,ω∈Ω}∈Dof X is called tempered with respect to{θ(t)}t∈Ω,if for P-a.eω∈Ω,

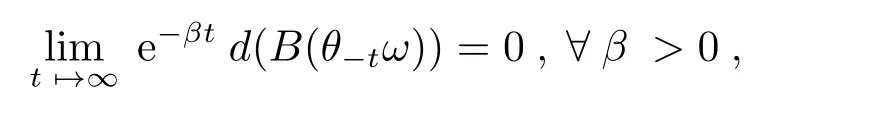
where

Definition 2.5LetDbe a collection of random subset ofXandK={K(τ,ω):τ∈R,ω∈Ω}∈D.ThenKis called an absorbing set ofΦ∈Dif for allτ∈R,ω∈ΩandB∈D,there exists,T=T(τ,ω,B)>0 such that

Definition 2.6LetDbe a collection of random subset ofX.ThenΦis said to beD-pullback asymptotically compact inXif for P-a.eω∈Ω,{Φ(tn,θ−tnω,xn)}∞n=1has a convergent subsequence inXwhentn→∞andxn∈B(θ−tnω) with{B(ω)}ω∈Ω∈D.

Definition 2.7LetDbe a collection of random subset ofXandA={A(τ,ω):τ∈R,ω∈Ω}∈D.ThenAis called aD-random attractor (orD-pullback attractor ) forΦ,if the following conditions are satisfied:for allt∈R+,τ∈R andω∈Ω,

i)A(τ,ω) is compact,and(x,A(ω)) is measurable for everyx∈X;

ii)A(τ,ω) is invariant,that is

iii)A(τ,ω) attracts every set inD,that is for everyB={B(τ,ω):τ∈R,ω∈Ω}∈D,

wheredXis the Hausdorff semi-distance given by

for anyY∈XandZ∈X.

Remark 2.1Let(Ω,F,P)be a probability space with wiener measure P and the wiener shift (θt)t∈Rbe defined by

Then (Ω,F,P,(θt)t∈R) is an ergodic metric dynamical system.

Lemma 2.1[5]LetDbe a neighborhood-closed collection of(τ,ω)-parameterized families of nonempty subsets ofXandΦbe a continuous cocycle onXover R and(Ω,F,P,(θt)t∈R).ThenΦhas a pullbackD-attractorAinDif and only ifΦis pullbackD-asymptotically compact inXandΦhas a closed,F-measurable pullbackD-absorbing setK∈D,and the unique pullbackD-attractorA=A(τ,ω) is given by

3.Cocycles of the Swift-Hohenberg Equation on R2

Consider the probability space (Ω,F,P),where

LetFbe Borelσ-algebra induced by the compact-open topology ofΩand P be the corresponding wiener measure on (Ω,F).We define a group{θt}t∈Racting on (Ω,F,P) and the time shift by

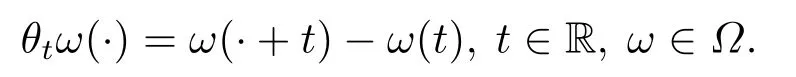
Then (Ω,F,P,{θt}t∈R) is a parametric dynamical system.

The original equation (1.1) can be written as follows

To study the dynamical behavior of problem(1.1)-(1.2),we need to convert the stochastic equation with a random multiplicative term into non-autonomous deterministic one with a random parameter.Now,we introduce an Ornstein-Uhlenbeck processz(θtω) driven by the Brownian motion,which satisfies the following Itequation

Then,the solution of (3.2) is unique and given by

By[1,7],the random variable|z(θtω)|is tempered and there is an invariant set⊆Ωof full P measure such thatz(θtω)=z(t,ω) is continuous intfor everyω∈.For convenience we shall writeasΩ.We put in the consideration the following properties:

Ifuis the solution of equation (1.1),we let the variable

Then

Thus,the equation (1.1) transforms into the following system:

Fort >τ,τ∈R andx∈R2,the equation (3.5) is a deterministic equation with random parameters.

By Fatou-Galerkin methods and some a priori estimates,we can show that iffandvτare given satisfyingf∈L2loc(R,L2(R2)),vτ∈L2(R2),then we can obtain a unique solution,that is for P-a.eω∈Ω,τ∈R andv(τ,τ,ω,vτ)=vτ,vτ∈L2(R2),and for everyT >0,v(·,τ,ω,vτ)∈C([τ,∞),L2(R2))∩L2((τ,τ+T);H1(R2)).For everyt≥τ,letu(t,τ,ω,uτ)=v(t,τ,ω,vτ)ez(θtω)withuτ=vτez(θτω).Then we obtain thatuis continuous and (F,B(L2(R2))-measurable inω∈Ω.

Define a cocycleΦ:R+×R×Ω×L2(R2)→L2(R2),and let

wherevτ=uτe−z(θ−τω).Then we can check thatΦis a continuous random cocycle associated with equation (1.1) onL2(R2) over (R,{θt}t∈R) and (Ω,F,P,{θt}t∈R),where{θt}t∈Ris a family of shift operator on R such thatθt(τ)=t+τ.

Provided that D is a collection of tempered random subsets ofL2(R2),we will prove the existence of an absorbing set inL2(R2).LetBbe a bounded nonempty subset ofL2(R2),and

LetD={D(τ,ω):τ∈R,ω∈Ω} be a family of subset ofB,which satisfies

whereλis a positive constant.

For the external forcef(x,t),we assume that

From (3.9),we deduce that

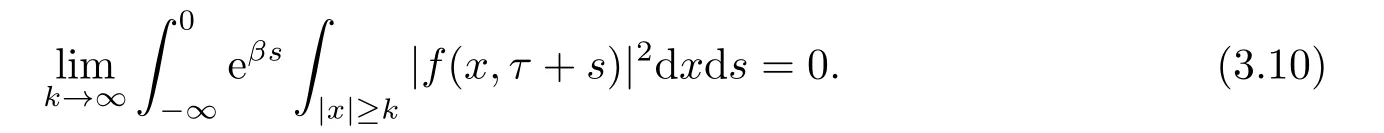
Lemma 3.1[14](Gagliardo-Nirenberg inequality) LetΩbe an open bounded domain of Lipschitz class in Rn.Assume that 1≤p,q≤∞,r≥1,0≤θ≤1,and let

Then the following inequality holds

Here,cis an arbitrary positive constant,which may change it’s value from line to line or even in the same line.

For notation we haveL2(R2) is the Hilbert space with usual inner products and norms,(·,·),‖·‖,where(u,v)=u(x)v(x)dx.AlsoHσ(R2)is the Sobolev space{u∈L2(R2),Dku∈L2(R2),k≤σ} with norm‖.‖Hσ=‖.‖σ.

4.Uniform a Priori Estimates of Solution

In this part,we show uniform a priori estimates of a solution for the stochastic local modified Swift-Hohenberg equation.

Lemma 4.1Under the assumptions in (3.9),for everyτ∈R,ω∈Ω,D={D(τ,ω):τ∈R,ω∈Ω}∈D,there exists,T1D=T(τ,ω,D)>0 such that for allt≥T1D,the solution of problem (3.5) satisfies

where

M(ω) is a tempered random variable.

ProofTaking the inner product of equation (3.5) withvinL2(R2),we have

Applying the Hölder inequality and theϵ-Young inequality,we have

Now,we deal with the last term on the right hand side of(4.2).By the Hölder inequality,the Gagliardo-Nirenberg inequality withk=1,n=2,p=r=4,m=q=2,0<θ

Substituting (4.3)-(4.5) into (4.2),we obtain that

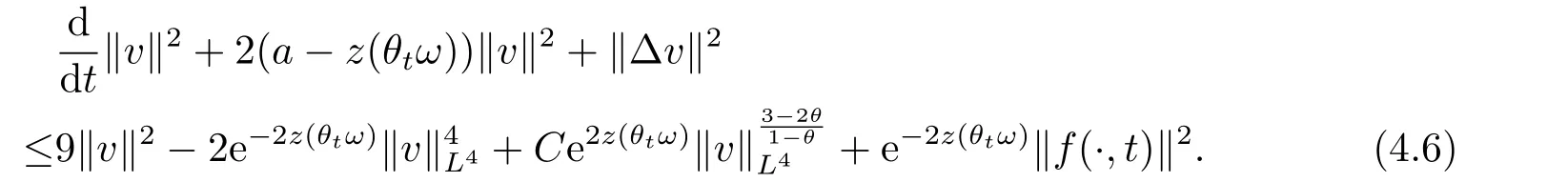
Namely for someβ >0,we have

Since 3<<4(0<θ <),and the properties ofz(θtω),there exists a random variableM(ω)>0 such that

Then we have

By the Gronwall inequality we have

Replacingωwithθ−τωin (4.10) we get

Since|z(θtω)|is stationary and ergodic,from (3.3) we can get there existsT1D >0 such that for allt≥T1D,

It follows that

So there exists a random variableρ1(τ,ω),for P-a.e.ω∈Ωandt>T1D,

then we can get‖v(τ,τ−t,θ−τω,vτ−t‖2≤C(1+ρ1(τ,ω)).

Lemma 4.2Under the assumptions in (3.9),for everyτ∈R,ω∈Ω,D={D(τ,ω):τ∈R,ω∈Ω}∈D,there existsT2D=T(τ,ω,D)>0 such that for allt≥T2D,and there holds

where

ProofMultiplying equation (4.9) bywe get

Multiplying (4.18) by and omitting the first term yield that

By substitutingτforin (4.11),we get

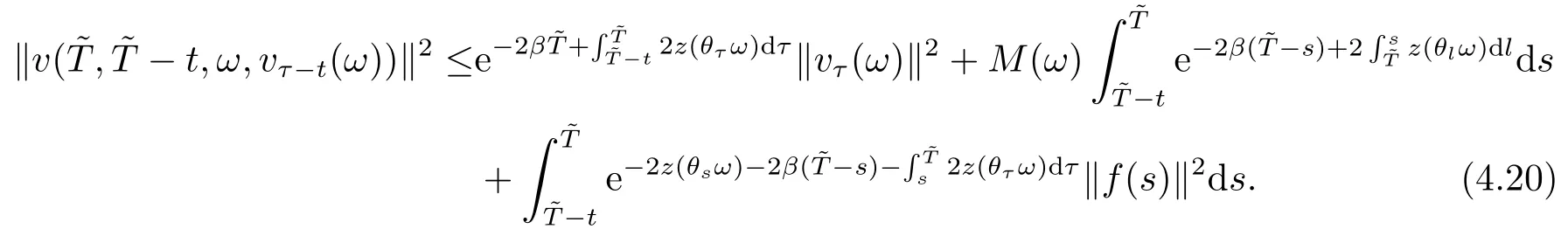
Substituting (4.20) into (4.19),we have

Replacingωbyθ−τωin (4.21),we obtain

To get the desired result,we substituteforτandτforτ+1 in (4.22) as follows:

Then we have

Sincet≥T1D,according to the properties ofz(θtω),when−1≤s−τ−1≤0,we infer that

Then,from (4.24) and (4.25),we prove that there exists a random variableρ(τ,ω) andT2D≥0 such that,for P-a.e.ω∈Ωand allt≥T2D,

which completes the proof.

Then,similar to the proof of Lemma 4.1 in [10],we can also get the result.

Lemma 4.3Under the assumptions in (3.9),for everyτ∈R,ω∈Ω,D={D(τ,ω):τ∈R,ω∈Ω}∈D,there existsT3D=T(τ,ω,D)>0 such that for allt≥T3D,and there holds

where

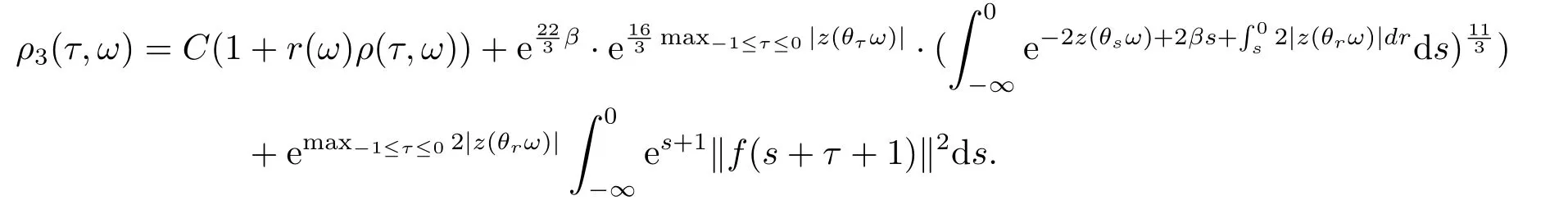
Lemma 4.4Iff∈L2loc(R,L2(R2)),vτ∈L2(R2).Then,for anyt >0,P-a.e.ω∈Ω,τ∈R andD={D(τ,ω):τ∈R,ω∈R}∈D,there existsTD=T(τ,ω,D,η)>1 andK=K(τ,ω,η)≥1 such that for anyt≥TD,the solutionvof equation (3.5) withωreplaced byθ−τωsatisfies

wherevτ−t∈D(τ−t,θ−τω).

ProofLetθbe a smooth function defined on R+,such that 0≤θ(s)≤1 for alls∈R+,and

Then there exists a positive constantCsuch that|θ′(s)|≤Cfor alls∈R+.For convenience,we write

Taking the inner product of (3.5) withθkvinL2(R2),we have

For the terms of (4.28),by the Hölder inequality and theϵ-Young inequality,we obtain

Then,from (4.29)-(4.33) it follows that

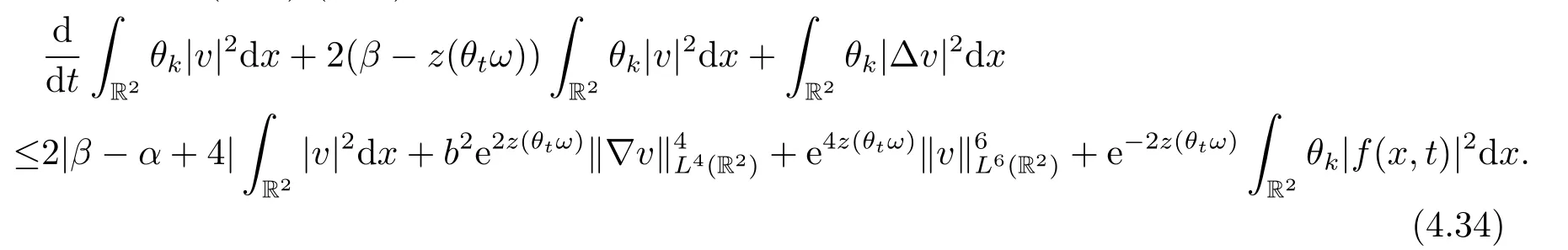
By the Gagliardo-Nirenberg inequality,we know

and

Combining with (4.35)-(4.36) we finally get

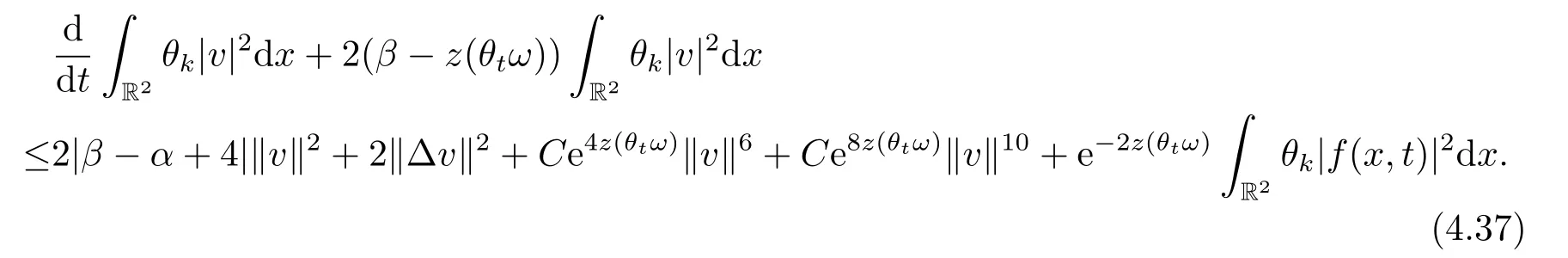
By applying the Gronwall inequality to (4.37) on [τ−t,τ]

Replacingωbyθ−τωin (4.38),we obtain

For any initial datavτ−t∈D(τ−t,θ−tω),we have

So for an arbitrarily givenη >0,there existsT3=T3(τ,ω,D,η),such that for allt≥T3,

By Lemma 4.1 and Lemma 4.3,similar to (4.12) and (4.14) for allt≥T3,we obtain

Finally,from the condition of (3.10),there existsk1=k1(τ,ω)>1,such that fork >k1,we have

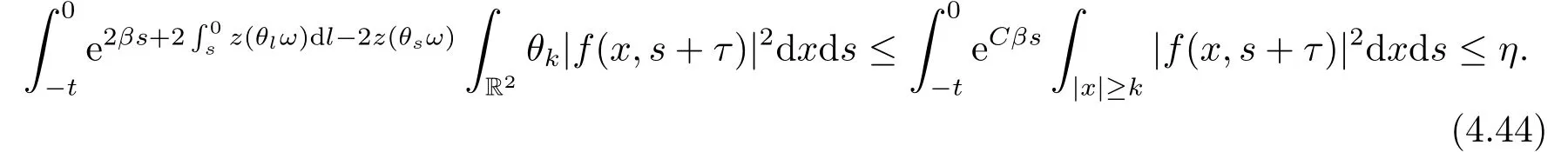
Then it holds that for allk >k1,t≥T3,

From (4.45),there existsk2=k2(τ,η)≥k1such that for allk≥k2,t≥T2,

Then the proof is completed.

5.Existence of Random Attractor

Theorem 5.1Suppose that (3.9)-(3.10) holds.LetDbe defined in (3.8).Then the continuous cocycleΦassociated with the problem (1.1) possess a uniqueD-random attractorA={A(τ,ω):τ∈R,ω∈Ω} in the initial spaceL2(R2).

ProofWe haveτ∈R,ω∈ΩandD∈D.Define

Letη >0.From (4.1) there existsT1=T1(τ,ω,D,η) and a ballBL2(R2)(0,C(τ,ω,η))centred at zero with radius less than or equal toC(τ,ω,η) such that

From the compact of Sobolev embedding in the bounded domain,for everyη >0 there exists a finiteη4−netinL2(QK) covering(τ,ω)QK.Therefore

wherekL2(·)is non-compact measure inL2(QK).By Lemma 4.3,there existsT2=T2(τ,ω,D,η)andK(τ,ω,D,η) such that

T=max{T1,T2}.By additive property of non-compact measure,we have

Therefore,by the arbitrariness ofη,Φis omega-limit compact inL2(R2).

By the inequality (4.26) in Lemma 4.3,we deduce that for{t >τ:τ∈R andω∈Ω}there existsK={K(τ,ω)={u:‖∆u‖2≤η}}∈D.

Hence,the continuous cocycleΦhas a closed random absorbing set{A(ω)}ω∈ΩinD.By Lemma 4.1 and Lemma 4.3,the continuous cocycleΦisD-random asymptotically compact in R2.Then the existence of a uniqueD- random attractor forΦfollows from Lemma 2.1 immediately.